早在1959年,著名物理学家Feynman预言微小型系统将展现出广阔的发展空间[1],LIU Qian等[2]在带有“十”字形和“T”字形的矩形微通道内,以氮气为气相,分别以乙醇-表面活性剂水溶液或丙酮-表面活性剂水溶液为互溶混合液相,观察到泡状流、弹状流、扰动流和分层流四种流型。WANG Yuan等[3]基于可视化观测和红外测温技术对乙醇在微通道中蒸发过程的气液相界面 (即弯液面) 的特性进行了实验研究,结果发现单位长度接触线蒸发率与微通道截面长宽比有关。苏黎世联邦理工学院Fries等[4]以罗丹明B染液、氮气为实验工质,在截面尺寸为150 μm×150 μm以及150 μm×300 μm的蛇形通道内,详细研究了流体进入弯道前后以及流经弯道时的分布状态,结果显示蛇形结构对增强传质是非常有利的。目前,许多学者对直微通道内气液两相流进行了大量的研究,然而有关小曲率蛇形微通道内两相流的报道仍然比较缺乏。
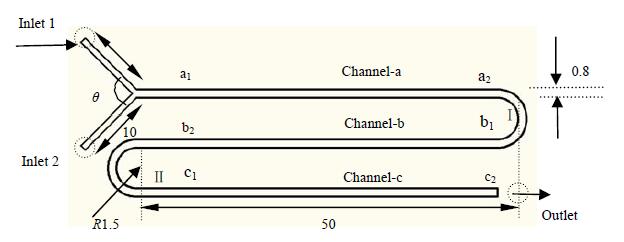
2 实验系统本试验微通道结构如图 1所示。截面采用矩形 (800 μm×100 μm),弯道I、II内径均3 mm,曲率为0.047。实验系统及过程详见参考文献[5]。
|
图 1 蛇形微通道 Fig.1 Schematic diagram of the serpentice microchannel |
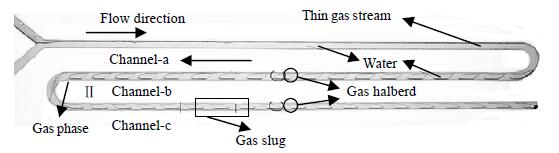
戟形弹状流:笔者在本实验中发现了一种特殊的弹状流。此时气戟和液塞交替出现,气戟的长度大于通道直径。液膜环绕在气戟周围将其与壁面隔开。该流型与以往文献中报道的气弹头部、尾部都呈规则的半球帽截然不同。
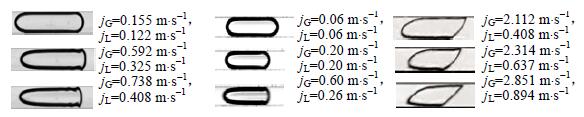
作为气液两相流动中最为重要的流型,弹状流 (有些学者也称为泰勒流) 优良的传热传质性能归结于液塞内部存在内循环[6]。但是由于通道形状、材质等因素的影响,微通道内的气弹形状并不一致。Yao等[7]以CO2、N2、去离子水为实验工质,在截面为750 μm×280 μm的Y型微通道 (PMMA材质) 内观测到气弹形状的变化过程。当气、液相表观速度都相对较低时,表面张力起主导作用,气弹头部及尾部呈现规则的半球帽,随着气相表观速度的增加,由于惯性效应的影响,其形状越来越接近子弹形,此时头部变得更加尖锐,而尾部愈加扁平。Choi等[6]在4种不同直径的T型玻璃通道内观测了水、氮气体系的两相流动,发现低速条件下气弹形状比较对称,尾部比较光滑,但在速度较高时形状发生变形,尾部起绒,这与Yao等[7]中气弹尾部产生挤压 (带有褶皱) 有着一定的区别。笔者在本次实验中也观测到类似的现象,不同的是,气弹尾部上扬,并与流动方向以一定的角度倾斜,其头部比较尖锐,就像“戟”一样呈流线型,这有利于气戟降低流动过程中的阻力,如同高速列车一样快速运行,经测定其长细比 (
|
图 2 气弹形状的变化过程 Fig.2 Profiles of gas slug shape as a function of time |
|
图 3 戟形弹状流 Fig.3 Halberd-shaped slug flow in the microchannel |
|
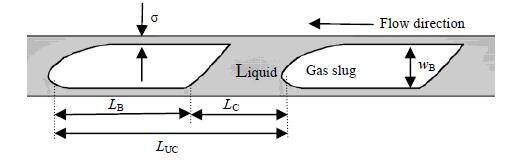
图 4 戟形弹状流模型 Fig.4 Schematic diagram of the halberd shaped slug flow |
一些学者针对泰勒流的气弹长度,提出如下模型,其中,A、B、C、D、E均为参数,如表 1所示。
| 表 1 基于模型(2)的各项参数 Table 1 Parameter values based on equation (2) |
| $\frac{{{L}_{B}}}{{{D}_{h}}}=A{{\beta }^{B}}{{(1-\beta )}^{C}}R{{e}^{D}}C{{a}^{E}}$ | (1) |
Qian等[8]以空气、水为工质,对6种不同直径的T型微通道气液两相流进行了大量的数值模拟,发现气弹长度与入口是否混合良好有着直接的关系,并指出无量纲气弹长度主要受控于相滞留率,然而受Re、Ca的影响相对较小:
| $\frac{{{L}_{B}}}{{{D}_{h}}}=1.637{{\beta }^{0.107}}{{(1-\beta )}^{-1.05}}R{{e}^{-0.075}}C{{a}^{-0.0687}}$ | (2) |
Sobieszuk[9]采用不同工质对Y型通道内的气弹长度进行统计分析,分别得到每组工况下的不同参数,最后将其平均 (各自参数见表 1),则提出:
| $\frac{{{L}_{B}}}{{{D}_{h}}}=1.302{{\beta }^{0.073}}{{(1-\beta )}^{-1.010}}R{{e}^{-0.098}}C{{a}^{-0.108}}$ | (3) |
式中,
Dang等[10]在正方形 (500 μm×500 μm) 截面的Y型微通道内考察了空气、葡萄糖溶液的两相流动,系统分析了表观流速以及液体粘度对泰勒气弹长度的影响,并提出以下经验关系式:
| $\frac{{{L}_{B}}}{{{D}_{h}}}=(1+1.71\frac{{{j}_{G}}}{{{j}_{L}}}){{\left( \frac{{{j}_{TP}}}{{{j}_{ref}}} \right)}^{-0.28}}{{\left( \frac{{{\mu }_{L}}}{{{\mu }_{ref}}} \right)}^{-0.06}}$ | (4) |
其中,参考流速
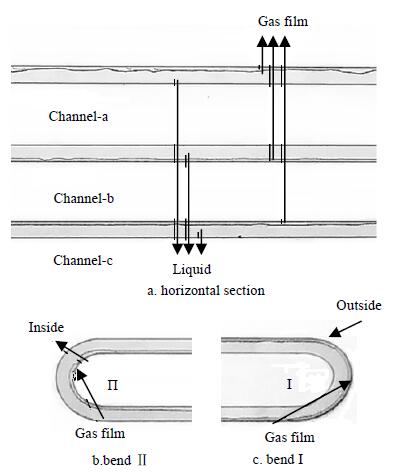
在两相流速不太高的情况下,蛇形通道内出现了附壁流,如图 5所示,此时由于惯性效应以及康达效应的影响,有一层薄薄的气流附着在壁面流动。其中a、c段气膜位于液相上方,而b段气膜则位于下方,进一步表明微尺度下重力将不占主导优势。同时,两个弯道处气液相的分布也有所差异,弯道Ⅰ处气流偏向于外侧,而弯道Ⅱ则恰好与此相反。
|
图 5 附壁流流型 Fig.5 Flow pattern of attached wall flow jG=2.538 m·s-1, jL=1.026 m·s-1 |
进一步增大气相流速,可以观测到液环流 (Tsaoulidis[11]也将其称为喉形环状流,其实质是一样的)。此时,液膜围绕在气核周围,在液相的剪切下气流颈部收缩形成像指环一样的结构,该流型在传统的常规通道中一般很难出现。另外,实验中也经常观测到气相被切断的情况,这种现象的产生有两种因素,一方面来自液相的剪切,另一方面来自圆弧诱导剪切,如图 5a,随着流动的进行,在下游处可观测到连读的多液环结构,这种现象在通道c段尤为明显,如图 5b。
在jG=4.129 m×s-1,jL=1.513 m×s-1时,可采集到典型的环状流,气相与液相经Y型口汇流后,起初气液界面不太稳定,带有一定的起伏。在后续流动中出现了一种特殊的现象,如图 6a,此时气相表观速度相对较高,气液之间存在较大的剪切,使得流动过程中气核出现拉伸最后断裂。随着流动的进行,在下游处界面才逐渐趋于稳定,如图 6b。此外,气流在流经弯道I、II时,也均偏向于内壁,液相则主要分布于外壁,这是因为液相密度相对较高,在快速流动中所受离心力比气相要大的多,故进入弯道后相分布没有水平段那样均匀,二者相界面发生了一定的偏移。王晓艳[12]对水平蛇形管环状流的换热特性进行了研究,并指出弯头处离心力以及二次流的作用使得内侧壁温要高于外侧,进一步表明弯头处相的分布发生了变化。孟勐等[13]曾对180°玻璃蛇形管内的两相流动进行了可视化实验,指出弯头内外两侧的速度场以及核化条件存在着巨大的差异。Kositanont等[14]根据甲苯难溶于水的特点,基于CFD对曲率半径0.5 mm的蛇形微通道 (内置有指引壁) 进行了数值模拟,结果发现甲苯和水在弯道处的分布位置发生了切换。以上结果均说明蛇形结构对气液两相流动具有较大的扰流作用,在实际应用中应对弯头的不同侧壁面给予注意。

|
图 6 典型环状流 Fig.6 Typical annular flow patterns in the serpentine microchannel |
空隙率作为两相流动的重要参数之一,直接决定着气液混合物的密度、黏度,同时对流型转变、两相的压降以及传热传质起到关键性的作用。因此,能否准确预测空隙率在两相流的水力计算中显得尤为重要。Beattie等[15]指出漂移流模型对环状流空隙率的预测相对要差一些。Ide等[16]以空气、水为两相工质,对矩形截面 (1.1 mm×9.9 mm) 的毛细管垂直放置以及水平放置两种情况进行了对比,综合了黏度、流速、表面张力等因素的影响,提出如下关联式:
| $\alpha ={{\{1+{{[1.86\times {{10}^{3}}E\ddot{o}_{e}^{0.75}Fr_{e}^{0.95}Re_{e}^{-1.03}C{{a}^{0.17}}(1-\beta )]}^{-1}}\beta \}}^{-1}}$ | (5) |
式中,
De是等效直径[17],定义为:
Woldesemayat等[17]指出空隙率受到质量含气率、气液相黏度、密度以及质量流速等多种参数的影响。Cioncolini等[18]以空气、氩气、R410a、水为两相工质进行了大量实验,在Woldesemayat[17]的基础上对相关参数进一步简化,认为影响空隙率的主要因素是质量含气率以及密度比,提出了一种新的环状流空隙率预测模型,并指出该模型不受工况条件以及通道尺寸的限制。
| $\alpha =\frac{p{{x}^{q}}}{1+(p-1){{x}^{q}}}$ | (6) |
其中,p、q均是密度比
| $p=-2.129+3.129{{({{\rho }_{G}}\rho _{L}^{-1})}^{-0.2186}}$ | (7) |
| $q=0.3487+0.6513{{({{\rho }_{G}}\rho _{L}^{-1})}^{0.5150}}$ | (8) |
| $x=\frac{{{M}_{\text{G}}}}{{{M}_{\text{G}}}+{{M}_{\text{L}}}}=\frac{{{j}_{G}}{{\rho }_{G}}}{{{j}_{G}}{{\rho }_{G}}+{{j}_{L}}{{\rho }_{L}}}$ | (9) |
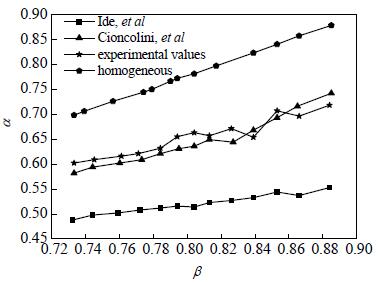
图 7显示了Ide等[16]、Cioncolini等[18]以及均相模型预测结果与当前实验结果的比较,由图可知均相模型预测值明显偏高,在实际应用中已经完全失效。Ide等[16]预测相对偏低,而Cioncolini等[18]的预测相对较好,基本与实验值相吻合。
|
图 7 环状流空隙率实验值与预测值的比较 Fig.7 Comparison of experimental and predicted values of void fraction in annular flow |
采用90°Y型入口,对蛇形微通道内空气、水两相体系进行了实验,发现了一些与直微通道不同的特殊流型。针对戟形弹状流,对气戟的长度以及与毛系数之间的关系进行了分析。基于已有空隙率模型对当前通道内环状流进行了预测。此外,气液相在流经弯道的过程中二者的分布有所区别。具体来说,有以下结论:
(1) 基于本实验,观测到的不同于直微通道的特殊流型有麦状流、戟形弹状流、附壁流。
(2) 戟形弹状流中气戟以及液塞长度并不严格一致,随着流动的进行整体上有增大的趋势。
(3) 针对蛇形微通道内气戟长度以及环状流空隙率,Qian、Cioncolini等可分别进行较好的预测。
| [1] | LFeynman R P. There is plenty of room at the bottom[J]. Journal of MEMS , 1992, 1: 60-66. DOI:10.1109/84.128057. |
| [2] | LIU Qian(刘谦), ZHANG Song-hong(张颂红), SHEN Shao-chuan(沈绍传), et al. Gas-liquid two-phase flow patterns and boundaries in a rectangular microchannel(矩形微通道内气液两相流型及其转换和实验研究)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报) , 2011, 25(6): 916-922. |
| [3] | WANG Yuan(汪元), WANG Zhen-guo(王振国). Research on interfacial characteristics of ethanol evaporation in single microchannels using visualization and infrared thermography(基于可现代观测和结外测温技术的微通道中乙醇蒸发气液相界的特性研究)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报) , 2016, 30(2): 318-324. |
| [4] | Fries D M, Waelchli S, Rohr P R. Gas-liquid two-phase flow in meandering microchannels[J]. Chemical Engineering Journal , 2008, 135: S37-S45. DOI:10.1016/j.cej.2007.07.052. |
| [5] | ZHOU Yun-long(周云龙), SUN Zhen-guo(孙振国). Gas-liquid flow characteristics in serpentine microchannels(蛇形微通道气液两相流动特性)[J]. CIESC Journal(化工学报) , 2015, 66(11): 4350-4358. |
| [6] | Choi C W, Yu D I, Kim M H. Adiabatic two-phase flow in rectangular micro-channels with different aspect ratios:PartⅡ-bubble behaviors and pressure drop in single bubble[J]. International Journal of Heat and Mass Transfer , 2010, 53(23): 5242-5249. |
| [7] | Yao Chaoqun, Zhao Yuchao, Ye Chunbo, et al. Characteristics of slug flow with inertial effects in a rectangular micro-channel[J]. Chemical Engineering Science , 2013, 95(3): 246-256. |
| [8] | Qian D, Lawal A. Numerical study on gas and liquid slugs for Taylor flow in a T-junction microchannel[J]. Chemical Engineering Science , 2006, 61(23): 7609-7625. DOI:10.1016/j.ces.2006.08.073. |
| [9] | Sobieszuk P, Cygański P, Pohorecki R. Bubble lengths in the gas-liquid Taylor flow in microchannels[J]. Chemical Engineering Research and Design , 2010, 88(3): 263-269. DOI:10.1016/j.cherd.2009.07.007. |
| [10] | Dang Minhui, Yue Jun, Chen Guangwen, et al. Formation characteristics of Taylor bubbles in a microchannel with a converging shape mixing junction[J]. Chemical Engineering Journal , 2013, 223: 99-109. DOI:10.1016/j.cej.2013.02.108. |
| [11] | Tsaoulidis D, Dore V, Angeli P, et al. Flow patterns and pressure drop of ionic liquid-water two-phase flows in microchannels[J]. International Journal of Multiphase Flow , 2013, 54: 1-10. DOI:10.1016/j.ijmultiphaseflow.2013.02.002. |
| [12] | WANG Xiao-yan (王晓艳). Experimental research on heat transfer characteristics in horizontal serpentine tube (水平蛇形管内传热特性试验研究) [D]. Zibo (淄博): Shandong University of Technology (山东理工大学), 2011. |
| [13] | MENG Meng(孟勐), PENG Xiao-feng(彭晓峰). The heat transfer heterogeneities of bends in flow boiling of hairpin tubes(蛇形管流动沸腾弯头处传热的非均匀性)[J]. Journal of Engineering Thermophysics(工程热物理学报) , 2009, 30(3): 498-500. |
| [14] | Kositanont C, Putivisutisak S, Tagawa T, et al. Multiphase parallel flow stabilization in curved micro-channel[J]. Chemical Engineering Journal , 2014, 253: 332-340. DOI:10.1016/j.cej.2014.05.023. |
| [15] | Beattie D R H, Sugawara S. Steam-water void fraction for vertical up flow in a 73.9 mm pipe[J]. International Journal of Multiphase Flow , 1986, 12(4): 641-653. DOI:10.1016/0301-9322(86)90065-0. |
| [16] | Hideo Ide, Tohru Fukano. Experimental research on the correlations of holdup and frictional pressure drop in air-water two-phase flow in a capillary rectangular channel[J]. Experimental Thermal and Fluid Science , 2005, 29(7): 833-841. DOI:10.1016/j.expthermflusci.2005.03.010. |
| [17] | Melkamu A. Woldesemayat, Afshin J. Comparison of void fraction correlations for different flow patterns in horizontal and upward inclined pipes[J]. International Journal of Multiphase Flow , 2007, 33(44): 347-370. |
| [18] | Andrea Cioncolini, John R. Thome. Void fraction predicion in annular two-phase flow[J]. International Journal of Multiphase Flow , 2012, 43: 72-84. DOI:10.1016/j.ijmultiphaseflow.2012.03.003. |




