可再生能源资源的开发与利用是应对全球能源短缺和改善环境最为直接的方式之一,太阳能制冷为节能与环境保护提供了现实的技术手段。吸附器作为太阳能吸附式制冷系统的关键部件,其内部传热性能直接影响着系统的制冷性能。为了强化吸附器内的传热,根据吸附剂吸附/解吸吸附质的功能特点,通常会在吸附器内部采用金属翅片或改变金属翅片结构型式[1~4]来减小热阻,增加吸附器的有效传热面积。邱燕等[5]对封闭空间内纵向外翅片管结构参数对传热的影响进行了研究,认为在翅片长度一定时,翅片管单位质量散热量的最大值大多出现在翅片夹角60°左右;李飞等[6]对H型翅片椭圆管束传热及阻力特性进行了实验研究,得到了管外换热实验的关联式及阻力实验的关联式;张利等[7]对椭圆形和圆形翅片管流动与传热的性能进行了数值研究,在相同结构参数下,圆形翅片管的换热系数略大于椭圆形翅片管;陈焕新等[8]分析了壳管式吸附器的传热特性,并对吸附器的强化传热进行研究,研究结果表明:吸附器的显热主要是由于吸附剂本身的显热造成的,且吸附器的显热及系统的制冷量与翅片的个数成正比变化,当翅片个数大于12时,系统的制冷量几乎不再变化;马挺等[9]研究了高温下平直翅片管的传热与阻力特性,得到了温差对阻力系数f影响较大,辐射对Nu数影响较大;张璟等[10]对平直翅片管与波浪翅片管流动换热性能进行了比较,通过对流换热系数和流动损失的对比分析表明,波浪翅片管在空气侧换热系数和流动损失方面比平直翅片管有一定优势,且在低风速工况下,其优势较为明显。
另一方面,除了吸附器的结构形式会对固体吸附式制冷系统产生影响外,系统的供能方式也至关重要。传统的平板型吸附床固体吸附制冷系统[11, 12]直接利用太阳能加热翅片管,存在加热解吸阶段吸附器受热不均匀的问题,影响了制冷剂的解吸。宋向波等[13]设计的翅片同心管吸附器可放置于保温水箱中,利用太阳能水浴式供能加热吸附器解吸,解吸阶段吸附温度较为均匀,但其未能指出采用水浴进行加热解吸时,翅片管内制冷工质耗热量的变化关系。
目前,对竖直翅片同心管吸附器水浴式吸附制冷系统传热性能的研究[14~17]还处在不断发展的过程中,本文在前人研究的基础上对翅片同心管的传热过程进行了研究,分析了解吸过程中翅片管内制冷工质耗热量的变化,并探讨了三种不同高度的翅片同心管传质通道内温度的变异系数,可为翅片同心管吸附器水浴式吸附式制冷系统的设计与应用提供参考。
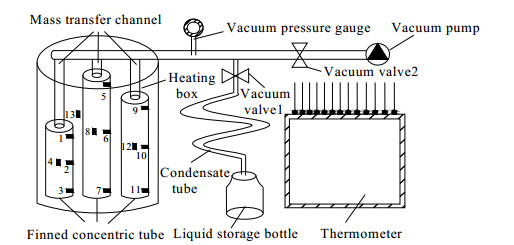
2 实验系统 2.1 实验装置及实验过程翅片同心管吸附器加热解吸过程传热性能的实验装置图如图 1所示。实验装置主要包括以下几个部分:翅片同心管吸附器、保温水箱、真空压力表、真空阀、冷凝管、储液瓶及测温仪。实验将30、40、50 cm的翅片同心管的传质通道用管道焊接起来,每个翅片同心管内填装有椰壳活性炭(吸附剂),且在三个翅片同心管的上部、中部、下部及传质通道的内部设有温度传感器,测温点从小到大(1~13)依次与测温仪相连。测温仪每间隔1 min就会收集一次实验结果,其测温范围为-40~150℃,精度为±0.1℃,分辨率为0.1℃。在实验开始之前,先启动真空泵,将整个系统抽真空至-0.075 MPa,在真空环境下,打开真空阀2,关闭真空阀1,将甲醇(制冷剂)由阀门2灌入,甲醇在真空环境下迅速气化,被翅片同心管内的椰壳活性炭吸附。灌入甲醇时,为防止空气进入,通过阀门2确保入口管道处液体甲醇的液面高度。椰壳活性炭—甲醇的主要特性参数如表 1所示。
|
图 1 实验装置图 Fig.1 Schematic diagram of the experimental setup |
| 表 1 椰壳活性炭—甲醇的主要特性参数 Table 1 Characteristics of the coconut shell activated carbon -methanol system |
加热解吸过程:在保温水箱中注入定量冷水,关闭真空阀2,打开电加热器加热保温水箱里的冷水。吸附器从水浴中吸热升温,达到解吸起始温度后开始解吸,打开真空阀门1,吸附器中解吸出的甲醇蒸气在冷凝管的作用下冷凝成液态甲醇。冷凝的甲醇流入用于度量的储液瓶。
通过电加热器对三个翅片同心管吸附器进行水浴加热,研究30、40、50 cm三种不同高度的翅片同心管内部传热过程及传质通道内的温度变化。对于翅片同心管吸附器内的传质通道来说,其所获得的热量主要由翅片管吸附器的散热及椰壳活性炭的脱附热两部分以复合换热的方式完成的。
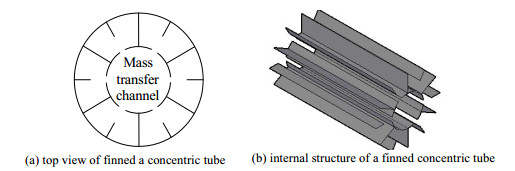
2.2 翅片同心管的结构参数翅片同心管的结构图如图 2所示,其内部共有翅片12个,大、小翅片各有6个,翅片间距为23.5 mm。该翅片同心管的外管直接吸收外部环境提供的热能,内管围成的空间作传质通道,传质通道与吸附剂以金属细丝网分隔开。翅片同心管的详细结构参数见表 2。
|
图 2 翅片同心管的结构图 Fig.2 Structure of a finned concentric tube |
| 表 2 翅片同心管的结构参数 Table 2 Structural parameters of finned concentric tubes |
在加热解吸的过程中,吸附剂的脱附热可根据Clausius-Clapeyron[18, 19]方程计算:
| $ {\left[{\frac{{{\rm{d}}({\rm{ln}}\;p)}}{{{\rm{d}}T}}} \right]_{x = {\rm{const}}}} = \frac{{h{\rm{d}}}}{{R{T^2}}} $ | (1) |
| $ x\left( {T, T{\rm{s}}} \right) = {x_0}\;{\rm{exp}}\left[{-K{{\left( {\frac{T}{{T{\rm{s}}}}-1} \right)}^n}} \right] $ | (2) |
即
| $ \frac{1}{{T{\rm{s}}}} = \frac{1}{T}\left[{{{\left( {\frac{{{\rm{ln}}\;x_{\rm{max}}-{\rm{ln}}\;x}}{K}} \right)}^{\frac{1}{n}}} + 1} \right] $ | (3) |
在吸附量一定的条件下,当温度变化范围不大时,饱和液体的压力与温度有以下关系[23, 24]:
| $ {\rm{ln}}\;p = A-\frac{C}{{T_{\rm{S}}}} $ | (4) |
式(3)代入式(4)可得:
| $ {\rm{ln}}\;p = A- \frac{C}{T}\left[{{{\left( {\frac{{{\rm{ln}}\;x_{\rm{max}}-{\rm{ln}}\;x}}{K}} \right)}^{\frac{1}{n}}} + 1} \right] $ | (5) |
| $ {\left[{\frac{{{\rm{d}}({\rm{ln}}\;p)}}{{{\rm{d}}T}}} \right]_{x = {\rm{const}}}} = \frac{{\rm{C}}}{{{T^2}}}\left[{{{\left( {\frac{{{\rm{ln}}\;x_{\rm{max}}-{\rm{ln}}\;x}}{K}} \right)}^{\frac{1}{n}}} + 1} \right] = \frac{C}{{T_{\rm{s}}T}} $ | (6) |
联立式(1)、(6)可得:
| $ h_{\rm{d}} = RC\frac{T}{{T_{\rm{s}}}} $ | (7) |
解吸过程中,对应于冷凝压力(冷凝温度Tc)的脱附热为:
| $ h_{\rm{d}} = RC\frac{T}{{T_{\rm{c}}}} $ | (8) |
所以,整个解吸过程中积分脱附热为:
| $ H_{\rm{d}} = \int\limits_{{x_1}}^{{x_{_2}}} {{h_{\rm{d}}}{m_2}{\rm{d}}x} = \int\limits_{T_{\rm{g}1}}^{T_{\rm{g}2}} {{h_{\rm{d}}}{m_2}} \frac{{\partial x}}{{\partial T}}{\rm{d}}T $ | (9) |
其中,p—翅片同心管吸附床内的压力;R—气体常数;T—吸附床内吸附剂的温度;hd、Hd—脱附热;A、C—Clausius-Clapeyron方程常数;K—D-A方程吸附参数,K是由吸附剂—制冷剂两者组合性质决定的,与温度无关,K值一般在10~50;Tc—冷凝温度;Ts—制冷剂的饱和温度;x1、x2—吸附率;Tg1、Tg2—解吸温度;m2—吸附剂的质量。表 3列出了椰壳活性炭—甲醇工质对D-A方程系数及相关的热物性公式。
| 表 3 椰壳活性炭-甲醇D-A方程系数及热物性公式 Table 3 D -A equation coefficients and thermophysical equations of the coconut shell activated carbon–methanol system |
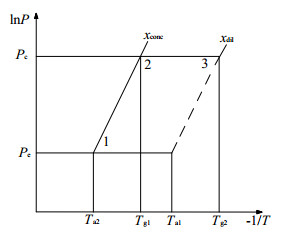
图 3是解吸过程的p-T-x图。理论上等吸附量加热过程吸附量保持不变,吸附剂和吸附质被定容加热,在解吸过程中,解吸从Tg1开始,忽略吸附器到冷凝器的压力损失,即解吸过程可简化为定压过程。
|
图 3 解吸过程的p-T-x图 Fig.3 p-T-x diagram of the desorption process |
在整个过程中,吸附器加热及解吸过程的总耗热量由四个部分组成,分别为吸附器的显热、吸附剂的显热、吸附质的显热以及脱附热,四个部分的热量关系式如下。
吸附器的显热:
| $ Q_1 = \int\limits_{{T_{{\rm{a2}}}}}^{T{}_{{\rm{g2}}}} {{c_{\rm{1}}}{\rm{(}}T{\rm{)}}{m_{\rm{1}}}} {\rm{ d}}T $ | (10) |
式中,c1(T)—吸附器的比热容;m1—吸附器的质量。
吸附剂的显热:
| $ Q_2 = \int\limits_{{T_{{\rm{a}}2}}}^{{T_{{\rm{g}}2}}} {{c_2}(T){m_2}} {\rm{d}}T $ | (11) |
式中,c2(T)—吸附剂的比热容;m2—吸附剂的质量。
需要指出的是,过程1-2中的吸附量不变,而在过程2-3中的吸附量是逐渐减小的。
吸附质的显热:
| $ {Q_3} = \int\limits_{{T_{{\rm{a}}2}}}^{{T_{{\rm{g}}1}}} {{m_{\rm{2}}}{\rm{ }}{x_{{\rm{conc}}}}{\rm{ }}c{}_{{\rm{v }}}{\rm{(}}T{\rm{) d}}T} + \int\limits_{{T_{{\rm{g}}1}}}^{{T_{_{{\rm{g}}2}}}} {{m_{\rm{2}}}c_{\rm{p (}}T{\rm{)}}x{\rm{ (}}T{\rm{,}}T_{\rm{c)}}{\rm{d}}T} $ | (12) |
通常认为吸附质在吸附剂微孔中冷凝后以液态存在,因此,cv(T)为液态制冷剂的比定容热容;cp(T)为液态制冷剂的比定压热容。在过程2-3中,吸附质的解吸所需的解吸热即是解吸过程中的脱附热Hd,而在过程1-2中吸附量不变,即:
| $ {x_{{\rm{conc}}}} = x({T_{{\rm{a2}}}},{T_{\rm{c}}}) = x({T_{{\rm{g1}}}},{T_{\rm{c}}}) $ | (13) |
所以,吸附器加热及解吸过程中总耗热量为:
| $ {Q_{1 - 2 - 3}} = {Q_1} + {Q_2} + {Q_3} + {H_{\rm{d}}} $ | (14) |
而解吸过程中传质通道内获得的热量应该等于吸附器加热及解吸过程中总耗热量Q1-2-3,且总热量以复合换热的方式传递到传质通道中,即:
| $ {Q_{1 - 2 - 3}} = A'\varepsilon {\rm{\sigma }}\left( {{T_{\rm{w}}}^4 - {T_{\rm{f}}}^4} \right) + h'A'\left( {{T_{\rm{w}}} - {T_{\rm{f}}}} \right) $ | (15) |
其中,A’为收到辐射的面积;ε为发射率;σ为黑体辐射常数;h’为复合换热表面传热系数;Tw为吸附剂表面温度;Tf为传质通道内温度。
3.3 温度的变异系数变异系数(C.V)可以反映不同高度的翅片管传质通道内温度的离散程度,变异系数可以消除单位和(或)平均数不同对两个或多个测量值变异程度比较的影响。变异系数的计算公式定义为:
| $ C.V = \frac{S}{{\bar x}} \times 100{\rm{\% }} $ | (16) |
式中,S为标准差;x为平均数。
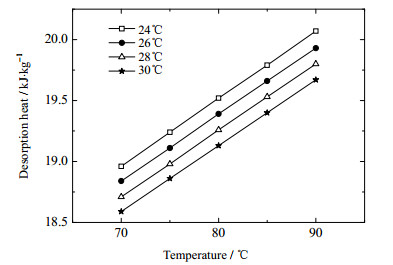
4 分析与讨论 4.1 加热解吸过程中耗热量的变化在加热解吸的过程中,吸附器处于封闭状态不断吸收热量,吸附器内的吸附剂和吸附质被定容加热,在未达到解吸温度之前,吸附质的解吸还需要解吸热(脱附热)。图 4反应的是不同冷凝温度下吸附质脱附热随吸附剂温度的变化。从图中可以看出,吸附质的脱附热随着吸附剂温度的升高而不断增大,且在相同的吸附剂温度下,冷凝温度越低,吸附质的脱附热越大。由于冷凝温度的变化会导致冷凝压力的变化,从而影响了吸附质的脱附热。
|
图 4 吸附质脱附热随吸附剂温度的变化 Fig.4 Profiles of desorption heat of adsorbate as a function of adsorbent temperature |
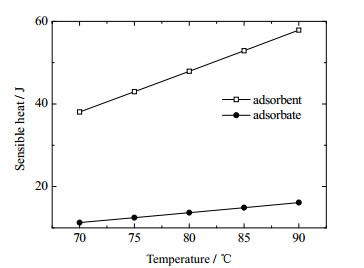
图 5为相同吸附剂质量下翅片同心管吸附器解吸过程显热量的变化图。由图可知,吸附剂和吸附质的显热量随吸附剂温度的升高而不断增大,且在相同温度下,吸附剂的显热量远大于吸附质的显热量,这是由于吸附剂不可能完全吸附制冷剂所导致的。
|
图 5 翅片同心管吸附器解吸过程显热量的变化 Fig.5 Profiles of sensible heat of the finned concentric tube adsorber during desorption processes |
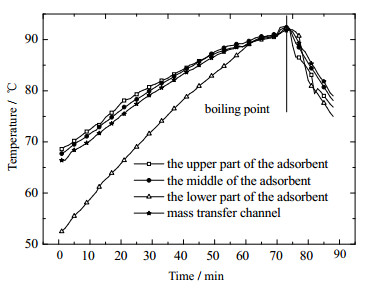
图 6、图 7、图 8分别为30、40、50 cm翅片同心管内部的温度变化图。从图中可以看出,无论是在沸点前后,翅片同心管内的传质通道的温度都与吸附剂中部的温度最为接近,两者的温度相差0.1~1.5℃;而翅片同心管的底部由于直接与保温水箱的底部接触,导致了翅片同心管下部的温度刚开始比较低,经过近1 h后,吸附剂下部的温度才恢复正常。
|
图 6 30 cm翅片同心管内部的温度变化 Fig.6 Internal temperature profiles of the 30 cm-high finned concentric tube |
|
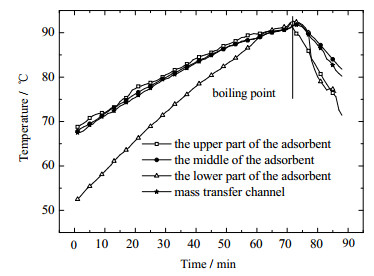
图 7 40 cm翅片同心管内部的温度变化 Fig.7 Internal temperature profiles of the 40 cm-high finned concentric tube |
|
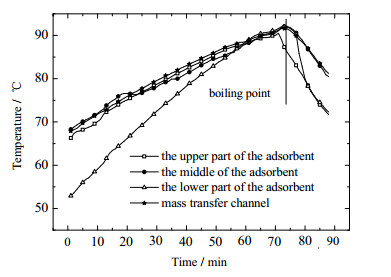
图 8 50 cm翅片同心管内部的温度变化 Fig.8 Internal temperature profiles of the 50 cm-high finned concentric tube |
对比30、40、50 cm翅片同心管内部的温度变化图后,可以发现,相比30、50 cm翅片同心管,40 cm翅片同心管内的传质通道温度一直与吸附剂中部温度的吻合程度较高;达到沸点之后,在自然冷却的过程中,相比传质通道和吸附剂中部的温度,吸附剂上部和下部的温度下降的速度相对较快。
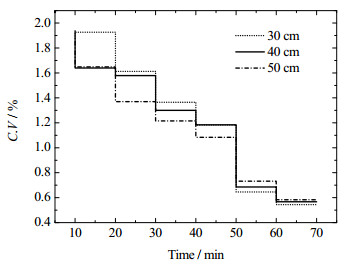
4.3 三种不同高度的翅片同心管传质通道内温度的变异系数三种不同高度的翅片管传质通道内温度的离散程度图如图 9所示。由图可知,三种不同高度的翅片同心管传质通道内温度的变异系数随着时间的变化逐渐降低,也就是说,随着水温的不断升高,翅片同心管传质通道内温度的离散程度越来越小,在升高至93℃左右时(水已经沸腾),气体传质通道内温度的变异系数达到最小,此时,传质通道内的温度最为稳定。对比30、40、50 cm翅片同心管传质通道内温度的变异系数可以知道,在前50 min内,30 cm翅片同心管传质通道内温度的变异系数较大,50 cm翅片同心管传质通道内温度的变异系数则相对较小;在后20 min内,两者传质通道内温度的变异系数与前50 min截然相反,而40 cm翅片同心管传质通道内温度的变异系数则一直在两者的中间波动,其传质通道内温度的变异系数相对较于稳定。
|
图 9 不同高度的翅片管传质通道内温度的离散程度 Fig.9 Degree of dispersion of temperature in mass transfer channel of fin tubes with different heights |
本文对30、40、50 cm三种高度不同的翅片同心管吸附器内部的传热过程进行了研究,得出了以下结论:(1)吸附质的脱附热随着吸附剂温度的升高而增大,且在相同的吸附剂温度下,冷凝温度越低,吸附质的脱附热越大;(2)吸附剂和吸附质的显热量随吸附剂温度的升高而增大,且在相同温度下,吸附剂的显热量约是吸附质的3倍;(3)翅片同心管内的传质通道的温度都与吸附剂中部的温度最为接近,两者的温度相差0.1~1.5℃,与30、50 cm翅片同心管相比,40 cm翅片同心管内的传质通道温度与吸附剂中部温度的吻合程度较高;(4)与30、50 cm翅片同心管吸附器相比,40 cm翅片同心管吸附器传质通道内温度的变异系数相对较于稳定。
符号说明:
| A’ | —接收到辐射的面积,m2 | R | —气体常数 |
| A、C | —Clausius-Clapeyron方程常数 | S | —标准差 |
| c1 | —吸附器的比热容,kJ·(kg·K)-1 | T | —吸附器内吸附剂的温度,℃ |
| c2 | —吸附剂的比热容,kJ·(kg·K)-1 | Tc | —冷凝温度,℃ |
| cp | —液态制冷剂的比定压热容,kJ·(kg·K)-1 | Tf | —传质通道内温度,℃ |
| cv | —液态制冷剂的比定容热容,kJ·(kg·K)-1 | Tg1 | —开始解吸温度,℃ |
| hd、Hd | —脱附热 | Tg2 | —解吸温度,℃ |
| h’ | —复合换热表面传热系数,W·(m2·K)-1 | Ts | —制冷剂的饱和温度,℃ |
| K | — D-A方程吸附参数 | Tw | —吸附剂表面温度,℃ |
| k | —吸附特征参数 | x | —吸附率,kg·kg-1 |
| m1 | —吸附器的质量,kg | x | —平均数 |
| m2 | —吸附剂的质量,kg | ε | —发射率 |
| p | —翅片同心管吸附床内的压力,MPa | σ | —黑体辐射常数 |
| [1] | MA You-fu(马有福), YUAN Yi-chao(袁益超), LIU Yu-zheng(刘聿拯), et al. Experimental studies on the effects of transverse pitch on heat transfer and flow resistance characteristics of serrated spiral finned tube banks(横向节距对锯齿螺旋翅片换热管特性影响的实验研究)[J]. Proceedings of the CSEE(中国电机工程学报) , 2011, 31(8): 67-72. |
| [2] | He Y L, Chu P, Tao W Q, et al. Analysis of heat transfer and pressure drop for fin-and-tube heat exchangers with rectangular winglet-type vortex generators[J]. Applied Thermal Engineering , 2013, 61(2): 770-783. DOI:10.1016/j.applthermaleng.2012.02.040. |
| [3] | WEN Jian(文键), YANG Hui-zhu(杨辉著), XUE Yu-lan(薛玉兰), et al. Experimental investigation on heat transfer performance of heat exchanger with ladder-type fold baffles(旋梯式螺旋折流板换热器换热性能的实验研究)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报) , 2015, 29(4): 795-801. |
| [4] | ZHANG Li(张丽), TIAN Mi-mi(田密密), WU Jian-hua(吴剑华). Heat transfer performance of the shell side of double-pipe heat exchanger enhanced with helical fins(螺旋片强化的套管式换热器壳侧传热特性)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报) , 2011, 25(1): 24-29. |
| [5] | QIU Yan(邱燕), TIAN Mao-cheng(田茂诚), LENG Xue-li(冷学礼). Heat transfer characteristic of longitudinal externally-finned tube in closed space(封闭空间内纵向外翅片管结构参数对传热的影响)[J]. CIESC Journal(化工学报) , 2013, 64(7): 2405-2410. |
| [6] | LI Fei(李飞), SHI Yue-tao(史月涛), SUN Feng-zhong(孙奉仲), et al. Experimental research on heat transfer and resistance characteristics of H-type finned elliptical tubes(H型翅片椭圆管束传热及阻力特性的试验研究)[J]. Proceedings of the CSEE(中国电机工程学报) , 2014, 34(14): 2261-2266. |
| [7] | ZHANG Li(张利), YANG Kun(杨昆), LIU Wei(刘伟). Numerical study on flow and heat transfer in an elliptical and circular finned tube(椭圆形和圆形翅片管流动与传热的数值研究)[J]. Journal of Engineering Thermophysics(工程热物理学报) , 2009, 30(9): 1571-1574. |
| [8] | CHEN Huan-xin(陈焕新), WEI Li(魏莉), ZHANG Chuo(张绰), et al. Heat transfer characteristics and enhancement of shell and tube adsorbent beds(壳管式吸附床传热特性及其强化传热研究)[J]. Journal of Hua Zhong University of Science and Technology(华中科技大学学报) , 2012, 40(10): 44-48. |
| [9] | MA Ting(马挺), ZENG Min(曾敏), XIE Gong-nan(谢公南), et al. Numerical study on heat transfer and pressure drop characteristics of plain-finned tube under high temperature(高温下平直翅片管传热与阻力特性的数值研究)[J]. Journal of Engineering Thermophysics(工程热物理学报) , 2010, 31(9): 1571-1574. |
| [10] | ZHANG Jing(张璟), LI Yan-jun(李宴君), WEN Juan(温娟), et al. Flow and heat transfer characteristics comparison between flat wave-fin tube and corrugated-fin flat tube(平直翅片管与波浪翅片管流动换热性能比较)[J]. Journal of Engineering Thermophysics(工程热物理学报) , 2011, 32(8): 1368-1370. |
| [11] | 李明. 基于太阳能利用的固体吸附式制冷循环研究[D]. 上海上海交通大学, 1999. LI Ming. Study on solid adsorption refrigeration cycle based on solar energy utilization [D]. Shanghai Shanghai Jiao Tong University, 1999. http://d.wanfangdata.com.cn/Periodical_ynsfdxxb200702009.aspx |
| [12] | Leite A P F, Daguenet M. Performance of a new solid adsorption ice maker with solar energy regeneration[J]. Energy Conversion and Management , 2000, 41(15): 1625-1647. DOI:10.1016/S0196-8904(00)00011-X. |
| [13] | 宋向波. 太阳能水浴式固体吸附制冷系统设计及性能特性研究[D]昆明: 云南师范大学, 2016. SONG Xiang-bo. Design and performance characteristics of solar water bath solid adsorption refrigeration system [D] Kunming : Yunnan Normal University, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10681-1016746702.htm |
| [14] | FAN Jie-qing(范介清), LUO Bin(罗斌), WANG Liu-ling(王六玲), et al. Study on the performance of the integral finned tube heat and mass transfer enhanced solar adsorption cooling system(翅片管整体传热传质强化的太阳能吸附式制冷系统性能研究)[J]. Acta Energiae Solaris Sinica(太阳能学报) , 2014, 35(9): 1663-1669. |
| [15] | Ji X, Li M, Fan J Q, et al. Structure optimization and performance experiments of a solar-powered finned-tube adsorption refrigeration system[J]. Applied Energy , 2014, 113: 1293-1300. DOI:10.1016/j.apenergy.2013.08.088. |
| [16] | Thimmaiah P C, SharafianA , Huttema W, et al. Performance of finned tubes used in low-pressure capillary-assisted evaporator of adsorption cooling system[J]. Applied Thermal Engineering , 2016, 106: 371-380. DOI:10.1016/j.applthermaleng.2016.06.038. |
| [17] | Louajari M, Mimet A, Ouammi A. Study of the effect of finned tube adsorber on the performance of solar driven adsorption cooling machine using activated carbon-ammonia pair[J]. Applied Energy , 2011, 88(3): 690-698. DOI:10.1016/j.apenergy.2010.08.032. |
| [18] | Saw V K, Ahmad I, Mandal A, et al. Methane hydrate formation and dissociation in synthetic seawater[J]. Journal of Natural Gas Chemistry , 2012, 21(6): 625-632. DOI:10.1016/S1003-9953(11)60411-8. |
| [19] | XU Sheng-zhi(徐圣知), WANG Li-wei(王丽伟), WANG Ru-zhu(王如竹). Thermodynamic analysis of mass and heat recovery adsorption refrigeration cycles and scheme selection(回质回热吸附式制冷循环的热力学分析与方案优选)[J]. CIESC Journal(化工学报) , 2016, 67(6): 2202-2210. |
| [20] | Di J, Wu J Y, Xia Z Z, et al. Theoretical and experimental study on characteristics of a novel silica gel-water chiller under the conditions of variable heat source temperature[J]. International Journal of Refrigeration , 2007, 30(3): 515-526. DOI:10.1016/j.ijrefrig.2006.07.022. |
| [21] | Critoph R E. Performance limitations of adsorption cycles for solar cooling[J]. Soar Energy , 1988, 41(1): 21-31. DOI:10.1016/0038-092X(88)90111-9. |
| [22] | Tamainot-Telto Z, Critoph R E. Adsorption refrigerator using monolithic carbon-ammonia pair[J]. International Journal of Refrigeration , 1997, 20(2): 146-155. |
| [23] | Ramirez-Pastor A J, Bulnes F. Different heat of adsorption in the presence of an order-disorder phase transition[J]. Physica A , 2000, 283: 198-203. DOI:10.1016/S0378-4371(00)00152-7. |
| [24] | TENG Yi(滕毅), WANG Ru-zhu(王如竹), WU Jing-yi(吴静怡), et al. Theoretical analysis of adsorption refrigeration/heat pump cycle(对吸附式制冷/热泵循环的理论分析)[J]. Acta Energiae Solaris Sinica(太阳能学报) , 1997, 18(1): 22-30. |




