2. 浙江大学衢州研究院, 浙江 衢州 324000
2. Institute of Zhejiang University-Quzhou, Quzhou 324000, China
气固鼓泡流化床是化学工业中常见的流化床型式,例如催化裂化和甲醇制烯烃装置中的汽提器和部分立式输送管路均在鼓泡流态化下操作[1-2]。气固鼓泡流化床中存在乳相和气泡相,乳相中的气体由颗粒之间的空隙通过颗粒床层,气泡相中的气体则以气泡的形式通过颗粒床层,因此,气泡的生成、发展和运动是影响鼓泡流化床反应器特性的关键因素[3]。大尺寸气泡的存在可能导致部分气相无法有效地与固相接触、加剧颗粒的返混和夹带等问题,从而使反应器内的化学反应难以达到预期的转化率和选择性[4]。为了提高鼓泡流化床的流态化性能,可以通过设置内构件来抑制气泡生长、破碎大尺寸气泡、强化气固混合等[5]。内构件技术作为一个简单、经济的改善流态化性能的手段,目前已成功应用于丁烯氧化脱氢、苯氧化法制顺酐等工业过程中[3]。
为了研究内构件对鼓泡流化床内气固流动的影响,许多学者已成功借助计算流体力学(CFD)方法获得了实验难以测量的微观流动状况,例如气泡的尺寸、形状和频率及气固混合特性等[6-11]。石孝刚等[6]使用双流体模型(TFM) 研究带有倾斜挡板的二维鼓泡流化床内的气固流动特性,结果表明,挡板影响区域内气泡的平均尺寸降低、气泡数量增加;且气速越高,挡板的作用越强。Gao等[7]使用TFM模型计算对比了带有V型挡板和不带内构件的FCC汽提器中的气固混合特性,结果表明,V型挡板汽提器可以有效提高气固混合效率、降低催化剂返混,从而提高汽提器的汽提效率。Zhu等[10]利用计算颗粒流体力学(CPFD)方法对化学链燃烧过程中的鼓泡流化床进行模拟,探究了挡板的数量、开孔率等参数对鼓泡流化床中气泡尺寸、压力梯度、颗粒分布等方面的影响,结果表明,挡板显著改善了流化床中的气固接触。Yang等[11]使用CPFD方法对二维单旋导向挡板鼓泡流化床进行模拟,探究单旋导向挡板对床内固含率、压差波动、气泡行为的影响,提出了二维单旋挡板在较高表观气速下破碎气泡的机制。
CPFD是一种结合欧拉双流体模型与拉格朗日离散模型各自优点的计算流体力学方法,通过引入“计算颗粒”这一概念,将多个真实颗粒打包进行计算,在保证计算精度的同时极大地降低了计算资源和成本。目前已有许多学者采用CPFD方法研究无内构件鼓泡流化床内的气固流动特性[12-15],但针对三维单旋挡板鼓泡流化床的研究相对较少。本研究使用CPFD方法耦合Igci曳力模型,对三维单旋导向挡板鼓泡流化床内的气固流动进行模拟,首先将轴向和径向时均固含率分布模拟结果与实验数据进行对比来验证计算方法的可靠性,随后考察有、无内构件时鼓泡流化床内的气泡平均当量直径分布和气体停留时间分布。
2 计算方法 2.1 CPFD数学模型使用CPFD Barracuda软件对单旋导向挡板鼓泡流化床进行模拟。在CPFD中,气相被视为连续相,通过Naiver-Stokes方程来描述,颗粒被视为离散相,通过拉格朗日框架下的MP-PIC方法描述。引入“计算颗粒”这一概念,将多个具有同样物化性质和运动状态的真实颗粒打包,可大幅度降低计算成本。关于CPFD方法的详细描述及相关表达式见文献[16]。
2.2 气固曳力模型气固曳力是气固两相流中最重要的作用力之一,因此,选择合适的曳力模型是准确模拟和描述鼓泡流化床内两相流动的关键。通常有两种类型曳力模型被应用于模拟气固两相流:均匀模型(homogeneous drag model) 和非均匀模型(heterogeneous drag model)。前者以Wen & Yu模型[17]和Gidaspow模型[18]为代表,在应用中往往会高估曳力从而导致床层过度膨胀。为了克服均匀曳力模型的缺点,多种非均匀曳力模型被提出,例如经典的过滤曳力模型和EMMS曳力模型。过滤曳力模型[19]是通过细网格模拟捕捉小尺度的非均匀结构,并在时空尺度上平均化,从而建立曳力系数与气固滑移速度、局部固含率等参数的本构关联式。EMMS曳力模型[20]采用多尺度分析方法并运用能量最小原理,建立气固曳力与鼓泡流化床整体、局部参数之间的关系。
本研究采用Igci曳力模型即Igci等[21]基于颗粒动理学和双流体模型的细网格模拟推导出的过滤曳力模型对单旋导向挡板鼓泡流化床进行模拟计算,并通过实验数据对模拟结果进行验证。以下是Igci曳力模型的数学表达式。
在CPFD中,单颗粒的曳力通过式(1)和(2)描述:
| $\mathit{\boldsymbol{F}} = {m_{\rm{p}}}D\left( {{\mathit{\boldsymbol{u}}_{\rm{g}}} - {\mathit{\boldsymbol{u}}_{\rm{p}}}} \right)$ | (1) |
| $D = \frac{3}{4}{C_{\rm{d}}}\frac{{{\rho _{\rm{g}}}\left| {{\mathit{\boldsymbol{u}}_{\rm{g}}} - {\mathit{\boldsymbol{u}}_{\rm{p}}}} \right|}}{{{\rho _{\rm{p}}}{d_{\rm{p}}}}}$ | (2) |
式中:
| ${C_d} = \left\{ {\begin{array}{*{20}{l}} {\frac{{24}}{{Re}}\varphi _{\rm{g}}^{ - 2.65}}&{\quad Re < 0.5} \\ {\frac{{24}}{{Re}}\varphi _{\rm{g}}^{ - 2.65}\left( {1 + 0.15R{e^{0.687}}} \right)}&{\quad 0.5 \leqslant Re \leqslant 1\;000} \\ {0.44\varphi _{\rm{g}}^{ - 2.65}}&{\quad Re > 1\;000} \end{array}} \right.$ | (3) |
式中:φg为气相体积分数,Re为雷诺数。在CPFD Barracuda软件中,Re通过式(4)描述:
| $Re = \frac{{\left| {{\mathit{\boldsymbol{u}}_{\rm{g}}} - {\mathit{\boldsymbol{u}}_{\rm{p}}}} \right|{\rho _{\rm{g}}}{d_{\rm{p}}}}}{{{\mu _{\rm{g}}}}}$ | (4) |
Igci曳力模型在Wen & Yu模型基础上通过非均匀系数HIgci进行修正,如式(5)和(6)所示:
| ${D_{{\rm{Igci}}}} = {H_{{\rm{Igci}}}}{D_{{\rm{Wen}}\& {\rm{Yu}}}}$ | (5) |
| ${H_{{\rm{Igci}}}} = 1 - \frac{{{{\left( {\Delta _{{\rm{filter}}}^*} \right)}^{1.6}}}}{{{{\left( {\Delta _{{\rm{filter}}}^*} \right)}^{1.6}} + 0.4}}{H_2}_{\rm{D}} \cdot \xi $ | (6) |
式中:DIgci和DWen & Yu分别表示经Igci和Wen & Yu曳力模型计算得到的式(2)中的曳力方程;
| $\Delta _{{\rm{filter}}}^* = \frac{{g{\Delta _{{\rm{filter}}}}}}{{u_{\rm{t}}^2}}$ | (7) |
| ${u_{\rm{t}}} = \frac{{gd_{\rm{p}}^2\left( {{\rho _{\rm{p}}} - {\rho _{\rm{g}}}} \right)}}{{18{\mu _{\rm{g}}}}}$ | (8) |
| $\xi = \left\{ \begin{gathered} \varphi _{\rm{p}}^{0.24}\left( {1.48 + {e^{ - 18{\varphi _{\rm{p}}}}}} \right)\quad \quad \quad {\varphi _{\rm{p}}} < 0.18 \\ 1\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad {\varphi _{\rm{p}}} \geqslant 0.18 \\ \end{gathered} \right.$ | (9) |
| ${H_{\rm{2D}}} = \left\{ {\begin{array}{*{20}{l}} {2.7\varphi _{\rm{p}}^{0.234}}&{{{\varphi _{\rm{p}}}} < 0.012} \\ { - 0.019\varphi _{\rm{p}}^{ - 0.455} + 0.963}&{0.012 \leqslant {{\varphi _{\rm{p}}}} < 0.014} \\ {0.868{e^{ - 0.38{{\varphi _{\rm{p}}}}}} - 0.176{e^{^{ - 119.2{{\varphi _{\rm{p}}}}}}}}&{0.014 \leqslant {{\varphi _{\rm{p}}}} < 0.250} \\ { - 4.59 \times {{10}^{ - 5}}{e^{19.75{{\varphi _{\rm{p}}}}}} + 0.852{e^{^{ - 0.268{{\varphi _{\rm{p}}}}}}}}&{0.250 \leqslant {{\varphi _{\rm{p}}}} < 0.455} \\ {\left( {{{\varphi _{\rm{p}}}} - 0.59} \right)\left( { - 1\;501\varphi _{\rm{p}}^3 + 2\;203\varphi _{\rm{p}}^2 - 1\;054{{\varphi _{\rm{p}}}} + 162} \right)}&{0.455 \leqslant {{\varphi _{\rm{p}}}} < 0.590} \\ 0&{{{\varphi _{\rm{p}}}} \geqslant 0.590} \end{array}} \right.$ | (10) |
式中:Δfilter为过滤尺寸,m;ut为颗粒终端速度,m·s-1;μg为气体黏度,Pa·s;φp为固相体积分数,亦称为固含率。
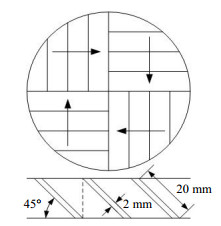
2.3 模拟设置模拟对象为文献中的一套带有两层单旋导向挡板的三维冷模实验装置[9, 22],其结构如图 1所示。该装置中流态化段主体部分为ϕ140 mm×1 000 mm的有机玻璃圆筒,底部采用金属烧结板作为气体分布器,内置两层单旋导向挡板,其中叶片宽20 mm、叶片倾角45°、叶片间距14 mm、挡板整体厚度14 mm,图 1中箭头表示倾斜方向。
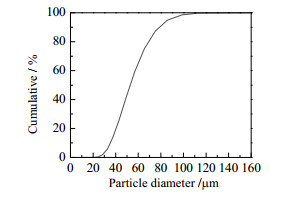
实验所采用的颗粒为玻璃微珠,颗粒密度为2 450 kg·m-3,堆积密度为1 395 kg·m-3,平均粒径为53 μm。该玻璃微珠属于A类颗粒,其粒径分布如图 2所示。在模拟计算中采用此真实粒径分布。
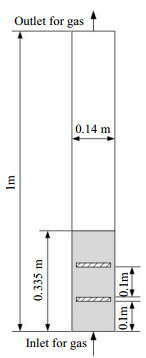
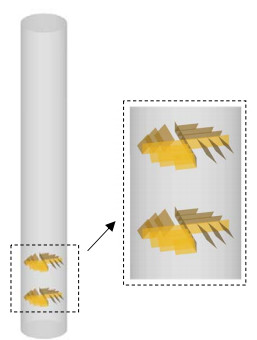
模拟过程中所设置的参数见表 1,流态化介质选择空气,计算中空气由底部均匀进入鼓泡流化床(见图 3)。流化床底部为速度边界条件,顶部为压力边界条件。在CPFD中使用挡板组件(Baffles)对两层单旋导向挡板内构件进行建模,如图 4所示。在三维模拟计算中,时间步长初始为5×10-4 s,随后由程序自动调整以保证收敛条件判断数介于0.8与1.5之间。总计算时间为70 s,取最后20 s进行时均处理和分析,从而得到计算结果。
|
|
表 1 模拟参数 Table 1 Simulation parameters |
|
图 3 单旋导向挡板三维鼓泡流化床模拟示意图 Fig.3 Schematic diagram of the simulated 3D bubbling fluidized bed with louver baffles |
|
图 4 CPFD挡板设置示意图 Fig.4 Schematic diagram of baffle arrangement in CPFD |
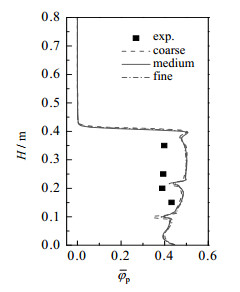
为了考察网格分辨率和计算颗粒数对模拟结果的影响,采用三种不同精度的网格和计算颗粒数对两层单旋导向挡板鼓泡流化床进行模拟,表 2列出了所使用的三种精度的网格数和计算颗粒数配置。图 5为轴向截面时均固含率
|
|
表 2 网格和计算颗粒数 Table 2 Parameters of grids and particle clouds |
|
图 5 不同分辨率下轴向时均固含率模拟值与实验值对比 Fig.5 Comparison of simulated value and experimental data of time-averaged axial solid volume fraction at different resolutions |
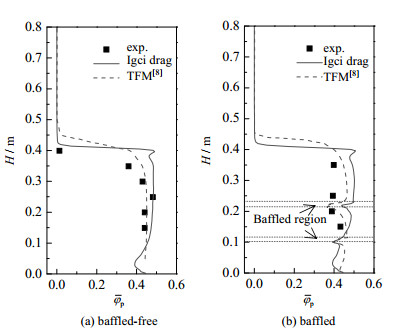
采用Igci曳力模型分别对有、无两层单旋导向挡板鼓泡流化床进行模拟,图 6为轴向
|
图 6 有、无两层单旋导向挡板时鼓泡流化床轴向时均固含率模拟值与实验数据对比 Fig.6 Comparison of simulated value and experimental data of time-averaged axial solid volume fraction of the bubbling fluidized beds with/without two louver baffles |
|
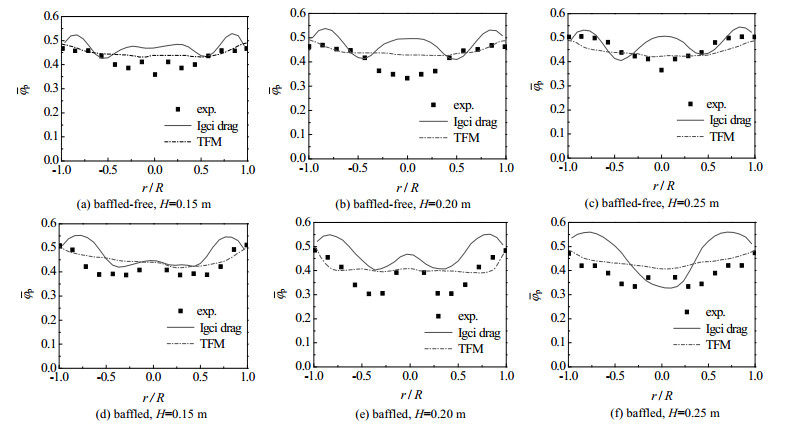
图 7 有、无两层单旋导向挡板鼓泡流化床径向时均固含率模拟值与实验数据对比 Fig.7 Comparison of simulated value and experimental data of time-averaged radial solid volume fraction of the bubbling fluidized beds with/without two louver baffles |
使用Bakshi等[23]提出的多相流三维检测和追踪算法(MS3DATA) 对有、无单旋导向挡板时的鼓泡流化床内的气泡进行统计和分析。在模拟计算过程中,每0.01 s记录1次床内的瞬时流场状态,取50~70 s内的2 000帧数据作为样本追踪和统计气泡,设置气泡相的阈值为0.7 (气相体积分数)。采用Darton[24]和Rowe等[25]的关联式来预测鼓泡流化床内的气泡当量直径,其表达式分别为式(11)和(12),使用式(13)[26]来计算最大气泡直径。
| ${D_{\rm{b}}} = 0.54{\left( {{u_{\rm{g}}} - {u_{{\rm{mf}}}}} \right)^{2/5}}{\left( {H{\rm{ }} + {\rm{ }}{h_0}} \right)^{4/5}}{g^{ - 1/5}}$ | (11) |
| ${D_{\rm{b}}} = {\left( {{u_{\rm{g}}} - {u_{{\rm{mf}}}}} \right)^{1/2}}{\left( {H{\rm{ }} + {\rm{ }}{h_0}} \right)^{3/4}}{g^{ - 1/4}}$ | (12) |
| ${D_{{\rm{bm}}}} = 0.652{\left[ {{A_{\rm{t}}}\left( {{u_{\rm{g}}} - {u_{{\rm{mf}}}}} \right)} \right]^{2/5}}$ | (13) |
式中:Db为气泡平均当量直径,m;ug为表观气速,m·s-1;umf为起始流化速度,m·s-1,实验中所用的玻璃微珠的起始流化速度为0.005 1m·s-1;h0为常数,取h0 = 0.03 m[7];g为重力加速度,m·s-2;Dbm为最大气泡直径,m;At为气体入口截面积,m2。
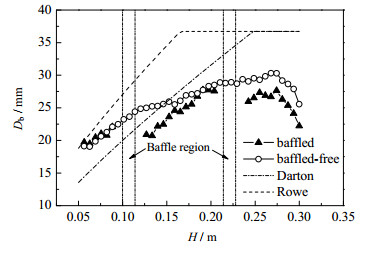
图 8为有、无两层单旋导向挡板时鼓泡流化床内的Db随H统计分析结果。由图可见,有单旋导向挡板时的床内气泡特征不同于无导向挡板即空筒鼓泡流化床时的气泡特征。在空筒鼓泡流化床中,随H增大Db不断增大,且未出现气泡破碎现象;而在有单旋导向挡板鼓泡流化床中,第一层挡板下方的Db大小以及变化规律与空筒鼓泡流化床相似,但经过第一层挡板时,Db变小,这说明单旋导向挡板对气泡有一定破碎作用;经过第一层挡板后,气泡又重新开始聚并,Db逐渐增大;同理,经过第二层挡板时,Db再次变小。由图还可见,大部分床高处的气泡尺寸模拟结果与Darton关联式预测结果趋势相吻合,但在流化床上界面附近,有、无两层单旋导向挡板时鼓泡流化床内的Db均出现明显变小的趋势,这是由于MS3DATA算法基于体积计算气泡当量直径,而在此区域气泡已经开始穿越流化床界面,从而导致该算法统计的气泡体积偏小。图 8表明,有挡板的鼓泡流化床内Db小于空筒鼓泡流化床的,但减小程度相对有限,这可能是由于实验中所使用的单旋导向挡板叶片数量较少、开孔率大,从而起到的气固搅拌作用相对较弱,因此,在实际应用中需要进一步对此单旋导向挡板的开孔率、叶片数量和角度等进行优化。
|
图 8 气泡平均当量直径沿床高分布图 Fig.8 Axial distribution of average equivalent bubble diameters |
使用脉冲示踪法研究有、无两层单旋导向挡板时鼓泡流化床内气体返混现象和气体停留时间分布(RTD)。计算中用空气作为示踪剂,在第20 s至20.01 s内注入示踪剂,令其流速与主风流速保持一致。在此时间间隔内,设置主风流速为0,以保证示踪剂的注入不会对床内的气固流动状态产生影响。记录每个时间步时流化床出口处示踪剂浓度,每200个时间步内对示踪剂浓度取一次平均,得到有、无两层单旋导向挡板时鼓泡流化床内的气体停留时间分布曲线,如图 9所示,图中θ为对比时间(无因次),E(θ)为停留时间分布密度函数。

|
图 9 气体停留时间分布图 Fig.9 Profiles of gas residence time distribution |
由图 9可见,有、无挡板时鼓泡流化床内的气体停留时间分布趋势基本相同,有单旋导向挡板鼓泡流化床内的停留时间分布曲线相比于空筒鼓泡流化床略微向右偏移,这说明单旋导向挡板对大气泡的破碎作用在一定程度上抑制了气体的短路问题。进一步对停留时间分布的数学特征进行计算和分析,得到气体在鼓泡流化床内的平均停留时间
|
|
表 3 停留时间分布的数学特征 Table 3 Mathematic characteristics of RTD |
采用计算颗粒流体力学(CPFD) 方法耦合Igci曳力模型对有、无两层单旋导向挡板的鼓泡流化床进行模拟,模拟计算得到的轴向和径向时均固含率分布与实验数据较为吻合,表明此方法用来模拟单旋导向挡板鼓泡流化床的三维气固流动可行。使用MS3DATA算法统计和分析了该鼓泡流化床内的气泡平均当量直径沿床高的分布,结果表明,单旋导向挡板对大气泡有一定的破碎作用,有挡板的鼓泡流化床内气泡平均尺寸小于空筒鼓泡流化床。使用空气作为示踪剂考察该鼓泡流化床内的气体返混和停留时间分布,结果表明,两层单旋导向挡板的存在没有明显影响鼓泡流化床内的气体返混,有、无挡板的鼓泡流化床内的气体平均停留时间和方差基本相同,返混程度均与平推流理想反应器接近。
| [1] |
刘中民. 甲醇制烯烃[M]. 北京: 科学出版社, 2015. LIU Z M. Methanol to olefins[M]. Beijing: Science Press, 2015. |
| [2] |
许友好. 催化裂化化学与工艺[M]. 北京: 科学出版社, 2013. XU Y H. Chemistry & Process of catalytic cracking[M]. Beijing: Science Press, 2013. |
| [3] |
郭慕孙, 李洪钟. 流态化手册[M]. 北京: 化学工业出版社, 2008. GUO M S, LI H Z. Handbook of fluidization[M]. Beijing: Chemical Industry Press, 2008. |
| [4] |
LI H, LU X, KWAUK M. Particulatization of gas–solids fluidization[J]. Powder Technology, 2003, 137(1/2): 54-62. |
| [5] |
HARRISON D. Fluidized beds with internal baffles[J]. Fluidization, 1971, 599-626. |
| [6] |
石孝刚, 赵国静, 吴迎亚, 等. 挡板鼓泡床内气泡特性的CFD模拟分析[J]. 石油学报(石油加工), 2019, 36(1): 113-120. SHI X G, ZHAO G J, WU Y Y, et al. CFD simulation of bubbles behavior in baffled bubbling fluidized bed[J]. Acta Petrolei Sinica(Petroleum Processing Section), 2019, 36(1): 113-120. |
| [7] |
GAO J, CHANG J, XU C, et al. CFD simulation of gas solid flow in FCC strippers[J]. Chemical Engineering Science, 2008, 63(7): 1827-1841. DOI:10.1016/j.ces.2007.12.009 |
| [8] |
YANG S, LI H, ZHU Q. Experimental study and numerical simulation of baffled bubbling fluidized beds with Geldart A particles in three dimensions[J]. Chemical Engineering Journal, 2015, 259: 338-347. DOI:10.1016/j.cej.2014.07.055 |
| [9] |
YANG S, PENG L, LIU W, et al. Simulation of hydrodynamics in gas-solid bubbling fluidized bed with louver baffles in three dimensions[J]. Powder Technology, 2016, 296: 37-44. DOI:10.1016/j.powtec.2015.09.026 |
| [10] |
ZHU X, FENG X, ZOU Y, et al. Effect of baffles on bubble behavior in a bubbling fluidized bed for chemical looping processes[J]. Particuology, 2020, 53: 154-167. DOI:10.1016/j.partic.2020.04.003 |
| [11] |
YANG Z, ZHANG Y, ZHANG H. CPFD simulation on effects of louver baffles in a two-dimensional fluidized bed of Geldart A particles[J]. Advanced Powder Technology, 2019, 30(11): 2712-2725. DOI:10.1016/j.apt.2019.08.018 |
| [12] |
WEBER J M, LAYFIELD K J, VAN ESSENDELFT D T, et al. Fluid bed characterization using electrical capacitance volume tomography (ECVT), compared to CPFD Software's Barracuda[J]. Powder Technology, 2013, 250: 138-146. DOI:10.1016/j.powtec.2013.10.005 |
| [13] |
VASHISTH S, AHMADI MOTLAGH A H, TEBIANIAN S, et al. Comparison of numerical approaches to model FCC particles in gas–solid bubbling fluidized bed[J]. Chemical Engineering Science, 2015, 134: 269-286. DOI:10.1016/j.ces.2015.05.001 |
| [14] |
LIM J H, BAE K, SHIN J H, et al. Effect of particle–particle interaction on the bed pressure drop and bubble flow by computational particle-fluid dynamics simulation of bubbling fluidized beds with shroud nozzle[J]. Powder Technology, 2016, 288: 315-323. DOI:10.1016/j.powtec.2015.11.017 |
| [15] |
LIM J H, BAE K, SHIN J H, et al. CPFD simulation of bubble flow in a bubbling fluidized bed with shroud nozzle distributor and vertical internal[J]. Korean Chemical Engineering Research, 2016, 54(5): 678-686. DOI:10.9713/kcer.2016.54.5.678 |
| [16] |
SNIDER D M. An incompressible three-dimensional multiphase particle-in-cell model for dense particle flows[J]. Journal of Computational Physics, 2001, 170(2): 523-549. DOI:10.1006/jcph.2001.6747 |
| [17] |
CROWE C T. Multiphase flow handbook[M]. Boca Raton: CRC Press, 2005.
|
| [18] |
GIDASPOW D. Multiphase flow and fluidization: continuum and kinetic theory descriptions[M]. San Diego: Academic Press, 1994.
|
| [19] |
GAO X, LI T, SARKAR A, et al. Development and validation of an enhanced filtered drag model for simulating gas-solid fluidization of Geldart A particles in all flow regimes[J]. Chemical Engineering Science, 2018, 184: 33-51. DOI:10.1016/j.ces.2018.03.038 |
| [20] |
LI J H, KWAUK M. Particle-fluid two-phase flow: The energy-minimization multi-scale method[M]. Beijing: Metallurgical Industry Press, 1994.
|
| [21] |
IGCI Y, PANNALA S, BENYAHIA S, et al. Validation studies on filtered model equations for gas-particle flows in risers[J]. Industrial & Engineering Chemistry Research, 2011, 51(4): 2094-2103. |
| [22] |
杨帅. 内构件鼓泡流化床中流动结构及其计算机模拟研究[D]. 北京: 中国科学院研究生院(过程工程研究所), 2016. YANG S. Flow structure investigation and computational fluid dynamics simulation for baffled bubbling fluidized beds [D]. Beijing: University of Chinese Academy of Sciences(Institute of process engineering), 2016. |
| [23] |
BAKSHI A, ALTANTZIS C, BATES R B, et al. Multiphase-flow statistics using 3D detection and tracking algorithm (MS3DATA): Methodology and application to large-scale fluidized beds[J]. Chemical Engineering Journal, 2016, 293: 355-364. DOI:10.1016/j.cej.2016.02.058 |
| [24] |
DARTON R, RC D, RD L, et al. Bubble growth due to coalescence in fluidized beds[J]. Transactions of the Institution of Chemical Engineers, 1977, 55: 274-280. |
| [25] |
ROWE P N. Prediction of bubble size in a gas fluidized bed[J]. Chemical Engineering Science, 1976, 31(4): 285-288. DOI:10.1016/0009-2509(76)85073-7 |
| [26] |
MORI S, WEN C Y. Estimation of bubble diameter in gaseous fluidized beds[J]. AIChE Journal, 1975, 21(1): 109-115. DOI:10.1002/aic.690210114 |