近年来,在工业生产控制的需要下,迭代学习控制得到了广泛应用。迭代学习控制是一种基于品质的智能控制方法[1],国内外学者已进行了广泛的理论研究。BONVIN等[2]针对网络传输过程中数据丢失问题,提出迭代学习控制器设计方法,并在实际仿真中证明了所提方法的有效性;刘娇龙等[3]通过引入空间状态微分算子和空间复合能量函数,将自适应控制和迭代学习控制方法相结合,提出了一种空间周期的自适应迭代学习控制算法,并通过严格的数学理论和仿真实验证明了所提方法的有效性;兰天一等[4]提出了区间可调节的变增益加速迭代学习控制方法,从理论上分析了所提算法的有效性,并给出了算法的收敛条件,与传统算法相比,仿真实验验证了该算法具备更快的收敛速度;LEE等[5]提出了迭代学习控制与模型预测控制相结合的方法;FAN等[6]提出将迭代学习控制和广义预测控制相结合的方法;DI等[7]提出了利用偏最小二乘的隐变量模型和迭代学习控制结合的思想,得到了不同质量等级的终点质量指标;SANDIZA等[8]利用H∞控制方法提出了一种鲁棒迭代学习控制器;ZHANG等[9]将鲁棒反馈控制器应用于迭代学习控制器中,并证明了系统的鲁棒稳定性和收敛性。
本文针对间歇过程存在的参数时变问题,提出一种基于Markov参数整定的单神经元自适应迭代学习PID控制策略(2D-ILC-PID),使用Markov参数整定法获取2D-ILC-PID控制器的初始参数,在批次内,采用单神经元控制器对2D-ILC-PID控制器参数进行自适应调节,并充分利用批次间的重复特性,使用历史批次的误差信息来修正当前批次的调节变量,最终提高控制性能。
2 间歇过程系统描述二维系统描述的是在两个独立方向上动态行为的系统。在二维系统的框架下,一个多输入多输出的间歇过程系统通常可以用如下状态空间表达式描述:
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{x}}\left( {t + 1,k} \right) = \left( {\mathit{\boldsymbol{A}} + \Delta \mathit{\boldsymbol{A}}} \right)\mathit{\boldsymbol{x}}(t,k) + \left( {\mathit{\boldsymbol{B}} + \Delta \mathit{\boldsymbol{B}}} \right)\mathit{\boldsymbol{u}}\left( {t,k} \right) + w\left( {t,k} \right)}\\ {\mathit{\boldsymbol{y}}\left( {t,k} \right) = \mathit{\boldsymbol{Cx}}\left( {t,k} \right) + \mathit{\boldsymbol{v}}\left( {t,k} \right)} \end{array}} \right. $ | (1) |
式中,k表示批次,t表示时间;x(t, k)、u(t, k)、y(t, k)分别表示系统在第k批次、第t时刻的状态、输入量和输出量;w(t, k)表示非重复负载扰动;v(t, k)表示非重复测量扰动;A、B、C表示合适维度的系统矩阵。
二维系统的控制目标是适时调整控制输入作用u(t, k),使得系统即使在面临不确定性扰动和噪声的情况下,系统输出y(t, k)都能尽可能准确地跟踪给定目标跟踪曲线。
3 单神经元自适应2D-ILC-PID控制器 3.1 Markov参数优化设计考虑下列线性离散系统:
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{x}}(t + 1,k) = \mathit{\boldsymbol{Ax}}(t,k) + \mathit{\boldsymbol{Bu}}(t,k) + \mathit{\boldsymbol{w}}(t,k)}\\ {\mathit{\boldsymbol{y}}(t,k) = \mathit{\boldsymbol{Cx}}(t,k) + \mathit{\boldsymbol{v}}(t,k)} \end{array}} \right. $ | (2) |
在扰动和测量噪声的情况下,线性离散传函系统表示如下:
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{x}}(t + 1,k) = \mathit{\boldsymbol{Ax}}(t,k) + \mathit{\boldsymbol{Bu}}(t,k)}\\ {\mathit{\boldsymbol{y}}(t,k) = \mathit{\boldsymbol{Cx}}(t,k)} \end{array}} \right. $ | (3) |
| $ \mathit{\boldsymbol{y}}(t,k) = \mathit{\boldsymbol{C}}{\mathit{\boldsymbol{A}}^t}\mathit{\boldsymbol{x}}(0,0) + \sum\limits_{i = 0}^{t - 1} {\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{A}}^{t - \mathit{1} - i}}\mathit{\boldsymbol{Bu}}(i,k)} $ | (4) |
定义矩阵Uk、Yk、Yd、Ek分别表示第k次迭代的输入、输出、期望轨迹和第k次的误差。
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{U}}_k} = {{\left[ {{u_{\rm{k}}}(0),{u_{\rm{k}}}(1), \cdot \cdot \cdot ,{u_{\rm{k}}}(N - 1)} \right]}^{\rm{T}}}}\\ {{\mathit{\boldsymbol{Y}}_k} = {{\left[ {{y_{\rm{k}}}(1),{y_{\rm{y}}}(2), \cdot \cdot \cdot ,{y_{\rm{k}}}(N)} \right]}^{\rm{T}}}}\\ {{\mathit{\boldsymbol{Y}}_d} = {{\left[ {{y_{\rm{d}}}(1),{y_{\rm{d}}}(2), \cdot \cdot \cdot ,{y_{\rm{d}}}(N)} \right]}^{\rm{T}}}}\\ {{\mathit{\boldsymbol{E}}_k} = {{\left[ {{e_{\rm{k}}}(1),{e_{\rm{k}}}(2), \cdot \cdot \cdot ,{e_{\rm{k}}}(N)} \right]}^{\rm{T}}}} \end{array}} \right. $ | (5) |
系统的Markov参数为:hi = CAi-1B (i = 1, 2, ⋯),假设初始状态x(0, 0)=0,那么该离散系统可以表示为:
| $ {\mathit{\boldsymbol{Y}}_{\rm{k}}} = {\mathit{\boldsymbol{H}}_{\rm{p}}} \times {\mathit{\boldsymbol{U}}_{\rm{k}}}$ | (6) |
式中,Hp为由被控对象的Markov参数所构成的矩阵:
| $ {\mathit{\boldsymbol{H}}_{\rm{p}}} = \left[ {\begin{array}{*{20}{c}} {{h_1}}&0&0& \cdots &0\\ {{h_2}}&{{h_1}}&0& \cdots &0\\ {{h_3}}&{{h_2}}&{{h_1}}& \cdots &0\\ \vdots & \vdots & \vdots & \ddots & \vdots \\ {{h_N}}&{{h_{N - 1}}}&{{h_{N - 2}}}& \cdots &{{h_1}} \end{array}} \right] $ | (7) |
该系统的迭代学习控制律由下式更新:
| $ {\mathit{\boldsymbol{u}}_{{\rm{k}} + 1}}(t) = {\mathit{\boldsymbol{u}}_{\rm{k}}}(t) + {k_{\rm{p}}}{\mathit{\boldsymbol{e}}_{\rm{k}}}(t) + {k_{\rm{I}}}{\mathit{\boldsymbol{I}}_{e(k)}} + {k_{\rm{D}}}{\mathit{\boldsymbol{D}}_{e(k)}} $ | (8) |
采用向量形式,迭代学习控制律可以表示为:
| $ {\mathit{\boldsymbol{U}}_{{\rm{k}} + 1}} = {\mathit{\boldsymbol{U}}_{\rm{k}}} + {k_{\rm{p}}}{\mathit{\boldsymbol{E}}_{\rm{k}}} + {k_{\rm{I}}}{\mathit{\boldsymbol{T}}_{\rm{I}}}{\mathit{\boldsymbol{E}}_{\rm{k}}} + {k_{\rm{D}}}{\mathit{\boldsymbol{T}}_{\rm{D}}}{\mathit{\boldsymbol{E}}_{\rm{k}}} $ | (9) |
式中:
| $ {\mathit{\boldsymbol{T}}_1} = \left[ {\begin{array}{*{20}{c}} 1&0&0& \cdots &0\\ 1&1&0& \cdots &0\\ 1&1&1& \cdots &0\\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1&1&1& \cdots &1 \end{array}} \right] $ | (10) |
| $ {\mathit{\boldsymbol{T}}_{\rm{D}}} = \left[ {\begin{array}{*{20}{c}} 1&0&0& \cdots &0\\ { - 1}&1&0& \cdots &0\\ 0&{ - 1}&1& \cdots &0\\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0&0&0& \cdots &1 \end{array}} \right] $ | (11) |
取向量h = [h1, h2, ⋯, hN]T,可以得到:
| $ {\mathit{\boldsymbol{E}}_{k + 1}} = {\mathit{\boldsymbol{E}}_k} - {\mathit{\boldsymbol{H}}_{\rm{p}}}({\mathit{\boldsymbol{U}}_k} - {\mathit{\boldsymbol{U}}_{k + 1}}) $ | (12) |
结合向量形式的迭代控制律表示公式,进一步得到:
| $ {\mathit{\boldsymbol{E}}_{k + 1}} = {\mathit{\boldsymbol{H}}_{\rm{ \mathsf{ δ} }}} \times {\mathit{\boldsymbol{E}}_k} $ | (13) |
其中:
| $ {\mathit{\boldsymbol{H}}_{\rm{ \mathsf{ δ} }}} = \mathit{\boldsymbol{I}} + {k_{\rm{p}}}{\mathit{\boldsymbol{H}}_{\rm{p}}} + {k_{\rm{I}}}{\mathit{\boldsymbol{H}}_{\rm{p}}}{\mathit{\boldsymbol{T}}_{\rm{I}}} + {k_{\rm{D}}}{\mathit{\boldsymbol{H}}_{\rm{D}}}{\mathit{\boldsymbol{T}}_{\rm{D}}} $ | (14) |
其中,kp为比例系数。k1为积分时间常数,kD为微分时间常数。
根据式(13)可以得知,迭代过程收敛条件为:
| $ {\left\| {{\mathit{\boldsymbol{H}}_{\rm{ \mathsf{ δ} }}}} \right\|_i} < 1, i = 1 \ldots \infty $ | (15) |
因此迭代学习控制器参数的设计问题就转化为式(15)的问题,显而易见,
| $ {\left\| {{\mathit{\boldsymbol{H}}_{\rm{ \mathsf{ δ} }}}} \right\|_1} = {\left\| {{\mathit{\boldsymbol{H}}_{\rm{ \mathsf{ δ} }}}} \right\|_\infty } $ | (16) |
所以
定义如下性能优化指标:
| $ J_{{\rm{PID}}}^* = _{{K_{\rm{P}}},{K_{\rm{I}}},{K_{\rm{D}}}}^{\;\;\;\;\;\;\;\;{\rm{Min}}}{J_{{\rm{PID}}}} = _{{K_{\rm{P}}},{K_{\rm{I}}},{K_{\rm{D}}}}^{\;\;\;\;\;\;\;\;{\rm{Min}}}\left\| {{h_{\rm{ \mathsf{ δ} }}}} \right\|_2^2 $ | (17) |
并令gPID = [kI, kp, kD]T,经过计算得到如下结果[10]:
| $ {\mathit{\boldsymbol{g}}_{{\rm{PID}}}} = \left[ \begin{array}{l} {k_{\rm{I}}}\\ {k_{\rm{P}}}\\ {k_{\rm{D}}} \end{array} \right] = {\left[ {\begin{array}{*{20}{c}} {h_{\rm{I}}^{\rm{T}}{h_{\rm{I}}}}&{h_{\rm{I}}^{\rm{T}}h}&{h_{\rm{I}}^{\rm{T}}{h_{\rm{D}}}}\\ {{h^{\rm{T}}}{h_{\rm{I}}}}&{{h^{\rm{T}}}h}&{{h^{\rm{T}}}{h_{\rm{D}}}}\\ {h_{\rm{D}}^{\rm{T}}{h_{\rm{I}}}}&{h_{\rm{D}}^{\rm{T}}h}&{h_{\rm{D}}^{\rm{T}}{h_{\rm{D}}}} \end{array}} \right]^{ - 1}}\left[ \begin{array}{l} {h_1}\\ {h_1}\\ {h_1} \end{array} \right] $ | (18) |
当采用PI型ILC时:
| $ \left[ \begin{array}{l} {k_{\rm{I}}}\\ {k_{\rm{P}}} \end{array} \right] = {\left[ {\begin{array}{*{20}{c}} {h_{\rm{I}}^{\rm{T}}{h_{\rm{I}}}}&{h_{\rm{I}}^{\rm{T}}h}\\ {{h^{\rm{T}}}{h_{\rm{I}}}}&{{h^{\rm{T}}}h} \end{array}} \right]^{ - 1}}\left[ \begin{array}{l} {h_{\rm{1}}}\\ {h_{\rm{1}}} \end{array} \right] $ | (19) |
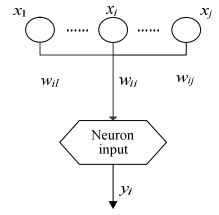
对人脑神经元进行抽象简化后得到称为McCulloch-Pitts模型的人工神经元[11],如图 1所示。
|
图 1 单神经元模型 Fig.1 Scheme of a single neuron model |
图中,x1⋯xi代表神经元接受到的信息,wi1⋯wiN称为连接强度,连接强度称为权,利用某种运算将输入信号的作用结合起来作为神经元输入的总效果,并将该总效果称为“净输入”,用net表示。根据不同的运算方式,净输入的表达方式有很多种,最简单的一种是线性加权求和,用如下式表示:
| $ {\rm{net}} = \sum\limits_{j = 1}^N {{w_{ij}}{x_j} - {\theta _i}} $ | (20) |
式中,
| $ {y_i} = g({\rm{net}}) $ | (21) |
单神经元自适应PID参数调节器通过对连接强度w的调整来实现自适应、自学习能力。连接强度w的调整可以采用不同的学习规则,从而构成不同的参数调节器。本文采用Hebb监督学习规则来实现比例、积分、微分参数的自适应调节[12]:
| $ \Delta {w_{ij}}(k) = \eta \left[ {{y_r}(k) - y(k)} \right]{\delta _i}(k){\delta _j}(k) $ | (22) |
考虑到连接强度
| $ \left\{ {\begin{array}{*{20}{l}} {{w_i}(t,k + 1) = (1 - a){w_i}(t,k) + \eta {\varphi _i}(t,k)}\\ {{\varphi _i}(t,k) = e(t,k)\mathit{\boldsymbol{u}}(t,k){x_i}(t,k)} \end{array}} \right. $ | (23) |
式中,
由上式有:
| $ \Delta {w_i}(t,k) = {w_i}(t,k + 1) - {w_i}(t,k) = - a\left[ {{w_i}(t,k) - \frac{h}{a}e(t,k)\mathit{\boldsymbol{u}}(t,k){x_i}(t,k)} \right] $ | (24) |
构造关于
| $ \frac{{\partial {f_i}}}{{\partial {w_i}}} = {w_i}(t,k) - \frac{\eta }{a}{h_i}\left[ {e(t,k)\mathit{\boldsymbol{u}}(t,k){x_i}(t,k)} \right] $ | (25) |
因此有:
| $ \Delta {w_i}(t, k) = - a\frac{{\partial {f_i}( \cdot )}}{{\partial {w_i}(t, k)}} $ | (26) |
以上推导结果可以发现,连接强度
将上述单神经元自适应PID调节器的算法过程经过规范处理后得到:
| $ \left\{ {\begin{array}{*{20}{l}} {{w_{\rm{p}}}(t,k + 1) = {w_{\rm{p}}}(t,k) + {\eta _{\rm{p}}}\mathit{\boldsymbol{e}}(t,k)\mathit{\boldsymbol{u}}(t - 1,k){x_1}(t,k)}\\ {{w_{\rm{I}}}(t,k + 1) = {w_{\rm{I}}}(t,k) + {\eta _{\rm{I}}}\mathit{\boldsymbol{e}}(t,k)\mathit{\boldsymbol{u}}(t - 1,k){x_2}(t,k)}\\ {{w_{\rm{D}}}(t,k + 1) = {w_{\rm{D}}}(t,k) + {\eta _{\rm{D}}}\mathit{\boldsymbol{e}}(t,k)\mathit{\boldsymbol{u}}(t - 1,k){x_3}(t,k)} \end{array}} \right. $ | (27) |
式中,ωp(t, k),
ωI(t, k),
ωD(t, k)分别代表第k批次的第t时刻的比例、积分、微分系数;ηp, ηI, ηD分别代表比例、积分、微分的学习速率;
| $ \left\{ {\begin{array}{*{20}{l}} {{x_1}(t,k) = \mathit{\boldsymbol{e}}(t,k)}\\ {{x_2}(t,k) = \mathit{\boldsymbol{e}}(t,k) - \mathit{\boldsymbol{e}}(t - 1,k)}\\ {{x_3}(t,k) = \mathit{\boldsymbol{e}}(t,k) - 2\mathit{\boldsymbol{e}}(t - 1,k) + \mathit{\boldsymbol{e}}(t - 1,k - 1)} \end{array}} \right. $ | (28) |
将PID控制和二维迭代学习控制相结合,设计出2D-ILC-PID控制器的控制律:
| $ {u_{{\rm{k}} + 1}}(t) = {u_{\rm{k}}}(t) + {w_{\rm{P}}}(t,k){e_{\rm{k}}}(t) + {w_{\rm{I}}}(t,k)\sum\limits_{j = 1}^t {{e_{\rm{k}}}(j) + } {w_{\rm{D}}}(t,k)\frac{{{\rm{d}}{e_{\rm{k}}}(t)}}{{{\rm{d}}t}} $ | (29) |
式中,
| $ {e_{\rm{k}}}(t) = {y_{\rm{r}}}(t,k) - y(t,k) $ | (30) |
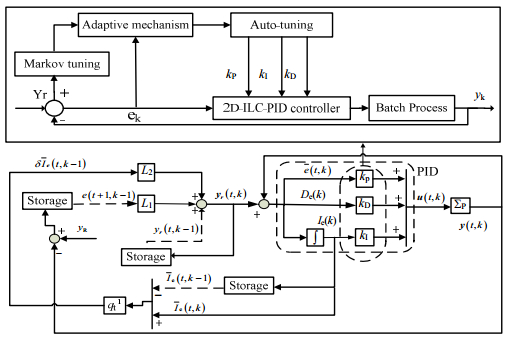
考虑将单神经元自适应PID调节器加入到上述2D-ILC-PID控制器中,基于Markov单神经元自适应的2D-ILC-PID控制方法的结构框图如下:
|
图 2 基于Markov单神经元自适应的2D-ILC-PID控制方法的结构框图 Fig.2 Schematic diagram of a 2D-ILC-PID control method based on Markov single neuron adaptation |
本文采用苯胺与氢气反应生成环己胺(CHA)作为研究对象,其化学反应方程式如下[13]:
| $ \left\{ \begin{align} & {{\text{C}}_{\text{6}}}{{\text{H}}_{\text{7}}}\text{N+3}{{\text{H}}_{\text{2}}}\xrightarrow{{{k}_{1}}}{{\text{C}}_{\text{12}}}{{\text{H}}_{\text{13}}}\text{N} \\ & 2{{\text{C}}_{\text{6}}}{{\text{H}}_{\text{7}}}\text{N+6}{{\text{H}}_{\text{2}}}\xrightarrow{{{k}_{2}}}{{\text{C}}_{\text{12}}}{{\text{H}}_{\text{23}}}\text{N+N}{{\text{H}}_{3}} \\ \end{align} \right. $ | (31) |
CHA产率由下式给出:
| $ {k_{{\rm{CHA}}}} = k{C_{\rm{A}}}{C_{{{\rm{H}}_{\rm{2}}}}} = {C_{\rm{A}}}{C_{{{\rm{H}}_{\rm{2}}}}}{k_0}{e^{ - E/R{T_{\rm{R}}}}} $ | (32) |
式中,kCHA代表苯胺加氢反应中环己胺的产率,kmol·s-1·m-3;CA表示苯胺在反应器中的液相浓度,kmol·m-3;
苯胺加氢反应制备环己胺本征动力学方程如下:
苯胺加氢反应总的质量平衡:
| $ \frac{{{\rm{d}}{V_{\rm{R}}}}}{{{\rm{d}}t}} = {F_{{{\rm{H}}_{\rm{2}}}}}{M_{{{\rm{H}}_{\rm{2}}}}}/\rho $ | (33) |
苯胺加氢反应组分的平衡方程为:
| $ \frac{{{\rm{d}}({V_{\rm{R}}}{C_{\rm{A}}})}}{{{\rm{d}}t}} = - {V_{\rm{R}}}k{C_{\rm{A}}}{C_{{{\rm{H}}_{\rm{2}}}}} $ | (34) |
苯胺加氢氢进料平衡方程为:
| $ \frac{{{\rm{d}}({V_{\rm{R}}}{C_{{{\rm{H}}_{\rm{2}}}}})}}{{{\rm{d}}t}} = {F_{{{\rm{H}}_{\rm{2}}}}} - 3{V_{\rm{R}}}k{C_{\rm{A}}}{C_{{{\rm{H}}_{\rm{2}}}}} $ | (35) |
苯胺加氢反应中反应器的温度平衡方程为:
| $ \frac{{{\rm{d}}({V_{\rm{R}}}{T_{\rm{R}}})}}{{{\rm{d}}t}} = \frac{{{F_{{{\rm{H}}_{\rm{2}}}}}{M_{{{\rm{H}}_{\rm{2}}}}}{T_0}}}{\rho } - \frac{{\lambda {V_{\rm{R}}}k{C_{\rm{A}}}{C_{{{\rm{H}}_{\rm{2}}}}}}}{{\rho {c_{\rm{p}}}}} - \frac{{U{A_{\rm{J}}}({T_{\rm{R}}} - {T_{\rm{J}}})}}{{\rho {c_{\rm{p}}}}} $ | (36) |
苯胺加氢反应中夹套温度平衡方程为:
| $ \frac{{{\rm{d}}({V_{\rm{R}}}{T_{\rm{R}}})}}{{{\rm{d}}t}} = \frac{{{F_{{{\rm{H}}_{\rm{2}}}}}{M_{{{\rm{H}}_{\rm{2}}}}}{T_0}}}{\rho } - \frac{{\lambda {V_{\rm{R}}}k{C_{\rm{A}}}{C_{{{\rm{H}}_{\rm{2}}}}}}}{{\rho {c_{\rm{p}}}}} - \frac{{U{A_{\rm{J}}}({T_{\rm{R}}} - {T_{\rm{J}}})}}{{\rho {c_{\rm{p}}}}} $ | (37) |
上述公式中,各个变量代表的内容如表 1所示:
|
|
表 1 参数描述 Table 1 Parameter description |
由苯胺加氢化学反应方程式可知,苯胺加氢制备环己胺的主副反应均为放热反应。因反应放热,同时苯胺加氢制备环己胺对反应温度又有很高的要求,因此在反应过程中必须及时移出反应热,否则影响CHA的转化率。反应中通过调节冷却水进量和氢气进料流量控制反应的剧烈程度,从而达到控温的需求。
在整个苯胺加氢制备CHA的过程中,包含预热、反应、冷却、出料四个操作阶段。在预热阶段,苯胺(反应物A)被一次性加入到间歇反应器中,此后便开始预加热,直到反应器内的温度达到预设值,随后氢气(反应物B)以恒定速率将添加到反应器中,在此期间,间歇反应器内的温度必须恒定在设定值,直至反应物被完全耗尽。
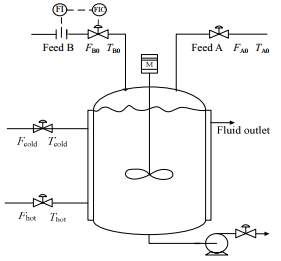
|
图 3 苯胺加氢反应器模型 Fig.3 Schematic diagram of the experimental setup for aniline hydrogenation reaction |
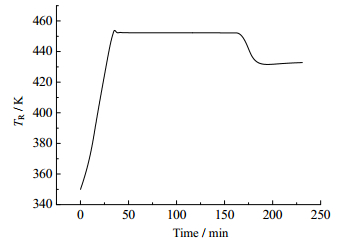
参照文献[13],获取最适合苯胺加氢间歇反应的温度操作曲线,如图 4所示。从图中可知,苯胺(反应物A)以初始温度350 K被加入到间歇反应器中,随即被加热至反应温度设定值450 K,此时氢气(反应物B)以恒定速率加入到反应器中,直至苯胺被完全耗尽,出料阶段温度稳定在430 K。
|
图 4 苯胺加氢反应器模拟操作轨迹 Fig.4 Simulated operation trace of the aniline hydrogenation reactor |
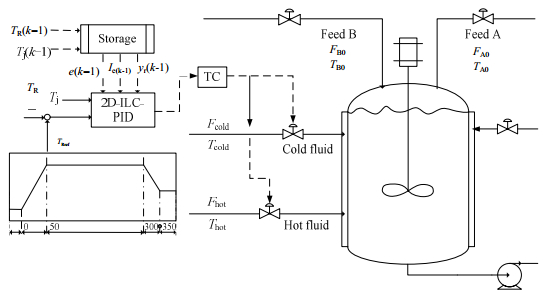
在苯胺加氢间歇反应体系中,系统的控制目标是实现产品转化率和最终产品质量的一致性,控制目标可间接通过控制反应器温度跟踪预设轨迹实现,在间歇补料反应操作过程中,考虑两个操作变量:冷流体和热流体流速。间歇过程单神经元自适应2D-ILC-PID控制框图如下图所示:
|
图 5 苯胺加氢单神经元自适应2D-ILC-PID控制 Fig.5 Schematic diagram of a single-neuron adaptive 2D-ILC-PID control of aniline hydrogenation |
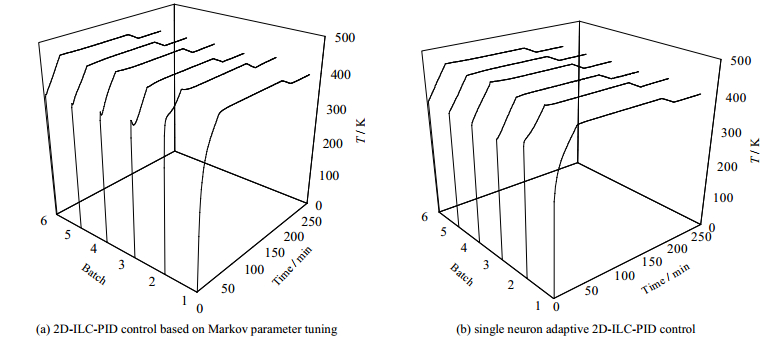
为了验证本文中提出的基于Markov参数整定的单神经元自适应2D-ILC-PID控制策略的有效性,基于上述苯胺加氢反应的严格机理模型,采用MATLAB软件建立间歇反应仿真平台,使用单神经元自适应2D-ILC-PID控制方法,实现环己胺制备过程中精确的温度控制。实验效果如下图所示:
|
图 6 反应器温度输出响应曲线 Fig.6 Output response curves of reactor temperatures |
实验结果表明,无论是采用基于Markov参数整定法的2D-ILC-PID控制方法,还是单神经元自适应2D-ILC-PID控制方法,都能够取得较为理想的温度控制效果,两种控制方法单从粗略的控制效果来看,并没有明显的优劣差距。
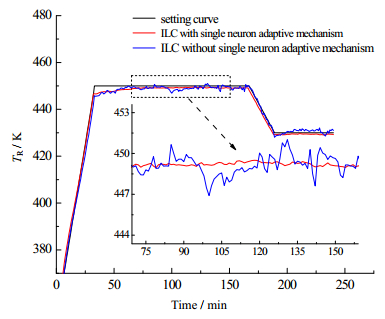
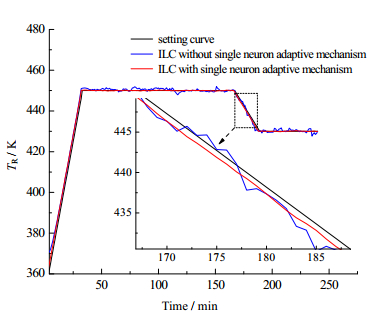
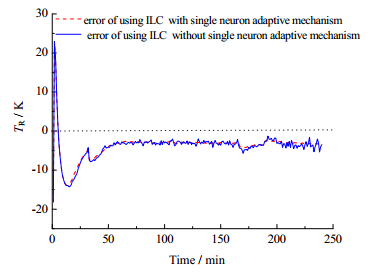
5.2 对比测试结果分析从理论上讲,单神经元自适应2D-ILC-PID控制方法是从基于Markov参数整定法的2D-ILC-PID控制方法发展衍生而来,克服了2D-ILC-PID控制方法无法针对外界环境的改变做出对控制器中比例、积分、微分参数微调的缺陷,其适应性应该会明显优于后者,为验证这一假设,单独提取出第5、10批次的所有跟踪数据,结果如图 7、8。
|
图 7 第5批次温度跟踪曲线对比 Fig.7 Comparison of the 5th batch temperature tracking curves |
|
图 8 第10批次温度跟踪曲线对比 Fig.8 Comparison of the 10th batch temperature tracking curves |
|
图 9 第5批次温度跟踪效果对比 Fig.9 Comparison of the 5th batch temperature tracking results |
|
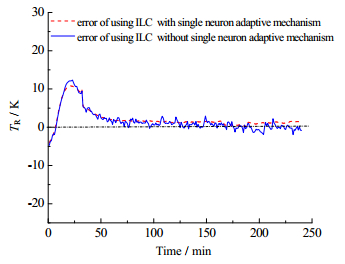
图 10 第10批次温度跟踪效果对比 Fig.10 Comparison of the 10th batch temperature tracking results |
|
|
表 2 批次控制性能比较 Table 2 Comparison of batch control performance |
结果表明:基于Markov参数整定的单神经元自适应2D-ILC-PID控制方法能够进一步实现间歇补料反应器温度的精确跟踪,并且随着批次方向的学习,有效降低跟踪误差,较大程度上改善了控制系统的控制性能。
6 结语本文针对间歇过程存在的参数时变问题,在二维迭代学习PI控制的基础上,设计了基于Markov参数自整定的单神经元自适应PID迭代学习控制策略,采用Markov参数法离线整定控制的参数初值,在批次内,采用单神经元自适应调节机制对2D-ILC-PID控制器参数进行在线自适应调节,最后将该控制方法应用在环己胺制备反应过程进行仿真验证,通过对比分析实验仿真结果,验证了所提控制策略能够有效实现反应器温度的精确跟踪。
| [1] |
LIU T, GAO F R. Industrial process identification and control design[M]. Berlin: Springer-Verlage, 2012.
|
| [2] |
BONVIN D, SRINIVASAN B, HUNKELER D. Control and optimization of batch processes[J]. IEEE Control Systems, 2006, 26(6): 34-45. DOI:10.1109/MCS.2006.252831 |
| [3] |
刘娇龙, 董新民, 薛建平, 等. 一类不确定运动系统的空间迭代学习控制[J]. 控制理论与应用, 2017, 2(2): 197-204. LIU J L, DONG X M, XUE J P, et al. Spatial iterative learning control for a class of uncertain motion systems[J]. Control Theory & Applications., 2017, 2(34): 197-204. |
| [4] |
兰天一, 林辉. 区间可调节的变增益加速迭代学习控制[J]. 系统工程与电子技术, 2016, 39(4): 883-887. LAN T Y, LIN H. Accelerated iterative learning control algorithm with variable gain and adjustment of learning interval[J]. Systems Engineering and Electronics., 2016, 39(4): 883-887. |
| [5] |
LEE J H, LEE K S. Iterative learning control applied to batch processes:An overview[J]. Control Engineering Practice, 2007, 15(10): 1306-1318. DOI:10.1016/j.conengprac.2006.11.013 |
| [6] |
FAN L, WANG H Q, SONG Z H, et al. Iterative optimal control for batch process based on generalized predictive control[J]. Control and Instruments in Chemical Industry, 2006, 33(2): 25-28. |
| [7] |
DI L Q, XIONG Z H. Iterative optimal control for final product qualities of batch processes based on multi-way PLS model[J]. Control and Instruments in Chemical Industry, 2007, 34(2): 10-12. |
| [8] |
SANZIDA N, NAGY Z K. Iterative learning control for the systematic design of supersaturation controlled batch cooling crystallisation processes[J]. Computers and Chemical Engineering, 2013, 59(SI): 111-121. |
| [9] |
ZHANG L, LIU S. Basis function based adaptive iterative learning control for non-minimum phase systems[J]. Acta Automatica Sinica, 2014, 40(12): 2716-2725. |
| [10] |
李仁俊, 韩正之, 唐厚君. 一类迭代学习控制的自适应参数优化[J]. 系统仿真学报, 2015, 17(8): 216-223. LI R J, HAN Z Z, TANG H J. Adaptive parameter optimization of a class of iterative learning control[J]. Journal of System Simulation, 2015, 17(8): 216-223. |
| [11] |
梁中华, 王鑫, 任敏, 等. 一种改进的神经元PID自适应控制[J]. 沈阳工业大学学报, 2003, 25(5): 417-419. LIANG Z H, WANG X, REN M, et al. An improved neuron PID adaptive control[J]. Journal of Shenyang University of Technology, 2003, 25(5): 417-419. DOI:10.3969/j.issn.1000-1646.2003.05.017 |
| [12] |
吴志敏, 李书臣. 基于动态递归神经网络的自适应PID控制[J]. 控制工程, 2004, 3(11): 216-219. WU Z M, LI S C. Adaptive PID control based on dynamic recurrent neural network[J]. Control Engineering of China, 2004, 3(11): 216-219. |
| [13] |
WILLIAM L L. Chemical reactor design and control[M]. Hoboken: John Wiley & Sons, Inc., 2007.
|




