2. 流体动力与机电系统国家重点实验室, 浙江 杭州 310027
2. State Key Laboratory of Fluid Power and Mechatronic Systems, Zhejiang University, Hangzhou 310027, China
液滴微流控技术即微流控芯片中利用2种以上互不相溶的液体相互作用生成高度分散的液滴。该操作下,每个液滴均可以作为独立的反应器进行控制和分析。与传统技术相比,该技术能够极大地提高反应体系的传热、传质效率,减少实验所需试剂的消耗量,实现样本的并行处理和高通量筛选[1-2]。尽管液滴微流控技术因独特的优势被广泛应用于有机合成、纳米颗粒制备、蛋白质结晶、高通量药物筛选等领域[3-4],但是,由于流体物理特性、微通道特征以及操作条件的多样性,增加了微通道内两相流流型的不确定性[5-6]。微通道内,连续相流体和分散相流体相互作用,界面形态受流体流速和流体物理特性的影响,呈现不同的流型,包括液滴流(弹状流、滴状流)、喷射流、环状流、平行流等[7-8]。同时,在液滴流流型下,受多种参数的影响,对于液滴形貌精确调控也存在一定的难度。为此,许多学者对微尺度下液-液两相流流动特性进行研究[9-13]。
两相流体黏度是影响两相流流型的一个重要参数。近年来,针对流体黏度对两相流流型影响开展的研究主要包括两相流流型在牛顿/牛顿流体体系中的变化、两相流流型在牛顿/非牛顿流体体系中的变化、两相流流型在高黏度/低黏度流体体系的变化、两相流流型在低黏度/低黏度流体体系的变化[14-16]。其中,高黏度流体指黏度大于25 mPa·s的流体[17]。
Yagodnitsyna等[18]考察共流T型微通道内煤油/水(低黏度/低黏度)、石蜡油/水(高黏度/低黏度)、石蜡油/蓖麻油(高黏度/高黏度) 3种流体体系下的两相流流型。在3种流体体系下,观察到的共同流型有平行流、塞状流和弹状流。在石蜡油/蓖麻油下,同样观察到蜿蜒流。Derzsi等[19]对比两相流流型在牛顿/牛顿流体和牛顿/非牛顿流体体系中的变化。在牛顿/非牛顿流体体系中,采用非牛顿流体作为连续相,且流体黏度与牛顿/牛顿流体体系中的连续相流体相近。研究结果表明在牛顿/牛顿流体体系中更易形成规则的滴状流。Yao等[17]对微通道内含离子液体的液-液两相流流体流动特性进行系统的总结,分析离子液体分别作为连续相流体和分散相流体时,微通道内流体流动,并与常规两相体系进行了对比。
目前,尽管许多学者针对不同黏度下的液-液两相体系开展了大量研究,但针对大黏度范围内的两相体系研究仍报道较少。本研究通过对已有文献报道中的两相体系进行整理,利用实验和数值模拟相结合的方法,对大黏度范围内液-液两相流流动进行研究,研究十字型微通道内两相黏度变化对流型的影响,相关研究结果对于微尺度液-液两相流流型控制,尤其是高黏度流体体系的微尺度操控具有重要意义。
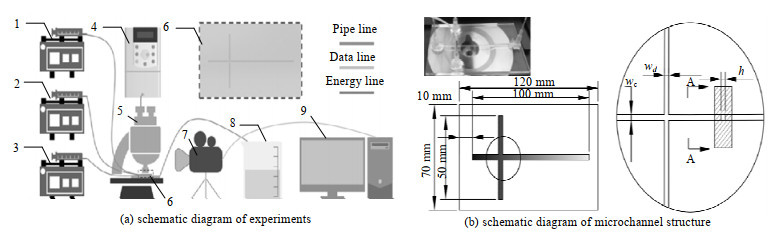
2 研究方法 2.1 实验操作介绍液滴流型研究实验装置如图 1所示,其主要设备包括3台高精度注射泵(SPLab02,保定申辰泵业有限公司)、高速摄像机(D2000,OPLENIC)、电子显微镜(XD系列,宁波舜宇仪器有限公司)、微通道以及冷光源。本实验中采用由透明树脂制作的正方形截面十字型微通道,其截面尺寸为1 000 μm× 1 000 μm。
|
图 1 液滴流型研究实验装置 Fig.1 Experimental devices for droplet flow patterns 1, 2. syringe pump 3. syringe pump 4. cold light illuminator 5. microscope 6. microchannel 7. high-speed camera 8. waste collecting bottle 9. computer |
实验中,分散相流体为去离子水,连续相流体为2种不同黏度的二甲基硅油,物性参数如表 1所示,两相间表面张力由悬滴法测量。
|
|
表 1 两相流体物性参数 Table 1 Properties of two-phase fluids |
采用ANSYS FLUENT中流体体积模型(volume of fluid,VOF)开展数值模拟研究。该模型被众多学者用来研究微通道内液-液两相流流动[10, 13, 20]。本课题组在之前的研究中同样采用该方法开展微通道内液-液两相流流动研究[21-23],故此不再赘述。数值模拟过程中,考虑到结构的对称性,建立1/2模型,对称面设置为对称边界。设定连续相入口和分散相入口为速度入口,无梯度分布,出口为自由出口,壁面无滑移。
本研究对已有文献报道数据进行搜集整理,选取28组两相体系来研究不同流体黏度下流型转换机制。如图 2所示为数值模拟中所涉及两相体系流体黏度,图中μc为连续相流体的黏度,μd为分散相流体的黏度。

|
图 2 两相体系流体黏度 Fig.2 Fluid viscosities of two phase system used in simulation |
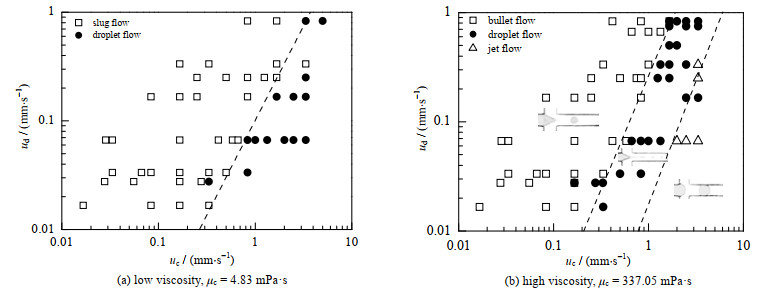
图 3为以两相流速为坐标轴绘制的2种连续相流体黏度下液-液两相流流型图。图中uc为连续相流体的速度,ud为分散相流体速度。在相同的流速范围内,当连续相流体黏度为4.83 mPa·s时,微通道内观察到的流型有弹状流和滴状流,而当连续相流体黏度为337.05 mPa·s时,微通道内观察到的流型有子弹流、滴状流和喷射流。连续相流体黏度增加,其施加在分散相流体上的剪切力增加,加速了分散相流体颈部断裂频率,加剧了微通道内液-液两相流流型的不稳定性。因此,相同流速范围内,连续相为高黏度流体的体系中,弹状流(子弹流)范围变窄,随着连续相流体流速的增加,液滴尺寸不断减小,两相流型由弹状流过渡为滴状流。
|
图 3 2种连续相流体黏度下两相流流型图 Fig.3 Two phase flow patterns for continuous phase with low viscosity and high viscosity |
实验还观察到,在弹状流流型下,连续相流体黏度为337.05 mPa·s,液滴的形状更趋向于子弹型,即液滴头部半径rfront小于液滴尾部半径rrear,如图 4所示。

|
图 4 2种连续相流体黏度下液滴形状示意图ud = 0.33 mm·s−1 Fig.4 Droplet shape for continuous phase with low viscosity and high viscosity |
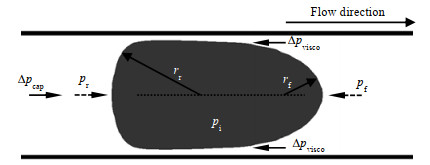
随着连续相流体流速增加,液滴尺寸减小,液滴头部半径和尾部半径均逐渐减小。液滴在微通道下游匀速流动时,主要受到2种力的作用,分别是表面张力引起的毛细驱动压差Δpcap以及流体黏性阻力引起的压差Δpvisco,如图 5所示。根据Young-Laplace方程,液滴前后两个凸液面的压差分别为
| $ {p_{\text{i}}} - {p_{\text{f}}} = \sigma (\frac{1}{{({2 \mathord{\left/ {\vphantom {2 h}} \right. } h})}} + \frac{1}{{{r_{\text{f}}}}}) $ | (1) |
| $ {p_{\text{i}}} - {p_{\text{r}}} = \sigma (\frac{1}{{({2 \mathord{\left/ {\vphantom {2 h}} \right. } h})}} + \frac{1}{{{r_{\text{r}}}}}) $ | (2) |
|
图 5 液滴流动过程中受力示意图 Fig.5 Forces involved in droplet flow |
式中:σ为表面张力,mN·m−1;pi、pf和pr分别为液滴内部压力、液滴前端压力和液滴后端压力,mPa;h、rf和rr分别为微通道深度、液滴前端半径和液滴后端半径,μm。由式(1)和(2)可得毛细驱动压差为
| $ \Delta {p_{{\text{cap}}}} = {p_{\text{r}}} - {p_{\text{f}}} = \sigma (\frac{1}{{{r_{\text{f}}}}} - \frac{1}{{{r_{\text{r}}}}}) $ | (3) |
流体黏性阻力所引起的压差由Hagen-Poiseuille方程求得,如式(4)所示:
| $ \Delta {p_{{\text{visco}}}} = O(\frac{{{\mu _{\text{c}}}{u_{{\text{total}}}}L}}{{hw}}) $ | (4) |
式中:O为确定的函数关系;L为液滴长度,μm;w为液滴宽度,μm;utotal为微通道截面流体流速,mm·s−1,由式(5)计算所得
| $ {u_{{\text{total}}}} = \frac{{{q_{V,{\text{c}}}} + {q_{V,{\text{d}}}}}}{A} $ | (5) |
式中:qV, c和qV, d分别为连续相流体体积流量和分散相流体体积流量,mL·h−1;A为微通道截面面积,μm2;液滴在微通道内流动时,液滴形状在毛细驱动力和黏性阻力的相互作用下保持稳定,则有Δpcap ≈ Δpvisco,即
| $ \sigma (\frac{1}{{{r_{\text{f}}}}} - \frac{1}{{{r_{\text{r}}}}}) \approx O(\frac{{{\mu _{\text{c}}}{u_{{\text{total}}}}L}}{{hw}}) $ | (6) |
式(6)等式左边为起驱动作用的毛细压力;右边为黏性阻力。由式(6)可以看出,液滴前后两个凸液面曲率差
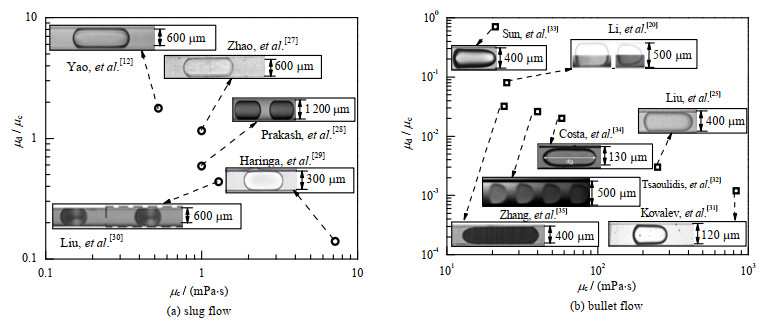
通过对文献数据进行整理,图 6绘制了不同两相体系下,微通道内观察到的液滴流型。当连续相流体黏度较低(μc < 10 mPa·s)时,微通道内液滴流型通常为弹状流[12, 27-30],此时液滴前后凸液面弯曲程度大致相同。当连续相流体黏度较高(μc > 10 mPa·s)时,微通道内液滴流型多为子弹流[20, 25, 31-35]。
|
图 6 不同黏度下微通道内液滴形状 Fig.6 Droplet shape under different viscosities |
为了进一步考察流体黏度对液滴生成特性的影响,本节以28种两相体系为研究对象,利用数值模拟方法考察了十字型微通道内体黏度对液滴生成特性的影响。研究中,两相流体流速始终保持一致,ud = uc = 25 mm·s−1。所涉及两相体系分别来自不同文献,其具体数值如图 2所示。
在微通道下游,观察到的流型有:弹状流、子弹流、不规则流和环状流,如图 7所示。

|
图 7 不同黏度下微通道下游流型图 Fig.7 Flow patterns in downstream of the microchannel under different viscosities |
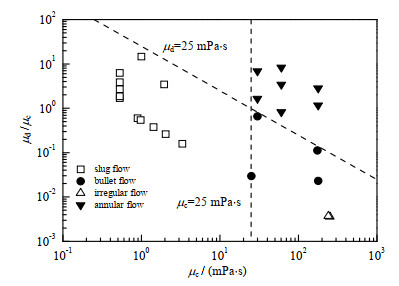
图 8为基于两相流体黏度变化绘制的流型图。从图中可以看出,相同操作条件下,当两相流体均为常规流体时,两相表面张力占据主导地位,此时通道内流型为弹状流,液滴前后两端近似半球形。随着连续相流体黏度的增加,连续相流体的黏性剪切作用增加,使得分散相液滴的生成频率增加,液滴尺寸减小,且液滴前后两端半径差距进一步增加,液滴形状近似子弹流。当连续相流体黏度进一步增加,远大于分散相流体黏度时,微通道内分散相流体受到连续相流体黏性剪切力,呈不规则流动。而当连续相和分散相流体均为高黏度流体时,流型呈现环状流。
|
图 8 基于两相流体黏度的流型图 Fig.8 Flow pattern maps based on two-phase fluid viscosities |
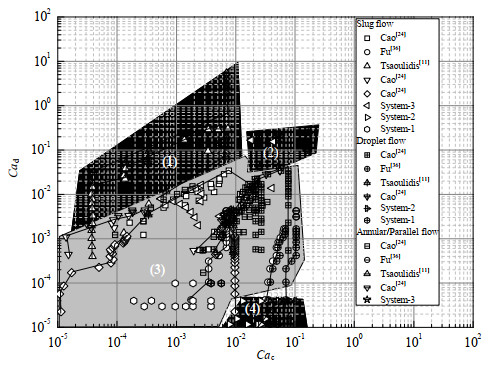
图 9为基于两相毛细数的流型图,图中Cac为连续相的毛细数,Cad为分散相的毛细数。其中,区域(3)中两相流体均为常规流体,区域(1)中分散相流体为高黏度流体,区域(4)中连续相流体为高黏度流体,区域(2)中两相流体均为高黏度流体,其他操作参数如表 2所示,表中,dh为微通道水力直径。
|
图 9 基于两相毛细数的流型图 Fig.9 Flow pattern maps based on two-phase Capillary numbers |
|
|
表 2 操作参数 Table 2 Operating parameters used in different literatures |
结合图 9和表 2可以看出,当两相流体均为常规流体时,操作参数变化(如两相流量)对流型转换的影响相对较弱。随着连续相毛细数增加,微通道内流型由弹状流向滴状流过渡。如图 10中灰色区域所示,当连续相毛细数和分散相毛细数由1×10−5分别增加到0.001和0.01时,微通道内两相流流型由弹状流开始向环状流转换。与常规流体相比,当两相流体有一相(或两相)为高黏度流体时,微通道内两相流流型受操作参数变化影响较大。高黏度流体的存在,加剧了两相界面的不稳定性。如图 10所示,t为时间,两相体系存在高黏度流体时,随着两相毛细数的变化,两相流流型极易向不规则流和环状流转换。如图 9区域(1)所示,当连续相毛细数为4×10−5时,分散相毛细数仅由0.01增加到0.02,两相流流型就由弹状流向环状流转换。
|
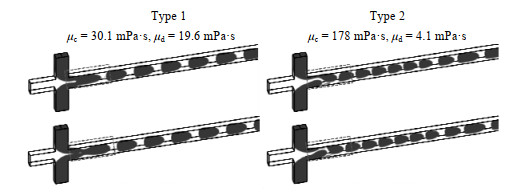
图 10 子弹流形成过程 Fig.10 Forming process of bullet flow |
十字型微通道内,两相流体流入微通道的方式通常为连续相流体经由竖直通道流入,分散相流体经由水平通道流入[24-25, 37]。本研究考察了连续相流体经由水平通道流入,两股分散相流体经由垂直通道流入时,微通道内的液-液两相流型。在该布置方式下,可以将十字型微通道看作2个T型微通道的组合。这样当流体流入微通道时,连续相流体分别和两股分散相流体相互剪切。则在十字微通道交叉口处,会出现2种情况,即:两股分散相流体在交叉口处融合,在连续相流体的剪切作用下,生成分散相液滴,如图 10中方式1所示;两股分散相流体在交叉口处不融合,连续相流体与两股分散相流体分别作用,分散相液滴在微通道内交替形成如图 10中方式2所示。对于方式1,分散相的两股流体在十字交叉口处融合,并与连续相流体相互作用,形成的子弹流包含分散相的两股流体。对于方式2,尽管分散相的两股流体以相同的速度注入微通道中,但是在十字交叉口处并未出现两股流体的融合。两股分散相流体分别与连续相流体相互作用,在微通道下游交替形成子弹流。
此外,随着连续相流体黏度的进一步增加,两股分散相流体在十字交叉口处分别被连续相流体剪切形成不规则液滴,如图 11(a)、(b)所示,而在微通道下游,相邻的液滴在流动过程中,位于上游的液滴始终追赶其前面的液滴,直至两液滴相邻界面破裂并融合,如图 11(c)所示。两液滴融合之后,继续在通道下游流动,融合后的液滴界面逐渐趋于稳定,如图 11(d)、(e)所示。这一液滴融合方式与Liu等[25]的相同两相体系下观察到的液滴融合现象一致,如图 11(f)所示。不同的是Liu等[25]的实验中分散相流体经由水平通道进入。

|
图 11 伴随液滴融合的流动过程 Fig.11 Flow process with droplet coalescence μc = 251.76 mPa·s, μd = 0.89 mPa·s |
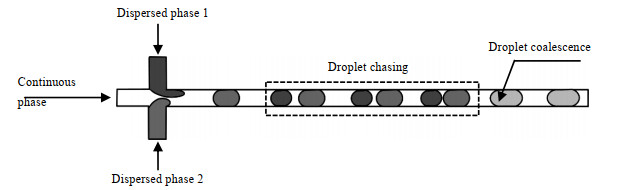
与常规方式相比,分散相流体由垂直通道流入微通道,当连续相流体黏度远大于分散相流体黏度时,由于连续相流体的黏性剪切作用,两股分散相流体经由两垂直通道流入时,在十字交叉口处两股分散相流体并未融合,而是分别与连续相流体相互作用,形成分散的液滴,如图 10方式2和图 11(a)~(e)所示。基于以上发现,可以推测,通过调控两相流速,可以利用该操作方式实现液滴的融合。本研究中,两股分散相流体采用相同的速度流入微通道,因此在连续相的黏性剪切作用下形成大小相同的液滴。当两股分散相流体以不同的流速流入微通道时,则会在连续相的黏性剪切作用下,形成大小不同的液滴。液滴在微通道内流动时,由于液膜的存在,大小不同的液滴其流速也会存在差异,尺寸小的液滴其实际流速较大[18, 20]。因此,当微通道内两股分散相流体以不同速度流入微通道,在连续相的剪切作用下形成大小不同的液滴,由于液滴实际流速的差异,大小液滴在微通道内流动时,小液滴会追赶大液滴,直至融合,如图 12所示。这一方式将为高黏度流体流动操控提供新思路,通过合理调控两相流速,可以实现不依赖于复杂微通道结构的液滴被动融合。
|
图 12 液滴融合示意图 Fig.12 Schematic diagram of droplet coalescence |
本研究结合文献中液-液两相流体体系,研究了流体黏度对两相流流型的影响。主要研究结果如下:
(1) 相同流速范围内,当连续相流体黏度较高时,两相流流型更易受流速变化的影响,随着连续相流体流速增加,连续相为高黏度流体的体系中,弹状流(子弹流)范围变窄。液滴在微通道内流动过程中,液滴形状受表面张力和黏性剪切力的平衡而保持稳定。当连续相流体黏度较高时,由于较大的黏性剪切力,液滴的形状多数为子弹形。
(2) 两相体系中存在高黏度流体时,会加剧两相界面的不稳定性,液-液两相流流型极易受操作参数(如两相流量)变化的影响。弹状流或滴状流等稳定流型极易向不规则流和环状流转换。如当连续相毛细数保持不变时,分散相毛细数只要发生微小的增加,就会引起两相流流型由弹状流向环状流过渡。结合文献数据,绘制了以(Cac·Wed)α为横坐标、Cad为纵坐标的流型转换图谱。
(3) 当连续相流体经由水平通道进入微通道,两股分散相流体经由垂直通道进入微通道时,通过调节两相流速,可以使得微通道内交替形成大小不同的液滴。两液滴在微通道内流动时,小液滴追赶大液滴进而完成液滴融合。该方法可以为液滴被动融合提供新思路。后续研究中,可针对具体的两相体系,开展该方式下液-液两相流流动的研究,考察两相流体流速变化对液滴交替形成的影响,探讨两相流速和液滴交替形成的关系,并开展液滴高效融合研究。
| [1] |
刘卫孝, 高福磊, 朱勇, 等. 微通道反应器合成二缩三乙二醇二硝酸酯的工艺[J]. 高校化学工程学报, 2020, 34(6): 1430-1435. LIU W X, GAO F L, ZHU Y, et al. Synthesis of triethylene glycol dinitrate in a micro-channel reactor[J]. Journal of Chemical Engineering of Chinese Universities, 2020, 34(6): 1430-1435. DOI:10.3969/j.issn.1003-9015.2020.06.013 |
| [2] |
张民, 张正炜, 张艳红. 液滴微流控技术制备功能型微球的研究进展[J]. 高校化学工程学报, 2020, 34(5): 1102-1112. ZHANG M, ZHANG Z W, ZHANG Y H. Research progress on functional microsphere preparation by droplet microfluidic technology[J]. Journal of Chemical Engineering of Chinese Universities, 2020, 34(5): 1102-1112. |
| [3] |
SZYMBORSKI T, JANKOWSKI P, GARSTECKI P. Teflon microreactors for organic syntheses[J]. Sensors and Actuators B: Chemical, 2018, 255: 2274-2281. DOI:10.1016/j.snb.2017.09.035 |
| [4] |
王辉, 汤勇, 余建军, 等. 相变传热微通道技术的研究进展[J]. 机械工程学报, 2010, 46(24): 101-106. WANG H, TANG Y, YU J J, et al. Recent advances of the phase change micro-channel cooling structure[J]. Journal of Mechanical Engineering, 2010, 46(24): 101-106. |
| [5] |
SATTARI-NAJAFABADI M, NASR ESFAHANY M, WU Z, et al. Mass transfer between phases in microchannels: A review[J]. Chemical Engineering and Processing-Process Intensification, 2018, 127: 213-237. DOI:10.1016/j.cep.2018.03.012 |
| [6] |
钱锦远, 李晓娟, 吴赞, 等. 微通道内液-液两相流流型及传质的研究进展[J]. 化工进展, 2019, 38(4): 1624-1633. QIAN J Y, LI X J, WU Z, et al. Research progress on flow regimes and mass transfer of liquid-liquid two-phase flow in microchannels[J]. Chemical Industry and Engineering Progress, 2019, 38(4): 1624-1633. DOI:10.16085/j.issn.1000-6613.2018-0826 |
| [7] |
ZHU P, WANG L. Passive and active droplet generation with microfluidics: A review[J]. Lab on Chip, 2016, 17(1): 34-75. |
| [8] |
QIAN J Y, LI X J, WU Z, et al. A comprehensive review on liquid–liquid two-phase flow in microchannel: Flow pattern and mass transfer[J]. Microfluidics and Nanofluidics, 2019, 23(10): 1-10. |
| [9] |
DAREKAR M, SINGH K K, MUKHOPADHYAY S, et al. Liquid–liquid two-phase flow patterns in Y-junction microchannels[J]. Industrial & Engineering Chemistry Research, 2017, 56(42): 12215-12226. |
| [10] |
王维萌, 马一萍, 陈斌. 十字交叉微通道内微液滴生成过程的数值模拟[J]. 化工学报, 2015, 66(5): 1633-1641. WANG W M, MA Y P, CHEN B. Numerical simulation of droplet generation in crossing micro-channel[J]. CIESC Journal, 2015, 66(5): 1633-1641. |
| [11] |
TSAOULIDIS D, ANGELI P. Effect of channel size on liquid-liquid plug flow in small channels[J]. AIChE Journal, 2016, 62(1): 315-324. DOI:10.1002/aic.15026 |
| [12] |
YAO C, LIU Y, XU C, et al. Formation of liquid–liquid slug flow in a microfluidic T-junction: Effects of fluid properties and leakage flow[J]. AIChE Journal, 2018, 64(1): 346-357. DOI:10.1002/aic.15889 |
| [13] |
SONTTI S G, ATTA A. CFD analysis of microfluidic droplet formation in non–Newtonian liquid[J]. Chemical Engineering Journal, 2017, 330: 245-261. DOI:10.1016/j.cej.2017.07.097 |
| [14] |
魏丽娟, 朱春英, 付涛涛, 等. T型微通道内液滴尺寸的实验测定与关联[J]. 高校化学工程学报, 2013, 27(2): 517-523. WEI L J, ZHU C Y, FU T T, et al. Measurement and correlation of pressure drop of liquid-liquid two-phase flow in microchannels[J]. Journal of Chemical Engineering of Chinese Universities, 2013, 27(2): 517-523. |
| [15] |
WEHKING J D, GABANY M, CHEW L, et al. Effects of viscosity, interfacial tension, and flow geometry on droplet formation in a microfluidic T-junction[J]. Microfluidics and Nanofluidics, 2014, 16(3): 441-453. DOI:10.1007/s10404-013-1239-0 |
| [16] |
ZHANG Q, LIU H, ZHAO S, et al. Hydrodynamics and mass transfer characteristics of liquid–liquid slug flow in microchannels: The effects of temperature, fluid properties and channel size[J]. Chemical Engineering Journal, 2019, 358: 794-805. DOI:10.1016/j.cej.2018.10.056 |
| [17] |
YAO C, ZHAO Y, CHEN G. Multiphase processes with ionic liquids in microreactors: hydrodynamics, mass transfer and applications[J]. Chemical Engineering Science, 2018, 189: 340-359. DOI:10.1016/j.ces.2018.06.007 |
| [18] |
YAGODNITSYNA A A, KOVALEV A V, BILSKY A V. Flow patterns of immiscible liquid-liquid flow in a rectangular microchannel with T-junction[J]. Chemical Engineering Journal, 2016, 303: 547-554. DOI:10.1016/j.cej.2016.06.023 |
| [19] |
DERZSI L, KASPRZYK M, PLOG J P, et al. Flow focusing with viscoelastic liquids[J]. Physics of Fluids, 2013, 25(9): 92001. DOI:10.1063/1.4817995 |
| [20] |
LI Q, ANGELI P. Experimental and numerical hydrodynamic studies of ionic liquid-aqueous plug flow in small channels[J]. Chemical Engineering Journal, 2017, 328: 717-736. DOI:10.1016/j.cej.2017.07.037 |
| [21] |
QIAN J Y, LI X J, WU Z, et al. Slug formation analysis of liquid–liquid two-phase flow in T-junction microchannels[J]. Journal of Thermal Science and Engineering Applications, 2019, 11(5): 051017. DOI:10.1115/1.4043385 |
| [22] |
QIAN J Y, LI X J, GAO Z, et al. Mixing efficiency analysis on droplet formation process in microchannels by numerical methods[J]. Processes, 2019, 7(1): 33. DOI:10.3390/pr7010033 |
| [23] |
QIAN J, LI X, GAO Z, et al. Mixing efficiency and pressure drop analysis of liquid-liquid two phases flow in serpentine microchannels[J]. Journal of Flow Chemistry, 2019, 9(3): 187-197. DOI:10.1007/s41981-019-00040-1 |
| [24] |
CAO Z, WU Z, SUNDÉN B. Dimensionless analysis on liquid-liquid flow patterns and scaling law on slug hydrodynamics in cross-junction microchannels[J]. Chemical Engineering Journal, 2018, 344: 604-615. DOI:10.1016/j.cej.2018.03.119 |
| [25] |
LIU C, ZHANG Q, ZHU C, et al. Formation of droplet and "string of sausages" for water-ionic liquid ([PF6]) two-phase flow in a flow-focusing device[J]. Chemical Engineering and Processing - Process Intensification, 2018, 125: 8-17. DOI:10.1016/j.cep.2017.12.017 |
| [26] |
BAI L, ZHAO S, FU Y, et al. Experimental study of mass transfer in water/ionic liquid microdroplet systems using micro-LIF technique[J]. Chemical Engineering Journal, 2016, 298: 281-290. DOI:10.1016/j.cej.2016.04.034 |
| [27] |
ZHAO Y, CHEN G, YUAN Q. Liquid-liquid two-phase flow patterns in a rectangular microchannel[J]. AIChE Journal, 2006, 52(12): 4052-4060. DOI:10.1002/aic.11029 |
| [28] |
PRAKASH R, KUMAR VERMA R, GHOSH S. Liquid-liquid mass transfer in a serpentine miniature geometry- effect on pressure drop[J]. Chemical Engineering Journal, 2019, 369: 489-497. DOI:10.1016/j.cej.2019.03.064 |
| [29] |
HARINGA C, DE JONG C, HOANG D, et al. Breakup of elongated droplets in microfluidic T-junctions[J]. Physical Review Fluids, 2019, 4(2): 024203. DOI:10.1103/PhysRevFluids.4.024203 |
| [30] |
LIU Y, ZHAO Q, YUE J, et al. Effect of mixing on mass transfer characterization in continuous slugs and dispersed droplets in biphasic slug flow microreactors[J]. Chemical Engineering Journal, 2021, 406: 126885. DOI:10.1016/j.cej.2020.126885 |
| [31] |
KOVALEV A V, YAGODNITSYNA A A, BILSKY A V. Flow hydrodynamics of immiscible liquids with low viscosity ratio in a rectangular microchannel with T-junction[J]. Chemical Engineering Journal, 2018, 352: 120-132. DOI:10.1016/j.cej.2018.07.013 |
| [32] |
TSAOULIDIS D, DORE V, ANGELI P, et al. Flow patterns and pressure drop of ionic liquid–water two-phase flows in microchannels[J]. International Journal of Multiphase Flow, 2013, 54: 1-10. DOI:10.1016/j.ijmultiphaseflow.2013.02.002 |
| [33] |
SUN X, ZHU C, FU T, et al. Dynamics of droplet breakup and formation of satellite droplets in a microfluidic T-junction[J]. Chemical Engineering Science, 2018, 188: 158-169. DOI:10.1016/j.ces.2018.05.027 |
| [34] |
COSTA A L R, GOMES A, CUNHA R L. Studies of droplets formation regime and actual flow rate of liquid-liquid flows in flow-focusing microfluidic devices[J]. Experimental Thermal and Fluid Science, 2017, 85: 167-175. |
| [35] |
ZHANG Q, LI H, ZHU C, et al. Micro-magnetofluidics of ferrofluid droplet formation in a T-junction[J]. Colloids and Surfaces A: Physicochemical and Engineering Aspects, 2018, 537: 572-579. |
| [36] |
FU T, WEI L, ZHU C, et al. Flow patterns of liquid–liquid two-phase flow in non-Newtonian fluids in rectangular microchannels[J]. Chemical Engineering and Processing: Process Intensification, 2015, 91: 114-120. |
| [37] |
张沁丹, 付涛涛, 朱春英, 等. 十字聚焦型微通道内弹状液滴在黏弹性流体中的生成与尺寸预测[J]. 化工学报, 2016, 67(2): 504-511. ZHANG Q D, FU T T, ZHU C Y, et al. Formation and size prediction of slug droplet in viscoelastic fluid in flow-focusing microchannel[J]. CIESC Journal, 2016, 67(2): 504-511. |




