2. 新疆大学 化工学院, 新疆 乌鲁木齐 830046;
3. 中国石油化工股份有限公司镇海炼化分公司, 浙江 宁波 315200
2. School of Chemical Engineering, Xinjiang University, Urumqi 830046, China;
3. Sinopec Zhenhai Refining and Chemical Company, Ningbo 315200, China
实现碳达峰、碳中和,是我国为应对气候变化、推动经济高质量转型做出的重大战略决策,以煤制油、煤制天然气、煤制烯烃、煤制乙二醇等为主的现代煤化工行业是碳减排的重点[1-2]。大型煤气化技术作为煤炭清洁高效转化的核心技术,其气化产物是煤化工过程的重要原料气。然而在生产过程中,气化炉易受操作参数波动性的影响,气化性能难以维持最优水平。因此,为保证气化炉稳定、高效地运行,对水煤浆气化炉操作参数进行分析及优化,对提高转化效率、降低煤炭单耗具有重要意义。
煤炭气化过程模拟是实现煤气化过程优化和智能化的基础。现阶段煤气化模型可以分为热力学平衡模型、计算流体力学(computational fluid dynamics,CFD)模型和分区模型。Dai等[3]基于Gibbs自由能最小化原则对加压粉煤气流床气化过程建立模型,模拟结果与工业数据基本一致。Labbafan等[4]基于欧拉-拉格朗日方法中描述的守恒方程式对德士古气流床气化炉进行了三维模拟,分析了氧煤体积流量比和煤浆质量分数对气化炉性能特征的影响,模拟结果吻合良好。Monaghan等[5]、Sahraei等[6]以CFD模型为基础将气化炉流场划分为射流膨胀区、回流区和出口流区,集成了热力学性质、化学反应、流体动力学、传热等多种子模型,建立气流床气化炉分区模型。分区模型可以很好地表达气化炉的反应机理且计算速度较快,本研究采用分区模型模拟气化炉气化过程。
气化炉运行易受不确定性参数的影响,如设计变量、控制变量、状态变量都可能出现波动或改变,一些学者对气化炉的过程不确定性和模型不确定性进行了研究。Shastri等[7]使用CFD模拟研究了煤组分对气化炉运行的影响,将CFD模拟结果与Aspen Plus中开发的近似气化炉模型的结果进行比较,以表征和量化气化炉运行的不确定性,由于CFD模型的计算成本,该研究仅使用了15个样本。Gel等[8]以挥发物各组分的质量分数以及总挥发物产量为响应目标,使用不确定性量化(UQ)方法,研究了温度、压力和加热速率的不确定性对煤挥发的化学反应动力学影响。研究表明,温度对煤脱挥发分产物产率有显著影响。Sahraei等[9]利用蒙特卡洛(Monte Carlo,MC)法研究了石油焦的挥发分含量、固体粒径、多相流射流角度和回流比存在不确定性的情况下气化炉分区模型关键输出的可变性,研究表明,合成气的转化率、峰值温度存在显著变化;而干基合成气的组成未受到明显影响。以上研究主要集中在分析原料性质不确定性和模型参数不确定性方面,但是缺乏对操作参数(煤浆体积流量、煤浆质量分数、氧气体积流量)不确定性的系统性研究。
本研究以镇海炼化水煤浆气化炉为研究对象,通过建立气化炉分区模型,研究操作参数不确定性对气化炉关键输出的影响,选定煤浆(CWS)体积流量、煤浆质量分数、氧气体积流量进行不确定性分析,量化操作参数的波动性转化为气化炉输出的不确定度。再结合多因素敏感性整体分析,比较输出对不同操作参数波动的敏感性。最后以气化炉操作温度作为约束,以不确定条件下的有效气产量作为优化目标进行随机最优化。
2 水煤浆气化炉反应器模型 2.1 建立模型水煤浆气化炉采用顶置四通道喷嘴,炉内气流的流动及相关反应过程随着气化炉高度和径向位置的不同而变化。水煤浆气化炉的流场测试结果表明[10],无因次长度0 < L < 3时,流场可分为射流区和回流区;当L≥3时呈管流流型。气化反应根据化学反应特征分为一次反应与二次反应,一次反应是可燃组分的燃烧反应,主要发生在射流区的火焰区域,以氧气耗尽为结束标志,其余区域发生二次反应,即一次反应产物的均相和非均相反应。结合气化炉中气相组分、碳转化率及温度在炉内的一维无因次分布结果对一次反应区进行划分[11],无因次长度的2% 处煤脱挥发分过程结束,无因次长度的3% 处燃烧过程结束。综合以上研究,气化炉按流场结构和化学反应特征可分为射流区、燃烧区、射流膨胀区、回流区和管流区。考虑到下降管中高温合成气与激冷水发生较快的变换反应对气化室出口合成气的气体组成影响显著,在分区中增加下降管区(Z6)[12]。结合以上研究,以水煤浆气化炉的分区结构为基础,利用Unisim搭建气化炉反应器网络模型,如图 1所示。
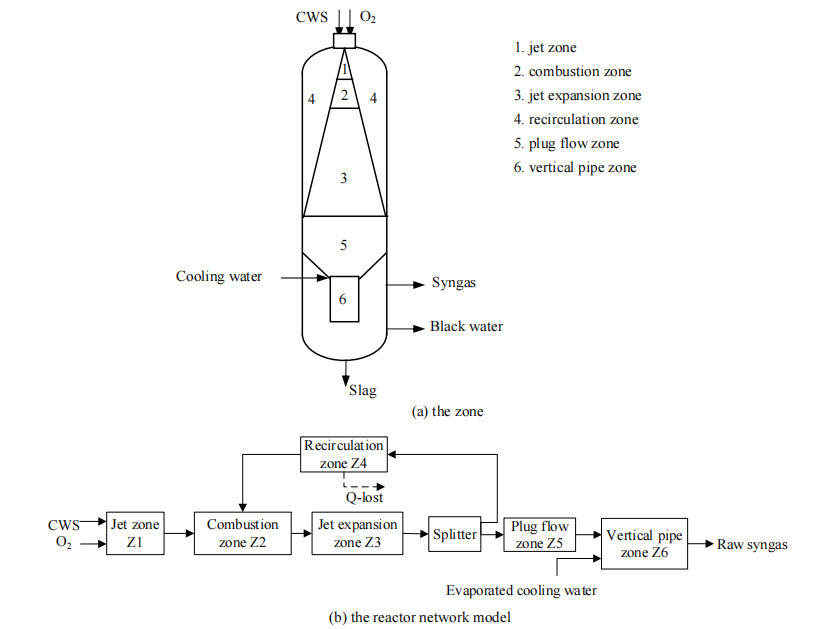
|
图 1 水煤浆气化炉分区及反应器网络模型 Fig.1 The zones and reactor model of CWS gasifier |
模型涉及的化学反应如式(1)~(13),依据流场结构和化学反应特征对气化炉各分区的化学反应和几何尺寸进行假设[13],大尺度的回流区可以实现煤焦颗粒的合理停留时间分布[14],各反应器对应的气化炉分区、几何尺寸及化学反应由表 1给出。气化炉在回流区的热损失设定为入炉煤低位热值的0.5%[15]。根据之前的研究,激冷水流量及温度在一定范围内对激冷室出口合成气组成影响不大,利用Fluent模拟下降管中激冷水的蒸发过程[12],计算得到参与反应的水蒸气质量流量为5 500 kg·h−1,占激冷水入口总质量流量的2.8%。设定分割器的分割比为0.8:0.2,即流股质量流率的80% 参与回流。
| $ \begin{gathered} 1{\rm{C}}{\rm{oal}} \to {\alpha _1}{\rm{C}} + {\alpha _2}{\rm{C}}{\rm{O}} + {\alpha _3}{\rm{C}}{{\rm{O}}_2} + {\alpha _4}{\rm{C}}{{\rm{H}}_4} + {\alpha _5}{{\rm{C}}_2}{{\rm{H}}_6} + {\alpha _6}{{\rm{C}}_6}{{\rm{H}}_6} + \\ {\alpha _7}{{\rm{H}}_2} + {\alpha _8}{{\rm{H}}_2}{\rm{O}} + {\alpha _9}{{\rm{H}}_2}{\rm{S}} + {\alpha _{10}}{\rm{N}}{{\rm{H}}_3} + {\alpha _{11}}{\rm{AS}}{\rm{H}} \\ \end{gathered} $ | (1) |
| $ {\rm{C}}{\rm{O}} + 0.5{{\rm{O}}_2} \to {\rm{C}}{{\rm{O}}_2} $ | (2) |
| $ {{\rm{H}}_2} + 0.5{{\rm{O}}_2} \to {{\rm{H}}_2}{\rm{O}} $ | (3) |
| $ {\rm{C}}{{\rm{H}}_4} + 2{{\rm{O}}_2} \to {\rm{C}}{{\rm{O}}_2} + 2{{\rm{H}}_2}{\rm{O}} $ | (4) |
| $ {{\rm{C}}_2}{{\rm{H}}_6} + 3.5{{\rm{O}}_2} \to 2{\rm{C}}{{\rm{O}}_2} + 3{{\rm{H}}_2}{\rm{O}} $ | (5) |
| $ {{\rm{C}}_6}{{\rm{H}}_6} + 7.5{{\rm{O}}_2} \to 6{\rm{C}}{{\rm{O}}_2} + 3{{\rm{H}}_2}{\rm{O}} $ | (6) |
| $ {\rm{C}}{\rm{O}} + {{\rm{H}}_2}{\rm{O}} \to {\rm{C}}{{\rm{O}}_2} + {{\rm{H}}_2} $ | (7) |
| $ {\rm{C}}{{\rm{H}}_4} + {{\rm{H}}_2}{\rm{O}} \to {\rm{C}}{\rm{O}} + 3{{\rm{H}}_2} $ | (8) |
| $ {\rm{C}}{\rm{O}}{\rm{S}} + {{\rm{H}}_2}{\rm{O}} \to {{\rm{H}}_2}{\rm{S}} + {\rm{C}}{{\rm{O}}_2} $ | (9) |
| $ 0.5{{\rm{N}}_2} + 1.5{{\rm{H}}_2} \to {\rm{N}}{{\rm{H}}_3} $ | (10) |
| $ {\rm{C}} + {{\rm{O}}_2} \to {\rm{C}}{{\rm{O}}_2} $ | (11) |
| $ {\rm{C}} + {{\rm{H}}_2}{\rm{O}} \to {\rm{C}}{\rm{O}} + {{\rm{H}}_2} $ | (12) |
| $ {\rm{C}} + {\rm{C}}{{\rm{O}}_2} \to 2{\rm{C}}{\rm{O}} $ | (13) |
|
|
表 1 气化炉各分区的几何尺寸和化学反应 Table 1 Geometric size and chemical reaction of each zone of gasifier |
气化炉射流区选用收率反应器模拟,式(1)热解产物的组分用Merrick法[16]计算,其余分区的反应均选用平推流反应器模拟。根据李超等[11]、杨俊宇等[17]对气流床通用网络模型的研究设定各平推流反应器内均相反应的动力学数据。式(11)、(12)及(13)为碳的非均相反应,反应速率采用随机孔模型计算[18],在Visual Basic中编写动力学参数后向Unisim中注册拓展子程序。
2.2 模型验证以镇海炼化水煤浆气化装置为基础收集工业数据,气化炉使用神府煤,煤质分析数据由表 2给出。从工业数据选择了3种工况,运用模型对气化结果进行预测,并将预测结果与工业数据进行比较,预测结果如表 3所示。
|
|
表 2 煤质分析 Table 2 Coal quality analysis |
|
|
表 3 模型结果检验 Table 3 Model result verification |
根据表 3结果,对3种工况关于气化结果的预测偏差取平均,模型对气化温度及CO、H2和CO2含量的预测误差为0.88%、2.05%、3.87% 和4.33%。预测结果与工业实测数据总体上保持一致,可将模型用于下一步水煤浆气化过程的模拟分析。
3 不确定性分析 3.1 操作参数不确定性量化采用MC法作为不确定性分析方法来研究气化炉稳定运行情况下操作参数的影响。MC法利用从不确定参数分布中随机选择的大量样本点和一个主要模型来传播不确定性,从而量化输出波动[9]。煤浆质量分数的数据为每12 h取样烘干称重的分析数据,case1操作参数随时间序列的分布如图 2所示。对图 2中的数据进行处理和正态分布拟合,结果如表 4所示。
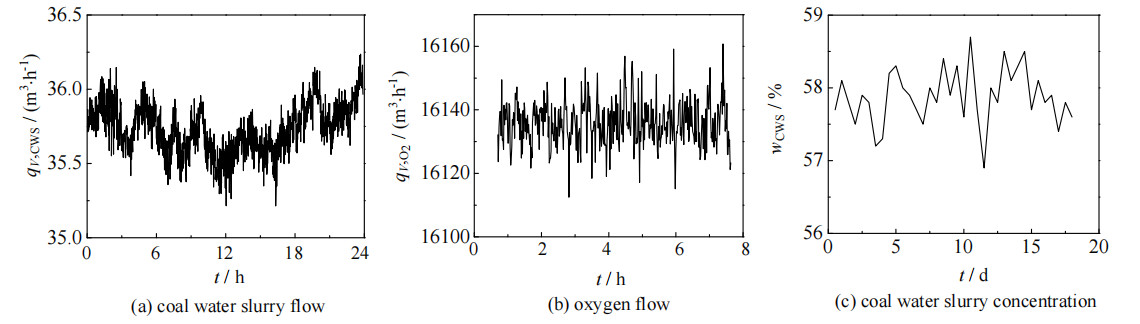
|
图 2 操作参数随时间序列的分布 Fig.2 Distribution of operating parameters with time |
|
|
表 4 操作参数的分布 Table 4 Operating parameters |
将输出不确定性表示为概率分布图,煤浆体积流量、氧气体积流量和煤浆质量分数的波动对实际运行中的气化炉温度和有效气产量分布的影响如图 3所示。
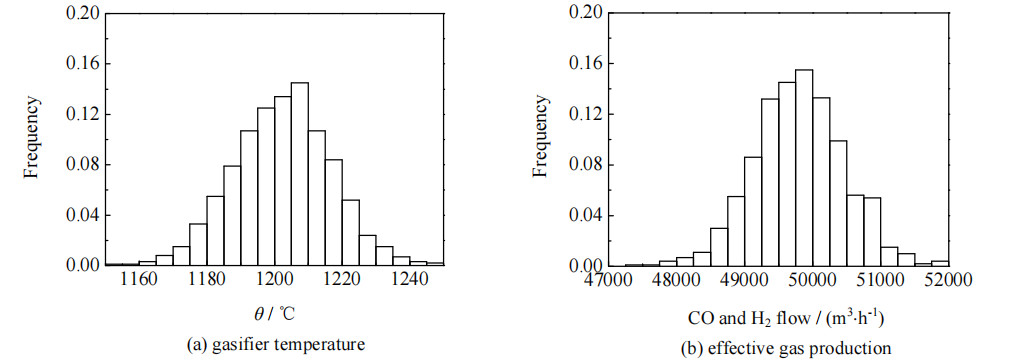
|
图 3 气化炉温度和有效气产量的概率分布图 Fig.3 Probability distribution of gasifier temperature and effective gas production |
参数的相对不确定度表示方法如式(14)所示,其中标准方差
| $ {u_{\rm{r}}} = \frac{{\sqrt V }}{\mu } \times 100\% $ | (14) |
经计算得出,操作参数的不确定度:煤浆体积流量为0.55%,氧气体积流量为0.06% 和煤浆质量分数为0.67%,转化为有效气产量分布为1.33%。有效气产量均值为49 799 m3·h−1,95% 置信区间,有效气产量在48 709 ~50 890 m3·h−1。操作参数转化为气化炉温度分布的不确定度为1.20%,均值为1 202 ℃,95% 的置信区间内气化炉操作温度在1 179~1 226 ℃。在气化炉运行时,为了保证出渣口的液态排渣,气化炉操作温度需高于煤灰流动温度θFT。该操作参数下气化炉基本可以运行,但操作温度离煤灰熔融温度非常接近。
3.2 操作参数敏感性整体分析工业上操作参数的波动性互相关联,共同影响气化炉温度和有效气产量的大小,需要进行多因素敏感性整体分析量化各因素对目标的影响。本研究在前文不确定性分析1 000组采样输出的基础上采用Spearman秩相关系数法进行操作参数不确定性的敏感性整体分析,即在氧气体积流量、煤浆体积流量和煤浆质量分数同时发生波动时,分析输出对各操作参数的敏感程度。Spearman秩相关系数是衡量参数依赖性的非参数指标,通过对比输入和对应目标响应的排行来分析各因素对目标的影响程度[19],计算式见式(15)。
| $ \rho = \frac{{\sum\nolimits_{i = 1}^N {({l_i} - \overline l )({m_i} - \overline m )} }}{{\sqrt {\sum\nolimits_{i = 1}^N {{{({l_i} - \overline l )}^2}\sum\nolimits_{i = 1}^N {{{({m_i} - \overline m )}^2}} } } }} $ | (15) |
Spearman秩相关系数的正负代表正负相关性,取绝对值后的大小则代表影响程度,操作参数的Spearman秩相关系数分析结果如表 5所示。
|
|
表 5 操作参数的Spearman秩相关系数 Table 5 Spearman rank correlation coefficient of operating parameters |
由Spearman秩相关系数分析可以得到气化炉运行时氧气流量的不确定性对输出的影响最小,可能是因为工业上氧气流量的波动性较小。煤浆体积流量的不确定性对温度的影响最大,其次是煤浆质量分数,呈负相关性。煤浆体积流量和煤浆质量分数对有效气产量的影响程度相近,且都呈正相关性。综合考虑2个关键输出,由敏感性整体分析可以得出煤浆体积流量的不确定性影响最大,其次是煤浆质量分数的不确定性,氧气体积流量的不确定性对输出的影响最小。
3.3 氧煤体积流量比优化在实际工业生产中,煤浆质量分数由煤种成浆性决定,煤浆体积流量取决于气化炉负荷的设计值,所以工业上一般通过监测氧气、煤浆的体积流量比来调节氧气体积流量进行气化炉控制。选取气化炉case1工况对氧气体积流量设定值进行优化。根据对神府煤黏温特性的研究,当θFT > 30 ℃时,灰渣黏度控制在25 Pa·s以下,符合液体排渣要求[20-21]。设定负荷下,选定有效气产量为优化目标,气化炉温度在1 190~1 400 ℃作为约束条件。选取均值表示有效气产量,调节氧煤体积流量比时,有效气产量与温度(95%置信度)的关系如图 4所示。
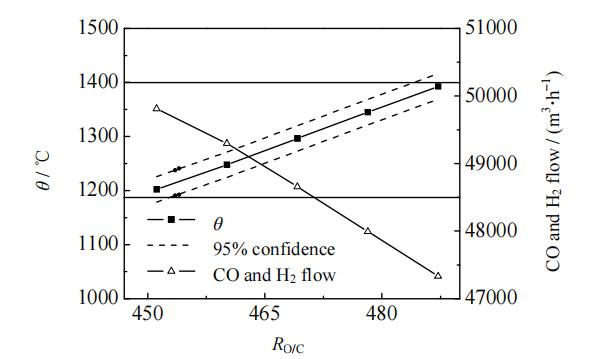
|
图 4 氧煤比对有效气产量与温度的影响 Fig.4 Effect of oxygen coal ratio on effective gas production and temperature |
由图 4可知当θ > 1 190 ℃时,温度和有效气产量呈现此消彼长的现象,不难得出,不考虑操作参数波动时,以实现气化炉的最大经济效益为目标,氧煤比的设定值容易设定偏低,在气化炉的运行过程中温度低于1 190 ℃的概率过高,易造成气化炉堵渣。为平衡产能目标和温度参数,在确定的最优化过程中加入随机模拟[22],根据操作参数分布基于MC法随机生成X组操作数据代入模型。在随机模拟过程中,需要对95% 置信区间的温度分布进行约束检查,在满足约束条件后继续进行目标函数值的计算。由图 4可以得出,95% 置信度下的温度下界越接近温度约束下界,目标函数值最大,此时的氧气体积流量为最优参数,优化过程中根据目标函数与约束的分布关系图设定合适的氧气体积流量初始值可以极大地降低计算量。
优化目标和机会约束条件由式(16)~
| $ \max {\text{ }}{\rm{CO}}{\text{ }}{\rm{and}}{\text{ }}{{\rm{H}}_2}{\text{ flow}} $ | (16) |
| $ {\rm{s.t.}}\text{ }P\left\{1\text{ }{190}_{} ^ \circ {\rm{C}}\le \theta \le 1\text{ }{400}_{}^ \circ {\rm{C}}\right\}\ge 95\% $ | (17) |
最优化结果:当氧气体积流量设置为16 221.7 m3·h−1时,温度均值为1 214.2 ℃,在95% 置信区间下,温度分布在1 190.8~1 237.5 ℃,有效气产量均值为49 680 m3·h−1,氧煤体积流量比分布在449.43~457.65,如图 5所示。优化操作参数后,在操作参数不确定的情况下,气化炉获得满足稳定运行要求的最优有效气产量。
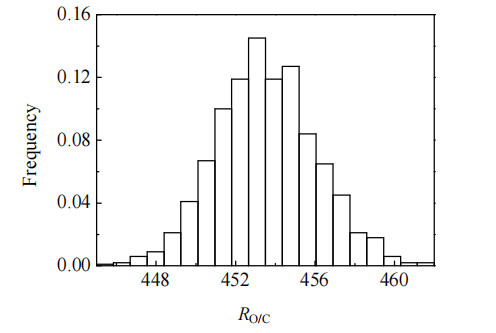
|
图 5 氧煤比的概率分布图 Fig.5 Probability distribution of oxygen coal ratio |
本研究采用气化炉分区模型对水煤浆气化炉进行建模,模拟结果与工业数据一致。采用蒙特卡洛法和Spearman秩相关系数法对操作参数进行不确定性分析和多因素敏感性整体分析。最后,以气化炉温度作为约束、以不确定条件下的有效气产量作为优化目标进行随机最优化。
(1) 不确定性分析量化了操作参数煤浆体积流量、氧气体积流量、煤浆质量分数的不确定性对气化炉温度和有效气产量的影响,操作参数不确定度为:煤浆体积流量0.55%,氧气体积流量0.06% 和煤浆质量分数0.67% 时,转化为有效气产量分布的不确定度为1.33%,转化为气化炉温度分布的不确定度为1.20%。并通过多因素敏感性整体分析法得到对输出影响最大的是煤浆体积流量的不确定性,影响最小的是氧气体积流量的不确定性。
(2) 探究了考虑操作参数不确定性时操作参数的优化方法。得到case1工况下最优化结果为设定氧气体积流量16 221.7 m3·h−1,此时温度在安全范围内波动,95% 置信区间下分布在1 190.8~1 237.5 ℃,氧煤体积流量比为449.43~457.65,有效气产量均值为49 680 m3·h−1。研究结果为气化炉操作参数最优性提供理论支撑。
符号说明:
ASH
—灰分
u
—标准不确定度,%
COS
—羰基硫
ur
—相对不确定度,%
FC
—固定碳
V
—方差
l
—样本输入的秩
VM
—挥发分
—l的均值
w
—质量分数
m
—目标响应的秩
wCWS
—煤浆质量分数,%
—m的均值
x
—摩尔分数
N
—样本个数
α1,α2…α11
—对应组分的化学计量数
QHHV
—高位发热量,kJ·kg−1
θ
—气化炉温度,℃
qV, O2
—标准状况下氧气体积流量,m3·h−1
θFT
—流动温度,℃
qV, CWS
—煤浆体积流量,m3·h−1
μ
—均值
RO/C
—氧煤体积流量比
ρ
—秩相关系数
t
—时间,h或d
| [1] |
孙旭东, 张博, 彭苏萍. 我国洁净煤技术2035发展趋势与战略对策研究[J]. 中国工程科学, 2020, 22(3): 132-140. SUN X D, ZHANG B, PENG S P. Development trend and strategic countermeasures of clean coal technology in China toward 2035[J]. Strategic Study of CAE, 2020, 22(3): 132-140. |
| [2] |
谢和平, 吴立新, 郑德志. 2025年中国能源消费及煤炭需求预测[J]. 煤炭学报, 2019, 44(7): 1949-1960. XIE H P, WU L X, ZHENG D Z. Prediction on the energy consumption and coal demand of China in 2025[J]. Journal of China Coal Society, 2019, 44(7): 1949-1960. DOI:10.13225/j.cnki.jccs.2019.0585 |
| [3] |
DAI Z H, GONG X, GUO X L, et al. Pilot-trial and modeling of a new type of pressurized entrained-flow pulverized coal gasification technology[J]. Fuel, 2008, 87(10/11): 2304-2313. |
| [4] |
LABBAFAN A, GHASSEMI H. Numerical modeling of an E-gas entrained flow gasifier to characterize a high-ash coal gasification[J]. Energy Conversion and Management, 2016, 112: 337-329. DOI:10.1016/j.enconman.2016.01.040 |
| [5] |
MONAGHAN R F D, GHONIEM A F. A dynamic reduced order model for simulating entrained flow gasifiers. Part Ⅱ: Model validation and sensitivity analysis[J]. Fuel, 2012, 94(1): 280-297. |
| [6] |
SAHRAEI M H, DUCHESNE M A, YANDON R, et al. Reduced order modeling of a short residence time gasifier[J]. Fuel, 2015, 161: 222-232. DOI:10.1016/j.fuel.2015.07.096 |
| [7] |
SHASTRI Y, DIWEKAR U. Stochastic modeling for uncertainty analysis and multiobjective optimization of IGCC system with single stage coal gasification[J]. Industrial & Engineering Chemistry Research, 2011, 50(9): 4879-4892. |
| [8] |
GEL A, CHAUDHARI K, TURTON R, et al. Application of uncertainty quantification methods for coal devolatilization kinetics in gasifier modeling[J]. Powder Technology, 2014, 265: 66-75. DOI:10.1016/j.powtec.2014.01.024 |
| [9] |
SAHRAEI M H, DUCHESNE M A, HUGHES R W, et al. Experimental assessment, model validation, and uncertainty quantification of a pilot-scale gasifier[J]. Industrial & Engineering Chemistry Research, 2016, 55(25): 6961-6970. |
| [10] |
于遵宏, 沈才大, 王辅臣, 等. 水煤浆气化炉气化过程的三区模型[J]. 燃料化学学报, 1993, 21(1): 90-95. YU Z H, SHEN C D, WANG F C, et al. Three-partition model for the gasification process of coal water slurry gasifier[J]. Journal of Fuel Chemistry and Technology, 1993, 21(1): 90-95. |
| [11] |
李超, 代正华, 孙钟华, 等. 气流床气化炉综合模型及颗粒粒径对气化结果的影响研究[J]. 高校化学工程学报, 2013, 27(4): 597-603. LI C, DAI Z H, SUN Z H, et al. Development of a comprehensive model of entrained flow coal gasifier and study of effects of particle diameter on gasification results[J]. Journal of Chemical Engineering of Chinese Universities, 2013, 27(4): 597-603. |
| [12] |
张强, 代正华, 黄波, 等. 水激冷对粉煤气化过程气体组成的影响[J]. 华东理工大学学报(自然科学版), 2018, 44(5): 625-630. ZHANG Q, DAI Z H, HUANG B, et al. Influence of water quench on syngas composition of entrained flow pulverized coal gasification process[J]. Journal of East China University of Science and Technology (Natural Science Edition), 2018, 44(5): 625-630. |
| [13] |
林慧丽, 代正华, 孙钟华, 等. 气流床气化炉气化过程的分区模拟[J]. 华东理工大学学报(自然科学版), 2012, 38(2): 142-148. LING H L, DAI Z H, SUN Z H, et al. Partition simulation for gasification process of entrained-flow gasifier[J]. Journal of East China University of Science and Technology (Natural Science Edition), 2012, 38(2): 142-148. |
| [14] |
SUN Z H, DAI Z H, ZHOU Z J, et al. Numerical simulation of industrial opposed multiburner coal water slurry entrained flow gasifier[J]. Industrial & Engineering Chemistry Research, 2012, 51(6): 2560-2569. |
| [15] |
张强, 孙峰, 代正华, 等. 水煤浆气化炉异常工况动态模拟研究[J]. 高校化学工程学报, 2017, 31(4): 856-862. ZHANG Q, SUN F, DAI Z H, et al. Dynamic simulation of coal water slurry gasifier under abnormal operation conditions[J]. Journal of Chemical Engineering of Chinese Universities, 2017, 31(4): 856-862. |
| [16] |
MERRICK D. Mathematical models of the thermal decomposition of coal[J]. Fuel, 1983, 62(5): 534-539. |
| [17] |
杨俊宇, 李超, 代正华, 等. 基于停留时间分布的气流床气化炉通用网络模型[J]. 华东理工大学学报(自然科学版), 2015, 41(3): 287-292, 402. YANG J Y, LI C, DAI Z H, et al. General network model based on the residence time distribution for entrained flow gasifier[J]. Journal of East China University of Science and Technology (Natural Science Edition), 2015, 41(3): 287-292, 402. |
| [18] |
BHATIA S K, PERLMUTTER D D. A random pore model for fluid-solid reactions: Ⅱ. Diffusion and transport effects[J]. AIChE Journal, 1981, 27(2): 247-254. |
| [19] |
曹渊, 韩峰, 王铁良, 等. 爆炸容器力学安全的敏感度分析方法[J]. 科技导报, 2013, 31(3): 28-32. CAO Y, HAN F, WANG T L, et al. Sensitive analysis of mechanical safety of explosion vessel[J]. Science & Technology Review, 2013, 31(3): 28-32. |
| [20] |
廖敏, 郭庆华, 梁钦锋, 等. 气化条件下煤灰高温物相变化及其对黏度的影响[J]. 中国电机工程学报, 2010, 30(17): 45-50. LIAO M, GUO Q H, LIANG Q F, et al. Phase transformation of coal ash at high temperature under gasification conditions and its' influence on viscosity[J]. Proceedings of the CSEE, 2010, 30(17): 45-50. |
| [21] |
沈中杰. 高温熔渣界面结晶及沉积颗粒反应机理[D]. 上海: 华东理工大学, 2017. SHEN Z J. Crystallization behavior and deposited particle reaction mechanism on the high temperature molten slag surface [D]. Shanghai: East China University of Science and Technology, 2017. |
| [22] |
牛腾, 尹洪超, 刘红, 等. 考虑多类型不确定性的蒸汽动力系统运行优化[J]. 高校化学工程学报, 2021, 35(1): 109-117. NIU T, YIN H C, LIU H, et al. Operational optimization of steam power systems considering multiple uncertainties[J]. Journal of Chemical Engineering of Chinese Universities, 2021, 35(1): 109-117. |




