随着现代自动化技术的快速发展,工业系统无论在规模、复杂程度还是在一体化程度上都在不断提高,但同时也造成故障发生概率不断增大,所以对控制精度和可靠性的要求也越来越高,人们迫切需要建立一个具有高性能的监控系统来监视系统的运行状态,实时检测出系统发生的故障[1-3]。近年来,基于数据驱动的故障检测技术在工业过程中得到了广泛应用,并成为了学术界的研究热点。
主元分析(principal component analysis, PCA) [4]方法已广泛应用于工业生产过程监视方面,但PCA提取原始数据的全局信息,丢失局部信息。因此,寻找保持原始数据局部结构的方法开始得到学术界的关注。HU等[5]将局部保持投影(locality preserving projections, LPP)算法运用于工业过程的统计监测中。通过离线和在线的比较,一定程度上显示了流形学习方法在故障检测中的优越性。但是投影向量不是正交的,增加了数据误差重构方面的难度。为了更好地保持数据的局部结构,CAI等[6]提出正交局部保持投影(orthogonal locality preserving projections, OLPP)算法,在LPP的基础上增加了一个正交化的约束条件,通过迭代计算得到相互正交的投影方向。在此基础上,GUO等[7]提出一种基于动态多向正交局部保持投影(dynamic multiway orthogonal locality preserving projections, DMOLPP)算法用于间歇过程故障检测,该算法将滑动窗口技术与OLPP相结合,能够在保持原始训练样本局部信息的同时降低数据误差重构方面的难度。LUO等[8]提出核全局-局部保持投影算法(kernel global-local preserving projections, KGLPP),将LPP算法推广应用于非线性生产过程,但KGLPP方法的检测效果受到核参数的影响。郭金玉等[9]提出集成核局部保持投影(ensemble kernel locality preserving projections, EKLPP)算法,解决KLPP方法的检测效果受到核参数影响的问题。为了提高LPP算法的故障检测性能,GUO等[10]提出差分局部保持投影(difference locality preserving projections, DLPP)算法,利用差分方法剔除数据的非线性和多模态结构,然后利用LPP进行故障检测。在此基础上,郭金玉等[11]提出一种基于统计差分局部保持投影(statistics difference locality preserving projections, SDLPP)的多模态间歇过程故障检测方法,利用统计模量分析和差分算法,使多模态数据变为单模态,保证数据近似服从高斯分布,从而达到提高LPP在多模态间歇过程中故障检测性能的目的。然而,这些局部算法不能有效地监控稀疏不一致的多模态过程。为了解决这个问题,本文尝试将二阶差商和LPP算法相结合,提出一种新的基于二阶差商局部保持投影(second order difference quotient locality preserving projections, SODQ-LPP)的多模态过程故障检测方法。通过二阶差商预处理算法消除多模态数据的多中心和稀疏不一致的特性,满足LPP算法的SPE和T2统计量要求数据服从高斯分布的需求,提高LPP算法在多模态数据中的检测效果。
2 基于二阶差商LPP的多模态过程故障检测 2.1 局部保持投影(LPP)方法LPP算法[12]是一种用于提取数据特征信息的降维方法,它可以很好地保留数据的局部信息,主要考虑的是保持数据中近邻点之间的结构。算法的核心是寻找转换矩阵A,使一系列的矩阵X = [x1, x2, …, xn]∈Rm×n投影到Y = [y1, y2, …, yn]∈Rl×n(l < < m)上,即yi = ATxi,使Y尽可能地代表X。其中m为变量数,n为样本数。LPP算法的目的是在降维的同时,保持样本固有的局部流形结构不变,是一种局部子空间学习算法。
通过求解优化式(1)的最小值问题求解矩阵A:
| $ \begin{array}{l} \alpha = \frac{1}{2}{\rm{argmin}}{\sum\limits_{i, j} {\left\| {{y_i} - {y_j}} \right\|} ^2}{W_i}_j\\ \;\;\; = \frac{1}{2}{\rm{argmin}}{\sum\limits_{i, j} {\left\| {{A^{\rm{T}}}{x_i} - {A^{\rm{T}}}{x_j}} \right\|} ^2}{W_i}_j\\ \;\;\; = {\rm{argmin}}{A^{\rm{T}}}XL{X^{\rm{T}}}A \end{array} $ | (1) |
约束条件是:
| $ {A^{\rm{T}}}XD{X^{\rm{T}}}A = 1 $ | (2) |
式中L是拉普拉斯矩阵,L = D -W,W是定义在数据点上的相似矩阵,
| $ {{W}_{ij}}=\left\{ \begin{align} & \text{exp}(-\left\| {{x}_{i}}-{{x}_{j}} \right\|/t),{{x}_{i}}是{{x}_{j}}的k近邻或{{x}_{j}}是{{x}_{i}}的k近邻 \\ & 0,qt \\ \end{align} \right. $ | (3) |
式中Wij是加权矩阵中的元素,参数t是根据经验设定的。求目标函数的最小值可以保证近邻点xi和xj的投影yi和yj也是近邻点。
| $ XL{X^{\rm{T}}}A = \lambda XD{X^{\rm{T}}}A $ | (4) |
其中,XLXT和XDXT都是对称且半正定的,因此求矩阵(XDXT)-1XLXT的最小特征值对应的特征向量,即得到投影矩阵A。
2.2 二阶差商预处理算法为消除数据的多模态特性,GUO等[10]运用差分算法即一阶差分算法对数据进行预处理,计算式为:
| $ {\rm{d}}x = {x_i} - {x_i}^* $ | (5) |
式中xi代表数据集X∈Rm×n中的第i (i= 1, 2,…,n)个样本,xi*是xi的最近邻样本,xi* 的选取是根据欧式距离d(xi, xi*)求得的。差分算法可以消除方差差异不明显的多模态特性,但对于模态间稀疏程度明显的多模态问题,差分算法就失去其有效性。
为了解决上述问题,消除各模态间的方差差异,ZHANG等[13]提出近邻差分算法,对于样本xi,先找到它的第k个近邻样本xik,进行一阶差分运算得到:
| $ {x^*} = {x_i} - {x_i}^k $ | (6) |
运用同样的方法,找到样本xik的第k个近邻样本xikk,再进行一阶差分运算得到:
| $ {{x}_{(k)}}^{*}={{x}_{i}}^{k}-{{x}_{i}}^{kk} $ | (7) |
一阶差分运算消除数据的多中心结构,同时能保持当前样本与其近邻之间的位置信息。为了描述数据的结构差异,定义样本xi的二阶差商如下:
| $ {{x}^{**}}=w[{{x}^{*}}-{{x}_{(k)}}^{*}] $ | (8) |
式中
下面对多模态数值例子进行预处理。假设有两个不同模态的数据,其中每个模态有800个样本。每个样本有两个变量,在每个模态中都是独立的。在模态1中,变量x1和x2均服从[-100, 1]的正态分布;在模态2中,变量x1和x2均服从[18,26]的正态分布。每个模态的400个正常数据作为训练样本,其余400个正常数据作为校验样本,6个异常数据作为故障样本。故障2、3和4是密集模态的故障,而故障1、5和6是稀疏模态的故障。图 1是训练样本、校验样本和故障样本的数据分布散点图。图中圆圈表示训练数据,星号表示校验数据,方块表示故障数据。从图 1可以看出,该数值例子是稀疏程度不同的多模态实例。
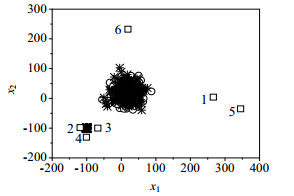
|
图 1 原始数据散点图 Fig.1 Scatter plot of original data |
通过寻优测试,在二阶差商算法中,样本的近邻数和近邻样本的近邻数k分别取为3和7。对多模态的数值例子运用差分和二阶差商的方法进行预处理,结果分别如图 2和图 3所示。图中圆圈表示训练数据,星号表示校验数据,方块表示故障数据。从图 2可以看出,差分算法可以剔除数据的多模态特性,使多模态数据变成单模态数据,有效地分离出靠近稀疏数据的故障1、5和6,但不能分离出靠近密集数据的故障2、3和4。这是由于差分算法能有效地处理方差差异小的多模态过程数据,而对于方差差异明显的多模态过程数据处理效果不理想。从图 3可以看出,二阶差商算法不但可以剔除数据的多模态特性,使多模态数据变成单模态数据,而且二阶差商算法可以有效地将所有故障数据分离出来。综上所述,二阶差商算法对于方差差异明显的多模态过程数据处理效果更好。经二阶差商方法预处理后,变量x1的分布如图 4所示。从图 4可以看出,预处理后数据服从高斯分布,满足LPP算法的SPE和T 2统计量要求数据服从高斯分布的需求。
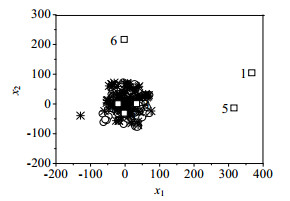
|
图 2 差分预处理散点图 Fig.2 Scatter plot of data preprocessed by difference algorithm |
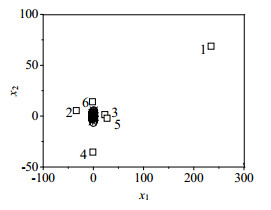
|
图 3 二阶差商预处理散点图 Fig.3 Scatter plot of data preprocessed by second order difference quotient |
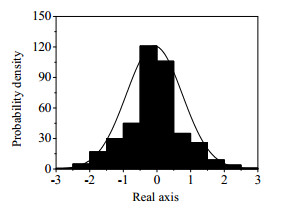
|
图 4 二阶差商预处理后变量x1的分布图 Fig.4 Distribution plot of variable x1 preprocessed by second order difference quotient |
采集正常工况下各个模态的数据,运用二阶差商进行预处理,从而消除多模态数据的多中心和方差差异特性,利用LPP方法建立模型,计算统计量并利用核密度估计法确定控制限。对新来的数据运用二阶差商预处理后,向LPP模型上进行投影,然后计算统计量并与控制限比较,从而进行多模态过程的故障检测。
基于二阶差商LPP的多模态过程故障检测流程如图 5所示。基于二阶差商LPP方法的多模态过程故障检测步骤主要分为建模过程和在线检测两部分。
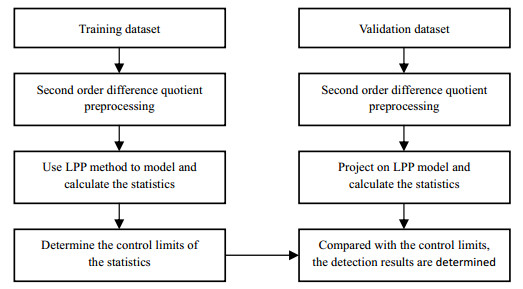
|
图 5 基于二阶差商LPP的多模态过程故障检测流程图 Fig.5 Fault detection flow chart of multimode processes based on second order difference quotient LPP |
(1) 建模过程
1) 对正常工况下各模态的训练数据运用二阶差商进行预处理得到矩阵X**,消除多模态数据的多中心和方差差异特性;
2) 确定加权矩阵W,利用式(4)求出投影矩阵A;
3) 运用LPP算法建立模型,并计算统计量SPE和T 2。SPE和T 2的计算公式为:
| $ \text{SPE}={{E}^{\text{T}}}E $ | (9) |
| $ {{T}^{2}}=T{{S}^{-1}}{{T}^{\text{T}}} $ | (10) |
其中T = A TX**,T为LPP降维后的主元矩阵,E = X**-AT,S是矩阵(X**DX**T)-1X**LX**T的l个最小特征值的对角阵;
4) 利用核密度估计法[14-16]确定统计量SPE和T 2的控制限。
(2) 在线检测
1) 对新来的校验数据运用二阶差商进行预处理;
2) 向LPP模型上进行投影,并计算统计量SPE和T 2;
3) 监控统计量SPE和T 2是否超过控制限。若统计量大于控制限,则该反应时刻的数据样本是故障的;否则是正常的。
3 仿真结果与分析 3.1 多模态数值例子通过寻优测试,在SODQ-LPP方法中,样本的近邻数和近邻样本的近邻数k分别取为3和7。对2.2节中的多模态数值例子运用LPP、DLPP和SODQ-LPP方法进行故障检测,检测结果如图 6所示。图中圆圈表示训练数据,星号表示校验数据,方块表示故障数据,虚线为95%控制限。从图 6可以看出,LPP算法的SPE和T 2统计量均有3个故障样本未检测出,38个样本出现误报。这是因为LPP方法不能有效地检测多模态过程数据。DLPP算法的SPE和T 2统计量均有3个故障样本未检测出,22个样本出现误报。这是由于DLPP方法能有效地检测方差差异小的多模态过程数据,而对于方差差异明显的多模态过程数据检测效果不理想。SODQ-LPP算法的SPE统计量检测出全部故障样本,18个样本出现误报;T 2统计量检测出全部故障样本,7个样本出现误报。与LPP和DLPP方法相比,SODQ-LPP故障检测率较高,误报率相对较低,从而验证SODQ-LPP方法的有效性。
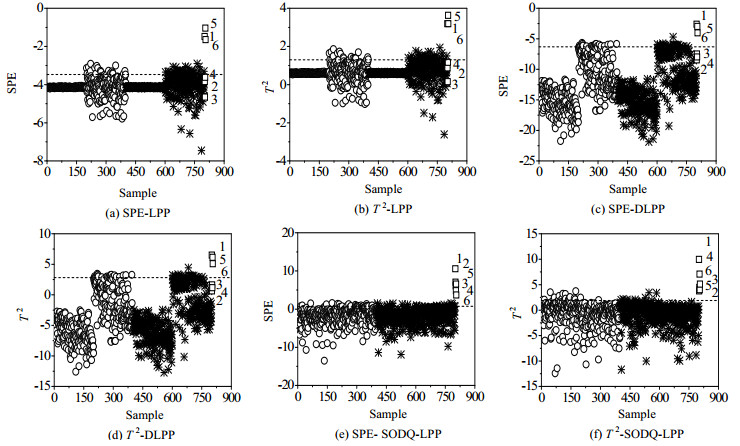
|
图 6 3种算法对多模态数值例子的检测结果图 Fig.6 Detection results of the three methods for multimodal numerical examples |
表 1是3种算法对多模态数值例子的检测结果对比。从表 1可以看出,SODQ-LPP方法的检测效果要明显优于LPP和DLPP方法。综上所述,与其它两种方法相比,SODQ-LPP方法有较低的误报率和漏报率,验证了该方法的有效性和优越性。
|
|
表 1 3种方法多模态数值例子的检测结果对比 Table 1 Comparison of detection results of the three methods for multimodal numerical examples |
半导体数据来源于美国德州仪器公司的半导体生产过程实际数据,是个典型的非线性、时变、多阶段和多工况的复杂多模态间歇过程。该数据由3个模态的107个正常批次和20个故障批次组成,其中1~34批次为第1模态,35~70批次为第2模态,71~107批次为第3模态。每个模态分别选取32个批次用于建模,其余的正常批次作为校验批次用于验证模型的准确性,因此建模批次为96个,正常校验批次为11个,故障批次为20个。本文从21个测量变量中选取17个变量作为检测变量,参见文献[17~20]。
每个批次是不等长的,持续时间在95~112 s变化。运用最短长度法获得等长批次。为了消除传感器中初始的波动影响,去除开始的5个样本,保留85个样本以适应最短的批次。将三维建模数据X(96×85×17)沿批次方向展开成二维矩阵X(96×1445)。对校验数据和故障数据也进行同样的处理。
通过寻优测试,在SODQ-LPP方法中,样本的近邻数和近邻样本的近邻数k分别取为13和27。对二维数据矩阵分别运用LPP、DLPP和SODQ-LPP方法进行建模,并对11个校验批次和20个故障批次数据进行检测。3种方法的检测结果如图 7所示,图中圆圈表示训练批次,星号表示校验批次,方块表示故障批次,虚线为95%控制限。从图 7中可以看出,LPP方法的SPE统计量有1个校验批次误报,故障批次有3个未检测出来;T 2统计量正确检测出全部校验批次,没有误报批次,但故障批次有13个未检测出来。LPP方法的检测效果不理想,这是因为LPP方法不能有效地检测多模态过程数据。DLPP方法的SPE统计量正确检测出全部校验批次,没有误报批次,而故障批次有2个未检测出来;T 2统计量正确检测出全部校验批次,没有误报批次,但故障批次有17个未检测出来。DLPP方法能有效地检测方差差异小的多模态过程数据,而对于方差差异明显的多模态过程数据,DLPP方法检测效果不理想。SODQ-LPP方法的SPE统计量正确检测出全部校验批次,没有误报批次,而故障批次有1个未检测出来;T 2统计量正确检测出全部校验批次,没有误报批次,但故障批次有12个未检测出来。与LPP和DLPP方法相比,SODQ-LPP方法的检测效果最好,验证了基于二阶差商LPP方法在多模态间歇过程故障检测中的有效性和优越性。
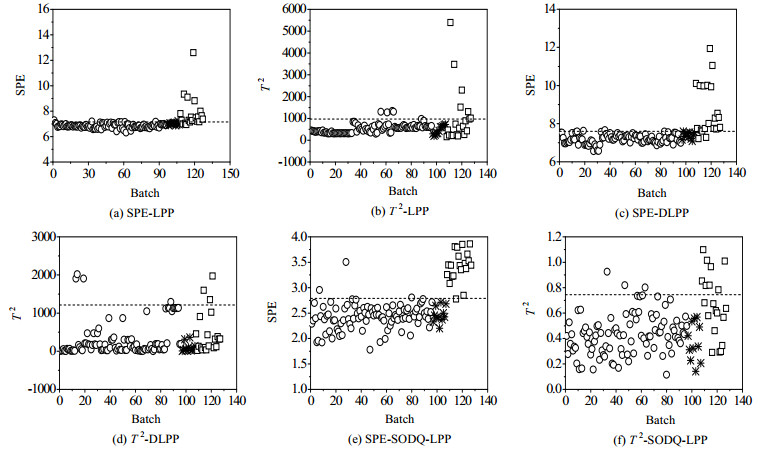
|
图 7 3种方法对半导体数据的检测结果图 Fig.7 Detection results of the three methods for semiconductor data |
表 2是3种方法对半导体数据的检测结果对比。由表 2可以看出,与LPP和DLPP方法相比,SODQ-LPP方法有较低的误报率和漏报率,说明该方法对于多模态数据的故障检测非常有效,从而验证了该方法的有效性和优越性。
|
|
表 2 3种方法对半导体数据的检测结果对比 Table 2 Comparison of detection results of the three methods for semiconductor data |
提出一种基于二阶差商LPP的多模态过程故障检测方法。该方法在进行多模态过程故障检测时,能够最大化地分离多模态的正常和故障数据。通过二阶差商预处理方法消除多模态数据的多中心和模态间的方差差异特性,从而更加准确地检测出故障数据。将提出的方法应用到数值例子和实际的半导体工业数据中,仿真结果表明,与传统的故障检测方法相比,本文的方法降低了误报率和漏报率,从而验证了该方法的有效性和优越性。
|
|
| [1] |
周东华, 李钢, 李元. 数据驱动的工业过程故障检测与诊断技术[M]. 北京: 科学出版社, 2011: 1-76. ZHOU D H, LI G, LI Y. Fault detection and diagnosis technology of industrial process based on data driven[M]. Beijing: Science Press, 2011: 1-76. |
| [2] |
张成, 郭青秀, 冯立伟, 等. 基于局部近邻标准化和动态主元分析的故障检测策略[J]. 计算机应用, 2018, 38(9): 2730-2734. ZHANG C, GUO Q X, FENG L W, et al. Fault detection strategy based on local neighbor standardization and dynamic principal component analysis[J]. Journal of Computer Applications, 2018, 38(9): 2730-2734. |
| [3] |
马贺贺, 胡益, 侍洪波. 基于距离空间统计量分析的多模态过程无监督故障检测[J]. CIESC Journal, 2012, 63(3): 873-880. MA H H, HU Y, SHI H B. Unsupervised fault detection for multimode processes using distance space statistics analysis[J]. CIESC Journal, 2012, 63(3): 873-880. DOI:10.3969/j.issn.0438-1157.2012.03.028 |
| [4] |
冯立伟, 徐涛. 基于局部近邻标准化和PCA的多工况过程故障检测方法研究[J]. 电脑知识与技术, 2017, 13(9): 214-216. FENG L W, XU T. Study on LNS-PCA-based fault detection method in multimode batch process[J]. Computer Knowledge and Technology, 2017, 13(9): 214-216. |
| [5] |
HU K, YUAN J. Multivariate statistical process control based on multiway locality preserving projections[J]. Journal of Process Control, 2008, 18(7): 797-807. |
| [6] |
CAI D, HE X, HAN J, et al. Orthogonal laplacianfaces for face recognition[J]. IEEE Transactions on Image Processing, 2006, 15(11): 3608-3614. DOI:10.1109/TIP.2006.881945 |
| [7] |
GUO J Y, QI L L, LI Y. Fault detection of batch process using dynamic multi-way orthogonal locality preserving projections[J]. Journal of Computational Information Systems, 2015, 11(2): 577-586. |
| [8] |
LUO L, BAO S, MAO J, et al. Nonlinear process monitoring based on kernel global-local preserving projections[J]. Journal of Process Control, 2016, 38: 11-21. DOI:10.1016/j.jprocont.2015.12.005 |
| [9] |
郭金玉, 王鑫, 李元. 基于集成核局部保持投影算法的故障检测[J]. 信息与控制, 2018, 47(2): 191-199. GUO J Y, WANG X, LI Y. Fault detection based on ensemble kernel locality preserving projections[J]. Information and Control, 2018, 47(2): 191-199. |
| [10] |
GUO J Y, ZHONG L L, LI Y. Fault detection based on difference locality preserving projections for the semiconductor process[J]. Journal of Chemometrics, 2018, 32(8): e3035. DOI:10.1002/cem.3035 |
| [11] |
郭金玉, 仲璐璐, 李元. 基于统计差分LPP的多模态间歇过程故障检测[J]. 计算机应用研究, 2019, 36(1): 123-126. GUO J Y, ZHONG L L, LI Y. Fault detection of multi-mode batch process based on statistics difference LPP[J]. Application Research of Computers, 2019, 36(1): 123-126. |
| [12] |
DENG S J, TANG L W, ZHANG X T. Research of adaptive neighborhood incremental principal component analysis and locality preserving projection manifold learning algorithm[J]. Journal of Shanghai Jiaotong University, 2018, 23(2): 269-275. DOI:10.1007/s12204-018-1936-7 |
| [13] |
ZHANG C, GAO X W, XU T, et al. Nearest neighbor difference rule-based kernel principal component analysis for fault detection in semiconductor manufacturing processes[J]. Journal of Chemometrics, 2017, 31(6): e2888. DOI:10.1002/cem.2888 |
| [14] |
杨宜东, 孙志挥, 张净. 基于核密度估计的分布数据流离群点检测[J]. 计算机研究与发展, 2005, 42(9): 1498-1504. YANG Y D, SUN Z H, ZHANG J. Finding outliers in distributed data streams based on kernel density estimation[J]. Journal of Computer Research and Development, 2005, 42(9): 1498-1504. |
| [15] |
ODIOWEI P P, CAO Y. Nonlinear dynamic process monitoring using canonical variate analysis and kernel density estimations[J]. IEEE Transactions on Industrial Informatics, 2010, 6(1): 36-45. DOI:10.1109/TII.2009.2032654 |
| [16] |
MORI J, YU J. Quality relevant nonlinear batch process performance monitoring using a kernel based multiway non-Gaussian latent subspace projection approach[J]. Journal of Process Control, 2014, 24(1): 57-71. DOI:10.1016/j.jprocont.2013.10.017 |
| [17] |
张成, 李元, 高宪文. 基于稀疏距离的间歇过程故障检测方法[J]. 信息与控制, 2014, 43(5): 588-595. ZHANG C, LI Y, GAO X W. Fault detection method for batch process based on sparse distance[J]. Information and Control, 2014, 43(5): 588-595. |
| [18] |
LEE S P, CHAO A K, TSUNG F, et al. Monitoring batch processes with multiple on-off steps in semiconductor manufacturing[J]. Journal of Quality Technology, 2011, 43(2): 142-157. DOI:10.1080/00224065.2011.11917852 |
| [19] |
WISE B M, GALLAGHER N B, BUTLER S W, et al. A comparison of principal component analysis, multiway principal component analysis, trilinear decomposition and parallel factor analysis for fault detection in a semiconductor etch process[J]. Journal of Chemometrics, 2015, 13(3/4): 379-396. |
| [20] |
GUO J Y, WANG X, LI Y, et al. Fault detection based on weighted difference principal component analysis[J]. Journal of Chemometrics, 2017, 31(11): e2926. DOI:10.1002/cem.2926 |




