气隙式膜蒸馏(air gap membrane distillation,AGMD)应用于海水淡化过程时,具有可使用低温热源、淡水回收率高且膜不易污染等优点[1],但是渗透通量低[2]的问题限制了其进一步工业应用。研究表明,在膜组件内部增设扰流结构[3-5]或通气[6-9]可增大料液扰动程度进而提高渗透通量。由于通气方法多样、气体流量可调,故通气强化方式更具应用前景[10]。实验证明,在适宜的通气条件下,通气强化过程膜蒸馏渗透通量可达到未通气情况时的1.72倍[7]。尽管进一步提高膜蒸馏渗透通量需要不断开发新技术,但对已有强化方法的深入研究可发掘其应用价值。以通气强化膜蒸馏方法为例,适宜的通气状态对强化效果至关重要。研究表明,小尺寸气泡对充分混合料液更有优势[6-7];不同通气条件所形成的气液流型对质量、热量传递过程的强化效果有差异[8];增大通入的气体流量和延长通气时间有利于缓解膜污染现象[9]。此外,在宏观实验的基础上采用计算流体动力学方法(computational fluid dynamics,CFD)定量探讨通气强化流动特性的研究报道也较丰富[11-15]。RADAEI等[11]的数值模拟结果表明通气可使剪应力增大5.3倍(0.04 Pa增至0.25 Pa);DU等[12]发现团状流的分离阻力只有泡状流的一半,但泡状流对料液的扰动作用大于团状流,并且团状流的膜壁剪应力为泡状流的10.7倍(团状流15 Pa、泡状流1.4 Pa);GUPTA等[13]通过合理设置壁面吸附参数(如接触角),观察到包裹气泡的薄层液膜,并定量分析了该层液膜对气泡及周围液相的影响;KESHAVARZI等[14]证明了大气泡对周围流体热量、质量传递过程的影响大于小气泡;RATKOVICH等[15]认为当气速明显大于液速时,膜壁剪应力分布更均匀。鉴于大部分通气模型数值模拟侧重于分析通入气体后气泡流动性质的变化,关于通气量对强化传质效果影响的定量关系仍不明晰。因此,本文将氮气引入气隙式膜蒸馏体系进行传质强化,并采用流体体积函数(volume of fluid,VOF)模型利用FLUENT软件对该强化过程进行CFD模拟,拟合出了实验条件下通气量(气含率)与强化传质效果(传质系数)的定量关系式,为多角度分析通气强化过程,深化对该强化方法的认识提供依据。
2 实验条件与模拟参数 2.1 实验条件自制疏水性管状煤基炭膜、仪器设备参数与课题组前期研究相同[16]。实验操作条件:NaCl溶液浓度3.5 g·L-1、入口温度60 ℃、流量40 L·h-1,冷却水入口温度20 ℃、流量120 L·h-1,常温氮气流量10~80 L·h-1。本文渗透通量数据引自课题组前期实验研究[16],用以检验所建模型及模拟方法的可靠性。
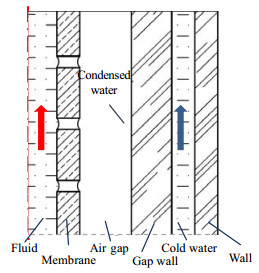
2.2 模拟参数图 1为气隙式膜蒸馏物理模型。氯化钠溶液与氮气以并流方式通入疏水多孔膜管,溶液中的淡水成分气化后透过膜孔移至气隙,最终在气隙壁冷凝并被收集。
|
图 1 气隙式膜蒸馏物理模型 Fig.1 Schematic diagram of AGMD |
图 2为利用GAMBIT软件、按照实际膜组件尺寸建立的二维计算域及网格划分示意图。经过网格无关性检验后,确定出较为适宜的网格尺寸分别为:膜管内腔0.500 0 mm×0.083 4 mm;膜管壁、气隙、料液及通气预混区0.5 mm×0.5 mm,计算域网格总数为20 677。

|
图 2 二维计算域结构化网格示意图 Fig.2 Schematic diagram of two dimensional computational domain with structured mesh |
利用FLUENT 6.3软件进行非稳态模拟,模拟参数见表 1。设置时间步长为10-6 s、迭代次数为104次,收敛残差为10-5。气液相间的表面张力因子设为0.072 N·m-1[17],多相流模型的库朗数设为0.25,将流体域中溶液气化吸收的热量以能量源项的形式添加至热量方程中。
|
|
表 1 模拟参数 Table 1 Simulation parameters |
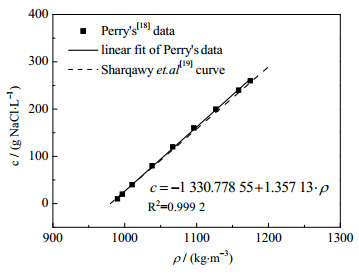
由于FLUENT软件需要输入的物性与输出的结果均为流体的密度值而非浓度值,因此需要根据文献中氯化钠溶液的浓度-密度数据[18]拟合关系式并进行换算,拟合结果见图 3。
|
图 3 氯化钠溶液浓度-密度关系式拟合结果 Fig.3 Correlation of concentration and density of sodium chloride solution |
模拟过程中,膜壁边界氯化钠溶液浓度的初值设为饱和浓度(368 g·L-1[20])。表 2列举了模拟过程涉及的流体与膜管物理参数,其中氯化钠溶液的比热容、热导率与黏度数据由文献的拟合式[19]计算而得。炭膜参数(φ,表示密度、比热容、热导率)由炭材料和水蒸气参数按式(1)[21]计算而得,计算式如下:
| $\varphi {\rm{m}} = \varphi {\rm{c}} \cdot (1 - \varepsilon ) + \varphi {\rm{v}} \cdot \varepsilon $ | (1) |
|
|
表 2 流体与膜管的物理参数(333 K) Table 2 Physical parameters of fluids and membrane tubes (333 K) |
初始条件如下:
| $ T{{|}_{t}}_{=0}={{T}_{0}},\ {{v}_{\text{l}}}{{|}_{t}}_{=0}={{v}_{l0}},\ {{v}_{\text{g}}}{{|}_{t}}_{=0}={{v}_{\text{g}0}},\ \alpha {{|}_{t}}_{=0}={{\alpha }_{0}},\ c{{|}_{t}}{{_{=0,r=2.5,r=}}_{-}}_{2.5}={{c}_{\text{sat}}} $ |
入口边界条件如下:
| $ T{|_z}_{ = 0} = {T_0}, \;{v_{\rm{l}}}{|_z}_{ = 0} = {v_{l0}}, \;{v_{\rm{g}}}{|_z}_{ = 0} = {v_{{\rm{g0}}}}, \;\alpha {|_z}_{ = 0} = {\alpha _0}, \;c{|_z}_{ = 0} = {c_0} $ |
出口边界条件如下:
| $ p{|_z}_{ = 100} = {p_{{\rm{amb}}}} $ |
壁面边界条件如下:
| $ v{{|}_{r}}{{_{=2.5,r=}}_{-}}_{2.5}=0,\ \gamma {{|}_{r}}{{_{=2.5,r=}}_{-}}_{2.5}={{125}^{°}} $ |
相界面边界条件如下:
| $ \beta = {\rm{ }}0.072{\rm{ N}} \cdot {{\rm{m}}^ - }^1 $ |
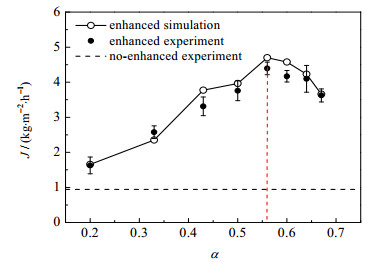
图 4为不同气含率(α)条件下的渗透通量实验值与模拟值对比结果。实验值为课题组前期实验结果[16],模拟值是通过对膜管内部流体进行热量衡算,结合模拟结果由式(2)计算而得。可以发现,模拟值与实验值趋势相似,大部分数据吻合较好;α增大时,渗透通量先增大后减小;当α=0.56时,渗透通量达到最大值;通气强化后的渗透通量均大于未通气的情况,说明通气能够对气隙式膜蒸馏传质过程起到强化作用。
| $ J = \frac{{{N_{\rm{l}}} \cdot ({H_{{\rm{l, i}}}} - {H_{{\rm{l, o}}}}) + N{\rm{g}} \cdot ({H_{{\rm{g, i}}}} - {H_{{\rm{g, o}}}}) - K \cdot A \cdot ({T_{{\rm{fm}}}} - {T_{{\rm{pm}}}})}}{{{H_{{\rm{vap}}}} - {H_{{\rm{l, o}}}}}} $ | (2) |
|
图 4 不同气含率条件下的渗透通量模拟与实验值对比 Fig.4 Comparison of simulative and experimental permeation results under different gas holdup values |
图 5所示为不同气含率条件下膜管内部氯化钠溶液浓度分布图。由图可直观观察到膜管内部浓度极化现象,即膜壁附近氯化钠浓度明显大于液相主体,但尚未达到实验条件下的饱和浓度(368 g·L-1)[20]的状态。因此在理论上不会出现在膜壁上析出氯化钠晶体的现象,在实验过程中也确实没有发现膜壁结晶现象。

|
图 5 不同气含率条件下氯化钠溶液浓度分布 Fig.5 Concentration distribution of sodium chloride under different gas holdup values |
此外,由于通入气体可对料液产生扰动作用,通气强化过程的浓度边界层并不具有像单相流体浓度边界层一样规则的形状。而膜管不同位置的浓度极化现象并不是均匀的,存在局部浓度明显偏大的位置,而该位置主要分布于几乎占据整个膜管截面的气团与膜壁间的液膜处。这是因为几乎要占据整个膜管截面的气团对液膜的挤压作用较大[17],加之液膜占据的流动空间较小,因此料液的循环流动受到较大限制,故局部浓度偏大。综上,可以认为两相流动过程的浓度分布形式与气相流动形态密切相关。
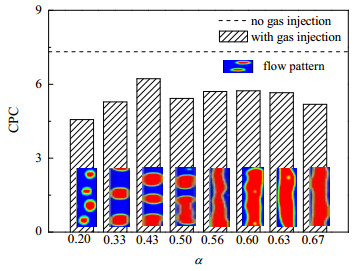
3.3 浓度极化率图 6所示为不同气含率条件下的浓度极化率(concentration polarization coefficient,CPC),计算式如下:
| $ CPC = \frac{{{c_{{\rm{fm}}}} - {c_{{\rm{pm}}}}}}{{{c_{\rm{f}}} - {c_{\rm{p}}}}} $ | (3) |
|
图 6 不同气含率条件下的浓度极化率 Fig.6 Concentration polarization coefficients under different gas holdup values |
可知,泡状流时(α≤0.33),CPC随着α增大而增大,这是因为小尺寸气泡对充分混合料液更有优势[6],因此小气泡可在一定程度上缓解浓度极化现象。当流型由泡状流过渡至塞状流时(α=0.33~0.43),CPC增大明显,这是因为泡状流对料液的扰动作用大于塞团状流[12],均匀分散的气泡更有利于减弱浓度极化现象。当气含率较大时(α≥0.50),CPC变化不大,说明当气相在膜管内以相对连续的状态较为稳定的流动时,通入的气体对料液的扰动作用差别不大,因此浓度极化程度的差异也不大;并且当气相的流动状态更加连续稳定时(α=0.67),浓度极化程度与CPC也相对更小。
3.4 传质系数关联式基于气体在多孔介质中的传质理论[22],结合通气强化过程的模拟结果可拟合出不同气含率条件下膜蒸馏传质系数(k)的关联计算式。
单相流体的膜蒸馏传质系数与渗透通量的关联计算式如下:
| $ J = k \cdot ({p_{{\rm{fm}}}} - {p_{{\rm{pm}}}}) $ | (4) |
气体在多孔介质中的传质机理,可分为分子扩散(Kn<0.01)、努森扩散(Kn>10)和过渡扩散(0.01<Kn<10) 3类,因此需要先计算研究体系的努森数(Kn)判断传质过程的控制机理,计算式如下:
| $ Kn = \frac{\lambda }{d} $ | (5) |
分子运动自由程λ按下式计算:
| $ \lambda = \frac{{{k_{\rm{B}}}T}}{{\sqrt 2 {\rm{ \mathsf{ π} }}p{{\rm{ \mathsf{ σ} }}^2}}} $ | (6) |
过渡扩散传质系数(kk-m)与努森扩散传质系数(kk)、分子扩散传质系数(km)均有关[22],如下:
| $ \frac{1}{{{k_{{\rm{k - m}}}}}} = \frac{1}{{{k_{\rm{k}}}}} + \frac{1}{{{k_{\rm{m}}}}} $ | (7) |
| $ {k_{\rm{k}}}{\rm{ = }}\frac{{\varepsilon d}}{{3\xi }}{(\frac{{8RT}}{{{\rm{ \mathsf{ π} }}M}})^{0.5}}\frac{M}{{RT\delta }} $ | (8) |
| $ {k_{\rm{m}}}{\rm{ = }}\frac{1}{{{p_a}}}\frac{\varepsilon }{{\xi \delta }}Dp\frac{M}{{RT}} $ | (9) |
式中,膜孔曲折因子(
| $ \xi {\rm{ = }}\frac{{{{(2 - \varepsilon )}^2}}}{\varepsilon } $ | (10) |
膜孔内空气压力(pa)的计算式如下:
| $ {p_{\rm{a}}}{\rm{ = }}p - {p_{\rm{v}}} $ | (11) |
式中,水蒸气饱和蒸气压(pv)采用安妥因方程计算:
| $ \ln {p_v} = A - \frac{B}{{T + C}} $ | (12) |
式中,A=23.196 4;B=3 816.44;C= -46.13[22]。经计算,333 K条件下pv=19 784.89 Pa。
扩散系数(D)与总压(p)的乘积可近似为温度的函数[22],关系式如下:
| $ Dp{\rm{ = }}1.89 \times {10^{ - 5}} \times {T^{2.072}} $ | (13) |
综上,与本文传质过程相关物理量的计算结果见表 3。
|
|
表 3 传质系数计算结果 Table 3 Calculation results of mass transfer coefficients |
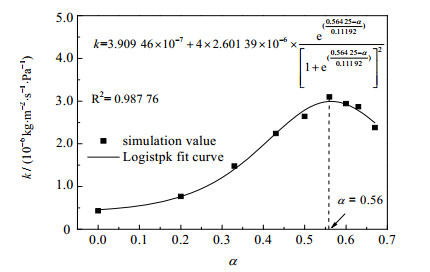
如图 7所示,式(14)为不同气含率条件下,根据模拟结果拟合出的传质系数关联式。
| $ k{\rm{ = }}3.909\;46 \times {10^{ - 7}} + 4 \times 2.601\;39 \times {10^{ - 6}} \times \frac{{{e^{( - z)}}}}{{{{\left[ {1 + {e^{( - z)}}} \right]}^2}}} $ | (14) |
|
图 7 不同气含率条件下的传质系数拟合曲线 Fig.7 Fitting curve of mass transfer coefficient under different gas holdup values |
其中:z是与气含率α相关的变量,计算式如下:
| $ z = \frac{{\alpha - 0.564\;25}}{{0.111\;92}} $ | (15) |
将式(14)改写为如式(16)通式形式:
| $ k{\rm{ = }}\frac{1}{{\frac{1}{{{k_{\rm{k}}}}} + \frac{1}{{{k_{\rm{m}}}}}}} + {k_v}({\alpha _{\max }}, \alpha ) + b $ | (16) |
| $ {k_v}\left( {{\alpha _{\max}}, \alpha } \right){\rm{ = }}\frac{{1.04 \times {{10}^{ - 5}} \times {e^{(\frac{{\alpha \max - \alpha }}{{0.11}})}}}}{{{{\left[ {1 + {e^{(\frac{{\alpha \max - \alpha }}{{0.11}})}}} \right]}^2}}} $ | (17) |
式中,αmax表示渗透通量最大时所对应的气含率(本文取实验结果0.56,参见图 4)。
从式(16)的结构上看,拟合出的通气强化过程膜蒸馏传质系数的计算式与气体在多孔介质中的过渡扩散机理对应传质系数[22]计算式的形式差异较大,这就说明单相流膜蒸馏的过渡扩散(Kn=0.9)传质机理不适用于通气强化过程。但是,其与过渡扩散-泊肃叶流传质系数计算式[23]的形式大体类似。可以说明,向膜管内通入气体可使单相流时在膜孔内以相对离散状态扩散的水蒸气分子以连续状态进行流动。因此,考虑了膜孔内气体分子连续流动效应的过渡扩散-泊肃叶流传质机理更接近于通气强化膜蒸馏过程的真实传质过程。
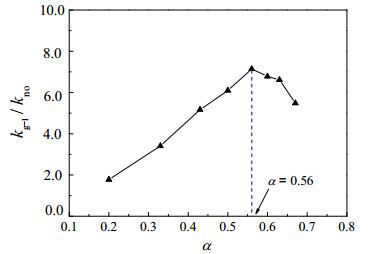
图 8所示为不同气含率条件下的强化与未强化过程传质系数之比。可知,通气强化过程的传质系数(kg-l)均大于未强化(kno)过程,当α=0.56时,kg-l约为kno的7倍,强化传质效果最好。故可认为并不是通入膜管的气体越多,强化传质效果越好。这是由于当气含率改变时,两相流型也会随之改变,因气相在膜管内的存在形态与气体含量对膜孔内水蒸气的扩散过程有极大的影响[7],不同气含率条件的传质系数差异较大。
|
图 8 不同气含率条件下的强化与未强化过程传质系数之比 Fig.8 Ratio of intensified to normal mass transfer coefficients under different gas holdup values |
采用VOF模型对通气强化气隙式膜蒸馏传质过程进行CFD模拟,得到如下结论:
(1) 不同气含率条件下,渗透通量、浓度分布形式与膜蒸馏传质系数存在较大差异。
(2) 浓度分布模拟结果可用于预测浓度极化程度,进而提出操作条件的改善方案;由拟合出的膜蒸馏传质系数关联式可知,考虑了孔内气体连续流动效应的过渡扩散-泊肃叶流传质机理更接近于通气强化膜蒸馏过程真实传质过程。
(3) 基于气体在多孔介质中的传质理论,通过合理建模并设定模拟参数,可研究通气强化传质过程的影响因素(本文为气含率)对强化效果的影响,该方法也可推广应用于分析多影响因素的膜蒸馏强化传质过程。
符号说明:
| A, B, C | —安妥因方程常数 | γ | —接触角,° |
| c | —浓度,kg NaCl·m-3 | δ | —膜厚,m |
| cp | —定压比热容,J·kg-1·K-1 | ε | —膜孔隙率 |
| D | —扩散系数,m2·s-1 | λ | —分子运动自由程,m |
| d | —膜平均孔径,m | μ | — 黏度,mPa·s |
| H | —焓,kJ·kg-1 | ρ | —密度,kg·m-3 |
| J | —渗透通量,kg·m-2·h-1 | σ | —水分子碰撞直径,4×10-10 m |
| K | —热导率,W·m-1·K-1 | φ | —膜管参数 |
| k | —传质系数,kg·m-2·s-1·Pa-1 | 下标 | |
| kB | —玻尔兹曼常数,1.38×10-26 kJ·K-1 | 0 | —初始态 |
| kg-l | —通气强化过程传质系数,kg·m-2·s-1·Pa-1 | a | —膜孔内空气 |
| kk | —努森扩散传质系数,kg·m-2·s-1·Pa-1 | amb | —大气 |
| kk-m | —过渡扩散传质系数,kg·m-2·s-1·Pa-1 | c | —炭材料 |
| km | —分子扩散传质系数,kg·m-2·s-1·Pa-1 | f | —进料侧 |
| kno | —无强化过程传质系数,kg·m-2·s-1·Pa-1 | g | —气相 |
| M | —水分子摩尔质量,18 kg·kmol-1 | i | —入口 |
| m | —质量,kg | l | —液相 |
| p | —压力,Pa | m | —膜 |
| R | —理想气体状态常数,8.31 m2·kg·s-2·K-1·mol-1 | o | —出口 |
| T | —温度,K | p | —渗透侧 |
| v | —速度,m·s-1 | sat | —饱和状态 |
| α | —气含率 | v | —水蒸气 |
| [1] |
BAGHBANZADEH M, RANA D, LAN C Q, et al. Zero thermal input membrane distillation, a zero-waste and sustainable solution for freshwater shortage[J]. Applied Energy, 2017, 187: 910-928. DOI:10.1016/j.apenergy.2016.10.142 |
| [2] |
CHO H, CHOI Y J, LEE S H. Effect of pretreatment and operating conditions on the performance of membrane distillation for the treatment of shale gas wastewater[J]. Desalination, 2018, 437: 195-209. DOI:10.1016/j.desal.2018.03.009 |
| [3] |
ALBEIRUTTY M, TURKMEN N, AL-SHARIF S, et al. An experimental study for the characterization of fluid dynamics and heat transport within the spacer-filled channels of membrane distillation modules[J]. Desalination, 2018, 430: 136-146. DOI:10.1016/j.desal.2017.12.043 |
| [4] |
LEE J G, JEONG S H, ALSAADI A S, et al. Influence of high range of mass transfer coefficient and convection heat transfer on direct contact membrane distillation performance[J]. Desalination, 2018, 426: 127-134. DOI:10.1016/j.desal.2017.10.034 |
| [5] |
HAGEDORN A, FIEG G, WINTER D, et al. Membrane and spacer evaluation with respect to future module design in membrane distillation[J]. Desalination, 2017, 413: 154-167. DOI:10.1016/j.desal.2017.03.016 |
| [6] |
CHEN G Z, YANG X, LU Y H, et al. Heat transfer intensification and scaling mitigation in bubbling-enhanced membrane distillation for brine concentration[J]. Journal of Membrane Science, 2014, 470: 60-69. DOI:10.1016/j.memsci.2014.07.017 |
| [7] |
CHEN G Z, YANG X, WANG R, et al. Performance enhancement and scaling control with gas bubbling in direct contact membrane distillation[J]. Desalination, 2013, 308(SI): 47-55. |
| [8] |
WU C R, JIA Y, CHEN H Y, et al. Study on air-bubbling strengthened membrane distillation process[J]. Desalination and Water Treatment, 2011, 34(1-3): 2-5. DOI:10.5004/dwt.2011.2785 |
| [9] |
DING Z W, LIU L Y, LIU Z, et al. The use of intermittent gas bubbling to control membrane fouling in concentrating TCM extract by membrane distillation[J]. Journal of Membrane Science, 2011, 372(1/2): 172-181. |
| [10] |
WIBISONO Y, CORNELISSEN E R, KEMPERMAN A J B, et al. Two-phase flow in membrane processes: A technology with a future[J]. Journal of Membrane Science, 2014, 453: 566-602. DOI:10.1016/j.memsci.2013.10.072 |
| [11] |
RADAEI E, LIU X F, TNG K H, et al. Insights on pulsed bubble control of membrane fouling: Effect of bubble size and frequency[J]. Journal of Membrane Science, 2018, 554: 59-70. DOI:10.1016/j.memsci.2018.02.058 |
| [12] |
DU X, LIU X F, WANG Y, et al. Particle deposition on flat sheet membranes under bubbly and slug flow aeration in coagulation-microfiltration process: Effects of particle characteristic and shear stress[J]. Journal of Membrane Science, 2018, 541: 668-676. |
| [13] |
GUPTA R, FLETCHER D F, HAYNES B S. On the CFD modelling of Taylor flow in microchannels[J]. Chemical Engineering Science, 2009, 64(12): 2941-2950. DOI:10.1016/j.ces.2009.03.018 |
| [14] |
KESHAVARZI G, PAWELL R S, BARBER T J, et al. Transient analysis of a single rising bubble used for numerical validation for multiphase flow[J]. Chemical Engineering Science, 2014, 112: 25-34. DOI:10.1016/j.ces.2014.02.027 |
| [15] |
RATKOVICH N, CHAN C C V, BERUBE P R, et al. Experimental study and CFD modelling of a two-phase slug flow for an airlift tubular membrane[J]. Chemical Engineering Science, 2009, 64(16): 3576-3584. DOI:10.1016/j.ces.2009.04.048 |
| [16] |
张金赫, 李花, 沈驭臣, 等. 膜蒸馏海水淡化过程中的两相流强化实验研究[J]. 高校化学工程学报, 2018, 32(1): 38-43. ZHANG J H, LI H, SHEN Y C, et al. Experimental Investigation on Two-Phase Flow Enhancement of Desalination Processes via Membrane Distillation[J]. Journal of Chemical Engineering of Chinese Universities, 2018, 32(1): 38-43. |
| [17] |
SAEED S L, ANDERS C O, SOREN K K. VOF modelling of gas-liquid flow in PEM water electrolysis cell micro-channels[J]. International Journal of Hydrogen Energy, 2017, 42(26): 16333-16344. DOI:10.1016/j.ijhydene.2017.05.079 |
| [18] |
PERRY R H, GREEN D W, MALONEY J O. Perry's chemical engineers' handbook 7th ed[M]. New York: McGraw-Hill, 1997.
|
| [19] |
SHARQAWY M H, LIENHARD V J H, ZUBAIR S M. Thermophysical properties of seawater: A review of existing correlations and data[J]. Desalination and Water Treatment, 2010, 16(1/2/3): 354-380. |
| [20] |
LANGER H, OFFERMANN H. On the solubility of sodium chloride in water[J]. Journal of Crystal Growth, 1982, 60(2): 389-392. |
| [21] |
YU H, YANG X, WANG R, et al. Numerical simulation of heat and mass transfer in direct membrane distillation in a hollow fiber module with laminar flow[J]. Journal of Membrane Science, 2011, 384(1/2): 107-116. |
| [22] |
CAI J C, GUO F. Study of mass transfer coefficient in membrane desalination[J]. Desalination, 2017, 407: 46-51. DOI:10.1016/j.desal.2016.12.013 |
| [23] |
DING Z W, MA R, FANEB A G. A new model for mass transfer in direct contact membrane distillation[J]. Desalination, 2003, 151(3): 217-227. DOI:10.1016/S0011-9164(02)01014-7 |




