众所周知,润湿性是固体表面的一个重要特性,是由固体表面的化学组成(或表面自由能)和表面几何构型(或表面粗糙度)共同决定的[1, 2]。近年来,一些特殊润湿性的表面,尤其是超疏水-超亲油或超亲水-超疏油表面,在油水分离等领域显示出诱人的应用前景,已成为国内外学者研究的热点[3~6]。大量研究表明,这种基于特殊润湿性表面的油水分离技术,主要取决于液体(油和水)在固体表面上的润湿性存在的巨大差异[7, 8]。因此,水或油在固体表面上的润湿性研究极为重要。对于纳米液滴而言,接触角的实验测定比较困难,但随着分子动力学(MD)模拟技术的出现,使纳米液滴接触角的确定已经成为可能。近几年,借助于分子动力学模拟,有关纳米液滴在纳米结构固体表面上的润湿特性的研究成果相继出现[9~13]。Hirvi等通过水滴在聚乙烯粗糙表面上接触角的MD模拟研究发现,在阵列高度相同的情况下,方柱截面较小的表面疏水性更强[9]。Yong等采用MD模拟方法,研究了纳米汞液滴在亲液性和疏液性纳米沟槽表面上的润湿特性,考察了粗糙度因子和相面积分数对接触角的影响规律[10]。Ambrosia等利用MD模拟技术,探讨了石墨阵列结构表面对纳米水滴接触角的影响,结果发现,随着阵列柱高度的增加,纳米液滴的接触角增大[11]。Chen等利用MD模拟方法,研究了纳米水滴在纳米阵列表面上存在的四种润湿模式,即Wenzel接触模式、亚稳定的Cassie接触模式、稳定的Cassie接触模式及混合润湿接触模式[12]。颜笑等人采用MD模拟研究了纳米水滴在纳米沟槽结构表面上的接触状态,考察了不同液-固相互作用强度下,纳米液滴的接触角和润湿模式随沟槽深度和沟槽宽度的变化规律[13]。本文拟采用分子动力学模拟技术,利用LAMMPS (Large-scale Atomic/Molecular Massively Parallel Simulator)软件,模拟研究纳米水滴在纳米粗糙壁面上的润湿行为,考察壁面形貌、粗糙度因子和相面积分数等因素对接触角的影响规律。
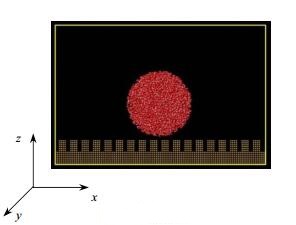
2 模拟方法 2.1 模拟体系的建立模拟体系的初始构型如图 1所示,模拟盒子尺寸为20 nm×20 nm×13 nm。4000个水分子随机分布成球形纳米液滴,水分子的初速度由随机数发生器确定[14]。纳米粗糙壁面采用铜原子参数,以FCC的方式排布,壁面原子数量与粗糙度因子或相面积分数大小有关。水液滴质心与壁面之间初始距离为3.4 nm。
|
图 1 初始构型 Fig.1 Initial configuration of simulation box |
水分子采用SPC/E刚体势能模型,其势能参数如表 1[15],总势能由短程L-J势能和长程静电势能两部分组成,如方程(1)所示[15]。
| 表 1 SPC/E模型的参数值 Table 1 Parameters of the SPC/E model |
| $U = {U_{{\rm{LJ}}}} + {U_{\rm{e}}} = \sum\limits_{i = 1}^N {\sum\limits_{j > i}^N {4{\varepsilon _{\rm{O}}}} } \left[ {{{\left( {\frac{{{\sigma _{\rm{O}}}}}{{r_{ij}^{{\rm{OO}}}}}} \right)}^{12}} - {{\left( {\frac{{{\sigma _{\rm{O}}}}}{{r_{ij}^{{\rm{OO}}}}}} \right)}^6}} \right] + {\rm{ }}\sum\limits_{i = 1}^N {\sum\limits_{j > 1}^N {\sum\limits_{A = 1}^n {\sum\limits_{B = 1}^n {\frac{{q_i^Aq_j^B}}{{4\pi {\varepsilon _{\rm{R}}}r_{ij}^{AB}}}} } } } {\rm{ }} $ | (1) |
水分子中O原子与壁面原子之间的相互作用,依然采用L-J的12-6势能形式,如式(2)所示,相应参数可以利用Lorentz-Berthelot混合规则确定,如方程(3)所示[15]。
| $ {U_{LJ}} = \sum\limits_{i = 1}^N {\sum\limits_{j > i}^N {4{\varepsilon _{{\rm{OS}}}}} } \left[ {{{\left( {\frac{{{\sigma _{{\rm{OS}}}}}}{{r_{ij}^{{\rm{OS}}}}}} \right)}^{12}} - {{\left( {\frac{{{\sigma _{{\rm{OS}}}}}}{{r_{ij}^{{\rm{OS}}}}}} \right)}^6}} \right]{\rm{ }} $ | (2) |
| $ {\varepsilon _{{\rm{OS}}}} = \sqrt {{\varepsilon _{\rm{O}}}{\varepsilon _{\rm{S}}}} , {\sigma _{{\rm{OS}}}} = \left( {{\sigma _{\rm{O}}} + {\sigma _{\rm{S}}}} \right)/2{\rm{ }} $ | (3) |
在进行分子动力学模拟过程中,x和y方向采用周期性边界条件,z方向采用固壁和镜像边界条件;原子间力的截断半径为1 nm,库伦力的截断半径为1.2 nm;模拟时间步长为1 fs,总模拟时间为2 ns,前1 ns使系统达到平衡,后1 ns统计计算并输出系统的密度分布。采用正则系综(NVT),并用Woodcock控温法维持体系温度衡定;每隔1000步矫正体系的质心。关于接触角的确定方法参见文献[15]。模拟数据采用LAMMPS软件计算得到。
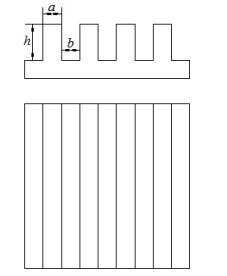
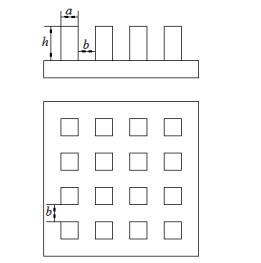
2.4 纳米粗糙壁面的构建本文构建的纳米栏栅形和纳米方柱矩阵形粗糙壁面的结构参数,分别如图 2和图 3所示。其中,凸起部分的宽度为a,凸起高度为h,凹陷部分的宽度为b。
|
图 2 纳米栏栅形粗糙壁面的结构参数示意图 Fig.2 Parameters of nanotextured fencing surface |
|
图 3 纳米方柱矩阵形粗糙壁面的结构参数示意图 Fig.3 Parameters of nanotextured square matrix surface |
纳米栏栅形和纳米方柱矩阵形粗糙壁面的粗糙度因子r与结构参数的关系,如式(4)和(5)所示[16];其相面积分数f与结构参数的关系,如方程(6)和(7)所示[16]。
| $r = 1 + \frac{{2h}}{{a + b}}{\rm{ }} $ | (4) |
| $r = 1 + \frac{{4ah}}{{{{(a + b)}^2}}} $ | (5) |
| $ f = \frac{a}{{a + b}} $ | (6) |
| $ f = \frac{{{a^2}}}{{{{(a + b)}^2}}} $ | (7) |
由方程(4)和(5)可见,当取a=b=h=2个晶格长度时,纳米栏栅形和纳米方柱矩阵形两种粗糙壁面的粗糙度因子相等(r=2)。
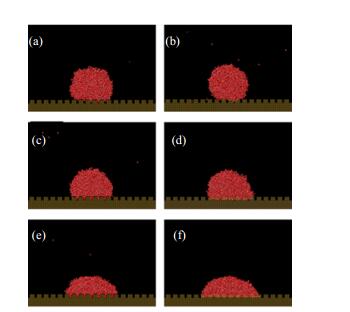
当模拟水分子数为4000,模拟温度为298 K,纳米栏栅形和纳米方柱矩阵形两种粗糙壁面的粗糙度因子都等于2时,在壁面作用势能分别为0.996(疏水壁面[15, 16])、1.674(中性壁面[15, 16])、3.347(亲水壁面[15, 16]) kJ·mol-1的条件下,采用分子动力学模拟技术,计算得到的纳米水滴在两种形貌壁面上的接触状态如图 4所示,其接触角变化如表 2所示,表 2中还与光滑壁面的MD模拟接触角θSS[15, 16]进行了比较。
|
图 4 壁面形貌对纳米水滴接触状态的影响 Fig.4 Effects of surface morphology on wetting status of water nanodroplets (a) fencing form, εS = 0.996 kJ·mol-1 (b) square matrix form, εS = 0.996 kJ·mol-1 (c) fencing form, εS = 1.674 kJ·mol-1 (d) square matrix form, εS = 1.674 kJ·mol-1 (e) fencing form, εS = 3.347 kJ·mol-1 (f) square matrix form, εS = 3.347 kJ·mol-1 |
| 表 2 壁面形貌对接触角θ的影响 Table 2 Effects of surface morphology on contact angels |
由表 2可见,当两种壁面的粗糙度因子相同时,纳米水滴在纳米栏栅形与在纳米方柱矩阵形粗糙壁面上的接触角相差不大。与光滑壁面的分子动力学模拟结果比较可见,对于亲水壁面,两种粗糙壁面的接触角要小于光滑壁面的,即粗糙壁面使亲水壁面更亲水;对于疏水壁面,两种粗糙壁面的接触角要大于光滑壁面的,即使疏水壁面更加疏水。
3.2 粗糙度因子的影响对于纳米栏栅形粗糙壁面,当取a=b时,由方程(6)计算得到,相面积分数f=0.5;在保持(a+b)=3个晶格长度的情况下,可以通过改变壁面凸起高度h的大小(h=1.5~4.5个晶格长度),来改变壁面粗糙度因子r的大小(r = 2~4)。
当模拟温度为298 K,模拟水分子数为4000,壁面粗糙度因子r = 2~4时,采用分子动力学模拟技术,探讨纳米水滴在壁面作用势能分别等于0.996(疏水壁面)、1.674(中性壁面)、3.347(亲水壁面) kJ·mol-1时的润湿行为。
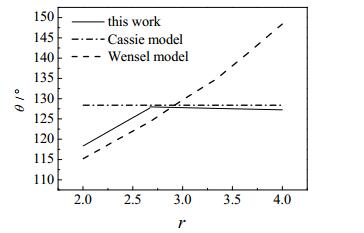
(1) 疏水壁面(εS= 0.996 kJ·mol-1)对于作用势能为0.996 kJ·mol-1的疏水壁面,当粗糙度因子r = 2~4时,纳米水滴的接触状态及接触角随粗糙度因子的变化分别如图 5和6所示,图 6中还与Wenzel接触角θW[16](可根据Wenzel方程(8)计算得到)及Cassie接触角θC[16](可根据Cassie方程(9)计算得到)进行了比较。

|
图 5 粗糙度因子对纳米水滴接触状态的影响 Fig.5 Effects of roughness factors on wetting status of water nanodroplets (εS = 0.996 kJ·mol-1) (a) r = 2 (b) r = 2.33 (c) r = 2.67 (d) r = 3 (e) r = 3.34 (f) r = 3.67 (g) r = 4 |
|
图 6 粗糙度因子对接触角的影响 Fig.6 Effects of roughness factors on contact angels (εS = 0.996 kJ·mol-1) |
| $\cos {\theta _{\rm{W}}} = r\cos \theta $ | (8) |
| $\cos {\theta _{\rm{C}}} = f\cos \theta + f - 1{\rm{ }} $ | (9) |
由图 6可见,当粗糙度因子较小(r<2.7)时,随着粗糙度因子(或壁面凸起高度)的增加,接触角不断增加,与Wenzel模型预测的结果比较接近,但比Wenzel模型得到的接触角稍大,这可能是由于纳米沟槽没有完全被水分子充满所致(参见图 5);当粗糙度因子到达2.7(联立方程(8)和(9)得到的理论值为2.85)以后,随着粗糙度因子(或壁面凸起高度)的进一步增大,接触角基本不变,与Cassie模型预测的结果比较一致,但比Cassie模型得到的接触角稍小一点,这可能是因为有少量水分子渗透到纳米沟槽内,导致复合接触出现“部分润湿”现象(参见图 5)。
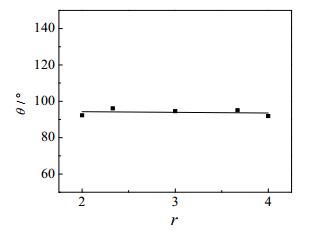
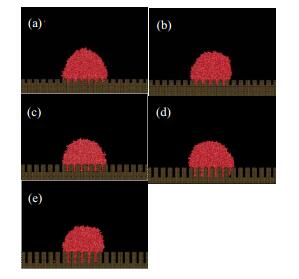
(2) 中性壁面(εS=1.674 kJ·mol-1)对于作用势能为1.674 kJ·mol-1的中性壁面,当粗糙度因子r=2~4时,纳米水滴的接触角随粗糙度因子的变化如图 7所示,可见,壁面粗糙度因子对接触角的影响不大。纳米水滴的接触状态如图 8所示,可见,对于中性粗糙壁面,纳米水滴为Wenzel接触模式。
|
图 7 粗糙度因子对接触角的影响 Fig.7 Effects of roughness factors on contact angels (εS = 1.674 kJ·mol-1) |
|
图 8 纳米水滴的接触状态 Fig.8 Effects of roughness factors on wetting status of water nanodroplets (εS=1.674 kJ·mol-1) (a) r= 2 (b) r = 2.33 (c) r = 3 (d) r = 3.67 (e) r = 4 |
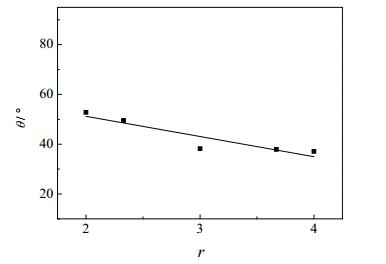
(3) 亲水壁面(εS=3.347 kJ·mol-1)对于作用势能为3.347 kJ·mol-1的亲水壁面,当粗糙度因子r = 2~4时,纳米水滴的接触角及接触状态随粗糙度因子的变化分别如图 9和10所示。
|
图 9 粗糙度因子对接触角的影响 Fig.9 Effects of roughness factors on contact angels (εS = 3.347 kJ·mol-1) |

|
图 10 粗糙度因子对润湿状态的影响 Fig.10 Effects of roughness factors on wetting states of water nanodroplets (εS = 3.347 kJ·mol-1) (a) r = 2 (b) r = 2.33 (c) r = 3 (d) r = 3.67 (e) r = 4 |
由图 9可见,对于亲水壁面,纳米液滴的接触角随粗糙度因子的增加而减小,即增大粗糙度使亲水壁面更亲水。由图 10可见,对于亲水性粗糙壁面,纳米水滴为Wenzel接触模式。
3.3 相面积分数的影响对于纳米栏栅形粗糙壁面,当取h=2.5个晶格长度,(a+b)=5个晶格长度时,由方程(4)计算得到,粗糙度因子r=2;可以通过改变壁面凸起宽度a的大小(a=1~4个晶格长度),来改变相面积分数f的大小(由方程(6)计算得到,f=0.2~0.8)。
当模拟温度为298 K,模拟水分子数为4000,相面积分数f=0.2~0.8时,采用分子动力学模拟技术,探讨纳米水滴在壁面作用势能分别等于0.996(疏水壁面)、1.674(中性壁面)、3.347(亲水壁面) kJ·mol-1时的润湿行为。
(1) 疏水壁面(εS= 0.996 kJ·mol-1)对于作用势能为0.996 kJ·mol-1的疏水壁面,当相面积分数f=0.2~0.8时,纳米水滴的润湿状态及接触角随相面积分数的变化分别如图 11和12所示,图 12中还与θW及θC[16]进行了比较。
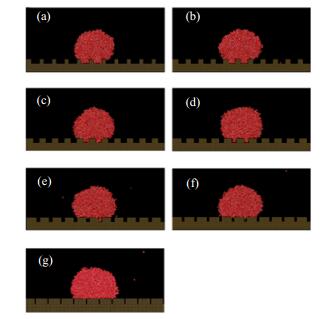
|
图 11 相面积分数对纳米水滴润湿状态的影响 Fig.11 Effects of phase area fractions on wetting status of water nanodroplets (εS =0.996 kJ·mol-1) (a)f = 0.2 (b) f = 0.3 (c) f = 0.4 (d) f = 0.5 (e) f = 0.6 (f) f = 0.7 (g) f = 0.8 |
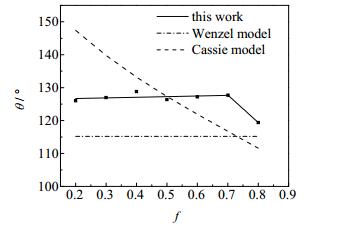
|
图 12 相面积分数对接触角的影响 Fig.12 Effects of phase area fractions on contact angels (εS =0.996 kJ·mol-1) |
由图 12可见,当f<0.7时,接触角基本等于常数,与相面积分数无关,与Wenzel模型预测结果的趋势基本一致,但模拟值偏大;当f>0.7时,随着相面积分数的进一步增大,接触角逐渐下降,与Cassie模型预测结果的趋势基本一致,但模拟值也偏大。通过对图 11的观察可以发现,这些纳米水滴的三相线几乎都处在沟槽峰面上(或外面),由于接触线的钉扎作用,限制了纳米液滴的向外铺展,从而形成了比Wenzel和Cassie理论值更大的模拟结果。总之,可以认为,对于纳米栏栅形疏水壁面,随着相面积分数的增加,接触角开始基本不变,后来逐渐下降。
(2) 中性壁面(εS=1.674 kJ·mol-1)对于作用势能为1.674 kJ·mol-1的中性壁面,当相面积分数f=0.2~0.7时,纳米水滴的接触角及润湿状态随相面积分数的变化分别如图 13和14所示。
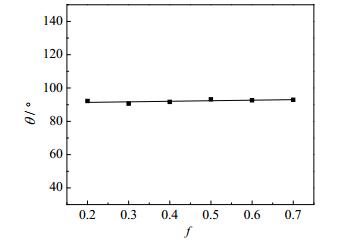
|
图 13 相面积分数对接触角的影响 Fig.13 Effects of phase area fractions on contact angels (εS =1.674 kJ·mol-1) |
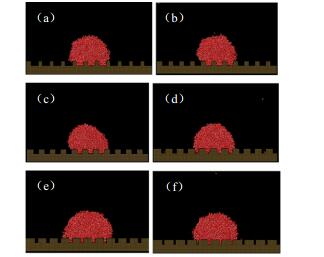
|
图 14 相面积分数对纳米水滴润湿状态的影响 Fig.14 Effects of phase area fractions on wetting states of water nanodroplets (εS = 1.674 kJ·mol-1) (a) f = 0.2 (b) f = 0.3 (c) f = 0.4 (d) f = 0.5 (e) f = 0.6 (f) f = 0.7 |
由图 13可知,对于中性壁面,随着相面积分数的增加,接触角变化不大。其润湿状态为图 14所示的Wenzel接触状态。
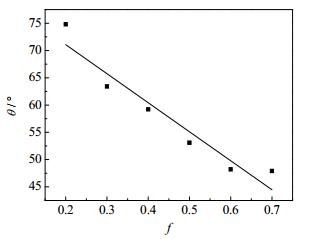
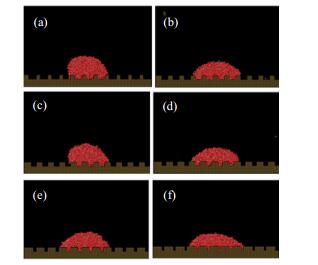
(3) 亲水壁面(εS= 3.347 kJ·mol-1)对于作用势能为3.347 kJ·mol-1的亲水壁面,当相面积分数f = 0.2~0.8时,纳米水滴的接触角及润湿状态随相面积分数的变化分别如图 15和16所示。由图 15可见,随着相面积分数的增大(即纳米缝隙的宽度减小),纳米水滴的接触角逐渐减小。由图 16可知,对于亲水性粗糙壁面,纳米水滴为Wenzel接触模式。
|
图 15 相面积分数对接触角的影响 Fig.15 Effects of phase area fractions on contact angels (εS =3.347 kJ·mol-1) |
|
图 16 相面积分数对纳米水滴润湿状态的影响 Fig.16 Effects of phase area fractions on wetting states of water nanodroplets (εS = 3.347 kJ·mol-1) (a) f = 0.2 (b) f = 0.3 (c) f = 0.4 (d) f = 0.5 (e) f = 0.6 (f) f = 0.7 |
本文采用分子动力学模拟技术,探讨了纳米水滴在纳米粗糙壁面上的润湿行为。考察了壁面形貌、粗糙度因子和相面积分数对接触角的影响规律,得到如下结论。
(1) 当壁面粗糙度因子相同时,纳米水滴在纳米栏栅形或纳米方柱矩阵形粗糙壁面上的接触角相差不大。
(2) 对于纳米栏栅形疏水壁面,随着粗糙度因子的增加,接触角开始不断增加,后来基本不变;随着相面积分数的增加,接触角开始基本不变,后来逐渐下降。
(3) 对于纳米栏栅形中性壁面,随着粗糙度因子或相面积分数的增加,纳米水滴的接触角变化不大,纳米水滴为Wenzel接触模式。
(4) 对于纳米栏栅形亲水壁面,纳米水滴的接触角随着粗糙度因子或相面积分数的增加而减小,即增大粗糙度因子或相面积分数,使亲水壁面更加亲水;纳米水滴为Wenzel接触模式。
| [1] | Xue C H, Ji P T, Zhang P, et al. Fabrication of superhydrophobic and superoleophilic textiles for oil-water separation[J]. Applied Surface Science , 2013, 284: 464-471. DOI:10.1016/j.apsusc.2013.07.120. |
| [2] | YU De-xu(于得旭), YU Zhi-jia(于志家), ZHAO Xiao-hang(赵小航), et al. Electrodepositing preparation and corrosion resistance studies of super-hydrophobic surface on copper substrate(铜基超疏水表面的电沉积法制备及其耐蚀性能研究)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报) , 2014, 28(5): 1178-11182. |
| [3] | YUAN Teng(袁腾), CHEN Zhuo(陈卓), ZHOU Xian-hong(周显宏), et al. Coated mesh film based on superhydrophilic and superoleophobic principle and its application in oil-water separation(基于超亲水超疏油原理的网膜及其在油水分离中的应用)[J]. Journal of Chemical Industry and Engineering (China)(化工学报) , 2014, 65(6): 1943-1951. |
| [4] | Feng L, Zhang Z Y, Mai Z h, et al. A super-hydrophobic and super-oleophilic coating mesh film for the separation of oil and water[J]. Angewandte Chemie-International Edition , 2004, 43(15): 2012-2014. DOI:10.1002/(ISSN)1521-3773. |
| [5] | ZHANG Liang(张靓), ZHAO Ning(赵宁), XU Jian(徐坚). Surfaces with special wettability:applications in oil/water separation(特殊浸润性表面在油水分离中的应用)[J]. Chinese Science Bulletin(科学通报) , 2013, 58(33): 3372-3380. |
| [6] | LI Jian(李坚), ZHANG Ming(张明), QIANG Tian-gang(强添刚). Research progress of the materials with special wettability for oil-water separation(特殊润湿性油水分离材料的研究进展)[J]. Journal of Forest and Environment(森林与环境学报) , 2016, 36(3): 257-265. |
| [7] | Su C H, Xu Y Q, Zhang W, et al. Porous ceramic membrane with superhydrophobic and superoleophilic surface for reclaiming oil from oily water[J]. Applied Surface Science , 2012, 258(7): 2319-2323. DOI:10.1016/j.apsusc.2011.10.005. |
| [8] | YU Zhi-jia(于志家), ZHAO Xiao-hang(赵小航), YU De-xu(于得旭), et al. Experimental research on demulsification and separation of emulsified oil-water mixture on composite hydrophobic mesh films(油水乳化液在复合疏水网膜上破乳与分离实验研究)[J]. Journal of Dalian University of Technology(大连理工大学学报) , 2015, 55(1): 1-6. DOI:10.7511/dllgxb201501001. |
| [9] | Hirvi T, Akkanen T A. Enhanced hydrophobicity of rough polymer surfaces[J]. The Journal of Physical Chemistry B , 2007, 111(13): 3336-3341. DOI:10.1021/jp067399j. |
| [10] | Yong X, Zhang L T. Nanoscale wetting on groove-patterned surfaces[J]. Langmuir , 2009, 25(9): 5045-5053. DOI:10.1021/la804025h. |
| [11] | Ambrosia M S, Ha M Y, Balachandar S. The effect of pillar surface fraction and pillar height on contact angles using molecular dynamics[J]. Applied Surface Science , 2013, 282: 211-216. DOI:10.1016/j.apsusc.2013.05.104. |
| [12] | Chen S A, Wang J D, Chen D R. States of a water droplet on nanostructured surfaces[J]. The Journal of Physical Chemistry C , 2014, 118(32): 18529-18536. DOI:10.1021/jp504070e. |
| [13] | YAN Xiao(颜笑), CHEN Feng(陈凤), ZHANG Qin-zhao(张勤昭), et al. Molecular dynamics simulations on wettability of nanogrooved surface(纳米沟槽表面润湿特性的分子动力学模拟)[J]. Atomic Energy Science and Technology(原子能科学技术) , 2015, 49(suppl): 342-348. |
| [14] | Heermann D W. Computer-simulation methods[M].Berlin: Springer Berlin Heidelberg, 1990. |
| [15] | WANG Tian(王甜), WANG Bao-he(王宝和). Wetting behavior of water droplets on smooth surfaces using molecular dynamics simulation(纳米水滴在光滑壁面上润湿行为的分子动力学模拟)[J]. Henan Chemical Industry(河南化工) , 2015, 2(1): 26-31. |
| [16] | WANG Tian (王甜). Wetting behaviors of sessile water nano-droplets using molecular dynamics simulation (固着纳米水滴润湿行为的分子动力学模拟) [D]. Dalian (大连): Dalian University of Technology (大连理工大学), 2015. http://cdmd.cnki.com.cn/Article/CDMD-10141-1015353083.htm |




