缠绕管式换热器具有单位容积换热面积大、换热系数高、传热温差小、换热效率高、耐高压、热膨胀自行补偿、不易结垢、易实现大型化的特点。在天然气液化、空气分离、低温工程等领域中获得了广泛的应用。因其结构的复杂性和特殊性,缠绕管式换热器的强化传热和流动机理的研究还不是很充分。因此,缠绕管式换热器强化传热和流动机理研究,具有巨大的理论价值和实用价值。
Moawed[1]通过实验研究了结构参数对缠绕管强制对流换的影响。Shokouhmand[2]、Salimpour[3]、Jamshidi[4]等分别通过实验,利用Wilson Plot方法得到管程与壳程的换热系数,得到了管程和壳程传热系数和压降的关联式,但是其适用范围极其有限。Gilli[5]根据横掠直管管束的关联式推导出缠绕管式换热器壳程的对流换热关联式;Schmidt[6]对缠绕管式换热器管程进行大量实验研究,拟合出了缠绕管式换热器管程的对流换热关联式,Gilli公式和Schmidt公式的适用化工领域的大部分工况。
大多数对流传热过程中存在两种有用能损失,流动阻力引起的有用能损失和温差传热引起的有用能损失。这两种有用能损失是不可逆的,因此,对流传热过程是典型的非平衡热力学过程。非平衡热力学说明,如果使得一个系统的有用能损失最小,那么必须使这个系统中的熵产最小。将对流传热过程中的熵产最小化,一直是学者们研究的重点和难点。Bejan[7-9]首先提出用熵理论(entropy theory)来描述传热过程,提出EGM方法(传热过程的“最小熵产原理”)。
缠绕管式换热器管程的非平衡热力学研究的方法,即为,使缠绕管式换热器管程的有用能损失最小,必须将缠绕管式换热器管程的熵产最小化。在Bejan研究的基础上,Shokouhmand[10]将EGM方法应用到圆形截面缠绕管的管内层流的强制对流换热的研究中,其边界条件是恒温壁面。Satapathy[11]对单根缠绕管式换热器的层流和湍流状态下的关联式和熵产率方程进行了耦合计算,然而,所选用的层流模型和湍流模型应用的范围非常有限。基于应用范围广泛的Gilli公式和Schmidt公式,学者们只是对缠绕管式换热器的设计计算方法进行了研究。尹接喜等[12]建立了缠绕管并管的传热计算模型,并提出了氢气回收装置中的缠绕管式换热器设计计算模型。陈永东等[13-14]建立了缠绕管式换热器在LNG工艺和煤化工的工艺中的设计准则,计算模型和热物性的计算方法。公茂琼等[15]编写了小型LNG系统的缠绕管换热器设计程序。徐成良[16]提出了缠绕管式换热器换热面积的一种简便计算方法。张周卫等[17-18]将逆流缠绕管式换热器和多股流缠绕管式换热器的设计计算模型进行程序化设计,并且对缠绕管式换热器在甲醇用系列冷却系统和液氮冷却系统中的应用进行了研究。
综上所述,在缠绕管式换热器管程的设计中,Schmidt公式的应用非常广泛。然而,基于Schmidt公式的缠绕管式换热器管程的非平衡热力学的研究却很少。因此,本研究以Schmidt公式的管程对流传热数学模型为基础,将其与非平衡热力学理论相结合,对缠绕管式换热器对流传热机理的研究,建立缠绕管式换热器管程的非平衡热力学热力学模型,具有重要的理论价值。
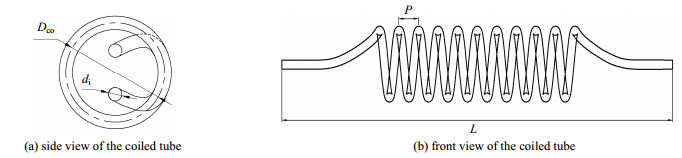
2 缠绕管式换热器管程对流传热的Schmidt数学模型Schmidt拟合了缠绕管(如图 1所示)的实验关联式,定义缠绕管内部流动的临界雷诺数为[6]:
| $ R{e_{{\rm{cr}}}} = 2300\left( {1 + 8.6{\delta ^{0.45}}} \right) $ | (1) |
|
图 1 缠绕管的结构示意图 Fig.1 Schematic diagram of the coiled tube structure |
式中,δ = di/Dco;其中di为缠绕管内径,Dco为缠绕管的缠绕直径。缠绕管内部流动的临界雷诺数Recr是区分缠绕管内部流动状态的标志。
Schmidt将缠绕管内部流动的Re分为三个区域。各区域强化传热和流动阻力系数的关联式为[6]
(1) 100 ≤ Re ≤ Recr
| $ Nu=3.65+0.08\left( 1+0.8{{\delta }^{0.9}} \right)R{{e}^{\left( 0.5+0.2903{{\delta }^{0.194}} \right)}}P{{r}^{1/3}} $ | (2) |
| $ f = \left( {1 + 0.14{\delta ^{0.97}}R{e^{\left( {1-0.664{\delta ^{0.312}}} \right)}}} \right)\frac{{64}}{{Re}} $ | (3) |
(2) Recr ≤ Re ≤ 22000
| $ Nu = 0.023\left[{1 + 14.8\left( {1 + \delta } \right){\delta ^{1/3}}} \right]R{e^{0.8 -0.22{\delta ^{0.1}}}}P{r^{1/3}} $ | (4) |
| $ f = \left( {1 + \frac{{28800{\delta ^{0.02}}}}{{Re}}} \right)\frac{{0.3164}}{{R{e^{0.25}}}} $ | (5) |
(3) 20000 ≤Re ≤ 150000
| $ Nu = 0.023\left[{1 + 3.6\left( {1-\delta } \right){\delta ^{0.8}}} \right]R{e^{0.8}}P{r^{1/3}} $ | (6) |
| $ f = \left[{1 + 0.0823\left( {1 + \delta } \right){\delta ^{0.58}}R{e^{0.25}}} \right]\frac{{0.3164}}{{R{e^{0.25}}}} $ | (7) |
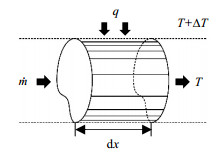
管道内部流动如图 2所示,根据非平衡热力学中熵产的定义,得到管道内部流动熵产为[19]
| $ {S_{{\rm{gen}}}} = \dot m\left( {{\rm{d}}h/{\rm{d}}x} \right)-q/\left( {T + \Delta T} \right) $ | (8) |
|
图 2 内部流动示意图 Fig.2 Schematic diagram of internal flow |
存在加热(或冷却)的管道内部流动属于无输出功的开口系统,此系统的热力学关系式为[20]
| $ \dot m\left( {{\rm{d}}h/{\rm{d}}x} \right) = q, \;\;\;{\rm{d}}h = T{\rm{d}}s + v{\rm{d}}p, \;\;\;v = 1/\rho $ | (9) |
将式(9)代入式(8),得到熵产的表达式为
| $ {S_{{\rm{gen}}}} = \frac{{q\Delta T}}{{T\left( {T + \Delta T} \right)}}-\frac{{\dot m}}{{\rho T}}\frac{{{\rm{d}}p}}{{{\rm{d}}x}} $ | (10) |
管道内部流动的Darcy阻力系数f和斯坦顿数St的数学表达式为[21]
| $ f =-\frac{{De}}{{2\rho {u^2}}}\frac{{{\rm{d}}p}}{{{\rm{d}}x}}, \;\;St = \frac{{q/\left( {\Omega \Delta T} \right)}}{{{c_{\rm{p}}}\dot m/A}} $ | (11) |
将式(11)代入式(10),可得
| $ {S_{\rm{gen}}} = \frac{{{q^2}}}{{4{T^2}\dot m{c_p}\left( {T + \Delta T} \right)}}\frac{{De}}{{St}} + \frac{{2{{\dot m}^3}}}{{{\rho ^2}T}}\frac{f}{{De{A^2}}} $ | (12) |
缠绕管的截面一般为圆管,根据圆管的结构关系(De = di,
| $ {S_{\rm{gen}}} = \frac{{{q^2}}}{{\pi \lambda {T^2}}} \cdot \frac{1}{{Nu}} + \frac{{32{{\dot m}^3}}}{{{\pi ^2}{\rho ^2}Td_{\rm{i}}^5}} \cdot f $ | (13) |
将内部流动非平衡热力学模型同Schmidt公式相结合,建立缠绕管式换热器管程对流传热的非平衡热力学的理论模型。首先,将式(13)进行无量纲化,引入无量纲化因子:
| $ {\mathit{\Phi}} = \frac{q}{{\lambda T}}, \;\;\;Re = \frac{{4\dot m}}{{\pi \mu {d_i}}}, \;\;B_0^2 = \frac{{{{\left( {\rho \dot mq} \right)}^2}}}{{\lambda T{\mu ^5}}} = \frac{{{{\left( {Req\rho \pi d} \right)}^2}}}{{16 \cdot \lambda T{\mu ^5}}} $ | (14) |
其次,引入截面为圆形的缠绕管内部流动的“熵产数”[19] (Ns,Ns = Sgen/λΦ2)。其数学表达式为
| $ {N_{\rm{s}}} = \frac{1}{\pi } \cdot \frac{1}{{Nu}} + \frac{{{\pi ^3}}}{{32}} \cdot \frac{{R{e^5}}}{{B_0^2}} \cdot f $ | (15) |
结合对流传热过程的不可逆损失的特点,将管道内部对流传热的不可逆损失分为两部分,传热不可逆损失和阻力不可逆损失。对应的无量纲熵产数分别为传热熵产数Ns, HX和阻力熵产数Ns, P,根据式(15),传热熵产数Ns, HX和阻力熵产数Ns, P的数学表达式为
| $ {N_{\rm{s, HX}}} = \frac{1}{\pi } \cdot \frac{1}{{Nu}} $ | (16) |
| $ {N_{\rm{s, P}}} = \frac{{{\pi ^3}}}{{32}} \cdot \frac{{R{e^5}}}{{B_0^2}} \cdot f $ | (17) |
将式(2)~(7)代入式(16)~(17),得到基于Schmidt公式的缠绕管式换热器管程对流传热的非平衡热力学理论模型的数学表达式:
(1) 100 ≤ Re ≤ Recr
| $ {N_{\rm{s, HX}}} = {\pi ^{- 1}} \cdot {\left[{3.65 + 0.08\left( {1 + 0.8{\delta ^{0.9}}} \right)R{e^{\left( {0.5 + 0.2903{\delta ^{0.194}}} \right)}}P{r^{1/3}}} \right]^{ -1}} $ | (18) |
| $ {N_{\rm{s, P}}} = \frac{{{\pi ^3}}}{{32}} \cdot \frac{{R{e^5}}}{{B_0^2}} \cdot \left[{\left( {1 + 0.14{\delta ^{0.97}}R{e^{\left( {1-0.664{\delta ^{0.312}}} \right)}}} \right)\frac{{64}}{{Re}}} \right] $ | (19) |
(2) Recr ≤ Re ≤ 22000
| $ {N_{\rm{s, HX}}} = {\pi ^{- 1}} \cdot {\left[{0.023\left[{1 + 14.8\left( {1 + \delta } \right){\delta ^{1/3}}} \right]R{e^{0.8 -0.22{\delta ^{0.1}}}}P{r^{1/3}}} \right]^{ -1}} $ | (20) |
| $ {N_{\rm{s, P}}} = \frac{{{\pi ^3}}}{{32}} \cdot \frac{{R{e^5}}}{{B_0^2}} \cdot \left( {1 + \frac{{28800{\delta ^{0.02}}}}{{Re}}} \right)\frac{{0.3164}}{{R{e^{0.25}}}} $ | (21) |
(3) 20000 ≤ Re ≤ 150000
| $ {N_{\rm{s, HX}}} = {\pi ^{- 1}} \cdot {\left[{0.023\left[{1 + 3.6\left( {1-\delta } \right){\delta ^{0.8}}} \right]R{e^{0.8}}P{r^{1/3}}} \right]^{ -1}} $ | (22) |
| $ {N_{\rm{s, P}}} = \frac{{{\pi ^3}}}{{32}} \cdot \frac{{R{e^5}}}{{B_0^2}} \cdot \left[{1 + 0.0823\left( {1 + \delta } \right){\delta ^{0.58}}R{e^{0.25}}} \right]\frac{{0.3164}}{{R{e^{0.25}}}} $ | (23) |
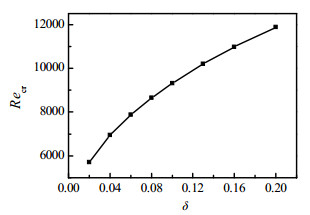
25℃的水在缠绕管内流动,对缠绕管式换热器管程的非平衡热力学特性进行理论研究。缠绕管热流密度为q = 900 W·m-1,内径di= 0.01 m,水的物性如表 1所示。Recr随着δ的变化如图 3所示,Recr随δ呈指数性增大,随着δ的增大,缠绕管的Recr也随之增大。根据式(11)和Re的定义式,可以得到单位长度的压降ΔP (单位:Pa·m-1)的表达式为:
| $ \left| {\Delta P} \right| = \frac{2}{\rho } \cdot \frac{{{{\left( {Re\mu } \right)}^2}}}{{d_i^3}} \cdot f $ | (24) |
|
|
表 1 25℃水的物性[20] Table 1 Physical properties of water at 25℃ |
|
图 3 Schmidt数学模型的Recr随δ的变化趋势 Fig.3 Variation of Recr as a function of δ studied with Schmidt model |
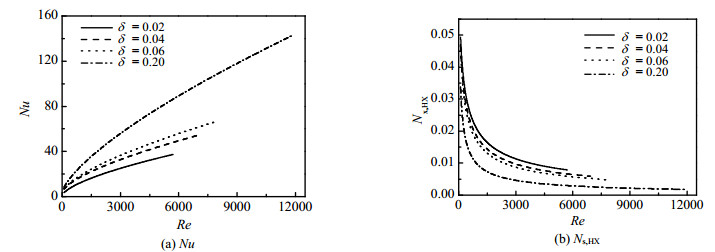
由于Recr随δ呈指数性增大,图 4和图 5中不同δ对应的变化曲线在100 ≤ Re ≤ Recr区域的终点不同。从图 4 (a)可以看出,100 ≤Re ≤ Recr区域内的Nu随着Re的增大而迅速增大,当Recr时达到最大值。这说明随着Re的增大,缠绕管内的强制对流传热性能迅速提高,当δ = 0.20时,Re增大到其对应的Recr = 11887时,Nu增大到130以上。在图 4 (b)中,Ns, HX变化趋势与Nu相反,随着Re的增大,Ns, HX呈现减小的趋势;当Re ≤ 2000时,随着Re的增大,Ns, HX急剧减小;当Re > 2000时,随着Re的增大,Ns, HX减小的趋势明显放缓,直至达到Recr;这说明随着Re的增大,传热不可逆损失越来越小。在图 4 (a)和(b)中,随着δ的增大,Nu呈现增大的趋势,Ns, HX呈现减小的趋势,不同δ对应的Nu和Ns, HX差别很大;当Re = 4000时,δ = 0.2的Nu (67.798)是δ = 0.02的Nu (29.9492)的两倍以上;相反的是,当Re = 4000时,δ = 0.02的Ns, HX (0.009665)是δ = 0.2的Ns, HX (0.003736)的两倍以上;这说明在100 ≤Re ≤Recr区域内,δ对传热及其不可逆损失的影响显著。
|
图 4 100 ≤ Re ≤ Recr区域,缠绕管的Nu和Ns, HX Fig.4 Nu and Ns, HX of the coiled tube at 100 ≤ Re ≤ Recr |
|
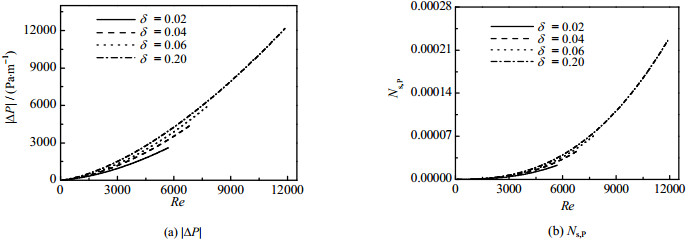
图 5 100 ≤ Re ≤ Recr区域,缠绕管|ΔP|和Ns, P Fig.5 |ΔP| and Ns, P of the coiled tube at 100 ≤ Re ≤ Recr |
图 5 (a)和(b)反映的是缠绕管的阻力性能(压降|ΔP|)以及阻力不可逆损失(Ns, P)。图 5 (a)说明,在100 ≤Re ≤ Recr区域内,随着Re的增大,|ΔP|呈现指数增大的趋势,直至达到Recr;相似的,图 5 (b)中Ns, P随着Re的增大也呈现相同的趋势;当δ = 0.20时,Re增大到其对应的Recr = 11887时,|ΔP|增大到12000 Pa·m-1以上;同时,其相应的Ns, P增大到2.2605×10-4以上;这说明随着Re的增大,缠绕管内阻力及其对应的不可逆损失也越来越大。
从图 4(b)和图 5(b)可知,相较于Ns, HX的变化,Ns, P变化不明显且处于低水平;当Re = 4000时,δ = 0.02对应的Ns, P (9.21483×10-6)与δ = 0.20对应的Ns, P (1.44105×10-5)相差不大且数值很小。综上所述,在100 ≤Re≤ Recr区域内,Ns, HX≫Ns, P,传热不可逆损失Ns, HX占主导地位。
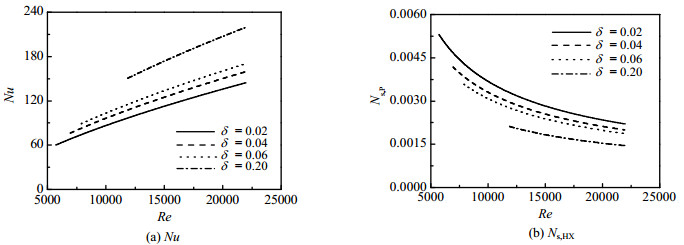
4.2 Recr ≤ Re ≤ 22000区域的非平衡热力学特性由于Recr ≤ Re ≤ 22000区域的起点是Recr,图 6中不同δ对应的变化曲线在范围的起点各异。与图 4反映的趋势类似,从图 5(a)和(b)可知,在Recr ≤ Re ≤ 22000区域内,随着Re的增大,Nu呈现增大的趋势,Ns, HX呈现减小的趋势;随着δ的增大,Nu逐渐增大,Ns, HX逐渐减小。当δ = 0.2时,Re达到Re = 22000时,Nu增大到230以上,Ns, HX减小到0.15以下。当Re = 20000时,δ = 0.2对应的Nu (207.2026)远大于δ = 0.02对应的Nu (135.8538);而δ = 0.02对应的Ns, HX (0.002344)大于δ = 0.2对应的Ns, HX (0.001537)。相较于100 ≤ Re ≤ Recr区域,δ对传热及其不可逆损失在Recr ≤ Re ≤ 22000区域内的影响减小了。
|
图 6 Recr ≤ Re ≤ 22000区域,缠绕管的Nu 和 Ns,HX Fig.6 Nu and Ns,HX of the coiled tube at Recr ≤ Re ≤ 22000 |
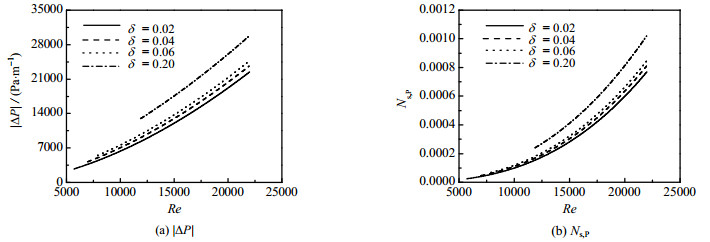
Recr ≤ Re ≤ 22000区域的|ΔP|和Ns, P随着Re的变化趋势分别如图 7 (a)和(b)所示,|ΔP|和Ns, P随着Re的增大,呈现指数性增大的趋势。从图 7 (a)和(b)可知,δ对缠绕管内部阻力及其不可逆损失的影响相对显著;当Re = 22000时,δ = 0.2对应的|ΔP| = 29828.5 Pa·m-1,其相应的Ns, P= 0.00077059。δ = 0.02对应的|ΔP| = 22448 Pa·m-1,其相应的Ns, P = 0.00102695;相较于100 ≤ Re ≤ Recr区域,δ对缠绕管的压降及其不可逆损失在Recr ≤ Re ≤ 22000区域内的影响显著。
|
图 7 Recr ≤ Re ≤ 22000区域,缠绕管的|ΔP|和Ns, P Fig.7 |ΔP| and Ns, P of the coiled tube at Recr ≤ Re ≤ 22000 |
从图 6(b)和图 7(b)可知,当Re = 20000时,δ = 0.2对应的Ns, HX = 0.001537,Ns, P = 0.00081351,Ns, HX > Ns, P;这说明在Recr ≤ Re ≤ 22000区域内,传热不可逆损失依然比重较大,但是Ns, HX和Ns, P的差距在缩小。
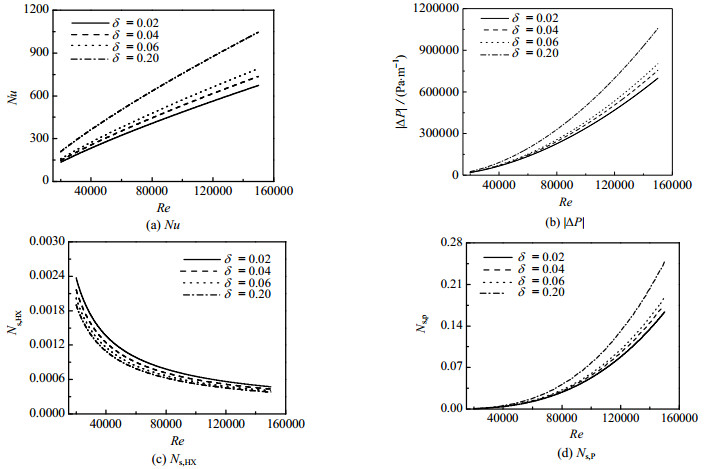
4.3 20000 ≤ Re ≤ 150000区域的非平衡热力学特性Schmidt公式的最后一个区域为20000 ≤ Re ≤ 150000,这与区域Recr ≤ Re ≤ 22000有一定的重叠部分。区域20000 ≤ Re ≤ 150000内的Nu和Ns, HX随着Re的变化趋势如图 8 (a)和(c)所示;与前两个区域类似,随着Re的增大,Nu呈线性增大的趋势,Ns, HX呈减小的趋势。从图 6 (a)和(c)中还可知,随着δ的增大,Nu逐渐增大,Ns, HX逐渐减小;当δ = 0.20,Re = 150000时,Nu增大至Nu = 1046.23,Ns, HX减小到Ns, HX = 0.00037962;当Re = 100000时,δ = 0.20对应的Nu (756.405)远大于δ = 0.02对应的Nu (486.49);而δ = 0.02对应的Ns, HX (0.0006546)大于δ = 0.20对应的Ns, HX (0.0005251)。相较于前两个区域,δ对传热及其不可逆损失在20000 ≤ Re ≤ 150000区域内的影响最小。
|
图 8 20000 ≤ Re ≤ 150000区域,缠绕管的非平衡热力学特性 Fig.8 Thermodynamic characteristics of the coiled tube at 20000 ≤ Re ≤ 150000 |
20000 ≤ Re ≤ 150000区域的|ΔP|和Ns, P随着Re的变化趋势如图 8 (b)和(d)所示,|ΔP|和Ns, P随着Re的增大,呈指数性增大的趋势。从图 8 (b)和(d)可知,δ对缠绕管内部阻力及其不可逆损失的影响相对显著;当Re = 100000时,δ = 0.20的|ΔP| = 497737 Pa·m-1,Ns, P = 0.077665。δ = 0.02的|ΔP| = 338128 Pa·m-1,Ns, P =0.028319;当Re ≤ 60000时,不同δ对应的|ΔP|和Ns, P差别不明显;而当Re > 60000时,不同δ对应的|ΔP|和Ns, P差别明显增大,而且,随着Re的增大,|ΔP|和Ns, P的增幅呈增大的趋势。相较于前两个区域,δ对缠绕管的传热及其不可逆损失在20000 ≤ Re ≤ 150000区域内的影响更为显著。
从图 8 (c)和(d)可知,当Re = 25000时,δ = 0.20的Ns, HX = 0.001591,Ns, P = 0.001501,Ns, P < Ns, HX,Ns, P与Ns, HX相差不大;当Re = 100000时,δ = 0.2对应的Ns, HX = 0.0006546,Ns, P = 0.077665。相较于前两个区域,在20000 ≤ Re ≤ 150000区域内,阻力不可逆损失Ns, P逐渐接近并超过传热不可逆损失Ns, HX,开始占据主导地位。
综上所述,得到了缠绕管内部对流传热的非平衡热力学原理:在不同的流动区域内,Re随Nu呈指数性增大,随Ns, HX呈指数性减小;随着Re的增大,缠绕管内的强制对流传热效果越来越强,强制对流传热引起的传热不可逆损失越来越小。Re随|ΔP|和Ns, P呈指数性增大,随着Re的增大,缠绕管内压降越来越大,其对应的不可逆损失也越来越大。
5 结论以描述缠绕管式换热器管程的Schmidt对流传热关联式为基础,对缠绕管式换热器管程的非平衡热力学理论模型进行了研究,分析了该模型的特性。得到的主要结论如下:
(1) 建立了缠绕管式换热器管程的非平衡热力学理论模型,得到了缠绕管式换热器管程的传热熵产数(Ns, HX)和阻力熵产数(Ns, P)的数学表达式。
(2) 得到了缠绕管内部对流传热的非平衡热力学原理:在不同的流动区域内,Re随Nu呈指数性增大,随Ns, HX呈指数性减小;随着Re的增大,缠绕管内的强制对流传热效果越来越强,强制对流传热引起的传热不可逆损失越来越小。Re随|ΔP|和Ns, P呈指数性增大,随着Re的增大,缠绕管内压降越来越大,其对应的不可逆损失也越来越大。
(3) 得到了传热熵产数(Ns, HX)和阻力熵产数(Ns, P)之间相对关系。在100 ≤ Re ≤ Recr区域内,Ns, HX≫Ns, P,传热不可逆损失Ns, P占主导地位;在Recr ≤ Re ≤ 22000区域内,Ns, HX > Ns, P,传热不可逆损失依然比重较大,Ns, HX和Ns, P的差距在缩小。在20000 ≤ Re ≤ 150000区域内,阻力不可逆损失Ns, P逐渐接近并超过传热不可逆损失Ns, HX,开始占据主导地位。
(4) 主要对缠绕管的非平衡热力学的特性进行了理论研究,不同结构参数、不同物性参数等对传热熵产数(Ns, HX)和阻力熵产数(Ns, P)的影响的数值模拟和实验研究将在接下来的工作进行。
|
|
| [1] | Moawed M. Experimental study of forced convection from helical coiled tubes with different parameters[J]. Energy Conversion and Management, 2011, 52(2): 1150-1156. DOI:10.1016/j.enconman.2010.09.009. |
| [2] | Shokouhmand H, Salimpour M R, Akhavan-Behabadi M A. Experimental investigation of shell and coiled tube heat exchangers using wilson plots[J]. International Communications in Heat and Mass Transfer, 2008, 35(1): 84-92. DOI:10.1016/j.icheatmasstransfer.2007.06.001. |
| [3] | Salimpour M R. Heat transfer coefficients of shell and coiled tube heat exchangers[J]. Experimental Thermal and Fluid Science, 2009, 33(2): 203-207. DOI:10.1016/j.expthermflusci.2008.07.015. |
| [4] | Jamshidi N, Farhadi M, Ganji D D, et al. Experimental analysis of heat transfer enhancement in shell and helical tube heat exchangers[J]. Applied Thermal Engineering, 2013, 51(1-2): 644-652. DOI:10.1016/j.applthermaleng.2012.10.008. |
| [5] | Gilli P V. Heat transfer and pressure drop for cross flow through banks of multistart helical tubes with uniform inclinations and uniform longitudinal pitches[J]. Nuclear Science and Engineering, 1965, 22(3): 298-314. DOI:10.13182/NSE65-A20934. |
| [6] | Schmidt E F. W rmeübergang und druckverlust in rohrschlangen[J]. Chemie Ingenieur Technik, 1967, 39(13): 781-789. DOI:10.1002/(ISSN)1522-2640. |
| [7] | Bejan A. Advanced engineering thermodynamics[M].New York: Wiley, 1997. |
| [8] | Bejan A. Method of entropy generation minimization, or modeling and optimization based on combined heat transfer and thermodynamics[J]. Revue Générale De Thermique, 1996, 35(418-419): 637-646. DOI:10.1016/S0035-3159(96)80059-6. |
| [9] | Bejan A. Second law analysis in heat transfer[J]. Energy, 1980, 5(8-9): 720-732. DOI:10.1016/0360-5442(80)90091-2. |
| [10] | Shokouhmand H, Salimpour M R. Entropy generation analysis of fully developed laminar forced convection in a helical tube with uniform wall temperature[J]. Heat and Mass Transfer, 2007, 44(2): 213-220. DOI:10.1007/s00231-007-0235-x. |
| [11] | Satapathy A K. Thermodynamic optimization of a coiled tube heat exchanger under constant wall heat flux condition[J]. Energy, 2009, 34(9): 1122-1126. DOI:10.1016/j.energy.2009.04.028. |
| [12] | YIN Jie-xi(尹接喜), LI Qing-hai(李清海), SHI De-qiang(施德强), et al. Heat transfer model land experiment for paired-tubes wound-tube heat exchangers(缠绕管换热器并管传热模型及实验)[J]. Journal of Tsinghua University Sci & Tech(清华大学学报(自然科学版), 2000, 40(6): 73-75. DOI:10.3321/j.issn:1000-0054.2000.06.021. |
| [13] | CHEN Yong-dong(陈永东), WU Xiao-hong(吴晓红), ZHOU Bing(周兵). Calculation methods of thermo-physical properties for experimental research on LNG spiral-wound heat exchangers(LNG缠绕管式换热器试验研究中的热物性计算方法)[J]. Natural Gas Industry(天然气工业), 2011, 31(6): 92-97. DOI:10.3787/j.issn.1000-0976.2011.06.020. |
| [14] | CHEN Yong-dong(陈永东), WU Xiao-hong(吴晓红), XIU Wei-hong(修维红), et al. FEA on tube-sheet of a multi-stream spiral wound heat exchanger(多股流缠绕管式换热器管板的有限元分析)[J]. Petro-Chemical Equipment(石油化工设备), 2009, 38(4): 23-27. DOI:10.3969/j.issn.1000-7466.2009.04.006. |
| [15] | LI Jing-yao(李京瑶), GONG Mao-qiong(公茂琼), TANG Qi-xiong(汤奇雄), et al. Design of coiled-wound heat exchanger in small plant of LNG(小型LNG装置缠绕管换热器的设计)[J]. CIESC Journal(化工学报), 2015, 66(S2): 108-115. DOI:10.11949/j.issn.0438-1157.20151061. |
| [16] | XU Cheng-liang(徐成良), DING Guo-zhong(丁国忠). A simple calculation method for helical wound coil tube heat exchangers(绕管式换热器换热面积的一种简捷计算方法)[J]. Low Temperature and Specialty Gases(低温与特气), 2015, 33(1): 1-4. DOI:10.3969/j.issn.1007-7804.2015.01.001. |
| [17] | ZHANG Zhou-wei(张周卫), XUE Jia-xing(薛佳幸), WANG Ya-hong(汪雅红), et al. Research and develop on coil-wound heat exchanger(缠绕管式换热器的研究与开发)[J]. Machinery Design & Manufacture(机械设计与制造), 2015(9): 12-17. DOI:10.3969/j.issn.1001-3997.2015.09.004. |
| [18] | ZHANG Zhou-wei(张周卫), XUE Jia-xing(薛佳幸), WANG Ya-hong(汪雅红). Research on calculation and design method of cryogenic double-stream coil-wound heat exchanger(双股流低温缠绕管式换热器设计计算方法)[J]. Cryogenics(低温工程), 2014(6): 17-23. DOI:10.3969/j.issn.1000-6516.2014.06.004. |
| [19] | Bejan A. Method of entropy generation minimization, or modeling and optimization based on combined heat transfer and thermodynamics[J]. Revue Générale De Thermique, 1996, 35(418-419): 637-646. DOI:10.1016/S0035-3159(96)80059-6. |
| [20] | SHEN Wei-dao(沈维道), TONG Jun-geng(童钧耕). Engineering thermodynamics(工程热力学)[M].4th ed.Beijing(北京): Higher Education Press(高等教育出版社), 2007. |
| [21] | Welty J R, Wicks C E. Fundamentals of momentum, heat, and mass transfer[M].New York: Wiley, 1976. |




