2. 大连理工大学 数学科学学院, 辽宁 大连 116024
2. School of Mathematical Science, Dalian University of Technology, Dalian 116024, China
蒸汽动力系统通过将一次能源(燃料等)转化为二次能源(电、蒸汽等),为过程工业提供所需要的工艺蒸汽、热能和动力[1-2]。在蒸汽动力系统的实际优化调度中不可避免包含不确定因素。不确定因素会使系统现有操作偏离最优状态,造成过程的不合理,甚至带来安全隐患,所以在蒸汽动力系统优化调度中进行不确定优化研究具有重要的理论和实际意义[3-4]。
对于蒸汽动力系统的不确定优化调度研究,传统的处理方法是将不确定问题转变为确定性多周期问题进行求解,即划分成多个周期,在每个周期内取不确定变量的期望值进行优化[5-10]。但实际上在每个周期内外部工艺或生产过程的随机波动还会引起不确定变量的随机变化,传统确定性方法不能真实地反映不确定变量对优化目标和约束条件的影响,可能导致设计和操作偏离最优状态[3-4, 11]。目前解决不确定优化问题的主要数学规划方法有随机规划[12-14]、模糊规划[15-17]、鲁棒优化[18-20]和区间规划[21-22]等。廖组维等[23]针对不精确的过程数据,提出在不确定情况下蒸汽动力系统调度问题的模糊模型;Sun等[24]考虑设备故障和汽电需求不确定变化建立了带补偿的两阶段随机规划模型;盖丽梅等[3, 11]将不确定变量划分为基于时间表达和基于发生概率表达两类,提出了带补偿的两阶段随机规划模型。
然而,实际系统中存在多种不确定性,且这些不确定性通常不是单独存在的。单一的不确定优化方法在解决实际问题中都有各自的适用条件和优缺点,不能应对复杂的不确定系统。因此,不确定优化方法耦合解决复杂的不确定问题已经成为众多领域的研究热点[25-31]。目前不确定方法耦合鲜有应用于公用工程,特别是蒸汽动力系统的设计和优化。本文考虑蒸汽动力系统优化模型中同时存在的多类型不确定变量,并将不确定变量划分为2个等级。第1等级是基于时间表达的不确定变量,进行多周期离散化处理。第2等级出现在各个周期,包括基于发生概率表达和基于集合表达的不确定变量,耦合机会约束规划和鲁棒优化,建立机会约束鲁棒优化模型。通过实际案例将本文模型与传统模型进行分析对比。
2 考虑多类型不确定变量的蒸汽动力系统运行优化模型不确定变量的表达可以分成2个等级。第1等级是基于时间变化表达的不确定变量,如季节气候、加工方案等因素引起的汽电需求周期性变化;由于季节变化引起能源市场需求的变化从而导致燃料价格、电价和蒸汽价格的波动。对基于时间变化表达的变量,转化为多周期问题进行处理,即将全周期(一年)划分为
以
| $\begin{array}{*{20}{c}} {{{\mathop {\min }\limits_\boldsymbol{X} }_{{{\overline {{\rm{pri}}} }_{{\rm{e,}}T}}}}{{\mathop {\max }\limits_{{{\overline {{\rm{pri}}} }_{{\rm{i}},T}}} }_{{{\overline {{\rm{pri}}} }_{{\rm{i}},T}}}}\sum\limits_T {\sum\limits_{\rm{n}} {\left( {{\rm{C}}{{\rm{M}}_{\rm{n}}} \times {Y_{{\rm{n}},T}} \times \tau + \sum\limits_{\rm{i}} {{F_{{\rm{n}},{\rm{i}},T}}} \times {{\overline {{\rm{pri}}} }_{{\rm{i}},T}} \times {Y_{{\rm{n}},T}} \times \tau + {\rm{CS}}{{\rm{U}}_{\rm{n}}} \times {Z_{{\rm{n}},T}} + {\rm{CS}}{{\rm{D}}_{\rm{n}}} \times {\rm{Z}}{{\rm{S}}_{{\rm{n}},T}}} \right)} } + }\\ {\sum\limits_T {\left( {{\rm{pu}}{{\rm{r}}_{{\rm{e}},T}} \times {{\overline {{\rm{pr}}} }_{{\rm{e}},T}} + \sum\limits_{\rm{r}} {{{{\mathop{\rm pur}\nolimits} }_{{\rm{r}},T}}} \times {{\overline {{\rm{pr}}} }_{{\rm{r}},T}} \times \tau } \right)} + \sum\limits_T {{\rm{EV}}} \times {L_T} \times \tau } \end{array} $ | (1) |
式中:
| $\begin{array}{l} \min \gamma \\ \begin{array}{*{20}{l}} {{\rm{ s}}{\rm{.t}}{\rm{. }}\sum\limits_T {\sum\limits_{\rm{n}} {\left( {{\rm{C}}{{\rm{M}}_{\rm{n}}} \times {Y_{{\rm{n}},T}} \times \tau + \sum\limits_{\rm{i}} {{F_{{\rm{n}},{\rm{i}},T}}} \times {{\overline {{\rm{pri}}} }_{{\rm{i}},T}} \times {Y_{{\rm{n}},T}} \times \tau + {\rm{CS}}{{\rm{U}}_{\rm{n}}} \times {Z_{{\rm{n}},T}} + {\rm{CS}}{{\rm{D}}_{\rm{n}}} \times {\rm{Z}}{{\rm{S}}_{{\rm{n}},T}}} \right)} } + }\\ {\sum\limits_T {\left( {{{{\mathop{\rm pur}\nolimits} }_{{\rm{e}},T}} \times {{\overline {{\rm{pri}}} }_{{\rm{e}},T}} + \sum\limits_{\rm{r}} {{{{\mathop{\rm pur}\nolimits} }_{{\rm{r}},T}}} \times {{\overline {{\rm{pri}}} }_{{\rm{r}},T}} \times \tau } \right)} + \sum\limits_T {{\rm{EV}}} \times {L_T} \times \tau \le \gamma } \end{array} \end{array}$ | (2) |
证明问题(2)等价于问题(1)。
定理 如果问题(1)存在最优解,则问题(2)也存在最优解;如果
证明:为表述方便,定义
| $\begin{array}{*{20}{c}} {f\left( {\boldsymbol{X},{{\overline {{\rm{pr}}} }_{\rm{e}}},{{\overline {{\rm{pr}}} }_{\rm{i}}},{{\overline {{\rm{pr}}} }_{\rm{r}}}} \right) = \sum\limits_T {\sum\limits_{\rm{n}} {\left( {{\rm{C}}{{\rm{M}}_{\rm{n}}} \times {Y_{{\rm{n}},T}} \times \tau + \sum\limits_{\rm{i}} {{F_{{\rm{n}},{\rm{i}},T}}} \times {{\overline {{\rm{pr}}} }_{{\rm{i}},T}} \times {Y_{{\rm{n}},T}} \times \tau + {\rm{CS}}{{\rm{U}}_{\rm{n}}} \times {Z_{{\rm{n}},T}} + {\rm{CS}}{{\rm{D}}_{\rm{n}}} \times {\rm{Z}}{{\rm{S}}_{{\rm{n}},T}}} \right)} } + }\\ {\sum\limits_T {\left( {{{{\mathop{\rm pur}\nolimits} }_{{\rm{e}},T}} \times {{\overline {{\rm{pr}}} }_{{\rm{e}},T}} + \sum\limits_{\rm{r}} {{{{\mathop{\rm pur}\nolimits} }_{{\rm{r}},T}}} \times {{\overline {{\rm{pr}}} }_{{\rm{r}},T}} \times \tau } \right)} + \sum\limits_T {{\rm{EV}}} \times {L_T} \times \tau } \end{array} $ | (3) |
对
| $\mathop {\max }\limits_{{{\overline {{\rm{pri}}} }_{\rm{e}}},{{\overline {{\rm{pri}}} }_{\rm{i}}},{{\overline {{\rm{pri}}} }_{\rm{r}}}} f\left( {\boldsymbol{X},{{\overline {{\rm{pri}}} }_{\rm{e}}},{{\overline {{\rm{pri}}} }_{\rm{i}}},{{\overline {{\rm{pri}}} }_{\rm{r}}}} \right) = f\left( {\boldsymbol{X},{{\overline {{\rm{pri}}} }_{\rm{e}}},{{\overline {{\rm{pri}}} }_{\rm{i}}},{{\overline {{\rm{pri}}} }_{\rm{r}}}} \right) = l(\boldsymbol{X})$ | (4) |
则
| $f\left(\boldsymbol{X}, \overline{\mathrm{pri}}_{\mathrm{e}}, \overline{\mathrm{pri}}_{\mathrm{i}}, \overline{\mathrm{pri}}_{\mathrm{r}}\right) \leqslant f\left(\boldsymbol{X}, \overline{\mathrm{pri}}^{*}, \overline{\mathrm{pri}}^{*}, \overline{\mathrm{pri}}_{\mathrm{r}}^{*}\right)=l(\boldsymbol{X})$ | (5) |
由式(4)和(5)可得
| $\mathop {\min }\limits_\mathit{\boldsymbol{X}} \mathop {\max }\limits_{{{\overline {{\rm{pri}}} }_{\rm{e}}},{{\overline {{\rm{pri}}} }_{\rm{i}}},{{\overline {{\rm{pri}}} }_{\rm{r}}}} f\left( {\mathit{\boldsymbol{X}},{{\overline {{\rm{pri}}} }_{\rm{e}}},{{\overline {{\rm{pri}}} }_{\rm{i}}},{{\overline {{\rm{pri}}} }_{\rm{r}}}} \right) \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {\mathop {\min }\limits_\mathit{\boldsymbol{X}} l(X)}\\ {{\rm{ s}}{\rm{.t}}{\rm{. }}f\left( {\mathit{\boldsymbol{X}},{{\overline {{\rm{pri}}} }_{\rm{e}}},{{\overline {{\rm{pri}}} }_{\rm{i}}},{{\overline {{\rm{pri}}} }_{\rm{r}}}} \right) \le l(\mathit{\boldsymbol{X}})} \end{array}} \right.$ | (6) |
引入变量
| $\left\{ {\begin{array}{*{20}{c}} {\mathop {\min }\limits_\mathit{\boldsymbol{X}} l(X)}\\ {{\rm{ s}}{\rm{.t}}{\rm{. }}f\left( {\mathit{\boldsymbol{X}},{{\overline {{\rm{pri}}} }_{\rm{e}}},{{\overline {{\rm{pri}}} }_{\rm{i}}},{{\overline {{\rm{pri}}} }_{\rm{r}}}} \right) \le l(\mathit{\boldsymbol{X}})} \end{array} \Leftrightarrow } \right.\left\{ {\begin{array}{*{20}{c}} {\min \gamma }\\ {{\rm{ s}}{\rm{.t}}{\rm{. }}f\left( {\mathit{\boldsymbol{X}},{{\overline {{\rm{pri}}} }_{\rm{e}}},{{\overline {{\rm{pri}}} }_{\rm{i}}},{{\overline {{\rm{pri}}} }_{\rm{r}}}} \right) \le \gamma } \end{array}} \right.$ | (7) |
由式(6)和(7)可得
| $\mathop {\min }\limits_\mathit{\boldsymbol{X}} \mathop {\max }\limits_{{{\overline {{\rm{pri}}} }_{\rm{e}}},{{\overline {{\rm{pri}}} }_{\rm{i}}},{{\overline {{\rm{pri}}} }_{\rm{r}}}} f\left( {\mathit{\boldsymbol{X}},{{\overline {{\rm{pri}}} }_{\rm{e}}},{{\overline {{\rm{pri}}} }_{\rm{i}}},{{\overline {{\rm{pri}}} }_{\rm{r}}}} \right) \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {\min \gamma }\\ {{\rm{ s}}{\rm{.t}}{\rm{. }}f\left( {\mathit{\boldsymbol{X}},{{\overline {{\rm{pri}}} }_{\rm{e}}},{{\overline {{\rm{pri}}} }_{\rm{i}}},{{\overline {{\rm{pri}}} }_{\rm{r}}}} \right) \le \gamma } \end{array}} \right.$ | (8) |
综上,问题(2)等价于问题(1)。定理得证。
2.2 锅炉的能量守恒约束在蒸汽动力系统中,锅炉以燃料油或燃料气等为燃料,将水加热成高温高压蒸汽,用以满足生产加工过程中换热、做功或发电的需要。根据能量守恒定律,锅炉的所有供给能量之和等于流出能量之和,如式(9)所示。
| $S_{\mathrm{n}, \text { boi }} \times\left(h_{\mathrm{n}, \mathrm{boi}, \mathrm{out}}-h_{\mathrm{n}, \mathrm{boi}, \mathrm{in}}\right)=\sum\limits_{\mathrm{i}} F_{\mathrm{n}, \mathrm{i}} \times q_{\mathrm{i}} \times \eta_{\mathrm{n}, \mathrm{boi}}$ | (9) |
式中:
汽轮机将蕴含在高温高压蒸汽中的热能转化为机械能或电能。在实际生产中,改变汽轮机的抽汽量是调节蒸汽管网中不同等级蒸汽平衡的重要手段之一。Shang等[32]改进了背压式汽轮机的数学模型,提高了模型的精度,如式(10)所示。
| ${P_{\mathrm{n}, \text { tur}}} = \frac{6}{{5B}}({h_{\mathrm{n}, \text { tur},\text { out}}} - {h_{\mathrm{n}, \text { tur},\text { in}}} - \frac{A}{{S_{\mathrm{n}, \text { tur},\text { in}}^{\max }}})({S_{\mathrm{n}, \text { tur},\text { in}}} - \frac{1}{6}S_{\mathrm{n}, \text { tur},\text { in}}^{\max })$ | (10) |
式中:Pn, tur为汽轮机功率,kW;
设备n在周期T的工作负荷应处于正常范围,如式(11)所示。
| $Y_{\mathrm{n}, T} \times S_{\mathrm{n}}^{\min } \leqslant S_{n, T} \leqslant Y_{\mathrm{n}, T} \times S_{\mathrm{n}}^{\max }$ | (11) |
式中:
在炼厂中,设备的平稳运行对于安全生产至关重要,设备频繁启停一方面会减少设备使用寿命,增加维修成本,另一方面还会影响正常的工作质量,降低炼油企业生产效益,所以需要对设备运行状态的变化进行约束。
| $\begin{array}{c} Z_{\mathrm{n}, T} \geqslant Y_{\mathrm{n}, T}-Y_{n, T-1} \end{array}$ | (12) |
| $\mathrm{ZS}_{\mathrm{n}, T} \geqslant Y_{\mathrm{n}, T}-Y_{\mathrm{n}, T+1}$ | (13) |
蒸汽动力系统在向过程工业提供工艺蒸汽、动力及电力等的同时也消耗大量的化石燃料,而这些燃料中均含有一定量S、C、N元素,燃烧之后产生一定量对环境有害的大气污染物
| ${{L_T}\left( {{\rm{S}}{{\rm{O}}_2}} \right) = \sum\limits_{\rm{i}} {\sum\limits_{\rm{n}} 2 } \times {F_{{\rm{n}},{\rm{i}},T}} \times {w_{{\rm{S}},{\rm{i}}}} \times \left( {1 - {\eta _{{\rm{des}}}}} \right) \times {Y_{{\rm{n}},T}}}$ | (14) |
| ${{L_T}\left( {{\rm{C}}{{\rm{O}}_2}} \right) = \sum\limits_{\rm{i}} {\sum\limits_{\rm{n}} 3 } .667 \times {F_{{\rm{n}},{\rm{i}},T}} \times {w_{{\rm{C}},{\rm{i}}}} \times {\lambda _{\rm{i}}}\left( {{\rm{C}}{{\rm{O}}_2}} \right) \times {Y_{{\rm{n}},T}}}$ | (15) |
| ${{L_T}\left( {{\rm{N}}{{\rm{O}}_2}} \right) = \sum\limits_{\rm{i}} {\sum\limits_{\rm{n}} 1 } .63 \times {F_{{\rm{n}},{\rm{i}},T}} \times \left( {{w_{{\rm{N}},{\rm{i}}}} \times {\lambda _{\rm{i}}}\left( {{\rm{N}}{{\rm{O}}_2}} \right) + 0.000938} \right) \times {Y_{{\rm{n}},T}}}$ | (16) |
式中:
供需约束主要是满足蒸汽动力系统对蒸汽、动力和电力的需求。考虑汽电需求等不确定变量且在每一周期基于发生概率表达,应用机会约束规划策略。机会约束规划是随机规划的重要分支,主要针对约束条件中含有随机变量,且必须在观测到随机变量的实现之前作出决策的情况。考虑到所做决策在不利情况发生时可能不满足约束条件,而采取一整原则:即允许所做决策在一定程度上不满足约束条件,但该决策应使约束条件成立的概率不小于某一置信水平[12, 33]。得到机会约束式(17)、(18)如下所示:
蒸汽需求约束:
| $Pr\{ \operatorname{pur}_{\mathrm{r}, T} + \sum\limits_{\rm{n}} {{S_{\rm{n, boi, T}}}} + \sum\limits_{\rm{n}} {({S_{\rm{n, tur, out, }T}} - {S_{\rm{n, tur, in, T}}})} + \sum\limits_{\rm{n}} {({S_{\rm{n, red, out, }T}} - {S_{\rm{n, red, in, }T}}) \geqslant {{\overline D }_{\mathrm{r}, T}}\} \geqslant \alpha } $ | (17) |
式中:
电力需求约束:
| ${\Pr _{}}\{ \sum\limits_{\rm{n}} {{P_{{\rm{n, tur, }}T}}} + \operatorname{pur}_{\mathrm{e}, T} \geqslant {{\bar D}_{{\rm{e}},T}}\} \geqslant \beta $ | (18) |
式中:Pn, tur, T为汽轮机在周期T内功率,kW;
处理机会约束规划的方法是把机会约束转化为各自的确定等价形式[34]。机会约束式(17)、(18)的确定等价形式分别为
| $\operatorname{pur}_{\mathrm{r}, T} + \sum\limits_{\rm{n}} {{S_{\rm{n, boi, T}}}} + \sum\limits_{\rm{n}} {({S_{\rm{n, tur, out, }T}} - {S_{\rm{n, tur, in, T}}})} + \sum\limits_{\rm{n}} {({S_{\rm{n, red, out, }T}} - {S_{\rm{n, red, in, }T}})} \geqslant {K_\alpha }$ | (19) |
| $\sum\limits_{\rm{n}} {{P_{n, T}}} + \operatorname{pur}_{\mathrm{e}, T} \geqslant {K_\beta }$ | (20) |
式中:
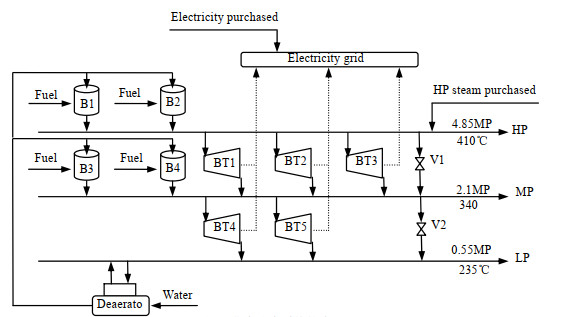
实例为某炼油厂工程项目的蒸汽动力,工艺流程如图 1所示。有3种等级蒸汽,高压蒸汽(HP)、中压蒸汽(MP)和低压蒸汽(LP)。B1-B4为锅炉,参数见表 1。BT1-BT5为汽轮机,参数见表 2。V1-V2为减温减压器,容量为60 t·h-1。系统燃料为天然气,其C元素的质量分数为78%,燃烧热值为50 244 kJ·kg-1,C的氧化率为99%。
|
图 1 蒸汽动力系统的流程图 Fig.1 Flowsheet of a steam power system |
|
|
表 1 锅炉参数 Table 1 Parameters of the boiler |
|
|
表 2 汽轮机参数 Table 2 Parameters of the turbine |
由于市场环境的变化,汽电需求、蒸汽价格、电价以及燃料价格都属于不确定变量。传统模型是将不确定问题转变为确定性多周期问题进行求解,即划分成多个周期,在每个周期内取不确定变量的期望值进行优化。本文对基于时间变化表达的汽电需求、高压蒸汽价格、电价以及燃料价格等变量按多周期处理,即将全周期(一年)划分为6个周期,每个周期按100 h计算。在每个周期,对基于发生概率表达的汽电需求变量应用机会约束规划策略。置信水平由决策者提供适当的安全裕度,具体取值取决于企业愿意承担的风险系数。本文选择置信水平α=0.9,β=0.9。根据实际经验以及对历史数据的概率统计,基于发生概率表达的汽电需求变量服从正态分布,其概率函数为
|
|
表 3 各周期汽电需求标称值 Table 3 Normal demands of steam and electricity in each period |
|
|
表 4 价格数据 Table 4 Price data |
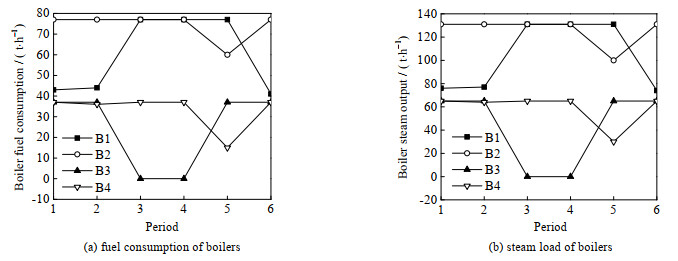
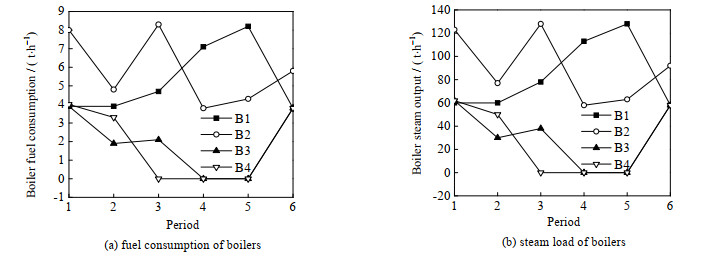
基于LINGO 11.0求解器,确定在不确定环境下的最优运行策略。决策变量包括各周期锅炉、汽轮机和减温减压器负荷、锅炉燃料消耗、外购高压蒸汽量、外购电量和设备的二元变量。本文模型包含162个连续变量,78个离散变量,415个线性约束和6个非线性约束。传统模型包含162个线性变量,48个离散变量,378个线性约束和1个非线性约束。如图 2和3所示分别为本文模型和传统模型计算得到的锅炉的最优操作方案。从图中可以看出,在全周期内本文模型的优化方案中只有锅炉B3有一次启停;传统模型的优化方案中B3,B4都存在启停情况;另外,相比于传统模型,本文模型的锅炉优化运行负荷较稳定,变化幅度不大,且运行负荷较高使得设备运行效率也更高。综上所述,本文模型的锅炉优化方案一方面能更有效地避免由于设备频繁启停或者负荷波动过大而引起的设备故障问题,另一方面能提高锅炉运行效率,经济性越好。
|
图 2 本文模型的锅炉最优操作方案 Fig.2 The boiler optimal operation schemes obtained using the proposed model |
|
图 3 传统模型的锅炉最优操作方案 Fig.3 The boiler optimal operation schemes obtained using the traditional model |
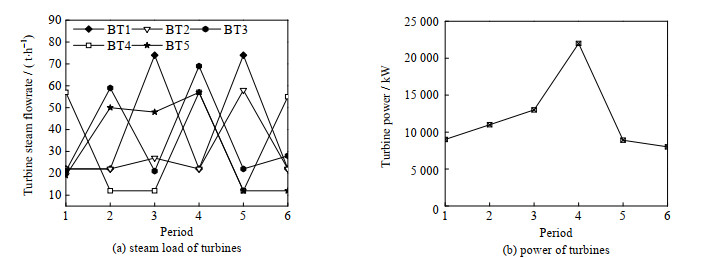
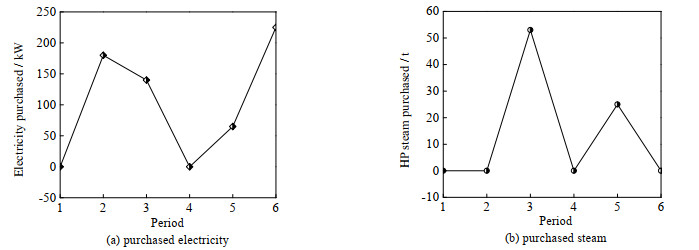
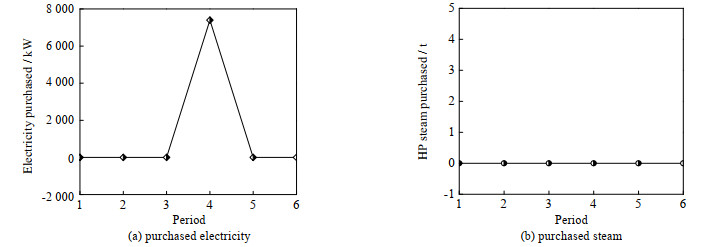
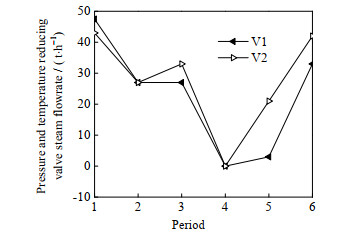
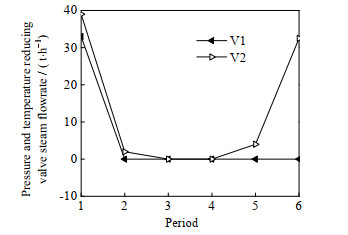
如图 4和5所示为本文模型和传统模型计算得到的汽轮机的最优操作方案。从图中可以看出,2种模型的优化方案中汽轮机都不存在启停情况,不过运行负荷都存在较大波动;在第4周期本文模型的汽轮机以较大功率运行,所以在全周期内本文模型的优化方案中自产电量明显高于传统模型的自产电量。从而导致本文模型的外购电量相比如传统模型大幅度减少,见图 6和7。另外,本文模型的优化方案中需要外购少量的高压蒸汽。如图 8和9所示为2种模型的减温减压器最优操作方案。从图中可以看出,2种操作方案都存在少量的能源浪费。
|
图 4 本文模型的汽轮机最优操作方案 Fig.4 The turbine optimal operation schemes obtained using the proposed model |
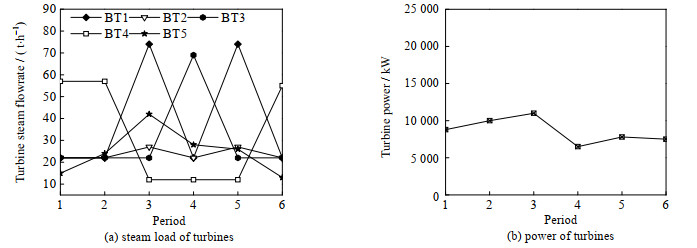
|
图 5 传统模型的汽轮机最优操作方案 Fig.5 The turbine optimal operation schemes obtained using the traditional model |
|
图 6 本文模型的最优外购方案 Fig.6 The optimal outsourcing schemes obtained using the proposed model |
|
图 7 传统模型的最优外购方案 Fig.7 The optimal outsourcing schemes obtained using the traditional model |
|
图 8 本文模型的减温减压器最优操作方案 Fig.8 The optimal operation schemes for the pressure and temperature reducing valve obtained using the proposed model |
|
图 9 传统模型的减温减压器最优操作方案 Fig.9 The optimal operation schemes for the pressure and temperature reducing valve obtained using the traditional model |
蒸汽动力系统在各个周期内提供的电力、蒸汽量在满足用户需求的条件下,增加系统自身负荷,减少外购是降低成本的最优方案。在设备的额定工况内,设备的运行负荷越大,设备的运行效率就越高,经济性越好。与传统模型相比,本文模型的优化方案中大量的自产电导致设备燃料消耗增加,燃料花费增加了6.68%,环境成本增加了22.5%,不过外购电力以及设备启停次数的减少使得本文模型的优化方案总花费降低了1.7%,这证明了本文模型的经济性能,见表 5。
|
|
表 5 费用对比 Table 5 Cost comparison |
(1) 本文针对蒸汽动力系统中的不确定性进行分析分类,不同类型不确定性应用不同的策略建立其对目标函数和约束的影响。建立蒸汽动力系统运行优化模型。案例研究表明:与传统模型相比,本文模型的优化方案不仅使总花费降低了1.7%,而且能获得在复杂不确定性下具有可接受风险的鲁棒性决策, 保证系统应对不同类型的不确定变量而安全稳定运行。
(2) 本文模型的优化方案相对保守,且设备故障等不确定性问题还没有考虑。下一步将继续研究系统中存在的不确定性,针对不同类型不确定性开发更好的处理策略。
| [1] |
徐乐, 陈颖, 罗向龙. 考虑减排措施的蒸汽动力系统结构优选[J]. 热科学与技术, 2011, 10(4): 371-376. XU L, CHEN Y, LUO X L. Structure optimization of steam power system with emission reduction technology concerns[J]. Journal of Thermal Science and Technology, 2011, 10(4): 371-376. DOI:10.3969/j.issn.1671-8097.2011.04.018 |
| [2] |
李帅, 姜晓滨, 贺高红, 等. 蒸汽动力系统柔性设计和多目标优化研究进展[J]. 化工进展, 2017, 36(6): 1989-1996. LI S, JIANG X B, HE G H, et al. Research progress for flexible design and multi-objective optimization of steam power network[J]. Chemical Industry and Engineering Progress, 2017, 36(6): 1989-1996. |
| [3] |
盖丽梅, 孙力, 刘畅, 等. 基于带补偿随机规划的蒸汽动力系统优化设计[J]. 化工学报, 2014, 65(11): 4509-4516. GAI L M, SUN L, LIU C, et al. Steam power system optimization design based on stochastic programming with recourse[J]. CIESC Jorunal, 2014, 65(11): 4509-4516. DOI:10.3969/j.issn.0438-1157.2014.11.042 |
| [4] |
盖丽梅. 基于随机规划的不确定蒸汽动力系统优化设计[D]. 大连: 大连理工大学, 2015. GAI L M. Optimal design of uncertain steam power system based on stochastic programming[D]. Dalian: Dalian University of Technology, 2015. |
| [5] |
IYER R R, GROSSMANN I E. Synthesis and operational planning of utility systems for multiperiod operation[J]. Computers & Chemical Engineering, 1998, 22(7-8): 979-993. |
| [6] |
YI H S, HAN C, YEO Y K. Optimal multiperiod planning of utility systems considering discrete/continuous variance in internal energy demand based on decomposition method[J]. Journal of Chemical Engineering of Japan, 2000, 33(3): 456-467. DOI:10.1252/jcej.33.456 |
| [7] |
AGUILAR O, PERRY S J, KIM J K. Design and optimization of flexible utility systems subject to variable conditions(q): Methodology and applications[J]. Chemical Engineering Research and Design, 2007, 85(8): 1149-1168. DOI:10.1205/cherd06063 |
| [8] |
罗向龙, 陈颖, 华贲. 参数不确定性条件下蒸汽动力系统的运行优化[J]. 石油学报(石油加工), 2009, 25(2): 233-240. LUO X L, CHEN Y, HUA B. Operational planning optimization of utility system under parameters uncertainty[J]. Acta Petrolei Sinica (Petroleum Processing Section), 2009, 25(2): 233-240. DOI:10.3969/j.issn.1001-8719.2009.02.017 |
| [9] |
李晖, 孙力, 贺高红. 考虑不确定汽电需求的蒸汽动力系统优化设计[J]. 化工学报, 2013, 64(1): 325-332. LI H, SUN L, HE G H. Design and optimization of steam power system with uncertain steam and power demands[J]. CIESC Journal, 2013, 64(1): 325-332. |
| [10] |
徐东, 史彬, 鄢烈祥. 基于不同碳减排目标的蒸汽动力系统优化[J]. 计算机与应用化学, 2017, 34(2): 114-118. XU D, SHI B, YAN L X. Optimization for steam power system based on different carbon reduction targets[J]. Computers and Applied Chemistry, 2017, 34(2): 114-118. |
| [11] |
SUN L, GAI L M, SMITH R. Site utility system optimization with operation adjustment under uncertainty[J]. Applied Energy, 2017, 186(3): 450-456. |
| [12] |
SHAPIRO A, DENTCHEVA D, RUSZYNSKI A. Lectures on stochastic programming: Modeling and theory[M]. Philadelphia: Society for Industrial Mathematics, 2009.
|
| [13] |
张冰剑, 陈清林, 华贲. 油轮到达时间不确定条件下的原油调度优化[J]. 高校化学工程学报, 2009, 23(3): 500-509. ZHANG B J, CHEN Q L, HUA B. Optimizing crude oil scheduling under the uncertainty of tank ship arrival time[J]. Journal of Chemical Engineering of Chinese Universities, 2009, 23(3): 500-509. DOI:10.3321/j.issn:1003-9015.2009.03.025 |
| [14] |
ALIPOUR M, ZARE K, SEYEDI H. A multi follower Bi-level stochastic programming approach for energy management of combined heat and power micro-grids[J]. Energy, 2018, 149(15): 135-146. |
| [15] |
钱宇, 肖宏亮. 模糊系统的模型化和优化[J]. 高校化学工程学报, 1996, 10(3): 309-315. QIAN Y, XIAO H L. Modelling and optimization for fuzzy systems[J]. Journal of Chemical Engineering of Chinese Universities, 1996, 10(3): 309-315. |
| [16] |
LENCE B J, MOOSAVIAN N, DALIRI H. Fuzzy programming approach for multiobjective optimization of water distribution systems[J]. Journal of Water Resources Planning and Management, 2017, 143(7): 04017020. DOI:10.1061/(ASCE)WR.1943-5452.0000769 |
| [17] |
REN C, LI Z, ZHANG H. Integrated multi-objective stochastic fuzzy programming and AHP method for agricultural water and land optimization allocation under multiple uncertainties[J]. Journal of Cleaner Production, 2019, 210(10): 12-24. |
| [18] |
BEN-TAL A, NEMIROVSKI A. Robust optimization-methodology and applications[J]. Mathematical Programming, 2002, 92(3): 453-480. DOI:10.1007/s101070100286 |
| [19] |
VAN BAREL A, VANDEWALLE S. Robust optimization with a multilevel monte carlo method[J]. Siam/asa Journal on Uncertainty Quantification, 2019, 7(1): 174-202. DOI:10.1137/17M1155892 |
| [20] |
KAPTEYN M G, WILLCOX K E, PHILPOTT A B. Distributionally robust optimization for engineering design under uncertainty[J]. International Journal for Numerical Methods in Engineering, 2019, 120(3): 835-859. |
| [21] |
LIU Z, HUANG Y. Sustainable distributed biodiesel manufacturing under uncertainty: An interval-parameter-programming-based approach[J]. Chemical Engineering Science, 2013, 93(8): 429-444. |
| [22] |
SINGH A. Managing the uncertainty problems of municipal solid waste disposal[J]. Journal of Environmental Management, 2019, 240(15): 259-265. |
| [23] |
廖祖维, 宣吉, 荣冈, 等. 基于模糊规划的石化企业蒸汽动力系统调度优化[J]. 浙江大学学报(工学版), 2011, 45(4): 621-626. LIAO Z W, XUAN J, RONG G, et al. Fuzzy programming based scheduling of steam power system in petrochemical complex[J]. Journal of Zhejiang University (Engineering Science), 2011, 45(4): 621-626. DOI:10.3785/j.issn.1008-973X.2011.04.006 |
| [24] |
SUN L, LIU C. Reliable and flexible steam and power system design[J]. Applied Thermal Engineering, 2015, 79: 184-191. DOI:10.1016/j.applthermaleng.2014.11.076 |
| [25] |
WU H H, KÜÜKYAVUZ S. A two-stage stochastic programming approach for influence maximization in social networks[J]. Computational Optimization and Applications, 2017, 69(1): 1-33. |
| [26] |
HE Y, HE Z, LEE D H, et al. Robust fuzzy programming method for MRO problems considering location effect, dispersion effect and model uncertainty[J]. Computers & Industrial Engineering, 2017, 105: 76-83. |
| [27] |
李进. 低碳环境下闭环供应链网络设计多目标鲁棒模糊优化问题[J]. 控制与决策, 2018, 33(2): 293-300. LI J. Multi-objective robust fuzzy optimization problem for closed-loop supply chain network design under low-carbon environment[J]. Control and Decision, 2018, 33(2): 293-300. |
| [28] |
SIMIC V. Interval-parameter conditional value-at-risk two-stage stochastic programming model for management of end of life vehicles[J]. Environmental Modeling and Assessment, 2019, 24(5): 547-567. DOI:10.1007/s10666-018-9648-9 |
| [29] |
AKBARI-DIBAVAR A, ZARE K, NOJAVAN S. A hybrid stochastic-robust optimization approach for energy storage arbitrage in day-ahead and real-time markets[J]. Sustainable Cities and Society, 2019, 49: 101600. DOI:10.1016/j.scs.2019.101600 |
| [30] |
陈红光, 王中君, 王琼雅, 等. 基于区间两阶段-部分信息模型的城市水资源优化配置[J]. 资源科学, 2019, 41(8): 1416-1426. CHEN H G, WANG Z J, WANG Q Y, et al. An interval-parameter two-stage partial information programming model for optimal urban water resource planning[J]. Resources Science, 2019, 41(8): 1416-1426. |
| [31] |
叶雁犁, 刘洋, 陈贤邦. 考虑源荷双侧不确定的孤岛型微网能量管理优化模型[J]. 水电能源科学, 2020, 38(1): 191-195. YE Y L, LIU Y, CHEN X B. Energy management optimization model of island microgrid with uncertain generation and load[J]. Water Resources and Power, 2020, 38(1): 191-195. |
| [32] |
SHANG Z, KOKOSSIS A. A transhipment model for the optimisation of steam levels of total site utility system for multiperiod operation[J]. Computers & Chemical Engineering, 2004, 28(9): 1673-1688. |
| [33] |
CHARNES A, COOPER W W. Chance-constrained programming[J]. Management Science, 1959, 6(1): 73-79. DOI:10.1287/mnsc.6.1.73 |
| [34] |
LIU B D. Theory and practice of uncertain programming [M]. Berlin: Springer-Verlag Berlin and Heidelberg GmbH & Co. KG, 2009.
|




