2. 可再生能源建筑利用技术省部共建教育部重点实验室,山东 济南 250101;
3. 山东省可再生能源建筑应用技术重点实验室,山东 济南 250101
2. Key Laboratory of Renewable Energy Utilization Technologies in Building, Ministry of Education, Jinan 250101, China;
3. Shandong Key Laboratory of Renewable Energy Application Technology, Jinan 250101, China
扭曲管因具有较好的强化传热性能得到关注,它的发展弥补了传统管壳式换热器的许多不足。目前,扭曲管换热器已广泛应用于化工、石油、造纸、电力、钢铁等诸多行业。由于扭曲管的多点自支撑结构,与传统圆管换热器相比,扭曲管换热器具有传热系数高、压降小、无振动、少结垢、易清洗、去折流板等一系列特点[1]。最先是在1984年,由瑞典的Alards公司设计并且制造研究的。随后,美国的Brown公司对其进行了进一步的优化。一般认为流体在管内周期性的螺旋流动可以使流体冲刷壁面,减薄边界层。从20世纪80年代起,俄罗斯的一些学者就开展了一系列的研究,主要侧重于研究流体在螺旋扁管管束中各管相互支撑形成的通道内流动特征、传热传质性能及流动阻力等[2~5]。螺旋椭圆扭曲管换热器的传热机理比较复杂,为了进一步改进螺旋椭圆扭曲管换热器的结构和提高它的传热性能,国内外不少学者已经对螺旋椭圆扭曲管单向扭曲的换热流动情况进行了研究并取得了不少成果。例如我国的梁龙虎[6]对螺旋椭圆管与光管的换热和阻力情况作了实验对比研究;张杏祥等[7]对螺旋椭圆管的传热与流阻特性进行了模拟分析;刘敏珊等[8]模拟了螺旋椭圆管与螺旋扁管在雷诺数小于1000时的换热特性;高学农等[9]研究了高扭曲比的螺旋椭圆管的传热与流阻性能。
上述这些强化技术虽然已取得了相当广泛的应用,但是普遍存在传热强化的同时,流动阻力(或功耗)增加更多的问题。它们基本上是现有技术的改进,缺乏一些基于新概念创新性的传热强化技术[10]。过增元院士[10]从流场和温度场相互配合的角度重新审视对流换热物理机制,在此基础上提出了换热强化的场协同原则。不仅能统一地认识现有各种对流换热和传热强化现象的物理本质,更重要的是它能指导发展新的传热强化技术,其思路与现有强化技术有很大不同,而且在传热强化的同时, 阻力(或功耗)低得多, 更有利于节能和工程应用。通过调节流场,减小速度矢量U和温度梯度矢量∇T之间的夹角来实现强化传热;减小速度矢量U和压降梯度矢量-∇P之间的夹角来实现流动减阻。
本文基于场协同原理采用CFD的流固共轭传热技术对扭曲椭圆管进行了数值模拟,模拟以水为流体的管道内速度场、压力场及温度场,并且依据场协同原理对其强化传热效果进行分析。
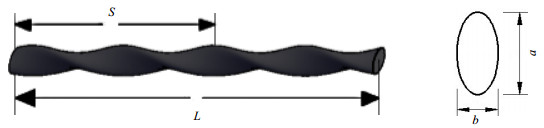
2 几何模型及控制方程 2.1 几何模型在数值计算中, 扭曲椭圆管扭曲2π即为一个扭程S。选取管长均为L = 300 mm,截面面积均为6.28×10-4 m2,扭曲角度均为4 π,扭曲比S/d均为11.9,截面为椭圆且长轴为a、短轴为b的扭曲管进行数值模拟,几何模型如图 1所示。
|
图 1 扭曲管几何模型 Fig.1 Geometric model of a twisted tube |
在数值模拟中,扭曲椭圆管的管壁材料设置为铝,因该模拟主要着重于管内流体的传热及流阻,故暂不考虑壁厚影响,设壁厚为零。
为了研究扭曲椭圆管截面短长轴比对其传热及流阻性能的影响,模拟计算选取总长度相等,扭曲比相同的扭曲管,模拟计算的扭曲管如表 1所示。
| 表 1 不同短长轴比的扭曲管 Table 1 Twisted tubes with different short and long axis ratios |
所有型号的扭曲管送水速度和水的初始温度均分别为0.01 m·s-1和293.15 K,管件壁面给定壁温353.15 K。
2.2 控制方程以管件的整个流动区域中的流体为研究对象,建立数学模型。管件内流体流动的控制方程[11]为:
连续性方程
| $ \frac{\partial \left( \rho u \right)}{\partial \mathit{\boldsymbol{x}}}+\frac{\partial \left( \rho v \right)}{\partial \mathit{\boldsymbol{y}}}+\frac{\partial \left( \rho w \right)}{\partial \mathit{\boldsymbol{z}}}=0 $ | (1) |
动量方程
| $ \begin{align} &u\frac{\partial u}{\partial \mathit{\boldsymbol{x}}}+v\frac{\partial u}{\partial \mathit{\boldsymbol{y}}}+w\frac{\partial u}{\partial \mathit{\boldsymbol{z}}}=-\frac{1}{{{\rho }_{0}}}\frac{\partial p}{\partial \mathit{\boldsymbol{x}}}+\eta (\frac{{{\partial }^{2}}u}{\partial {{\mathit{\boldsymbol{x}}}^{2}}}+\frac{{{\partial }^{2}}u}{\partial {{\mathit{\boldsymbol{y}}}^{2}}}+\frac{{{\partial }^{2}}u}{\partial {{\mathit{\boldsymbol{z}}}^{2}}}) \\ &u\frac{\partial v}{\partial \mathit{\boldsymbol{x}}}+v\frac{\partial v}{\partial \mathit{\boldsymbol{y}}}+w\frac{\partial v}{\partial \mathit{\boldsymbol{z}}}=-\frac{1}{{{\rho }_{0}}}\frac{\partial p}{\partial \mathit{\boldsymbol{y}}}+\eta (\frac{{{\partial }^{2}}v}{\partial {{\mathit{\boldsymbol{x}}}^{2}}}+\frac{{{\partial }^{2}}v}{\partial {{\mathit{\boldsymbol{y}}}^{2}}}+\frac{{{\partial }^{2}}v}{\partial {{\mathit{\boldsymbol{z}}}^{2}}}) \\ &u\frac{\partial w}{\partial \mathit{\boldsymbol{x}}}+v\frac{\partial w}{\partial \mathit{\boldsymbol{y}}}+w\frac{\partial w}{\partial \mathit{\boldsymbol{z}}}=-\frac{1}{{{\rho }_{0}}}\frac{\partial p}{\partial \mathit{\boldsymbol{z}}}+\eta (\frac{{{\partial }^{2}}w}{\partial {{\mathit{\boldsymbol{x}}}^{2}}}+\frac{{{\partial }^{2}}w}{\partial {{\mathit{\boldsymbol{y}}}^{2}}}+\frac{{{\partial }^{2}}w}{\partial {{\mathit{\boldsymbol{z}}}^{2}}}) \end{align} $ | (2) |
能量方程
| $ u\frac{\partial T}{\partial \mathit{\boldsymbol{x}}}+v\frac{\partial T}{\partial \mathit{\boldsymbol{y}}}+w\frac{\partial T}{\partial \mathit{\boldsymbol{z}}}=a(\frac{{{\partial }^{2}}T}{\partial {{\mathit{\boldsymbol{x}}}^{2}}}+\frac{{{\partial }^{2}}T}{\partial {{\mathit{\boldsymbol{y}}}^{2}}}+\frac{{{\partial }^{2}}T}{\partial {{\mathit{\boldsymbol{z}}}^{2}}}) $ | (3) |
式中:u为流体的x方向速度分量;m·s-1;v为流体的y方向速度分量,m·s-1;w为流体的z方向速度分量,m·s-1;p为流体的压力,Pa;T为流体的温度,K;η为流体的黏性系数,Pa·s-1;a为流体的热扩散系数,m2·s-1;ρ为流体的密度,kg·m-3;ρ0为流体的参考工作密度,kg·m-3;x为x方向的矢量,m;y为y方向的矢量,m;z为z方向的矢量,m。
3 网格检验及求解方法 3.1 网格独立性检验为确保数值模拟计算结果的准确性和可靠性,对b/a= 1的扭曲管模型划分3种不同数量的网格数进行网格无关性验证。不同网格数量下,管道各截面平均温度的变化情况如图 2所示,网格数量为1.49×105及1.85×105时的管道各截面平均温度与网格数量为2.25×105时的结果相差范围分别为-5.4×10-4~ 6.9×10-4和1.9×10-4~ 4.3×10-4,考虑到计算机性能和计算时间,选用网格数量为1.85 105最为合理。

|
图 2 不同网格数下管道不同截面的平均温度 Fig.2 Average temperatures in different cross sections of tubes with different meshes |
采用CFD建立物理模型并划分网格,计算过程中采用有限容积法离散方程,同时求解流体的连续性方程,动量方程和能量方程。选取层流模型,采用二阶迎风差分格式进行离散,控制方程的求解利用SIMPLE算法。进口边界条件给定水的进口平均流速、进口温度;出口边界条件设定相对压力为零。当能量方程中收敛残差小于10-6时,整个计算过程被认为收敛。并且计算做了如下基本假设:(l)水的物性参数为常数;(2)流体在壁面上无滑移;(3)流体的流动是定常的;(4)不考虑在重力方向上浮升力的影响。
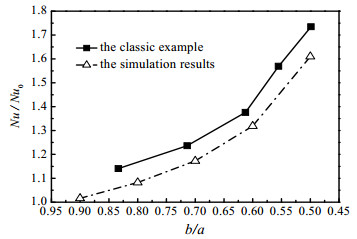
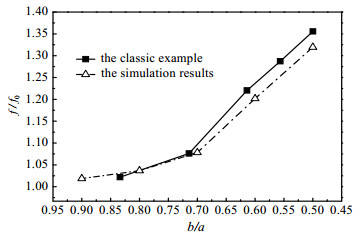
4 计算结果及比较 4.1 数值模拟验证以权威国际期刊国际传热传质文献[12]中的在Re = 500时Nu的增长率Nu/Nu0以及f的增长率f/f0数值模拟结果作为本文参考算例,采用本文中几何模型,设定Re = 500,将计算结果与算例进行对比,对比结果如图 3与图 4,且Nu/Nu0误差最大为5.16%,f/f0误差最大为2.63%,故认为模拟结果是有效的。
|
图 3 Nu/Nu0随b/a变化的对比图 Fig.3 Comparison of Nu/Nu0-b/a profiles between simulation and classic example results |
|
图 4 f/f0随b/a变化的对比图 Fig.4 Comparison of f/f0-b/a profiles between simulation and classic example results |
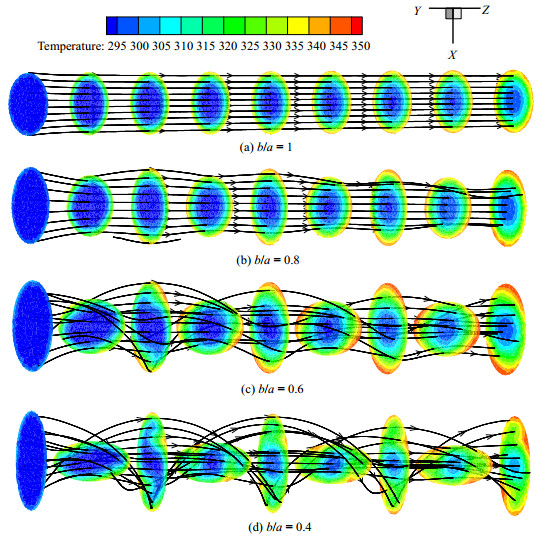
因几何模型之间区别仅为横截面短长轴比不同,且流体流动趋势一致,故取其中短长轴比为1、0.8、0.6、0.4的四个几何模型为例进行解释。且每个截面均为管道每扭转90°所取的切面。
从图 5中可以看出,每条管道内的流体温度均越来越高,且经数值模拟计算,b/a = 1的扭曲管内流体的平均温度为311.07 K,b/a = 0.8的扭曲管内流体的平均温度为311.57 K,b/a = 0.6的扭曲管内流体的平均温度为313.58 K,b/a = 0.4的扭曲管内流体的平均温度为315.97 K,故随着管道越扁,流体温度升高越快。图 5(a)的流体流动没有二次流的出现,而扭曲椭圆管内有明显的二次流出现,二次流随着管道越扁即短长轴比越小越明显。图 5(b)中的二次流为上下扰动,图 5(c)及图 5(d)中二次流的主要形态为以换热管轴线为中心的螺旋流。扭曲椭圆管内的流动有着很强的旋转特性,从图 5中可看出由于管道的扭曲导致流体流动方向的扭曲变形,靠近管壁处可以看出,流体有冲击热边界层的趋势,通过模拟计算分析可以看出:扭曲椭圆管结构使得管内流体产生旋转流动,迫使流体改变了流动方向,在扭转同时使流体冲击了管道壁面,从而使热边界层厚度减薄,并且管道越扁,这个趋势越明显即流体速度矢量线与截面上温度梯度的夹角越小,从而流体速度与温度梯度的协同程度就越好,这有利于强化换热。
|
图 5 扭曲管的温度场截面图及速度流线图 Fig.5 Temperature sectional diagram and velocity streamline diagram of twisted tubes |
层流的能量协同方程[13]:
| $ Nu=RePr\int_{0}^{{\delta }/{h}\;}{\left( \mathit{\boldsymbol{U}}\cdot \nabla \mathit{\boldsymbol{T}} \right)\rm{d}\mathit{Y}} $ | (4) |
式中:Nu,Re,Pr分别为努塞尔数、雷诺数和普朗特数;∇T为温度梯度。
无因次速度与无因次温度梯度的点积可表达为:
| $ \mathit{\boldsymbol{U}}\cdot \nabla \mathit{\boldsymbol{T}}=\left| \mathit{\boldsymbol{U}} \right|\left| \nabla \mathit{\boldsymbol{T}} \right|\rm{cos}\theta $ | (5) |
若矢量U与矢量T之间的夹角越小,则点积U·∇T越大,努塞尔数Nu越大,流体与壁面间的对流换热也就越强。从而可推出协同角表达式为:
| $ \theta =\rm{arccos}\frac{\mathit{\boldsymbol{U}}\cdot \nabla \mathit{\boldsymbol{T}}}{\left| \mathit{\boldsymbol{U}} \right|\left| \nabla \mathit{\boldsymbol{T}} \right|} $ | (6) |
基于场协同原理可得出速度与温度梯度的协同程度即协同角。协同角图及等值线图如图 6所示:
|
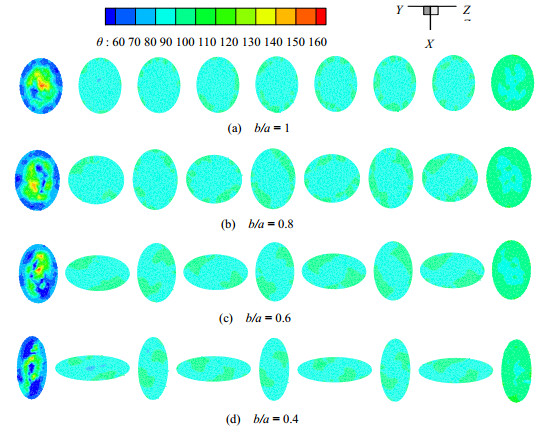
图 6 扭曲管截面的速度与温度梯度协同角的等值线图 Fig.6 Synergy angle contour of velocity-temperature gradient for twisted tube sections |
根据图 6协同角云图可知,管道入口端处流体速度与温度梯度的协同程度不稳定,在入口截面上可以看出协同角大至约170°,说明此处速度与温度梯度的协同很差,不仅不会强化换热更会弱化传热;而同一截面上协同角还有部分位置小至约20°,说明此处速度与温度梯度的协同很好,有利于强化传热。因协同角分布不均,无法对管道进行整体换热效果对比,故对截面取平均协同角进行分析,判断管道强化换热的优劣:
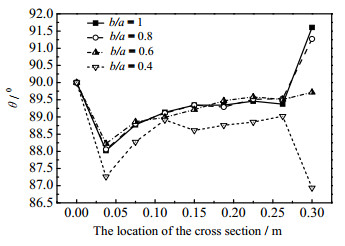
由图 7可知,进口处各管道的平均协同角均为90°,对换热效果不起作用,在管道0.075 m处之前以及在0.175 ~ 0.2625 m处可以看出θb/a=0.4 < θb/a=1 ≤ θb/a=0.8 ≤ θb/a=0.6 < 90°,所有管道的协同角均小于90°,故知在此管段中所有管道都起到强化换热作用,又由于对比可知此管段中b/a = 0.4的管道强化换热效果最好,b/a = 0.6管道换热效果最差。在0.075 ~ 0.175 m处可以看出θb/a=0.4 < θb/a=0.6 < θb/a=0.8 ≤ θb/a=1 < 90°,所有管道的协同角均小于90°,故知在此管段中所有管道都起到强化换热作用,又由于对比可知此管段中b/a = 0.4的管道强化换热效果最好,b/a = 1管道换热效果最差。在出口端处可以明显看出θb/a=0.4 < θb/a=0.6 < θb/a=0.8 < θb/a=1,故知此管段b/a = 0.4的管道强化换热效果优于b/a = 0.6的管道,b/a = 0.8的管道及b/a = 1的管道弱化传热,且b/a = 1的管道弱化传热最显著。从图整体可以看出b/a = 0.4的管道强化传热效果最好,其他管道每一管段强化换热效果优劣对比结果不同,故取每条管道的速度与温度梯度的平均协同角进行比较,验证整条管道的传热性能的优劣。
|
图 7 管道不同截面平均协同角 Fig.7 Average synergy angles in different tube cross sections |
根据场协同原理中的层流能量协同方程,引入管道速度与温度梯度的平均协同角θ的计算,计算结果如表 2。
| 表 2 管道速度与温度梯度的平均协同角 Table 2 verage synergy angles of velocity-temperature gradient for different tubes |
由表 2可以看出,管道截面平均协同角随截面压扁程度的增大,即截面的短长轴b/a的比值减小而逐渐减小。根据公式(6)可知θ值越小,则点积U·∇T越大,相应努塞尔数Nu越大,流体与壁面间的对流换热也就越强。故由表 2可知扭曲椭圆管截面短长轴之比越小,强化换热效果也就越好。
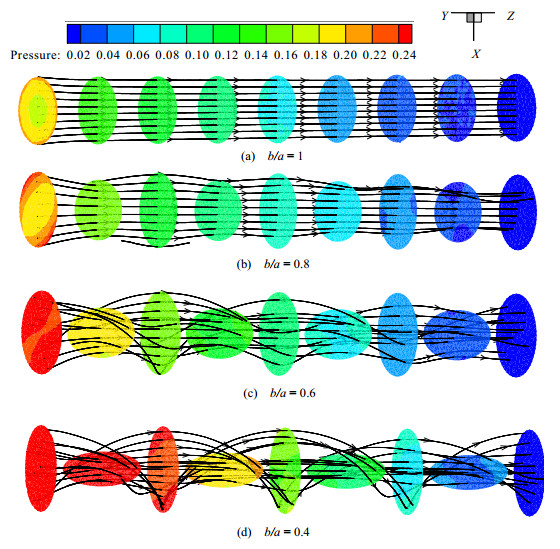
4.3 速度场与压力场的协同分析从图 8中可以看出,每条管道内的流体压力均越来越低,且经数值模拟计算,b/a = 1的扭曲管内流体的压降为0.209 Pa,b/a = 0.8的扭曲管内流体的压降为0.225 Pa,b/a = 0.6的扭曲管内流体的压降为0.279 Pa,b/a = 0.4的扭曲管内流体的压降为0.408 Pa。故随着管道越扁,即随着短长轴比减小,流体进出口压降越大。图 8(a)的流体流动没有二次流的出现,而扭曲椭圆管内有明显的二次流出现,二次流随着管道越扁即短长轴比越小越明显。图 8(b)中的二次流为上下扰动,图 8(c)及图 8(d)中二次流的主要形态为以换热管轴线为中心的螺旋流。扭曲椭圆管内的流动有着很强的旋转特性,从图 8中可看出由于管道的扭曲导致流体流动方向的扭曲变形,并且管道越扁,流体的旋转特性越强,从而迫使流体冲击管道壁面,加大了流体速度与压降梯度的夹角,造成速度与压降梯度的协同程度变差,增大了阻力损失。
|
图 8 扭曲管的压力场截面图及速度流线图 Fig.8 Pressure sectional diagram and velocity streamline diagram of twisted tubes |
速度U与压力梯度∇P之间的协同关系表达为[13]:
| $ \mathit{\boldsymbol{U}}\cdot \left( -\nabla \mathit{\boldsymbol{P}} \right)=\left| \mathit{\boldsymbol{U}} \right|\left| -\nabla P \right|\rm{cos}\ \mathit{j} $ | (7) |
从而可推出协同角表达式为:
| $ j=\rm{arccos}\frac{\mathit{\boldsymbol{U}}\cdot \left( -\nabla \mathit{\boldsymbol{P}} \right)}{\left| \mathit{\boldsymbol{U}} \right|\left| -\nabla \mathit{\boldsymbol{P}} \right|} $ | (8) |
若点积U·(-∇P)一定,j角越小,流体的功耗|U||-∇p|越小。由此可见, 减小协同角j意味着降低流体消耗的泵功, 提高设备的节能效果。
基于场协同原理及协同角公式可得出速度与压力梯度的协同程度即协同角。协同角云图如图 9所示:
|
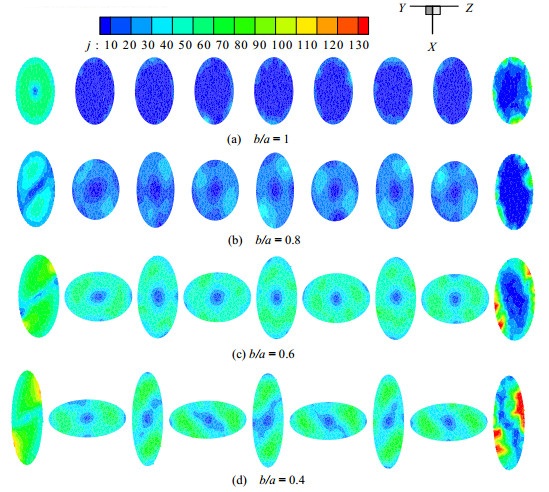
图 9 扭曲管截面的速度与压降梯度的协同角等值线图 Fig.9 Synergy angle contour of velocity-pressure drop gradient for twisted tube sections |
根据图 9协同角云图并且经数值模拟计算可知,b/a = 1的扭曲管协同角大至约70°,小至约10°,整体较趋向减阻;b/a = 0.8的扭曲管协同角大至约70°,小至约10°,整体较趋向减阻;b/a = 0.6的扭曲管协同角大至约130°(此处则为增阻部位),小至约10°;b/a = 0.4的扭曲管协同角大至约130° (此处则为增阻部位),小至约10°。因截面协同角分布不均,无法对管道进行整体流阻效果对比,故对截面取平均协同角进行分析,判断管道流阻的优劣:
由图 10可知,进、出口处各管道的平均协同角均为90°,对流阻问题没有意义,在管道0.15 m之前以及0.225 m至出口处可以看出jb/a=1 < jb/a=0.8 < jb/a=0.6 ≤ jb/a=0.4,可知随着管道截面压扁程度的加大,速度与压降梯度的协同程度越差,即流动阻力也随着增大。在管道0.15 m直至0.225 m处可以看出jb/a=1 < jb/a=0.8 < jb/a=0.4 ≤ jb/a=0.6,可知此处管段b/a = 0.6的管道速度与压降梯度的协同程度最差,流动阻力最大。每一管段速度与压降梯度的对比结果不同,故取每条管道的速度与压降梯度的平均协同角进行比较,验证管道的阻力损失的大小。

|
图 10 管道不同截面平均协同角 Fig.10 Average synergy angles in different tube cross sections |
根据场协同原理,为了更好比较各管道内流体流动的流动阻力损失,通过定量分析流体速度场和压力场的协同程度来解决。根据场协同原理,引入平均协同角j的计算,计算结果如下表 3。
| 表 3 各管道速度与压降梯度的平均协同角 Table 3 The average synergy angle of velocity and pressure drop gradient for different tubes |
由表 3可以看出,管道截面平均协同角随短长轴比的减小逐渐增大。根据公式(8)可知j值越大,流体的功耗|U||-∇P|越大。由此可知扭曲椭圆管的短长轴比越小,管道内的流动阻力损失也就越大。
4.4 流动传热综合分析将扭曲椭圆管传热性能、阻力性能分别用传热系数h、达西阻力系数j来表示。
扭曲扁管的h定义为:
| $ h=\frac{m{{c}_{\rm{p}}}\Delta T}{{A}'\left( {{T}_{\rm{w}}}-{{T}_{\rm{f}}} \right)} $ | (9) |
扭曲扁管的f定义为[14]:
| $ f=\frac{2\Delta Pd}{L\rho {{U}^{2}}} $ | (10) |
式中,m为质量流量,kg·s-1;cp为流体比热容,J·kg-1·k-1;ΔT为管段进出口温差,K;A'为管段表面积,m2;Tw为壁面温度,K;Tf为参考温度,取管内流体混合平均温度,K;d为通道的当量直径,m;ΔP为管段进出口压降,Pa;L为管段长度,m;ρ为流体密度,kg·m-3;U为流道截面上的平均速度,m·s-1。
根据以上各式,计算结果如表 4。
| 表 4 各型号数据 Table 4 Data of various models |
根据以上模拟结果以及计算结果,通过流体速度场和压力场协同程度以及速度场和温度场协同程度的定量分析,可以得出以下各管道之间的比较图。
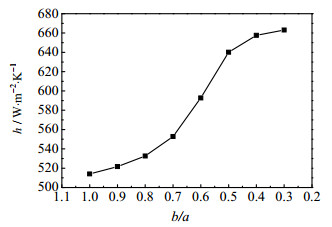
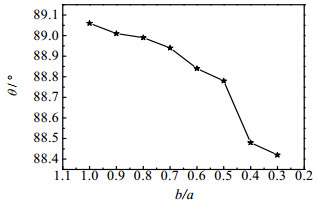
根据图 11可知,随着管道越扁即短长轴比b/a越小,传热系数h越大,在b/a= 0.8~0.5,传热系数h随着b/a的减小急剧增大。由图 12可知,随着管道越扁即短长轴比b/a越小,速度与温度梯度的平均协同角越小,说明流体速度与温度梯度的协同程度随着b/a的减小而越好,根据速度场与温度场的协同分析,认为整个流动区域内,流动速度与温度梯度的协同程度越好即协同角越小,换热效果就越好。故可知随着管道短长轴比的减小,管道的强化换热效果越好。
|
图 11 各型号管道传热系数比较图 Fig.11 Heat transfer coefficients of various tubes |
|
图 12 各型号管道速度与温度梯度的平均协同角比较图 Fig.12 Average synergy angles of velocity-temperature gradient for various tubes |
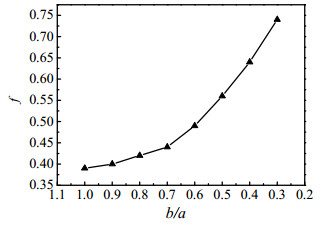
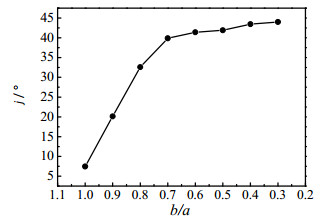
根据图 13可知,随着管道越扁即短长轴比b/a越小,达西阻力系数f越大,随着b/a的减小,f增大越迅速。由图 14可知,随着管道越扁即短长轴比b/a越小,速度与压降梯度的平均协同角越大,说明流体速度与压降梯度的协同程度随着b/a的减小而越差,根据速度场与压力场的协同分析,认为整个流动区域内,流动速度与压降梯度的协同程度越差即协同角越大,阻力损失就越大。故可知随着管道短长轴比的减小,管道的阻力损失逐渐增大。
|
图 13 各型号管道的达西阻力系数的比较图 Fig.13 Darcy drag coefficients for various tubes |
|
图 14 各型号管道速度与压降梯度的平均协同角比较图 Fig.14 Average synergy angles of velocity-pressure drop gradient for various tubes |
通过利用CFD软件对管道内的流体流动进行数值模拟,发现流体的速度场和温度场协同程度直接影响管道的换热能力,以及压力场和速度场协同程度直接影响管道的流动阻力损失。基于场协同原理进一步获得管道内流动流体的速度与温度梯度的平角协同角,以及速度与压力梯度的平均协同角,并以此平均协同角和经过计算所得管道流体的传热系数h和达西阻力系数f判断扭曲管的换热与流阻特性。计算结果表明:(1)扭曲椭圆管相对于扭曲圆管几何参数的变化引起了换热管内的二次流,二次流的出现改变了扭曲管横截面温度场以及速度场分布,同时也改变了扭曲管传热系数h和达西阻力系数f的分布,根据场协同原理,二次流的出现降低了管内速度场与温度梯度场之间的夹角,从而实现了换热管的强化传热;加大了速度场与压降梯度场之间的夹角,增大了流动损失。(2)通过数值模拟结果显示,扭曲管的短长轴比b/a越小,扭曲管的强化传热性能就越好,但是同时流阻也会增大。(3)流体速度场与温度场协同程度越好,强化传热效果越好;流体速度场和压力场协同程度越差,则局部阻力损失越大。(4)本文研究表明,利用CFD软件对管道内流体流动进行基于场协同原理的数值模拟,可有效实现管道内流体流动减阻性能的优化,为工程上的开发和设计强化换热的管道提供理论依据。
| [1] | JU Zai-tang(鞠在堂). Spiral flat tube heat exchanger(螺旋扁管换热器)[J]. Chemical Equipment Technology(化工装备术) , 2003, 24(5): 19-22. |
| [2] | Vilemas Y V, Dzyubenko B V, Sakalauskas A B. Investigation of flow structure in heat exchanger with helically twisted tubes[J]. Power Engineering , 1980, 18(4): 116-123. |
| [3] | Dzyubenko B V, Ashmantas L V A, Segal M D, et al. Unsteady-state mixing of the heat-transport medium in a heat exchanger with twisted tubes[J]. Power Engineering , 1983, 21(3): 116-124. |
| [4] | Dzyubenko B V, Ashmantas L A, Segal M D. Unsteady heat and mass transfer in a heat exchanger with twisted tubes[J]. Power Engineering , 1985, 23(4): 102-110. |
| [5] | Dzyubenko B V, Dreitser G A. Heat transfer and fluid friction in bundles of twisted tubes[J]. Journal of Engineering Physics , 1986, 50(6): 611-618. DOI:10.1007/BF00871525. |
| [6] | LIANG Long-hu(梁龙虎). The performance and industrial application research in the flat spiral tube heat exchanger(螺旋扁管换热器的性能及工业应用研究)[J]. Petroleum Refinery Engineering(炼油设计) , 2001, 8(31): 28-33. |
| [7] | ZHANG Xing-xiang(张杏祥), SANG Zhi-fu(桑芝富). The simulation and analysis of heat transfer and resistance performance of spirally twisted flat tubes(螺旋扭扁管强化传热与阻力性能的模拟分析)[J]. Chemical Engineering & Machinery(化工机械) , 2006, 33(1): 24-28. |
| [8] | LIU Min-shan(刘敏珊), GONG Ben-xi(宫本希), DONG Qi-wu(董其伍). The study on heat transfer performance of spiral flat tube(螺旋扁管的换热性能研究)[J]. China Petroleum Machinery(石油机械) , 2008, 2(36): 22-25. |
| [9] | GAO Xue-nong(高学农), ZOU Hua-chun(邹华春), WANG Duan-yang(王端阳), et al. Heat transfer and flow resistance in a twisted flat tube with high twist ratio(高扭曲比螺旋扁管的管内传热及流阻性能)[J]. Journal of South China University of Technology (Natural Science Edition)(华南理工大学学报(自然版)) , 2008, 11(36): 17-21. |
| [10] | GUO Zeng-yuan(过增元). Field synergy principle and application in heat exchangers(换热器中的场协同原则及其应用)[J]. Journal of Mechanical Engineering(机械工程学报) , 2003, 39(12): 1-9. DOI:10.3321/j.issn:0577-6686.2003.12.001. |
| [11] | TAO Wen-quan(陶文铨). Numerical heat transfer(数值传热学)[M].Xi'an(西安): Xi'an Jiaotong University Press(西安交通大学出版社), 1998. |
| [12] | Cheng J, Qian Z, Wang Q. Analysis of heat transfer and flow resistance of twisted oval tube in low Reynolds number flow[J]. International Journal of Heat & Mass Transfer , 2017, 109: 761-777. |
| [13] | LIU Wei(刘伟), LIU Zhi-chun(刘志春), MA Lei(马雷). Application of multi field synergy principle to performance evaluation of convection enhanced heat transfer in tubes(多场协同原理在管内对流强化传热性能评价中的应用)[J]. Chinese Science Bulletin(科学通报) , 2012(10): 867-874. |
| [14] | Webb R L, Eckert E R G. Application of rough surfaces to heat exchanger design[J]. International Journal of Heat & Mass Transfer , 1972, 15(9): 1647-1658. |
| [15] | ZHU Dong-sheng(朱冬生), SHI Zhong-jing(石仲璟), QIAN Tai-lei(钱泰磊), et al. Numerical simulation and field synergy analysis of a twisted elliptical tube heat exchanger(扭曲椭圆管换热器的数值模拟及场协同分析)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报) , 2015, 29(1): 64-71. |
| [16] | ZHANG Yang-le(张洋乐). Numerical simulation of flow field in different torque twist tube(不同扭距扭曲管管内流场的数值模拟)[J]. Petro-Chemical Equipment Technology(石油化工设备技术) , 2016, 37(3): 13-16. |
| [17] | Ebrahimi A, Roohi E. Numerical study of flow patterns and heat transfer in mini twisted oval tubes[J]. International Journal of Modern Physics C , 2015, 26(12): 295-312. |
| [18] | HAN Yong(韩勇), WANG Ding-biao(王定标), ZHANG Can-can(张灿灿), et al. Numerical study on heat transfer performance of elliptical inner ribbed twisted tube(椭圆内肋扭曲管换热性能数值研究)[J]. Journal of Engineering Thermophysics(工程热物理学报) , 2015, 36(12): 2707-2710. |
| [19] | GUAN Ping(管屏), AN Fang-tao(安方涛), LU Mei(卢玫). Numerical simulation of heat transfer performance of helical twisted flat tube(螺旋扭曲扁管管外传热性能数值模拟)[J]. Light Industry Machinery(轻工机械) , 2016, 34(6): 15-20. |
| [20] | WANG Ding-biao(王定标), WANG Hong-bin(王宏斌), LIANG Zhen-xiang(梁珍祥). Numerical study on heat transfer and flow resistance of twisted trefoil tubes(扭曲三叶管传热与流阻性能的数值研究)[J]. CIESC Journal(化工学报) , 2012, 63(7): 2064-2069. |




