2. 中国检验检疫科学研究院,北京 100176
2. Chinese Academy of Inspection and Quarantine, Beijing 100176, China
毛细管液相色谱是一种高效的色谱分离技术,具有固定相用量少,流动相消耗少,样品消耗少,环境污染少等优点[1]。毛细管液相色谱的核心部件是毛细管柱,其管径通常为毫米级与微米级,由于表面张力与壁面粘附力占主导地位,毛细管中流体特性与大尺寸管道中流体具有非常大的区别[2]。
弹状流是毛细管中常见两相流流型之一,弹状流的特点是:某一相均匀子弹形状的液滴或气泡被另一相分隔,液滴或气泡与管壁之间有薄薄的液膜[3]。气泡的形状、气泡速度、液弹长度及液膜厚度是非常重要的流体力学参数[4]。毛细管中弹状流的压降、传质与液弹长度有关[5],且液膜厚度也会影响传热速率与传质速率,因为液膜的存在增加了界面面积,因而在传质过程中起决定性作用[6]。然而不能像其他参数一样(如表观速度和流体的物理性质)预先确定液膜厚度、液弹的长度及液弹的速度等重要的流体力学参数。对于微通道中两相流的流体力学已有很多实验研究[7~11]。目前虽有一些气液弹状流的实验与模拟研究[5, 12~17]和液液弹状流的实验研究[18~21],大部分研究液液弹状流的压降[18]、内部循环[19]与传质[21]问题,但对于微通道中液液弹状流的流体力学的分析还不是很清楚。且大多数文献研究的是气液弹状流,由于分散相的黏度,液液弹状流的界面剪切力显著,因此,液液弹状流的液膜厚度、液弹速度与液弹长度可能不同于气液弹状流[8]。所以有必要系统地研究液液弹状流的流体力学特性。本文以T型毛细管为模型,使用计算流体力学的方法研究毛细管中液液弹状流的流体力学特性。研究不同操作条件下液弹长度、液膜厚度与液弹速度。模拟结果用Dore等[19]的实验结果进行验证。
2 数值模型与算法 2.1 控制方程使用计算流体学(CFD)Fluent(16.2)软件进行数值模拟,选择由Hirt和Nichols[22]提出的VOF多相流模型追踪不相溶两液体的界面。VOF多相流模型的控制方程如下:
连续性方程:
| $ \frac{{\partial \rho }}{{\partial t}} + \nabla \cdot \left( {\rho \vec v} \right) = 0 $ | (1) |
动量方程:
| $ \frac{{\partial \left( {\rho \overrightarrow v } \right)}}{{\partial t}} + \nabla \cdot \left( {\rho \overrightarrow v \overrightarrow v } \right) =- \nabla P + \nabla \cdot \left[{\mu \left( {\nabla \overrightarrow v + {{\left( {\nabla \overrightarrow v } \right)}^T}} \right)} \right] + \rho \overrightarrow g + \overrightarrow F $ | (2) |
体积分数方程:
| $ \frac{{\partial {\alpha _\text{d}}}}{{\partial t}} + \overrightarrow v \cdot \nabla {\alpha _\rm{d}} = 0 $ | (3) |
流体物理性质方程:
| $ \rho = {\alpha _{\rm{c}}}{\rho _{\rm{c}}} + {\alpha _{\rm{d}}}{\rho _{\rm{d}}}\;\;\;\;\;\;\;\;\mu = {\alpha _{\rm{c}}}{\mu _{\rm{c}}} + {\alpha _{\rm{d}}}{\mu _{\rm{d}}} $ | (4) |
毛细管中流体流动为层流,界面张力与壁面吸附力占主导作用,Fluent中界面张力模型是由Brackbill等[23]提出的连续表面力(CSF)模型,VOF模型中附加的界面张力导致了动量方程中的源项。因此,动量方程中的源项为:
| $ \bar F = \sigma \left[ {\frac{{\rho \kappa \hat n}}{{\left( {1/2} \right)\left( {{\rho _{\text{c}}} + {\rho _{\text{d}}}} \right)}}} \right] $ | (5) |
| $ \hat n = \frac{n}{{\left| n \right|}}\;\;\;\;\;\;\;n = \nabla {\alpha _{\rm{d}}} $ | (6) |
| $ \kappa = \nabla \cdot \hat n $ | (7) |
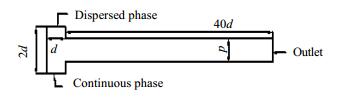
以往研究中均有使用二维与三维模型,当管道横截面为矩形时通常使用三维模型研究管道中两相流的流动情况[24, 25]。且Qian等[5]和Cherlo等[25]的研究均发现分散相弹长在二维和三维模型中没有很大差异,但三维模型中的压降大约是二维模型的两倍。本文主要讨论圆形管道中液弹长度,液膜厚度与液弹速度,所以为了节省运算时间,采用二维模型。使用GAMBIT软件构造几何模型并进行网格划分。图 1为使用T型管的几何模型简图。
|
图 1 毛细管几何模型简图 Fig.1 Schematic diagram of the geometric model of the capillary (d: diameter of capillary) |
两相入口为速度入口边界条件,出口处设为压力出口边界[26]且为标准大气压。壁面为无滑移边界条件,壁面接触角为180°。分散相入口αd=1,即该处全为分散相,连续相入口αc=1即该处全为连续相。连续相先充满管道,当t=0时,两相液体同时流入管道。所用流体的物理性质如表 1。
| 表 1 流体的物理性质 Table 1 Physical properties of the fluids studied |
采用四种均匀正方形网格划分方式,边长分别为20、12.5、10、8 μm,对应网格数分别为4100、10496、16400、25650.
2.4 数值方法使用基于压力的非稳态求解器,不考虑重力作用的影响。连续相为[C4mim][NTf2]离子液体,分散相为水。空间离散化梯度选择更准确的基于节点的格林-高斯方法[16]。压力项关联采用交错压力格式(PRESTO!),流场采用压力与速度耦合的PISO方法,动量方程选择二阶迎风格式。时间步长取1×10-5 s, 为了保证计算收敛,连续性方程的残差绝对收敛标准在10-5以内,速度残差绝对收敛标准为10-4。
3 结果与讨论T型管道直径d=0.2 mm,为了形成液弹且使流动充分发展,管长与直径比值的最小值应为40[27]。因此,管道长度设为40 d。分散相流量从0.13~1.2 mL·h-1变化,连续相流量从0.2~0.8 mL·h-1变化,根据Tsaoulidis等[28]的两相流型图可知,流动在弹状流范围内。
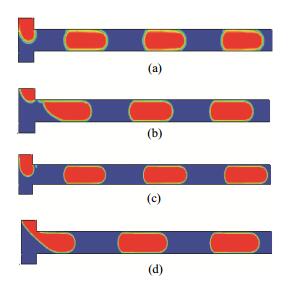
3.1 网格独立性检查图 2表示不同网格数时分散相体积分数图。由图 2可知,仅在界面处发生显著的差异,分辨率越高,界面越清晰。发现网格数为16400时交界面分布良好,过渡自然,没有明显差异。网格数为4100、10496、16400、25650(Qd=Qc=0.8 mL·h-1)对应的液弹速度分别为0.0153、0.0159、0.0159、0.0159 m·s-1,对应的液弹长度分别为0.463、0.467、0.490、0.484 mm。液弹长度与液弹速度几乎与网格分辨率无关。本文使用的网格数为16400,网格划分如图 3所示。
|
图 2 不同网格数时分散相体积分数分布图 Fig.2 Contours of the dispersed phase volume fractions at different mesh numbers (R=0.1 mm, Qd=Qc=0.8 mL·h-1) Mesh numbers (a) 4100 (b) 10496(c) 16400 (d) 25650 |

|
图 3 局部网格划分图 Fig.3 Localized mesh graph |
Garstecki等[29]发现液弹的形成有“挤压”和“剪切”两种机理,两种机理的临界毛细管数(Ca)约为10-2,本文Ca包含临界Ca,即低毛细管数时为挤压机理,刚产生的液弹进入主通道且不断增长直到几乎占满通道横截面,连续相的压力在液弹上游积聚,使得液弹在下游延长。当毛细管数增大时为剪切机理,分散相的剪切力也促使了液弹的断裂。
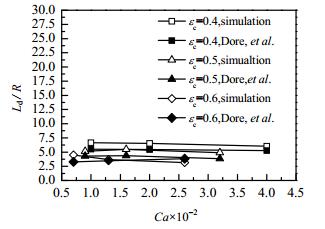
图 4为三种不同连续相流量分数下无量纲液弹长度与毛细管数(Ca)的关系,由图可知低速时,无量纲液弹长度随Ca的增大略有不同,但随Ca进一步增大趋于减小。且无量纲液弹长度随连续相流量分数的增大而减小。模拟结果与Dore等[19]的实验结果总体一致。
|
图 4 三种不同连续相流量分数下无量纲液弹长度 Fig.4 Dimensionless slug length as a function of Ca under three different flow fractions of the continuous phase |
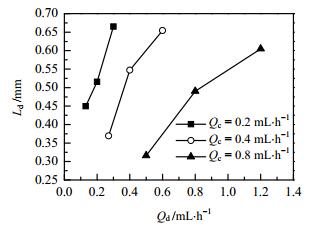
连续相流率不变,改变分散相流率,观察液弹长度变化。图 5为分散相流率对液弹长度的影响,当连续相流率为常数时,液弹长度随分散相流率的增加而变长。且由3.2.1节知,液弹长度随连续相流率增加而减小。
|
图 5 分散相流率对液弹长度影响 Fig.5 Effects of dispersed phase flow rates on slug length |
关于弹长的关系式大部分来源于气液弹状流[5, 17, 30]。有些关于液液弹状流液弹长度[20, 29, 31]的研究。Tsaoulidis等[20]提出的液弹长度关系式只适用于较大毛细管数(0.03~0.18),该毛细管数远远大于本文所用毛细管数。实际上,液弹长度受两方面影响:一是受两相流率比Qd/Qc影响的界面断裂,二是受连续相毛细管数影响的界面张力与连续相剪切力之间的平衡[31]。因此,根据模拟结果提出液弹长度的估测式:
| $ \frac{{{L_\rm{d}}}}{R} = \left( {1.263 + 1.981 \times \frac{{{Q_\rm{d}}}}{{{Q_\rm{c}}}}} \right)C{a_\rm{c}}^{-0.0891} $ | (8) |
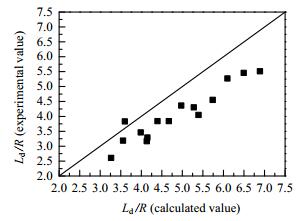
为了验证模拟结果的正确性,将式(8)的计算结果与Dore等[19]的实验值进行比较如图 6, 计算值与实验值的平均误差在20%左右。偏差较大的原因可能是实验中接触角不明确,且模拟中假设壁面光滑无滑移,与实验条件有一定的差异所致。
|
图 6 模拟结果与实验值比较 Fig.6 Comparison of simulated and experimental values |
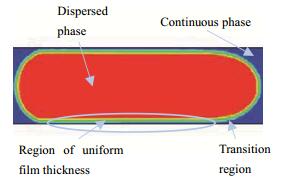
如图 7所示,在液液弹状流中,分散相液弹几乎占据了整个毛细管的横截面积,这使连续相形成薄液膜将分散相液弹与管壁分隔。分散相前端和后端为半球形,液膜沿分散相液弹长度分布不均匀,分为均匀液膜区和过渡区,本文研究均匀液膜区液膜厚度。采用FLUENT后处理软件,选取分散相体积分数为0.1的界面,即该界面处几乎全部为水相,计算液膜厚度。
|
图 7 液膜沿液弹长度分布图 Fig.7 Liquid film distribution along slug length |
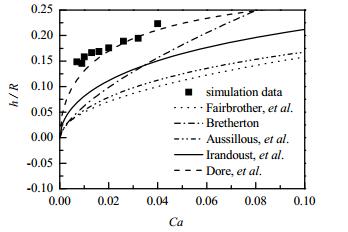
Bretherton[13]发现液膜厚度与毛细管数(Ca)有关,且随毛细管数增大而变厚。图 8为模拟的无量纲液膜厚度与Ca的关系,且模拟数值与文献中的液膜计算公式进行比较。可以发现模拟液膜厚度与Dore等[19]的模型吻合很好,平均误差约为11%。但Fairbrother等[14]、Bretherton[13]、Aussillous等[15]和Irandoust等[12]模型计算的液膜厚度远远小于模拟数据。这是可以理解的,因为这些模型是在气液弹状流的基础上总结的,气液弹状流与液液弹状流主要差异是两相黏度差,在气液弹状流中,分散相气体的黏度可以忽略,因此对界面的剪切力也可以忽略。然而,在液液弹状流中两相黏度差减小意味着两相界面剪切力的增大,这导致液膜区不可忽略的流动,因此液弹速度、液膜厚度与气液弹状流不同[32]。
|
图 8 无量纲液膜厚度与Ca关系且与文献模型比较 Fig.8 Dimensionless film thickness as a function of Ca and its comparison with literature models |
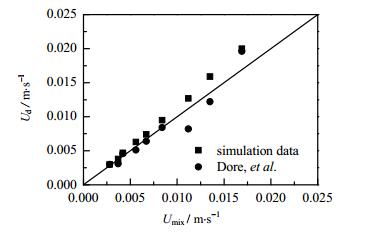
由于液弹速度与停留时间有关,所以它是传质过程中一个重要参数。毛细管中的弹状流,由于连续相液膜的存在,液弹或气泡并不能完全占据管道横截面积,这使得液弹速度总比混合速度大[20]。图 9为模拟液弹速度与混合速度关系图。由图可知模拟液弹速度与Dore等[19]的实验值整体上吻合很好。
|
图 9 液弹速度与混合速度关系 Fig.9 Relationship between slug velocity and mixing velocity |
本文模拟了不同混合速度下的液弹速度,因此,液弹的速度可由下式进行估算:
| $ {U_{\rm{d}}} = 1.157{U_{\operatorname{mix} }} $ | (9) |
为了验证该式的准确性,将式(9)的计算值与Dore等[19]的实验值对比如图 10,实验值与式(9)计算值整体吻合很好,平均误差在17.7%左右。且液弹速度与混合速度差随混合速度的变大而增大。
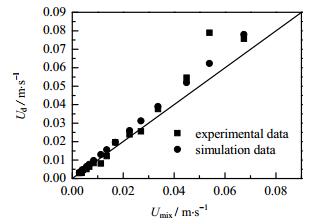
|
图 10 液弹速度实验值与公式(9)计算值比较 Fig.10 Comparison of slug velocities of experimental and calculated values (Equation (9)) |
使用计算流体力学(CFD)的方法,采用VOF多相流模型,使用水和[C4mim][NTf2]离子液体两相流体研究毛细管中液液弹状流的流体力学特性,得出结论如下:
(1) 液弹长度与两相流率和毛细管数有关,液弹长度随分散相流率的增大而增大,随连续相流率的增大而减小。不同分散相流量分数下,低速时,无量纲液弹长度随Ca的增大略有不同,但随Ca进一步增大趋于减小。
(2) 液膜厚度受毛细管数的影响且随毛细管数的增大而变厚,液膜厚度与现有的关联式符合较好,平均误差大约为11%。
(3) 由于液膜的存在,液弹速度高于混合速度,且液弹速度与混合速度的差异随混合速度的增大而增大。根据模拟数值提出关于计算液弹长度与液弹速度的关联式与实验值吻合性较好,平均误差分别约为20%,17.7%。
符号说明:
| Ca | —毛细管数( |
Ud | —液弹速度,m·s-1 |
| Cac | —连续相毛细管数( |
Umix | —混合速度,m·s-1 |
| d | —毛细管直径,m | α | —体积分数 |
| F | —体积力,N | εc | —连续相流量分数( |
| g | —重力加速度,m·s-2 | κ | —曲率,m-1 |
| h | —液膜厚度,m | μ | —黏度,Pa·s |
| Ld | —液弹长度,m | ρ | —密度,Kg·m-3 |
| —界面法线 | σ | —界面张力,N·m-1 | |
| P | —压力,Pa | 下标 | |
| Q | —体积流率,mL·h-1 | c | —连续相 |
| R | —毛细管半径,m | d | —分散相 |
| t | —时间,s | mix | —混合物 |
| [1] | DUAN Qi-rong (段岐荣). The preparation and application of capillary liquid columns (毛细管液相色谱柱的制备与应用)[D]. Zhengzhou (郑州): Zhengzhou University (郑州大学), 2010. |
| [2] | LIANG Xiao-guang(梁晓光), ZHENG Yang(郑扬), XU Song-lin(许松林). CFD modelling for gas-liquid two phases taylor flow in capillary(毛细管内气液两相流的CFD模拟)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报) , 2010, 24(3): 370-375. |
| [3] | Shao N, Salman W, Gavriilidis A, et al. CFD simulations of the effect of inlet conditions on Taylor flow formation[J]. International Journal of Heat and Fluid Flow , 2008, 29(6): 1603-1611. DOI:10.1016/j.ijheatfluidflow.2008.06.010. |
| [4] | Goel D, Buwa V V. Numerical simulations of bubble formation and rise in microchannels[J]. Industrial & Engineering Chemistry Research , 2009, 48(17): 8109-8120. |
| [5] | Qian D, Lawal A. Numerical study on gas and liquid slugs for Taylor flow in a T-junction microchannel[J]. Chemical Engineering Science , 2006, 61(23): 7609-7625. DOI:10.1016/j.ces.2006.08.073. |
| [6] | Antony R, Nandagopal M S G, Sreekumar N, et al. Liquid-liquid slug flow in a microchannel reactor and its mass transfer properties-a review[J]. Bulletin of Chemical Reaction Engineering & Catalysis , 2014, 9(3): 207-223. |
| [7] | Ghaini A, Mescher A, Agar D W. Hydrodynamic studies of liquid-liquid slug flows in circular microchannels[J]. Chemical Engineering Science , 2011, 66(6): 1168-1178. DOI:10.1016/j.ces.2010.12.033. |
| [8] | Gupta R, Leung S S Y, Manica R, et al. Hydrodynamics of liquid-liquid Taylor flow in microchannels[J]. Chemical Engineering Science , 2013, 92(14): 180-189. |
| [9] | Jovanović J, Zhou W, Rebrov E V, et al. Liquid-liquid slug flow:hydrodynamics and pressure drop[J]. Chemical Engineering Science , 2011, 66(1): 42-54. |
| [10] | Kashid M N, Agar D W. Hydrodynamics of liquid-liquid slug flow capillary microreactor:flow regimes, slug size and pressure drop[J]. Chemical Engineering Journal , 2007, 131(1-3): 1-13. DOI:10.1016/j.cej.2006.11.020. |
| [11] | Sarrazin F, Loubière K, Prat L, et al. Experimental and numerical study of droplets hydrodynamics in microchannels[J]. AIChE Journal , 2006, 52(12): 4061-4070. DOI:10.1002/(ISSN)1547-5905. |
| [12] | Irandoust S, Anderson B. Liquid film in Taylor flow through a capillary[J]. Industrial & Engineering Chemistry Research , 1989, 28(11): 1684-1688. |
| [13] | Bretherton F. The motion of long bubbles in tubes[J]. Journal of Fluid Mechanics , 1961, 10(2): 166-188. DOI:10.1017/S0022112061000160. |
| [14] | Fairbrother F, Stubbs A E. Studies in electroendosmosis:the bubble method of measurement[J]. Journal of the Chemical Society , 1935, 1: 527-529. |
| [15] | Aussillous P, Quéré D. Quick deposition of a fluid on the wall of a tube[J]. Physics of Fluids , 2000, 12(10): 2367-2371. DOI:10.1063/1.1289396. |
| [16] | Gupta R, Fletcher D F, Haynes B S. On the CFD modelling of Taylor flow in microchannels[J]. Chemical Engineering Science , 2009, 64(12): 2941-2950. DOI:10.1016/j.ces.2009.03.018. |
| [17] | Laborie S, Cabassud C, Durand-Bourlier L, et al. Characterisation of gas liquid two-phase flow inside capillaries[J]. Chemical Engineering Science , 1999, 54(23): 5723-5735. DOI:10.1016/S0009-2509(99)00146-3. |
| [18] | WEI Li-juan(魏丽娟), FU Tao-tao(付涛涛), ZHU Chun-ying(朱春英), et al. Measurement and correlation of pressure drop of liquid-liquid two-phase flow in microchannels(微通道内液液两相流压力降的测量和关联)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报) , 2013, 27(14): 555-560. |
| [19] | Dore V, Tsaoulidis D, Angeli P. Mixing patterns in water plugs during water/ionic liquid segmented flow in microchannels[J]. Chemical Engineering Science , 2012, 80(10): 334-341. |
| [20] | Tsaoulidis D, Angeli P. Effect of channel size on liquid-liquid plug flow in small channels[J]. AIChE Journal , 2016, 62(1): 315-324. DOI:10.1002/aic.15026. |
| [21] | Ghaini A, Kashid M N, Agar D W. Effective interfacial area for mass transfer in the liquid-liquid slug flow capillary microreactors[J]. Chemical Engineering and Processing:Process Intensification , 2010, 49(4): 358-366. DOI:10.1016/j.cep.2010.03.009. |
| [22] | Hirt C W, Nichols B D. Volume of fluid (VOF) method for the dynamics of free boundaries[J]. Journal of Computational Physics , 1981, 39(1): 201-225. DOI:10.1016/0021-9991(81)90145-5. |
| [23] | Brackbill J U, Kothe D B, Zemach . A continuum method for modeling surface tension[J]. Journal of Computational Physics , 1992, 100(2): 335-354. DOI:10.1016/0021-9991(92)90240-Y. |
| [24] | Raj R, Mathur R, Buwa V V. Numerical simulations of liquid-liquid flows in microchannels[J]. Industrial & Engineering Chemistry Research , 2010, 49(21): 10606-10614. |
| [25] | Cherlo S K R, Kariveti S, Pushpavanam S. Experimental and numerical investigations of two-phase (liquid-liquid) flow behavior in rectangular microchannels[J]. Industrial & Engineering Chemistry Research , 2009, 49(2): 893-899. |
| [26] | Kashid M N, Renken A, Kiwi-Minsker L. CFD modelling of liquid-liquid multiphase microstructured reactor:Slug flow generation[J]. Chemical Engineering Research and Design , 2010, 88(3): 362-368. DOI:10.1016/j.cherd.2009.11.017. |
| [27] | Talimi V, Muzychka Y S, Kocabiyik S. A review on numerical studies of slug flow hydrodynamics and heat transfer in microtubes and microchannels[J]. International Journal of Multiphase Flow , 2012, 39: 88-104. DOI:10.1016/j.ijmultiphaseflow.2011.10.005. |
| [28] | Tsaoulidis D, Dore V, Angeli P, et al. Flow patterns and pressure drop of ionic liquid-water two-phase flows in microchannels[J]. International Journal of Multiphase Flow , 2013, 54(3): 1-10. |
| [29] | Garstecki P, Fuerstman M J, Stone H A, et al. Formation of droplets and bubbles in a microfluidic T-junction-scaling and mechanism of break-up[J]. Lab Chip , 2006, 6(3): 437-446. DOI:10.1039/b510841a. |
| [30] | Liu H, Vandu C O, Krishna R. Hydrodynamics of taylor flow in vertical capillaries:flow regimes, bubble rise velocity, liquid slug length, and pressure drop[J]. Industrial & Engineering Chemistry Research , 2005, 44(14): 4884-4897. |
| [31] | Xu J H, Li S W, Tan J, et al. Correlations of droplet formation in T-junction microfluidic devices:from squeezing to dripping[J]. Microfluidics and Nanofluidics , 2008, 5(6): 711-717. DOI:10.1007/s10404-008-0306-4. |
| [32] | Eain M M G, Egan V, Punch J. Film thickness measurements in liquid-liquid slug flow regimes[J]. International Journal of Heat and Fluid Flow , 2013, 44(44): 515-523. |




