2. 浙江大学 城市学院,浙江 杭州 310015
2. Zhejiang University City College, Hangzhou 310015, China
在各种空气分离装置中,以深冷精馏技术为核心的深冷空分是生产大规模、高纯度气液相产品的主要方法。在运行过程中的电费成本占生产成本75%以上[1],美国能源情报署2014年发布的电力消耗数据表明,深冷空分行业耗电量约占美国整个工业用电量的2.2%[2];空分的下游行业包括冶金、石化和航空航天等,2018年冶金和化工等传统产业对工业气体的需求占比超过60%[3];医药、汽车等产业的工业气体需求较小,但是对气体品质要求高;民用领域如食品行业等对不同气液产品的需求量以及品质要求也各不相同[4]。基于上述因素,空分系统在运行过程中由于气体产品贮存能力有限,利润及目标组成在不断变化,因此在能源紧张和产品需求多元化的背景下,如何迅速响应外界变化是提高空分企业竞争力的唯一方法,企业不仅要考虑产品量还要考虑产品种类变化,并按电价波动对生产计划进行调整。因此同一套装置中不断响应时变电价,满足下游多种类、多变化的市场需求成为空分系统动态模拟与优化工作的推手[5-6]。换句话说,向敏捷和灵活的流程过渡是空分装置乃至整个制造业的一个不可避免的趋势。
精馏单元作为空分装置流程运行的关键设备,塔中持液量大,动态特征明显,是流程动态运行的关键设备。本文以空分系统中的精馏单元作为研究对象,通过对比讨论学者在动态过程中的控制、优化、调度、仿真问题的研究,总结在研究过程中应用的动态模型以及求解算法并提出了如下框架。
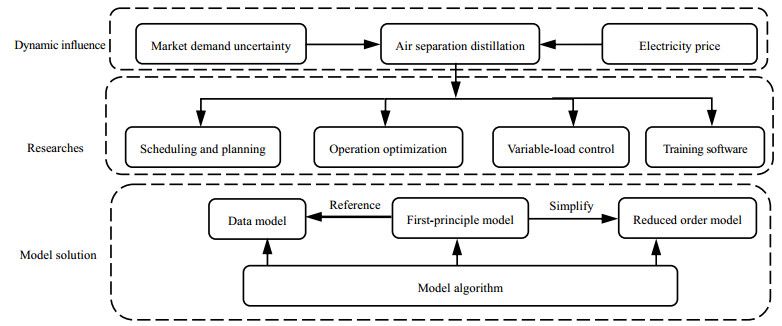
|
图 1 精馏塔动态行为研究内容框架 Fig.1 Framework of research on distillation column dynamic performance |
典型的深冷精馏空气分离装置如图 2所示,包括高压塔、低压塔、主换热器、压缩机组和粗氩塔等多个部分,经预处理工段除去杂质后的空气通过压缩机组压缩到一定压力,部分气体膨胀至液化温度并在主换热器中与液体产品换热,进入高压塔精馏,塔釜得到富氧液空送入低压塔继续精馏分离,塔顶液氮过冷节流后去低压塔塔顶回流。低压塔顶产出纯氮气,塔釜产出液氧,侧线采出粗氩气送入粗氩塔单元。运行过程中精馏塔和换热器有能量耦合,高低压塔物流也高度耦合,结构复杂,因此深冷空分在动态切换的同时兼顾产品质量殊为不易。如何快速且准确实现精馏单元动态操作分析成为空分装置优化动态行为的研究重点[7]。
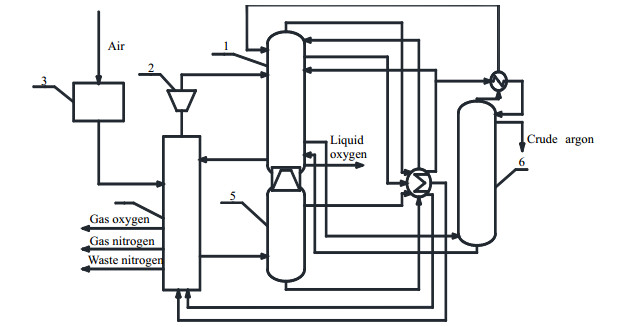
|
图 2 深冷空分过程简化流程图 Fig.2 Schematic diagram of cryogenic air separation processes 1. low pressure column 2. expander 3. compression and pre-purification 4. primary heat exchanger 5. high pressure column 6. crude argon column |
常规深冷空分精馏单元通常由2~3个精馏塔组成[8],每个精馏塔的理论塔板数在40~80块[9],每块塔板的组成成分各不相同;为了减少能耗,各个塔之间存在多个进料口和侧线出料口进行能量耦合[8-10],所以精馏塔具有大规模、强耦合、非线性的特征。国内外对空分系统中精馏单元设计和操作过程的动态行为展开研究,按照精馏塔操作过程中时间尺度可以将研究方向分为如下4类:过程变负荷控制、过程操作优化、过程调度规划和仿真软件培训系统。
2.1 过程变负荷控制在空分装置中,一旦气体需求频繁变化,如果不能及时调整生产负荷,只能放空多余产品,加重了企业的生产成本。因此空分装置的变负荷生产开始成为解决这一问题的主流措施。但是精馏单元中设备耦合多,能量和质量集成非常紧密,不能仅针对单一的精馏塔进行控制,且常规精馏塔只能在5%的设定值范围内改变操作条件,市场需求和电价的波动使得空分精馏塔的生产负荷有大范围的波动(75%~105%) [11];同时精馏塔前的压缩机组的动态行为也会使得精馏塔在操作范围内表现出非线性特性,目前基于比例积分微分(proportional integral differential,PID)的控制方案已经满足不了过程变负荷的控制要求[9];这就要求控制策略从传统小范围的线性控制向满足变负荷控制要求的非线性控制转变[12-13],因此针对变负荷过程设计控制结构和非线性控制技术是主要研究方向。
空分精馏系统作为高维大系统,控制系统结构设计是否能够满足动态过程控制至关重要,许锋等[14]提出了一种将大系统分解为子系统的划分搜索算法,在此基础上设计了合理的控制系统结构。TRIERWEILER等[15-16]提出通过鲁棒性能参数(robust performance number,RPN)来衡量控制系统的结构是否能够满足动态过程控制,并介绍了其在空分设备可控性分析中的应用。自动变负荷控制技术是快速实现变负荷生产的关键[17-18]。国内外均有空分公司实现自动变负荷生产案例[19-20]。自动变负荷控制主要是通过流程设计和优化控制来实现,其基本设计思路可以概括为:流程计算、确定关键变量、建立动态模型及控制方案、模型参数修正四个步骤[21]。自动变负荷技术的核心是模型预测控制,其中的难点是如何建立合适的动态模型描述变负荷过程。XU等[11]提出了一个操作轨迹线性参数变化(line parameter varying, LPV)模型描述空分过程的非线性动态行为,在此基础上设计了非线性模型预测控制器,通过多变量模型预测策略控制低温空气分离过程。BIAN等[22]利用非线性波模型设计了氮气纯化塔的非线性模型预测控制器,并将控制器的模拟结果和传统的PID控制器进行对比,结果显示对空分系统中复杂的三塔装置,预测控制显得较为合适。ROFFEL等[23]基于动态机理模型提出的多变量预测模型对精馏塔实现了良好的预测能力。李华银等[24]提出了一种多变量预测控制策略,实现了空分装置的自动变负荷控制。
2.2 过程动态优化随着外界影响越来越频繁,空分系统中的精馏塔长期处于动态变化之中,如何在变负荷过程中迅速找到一个最优操作条件,已成为研究热点之一。其实质就是通过决定动态系统中的控制变量,使系统中的某性能指标达到最优[18]。空分系统中精馏单元的操作优化对象是3个耦合塔组,以某一性能指标为目标函数,过程模型中的物料能量衡算和基本性质方程作为约束条件。优化命题中的目标函数和部分约束条件通过微分-代数方程组(differential-algebraic equations,DAEs)进行描述,由于变量数目多,模型非线性强,且需要考虑电价和需求的不确定性带来的影响。所以在动态优化过程中,如何构建动态过程操作优化命题?如何提高大尺度方程组的计算效率?如何从离线优化转变为在线实时优化?等方法论仍然是研究的主要难点和热点。
ZHU等[25]建立了空分精馏单元严格的非线性模型,模型中考虑了电价的变化和产品需求的不确定性,在此基础上对空分精馏装置进行了生产优化。但是基于机理模型的优化命题不仅含有大量的非线性方程,甚至还存在变负荷约束条件,由于求解这一问题需要消耗的时间较长[26],ZHU等[27]进一步将优化命题的结构进行内部分解,提高求解效率。动态优化问题需要及时调整至最优的操作条件,因此实时优化(real time optimization,RTO)技术[18, 28-29]应运而生。王凯等[30]收集了空分装置运行过程中的各种工况,建立了动态数据库对大型空分装置的变负荷操作进行优化,将计算机技术融入工业过程优化问题求解过程中。SIRDESHPANDE等[31]采用数据模型大大减少了不同工况下最佳操作条件的决策时间。但是,在空分系统中,精馏单元的动态特性和复杂机理模型使得RTO技术在求解操作优化问题的稳定性和实时性上存在难点。ZHU等[32]提出了一种同伦回溯算法(homotopy based backtracking method,HBM)解决了深冷精馏空分系统中的变负荷操作优化问题中计算效率低、可行域分析困难等问题,解决了深冷空分系统中RTO计算的关键问题。
2.3 过程调度规划针对下游用气企业中不确定的产品需求和上游电价的调节,供应链上游的空分企业将气体产品和下游的产品需求进行合理配置,就能降低运行费用。常规地,在企业内部,通常由工程师结合个人经验得出调度的方案,得到的结果主观性强、难以实现最优配置。常见的3种调度形式分别是工厂间的生产调度、工厂单一装置生产负荷规划和工厂产量规划,其本质是混合整形非线性规划问题。当前空分精馏系统中的调度研究主要可以分为建立调度框架和建立过程动态模型。
PATTISON[5]和JOHANSSON[33]针对快速变化的电力市场,分别建立了空分系统的最佳工艺操作条件的调度框架和工厂调度决策框架。CAO等[34-35]在此基础上考虑了产品需求对空分系统的影响,并使用工厂历史数据对调度参数进行调整。TOURETZKY等[36]提出了一种新型的空分过程综合调度和动态优化框架应对电价影响,同时根据历史数据提出了空分系统的低阶动态模型,捕捉调度相关变量的动态变化,使用该模型提出了空分过程中调度和控制一体化的集成公式,框架中考虑的实时电价信息,提高了空分装置的利润。PATTISON等[37]在动态模型的基础上提出了新型移动边界闭环调度方法,在空分过程实现了利润最大化,同时产量和纯度能在短时间内发生变化。近几年,随着MISRA等[38]提出的基于状态任务网络(state task network,STN)的调度框架,调度问题可以进行更为细致的描述,在改进决策方面获得了更好的结果。
在考虑调度框架的同时,部分研究者还针对调度规划问题的模型进行了研究。IERAPETRITOU等[39]建立简化机理模型, 求解能耗最低下的生产调度方案。但是上述机理模型非线性强,求解时间长,因此基于数据建立代理模型的研究越来越多。KARWAN等[40]基于少数操作数据,提出了通过优化嵌入在滚动时域方法的混合整数规划(mixed integer linear programming,MILP)问题来获得电价变化条件下的计划决策。MITRA等[41]基于代理模型建立离散时间下的MILP命题,对操作模式之间的转换进行准确有效的模拟,从而实现运营过程中的生产计划最优。ZHANG等[42]和ZHOU等[43-44]分别基于数据建立了凸包代理模型,对装置在不同负荷和切换过程进行详细描述,最终建立了联产调度MILP命题。但下游需求的多样化导致的不确定性需要更加详细、多维的模型进行描述。
2.4 过程仿真培训系统在上述3类问题的驱动下,越来越多的企业和研究机构开始着手开发动态行为下的空分仿真模拟软件[45-46]。仿真培训系统可以为设备及控制系统设计提供依据;对多种控制方案进行优选;代替实际实验装置对操作给出动态响应,为后续开发仿真系统提供基础[47-49]。
目前国内基于空分背景下的仿真模拟软件主要有两类:一种是模拟整个空分系统的操作仿真[45-46, 50]。另一种是针对空分系统中特定的操作单元开发的仿真[51-53]。上述两类软件都是基于机理模型进行仿真,由于机理模型非线性程度高,需要针对模型开发求解算法,往往存在难收敛、精度低、鲁棒性差的缺陷。现有的仿真软件中大部分使用简化机理模型,鲜有全面考虑变负荷等动态情况,很难满足精度要求,因此后续的动态优化、变负荷控制、调度的动态仿真仍受到一定限制。
3 空分精馏系统动态建模综上所述,无论是过程变负荷控制、过程操作优化、过程调度规划还是过程仿真培训系统开发,如何建立一个数学模型能够准确地描述系统稳态运行过程,及时捕获其动态行为成为难点之一。精馏过程的数学模型根据过程变量是否随时间变化可以分为稳态模型和动态模型,稳态模型以代数方程形式描述了过程中变量不随时间变化的关系,而动态模型则以微分方程形式描述过程中变量随时间变化的关系。针对空分系统精馏单元的不同动态问题,其目标是建立合适精度的模型。研究者建立的动态模型主要分为机理模型和数据模型,但是由于空分精馏单元的机理模型过于复杂,计算过程冗长;数据模型又缺少物理意义,不宜大范围外推,所以部分研究者在此基础上建立了降阶模型,3类模型的主要特征如表 1所示。
|
|
表 1 动态模型主要特征 Table 1 Main characteristics of dynamic models |
机理模型法是针对精馏塔建模的传统方法,这一模型是由塔中物料、能量平衡方程以及物理性质的平衡关系推导实现[25, 54],既可以描述稳态过程,也可以运用在动态过程中。在动态机理模型中物料、能量平衡方程为微分形式;汽液相平衡、热力学和水力学等物理性质方程是代数形式,从而构成了DAEs对精馏塔的动态行为进行描述。精馏塔的基本动态机理模型可以写成如下通用形式:
总质量平衡:
| $\frac{{{\rm{d}}{M_j}}}{{{\rm{d}}t}} = {L_{j - 1}} + {V_{j + 1}} - {L_j} - {V_j} + {F_j}$ | (1) |
组分i的物料平衡
| $\frac{{{\rm{d}}{M_j}{x_{i, j}}}}{{{\rm{d}}t}} = {L_{j - 1}}{x_{i, j - 1}} + {V_{j + 1}}{y_{i, j + 1}} - {L_j}{x_{i, j}} - {V_j}{y_{i, j}}$ | (2) |
能量平衡:
| $\frac{{{\rm{d}}{U_j}}}{{{\rm{d}}t}} = {L_{j - 1}}h_{j - 1}^l + {V_{j + 1}}h_{j + 1}^v - {L_j}h_j^l - {V_j}h_j^v + {Q_j}$ | (3) |
体积约束方程:
| $\frac{{M_j^l}}{{\rho _j^l}} + \frac{{M_j^{\rm{v}}}}{{\rho _j^{\rm{v}}}} = {V_j}$ | (4) |
相平衡方程:
| ${y_{i, j}} = {k_{i, j}}{x_{i, j}}$ | (5) |
归一化方程:
| $\sum\limits_{i = 1}^c {{x_{i, j}}} {\rm{ = }}\sum\limits_{i = 1}^c {{y_{i, j}}} = 1$ | (6) |
水力学方程:
| ${L_j}{\rm{ = }}f\left( {\rho _j^l, M_j^l} \right), {V_j}{\rm{ = }}g\left( {\rho _j^l, \rho _j^{\rm{v}}, M_j^l, M_j^{\rm{v}}} \right)$ | (7) |
机理模型的适用范围很广,通常在控制器设计、控制策略分析和操作优化时,均需要以严格机理模型为基础。例如在设计多变量控制器时,必须使用严格的非线性机理模型来捕获运行过程中设备间的相互作用,从而对其进行有效的控制。对此ROFFEL等[23]提出了严格的机理模型。同时,当需要提出一种新模型用于稳态优化和动态优化时,机理模型准确性高,可以作为任何控制器实施的基准,用于评估非线性波模型的预测能力。BANSAL等[55]开发了一种新的多组分混合整数动态精馏塔模型。MILLER等[56]开发了深冷空分设备的详细开车模型。GUO等[57]基于深冷精馏塔的机理模型讨论了几个质量流量阶跃变化下上下塔的动态特性。但是动态过程的机理模型具有高维度、非线性、离散化等特点,所以在求解DAEs过程中需要足够的计算时间且容易收敛失败,很难在线预测需求变化后的优化操作。
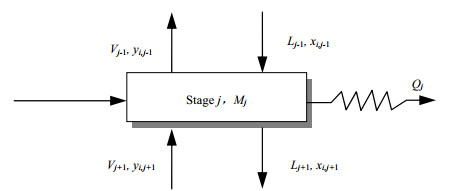
|
图 3 精馏塔平衡级理论模型示意图 Fig.3 Theoretical scheme of equilibrium stage in a distillation column |
相比于复杂的机理模型,数据模型计算时间短,易于建模[58]。研究者对运行历史数据或者仿真模拟软件结果进行归纳,将精馏塔的输入、输出变量用线性或非线性关联式回归,推导得到数据模型。这在优化和规划等问题中广泛使用。
电价和产品发生变化时,工厂会采用不同工况下稳态操作的历史数据的线性关系对操作条件进行调整。但是由于电价、需求等因素变化越来越频繁,研究者开始采用实时在线优化[28, 59-60]、模型预测控制[60]等智能技术对空分系统进行优化操作和上层规划。CHIEN等[61]基于高纯塔运行过程中测温点得到的温度数据,建立了一阶形式的非线性数据模型,通过该模型设计的非线性控制器结构简单且能够适应工厂不同环境。SIRDESHPANDE等[31]在只考虑氧产品且浓度95%的情况下,建立了简单代数模型,并从机理模型的模拟结果中回归得到代数模型的参数,结果显示该模型大大减少了不同工况下最佳操作条件的决策时间。
但是运行数据准确性不佳,数据建模过程缺少明确的物理意义,导致数据模型很难捕捉精准的动态行为。一些研究者采用增加约束条件[60]、提出LPV辨识法[62-64]等手段来改进数据模型的缺陷。
3.3 降阶模型空分系统中精馏单元的机理模型具有高维度、大规模的特点[65],虽然研究人员已经开发出了许多算法[66-68],用于求解大型DAEs,但大部分算法只针对单个精馏塔进行快速有效的计算,对于多塔耦合情况就大打折扣,过大的计算量增加了计算成本。因此需要采用模型降阶、结构分解、线性近似等方法对机理模型进行必要的简化,其中降低大规模动态模型的维度一直是研究的重点。研究者通常会构建一个低阶模型来代替原始模型,在众多简化模型中,最典型的3种分别是波模型、隔室模型和配置模型[7, 22]。这3种模型均可以贴切描述系统的动态行为,又减小了计算难度,在动态仿真、在线优化、控制策略设计等领域中被广泛使用。
3.3.1 波模型精馏塔中各种类型的干扰使得塔中的组分、温度发生变化,塔中组分、温度含量曲线可以通过恒定模式的波来描述,这一曲线和数学物理学中定义的非线性波类似,基于此研究者提出了精馏塔的波模型,除了一些机理模型中的假设外,还必须假设建立的波模型具有恒定的波形。典型精馏塔中的简化波模型中的波前速度方程和组分方程分别如式(8)和(9)所示。
波模型减少计算量的同时有较为明确的物理意义,为非线性控制系统的设计奠定基础。BIAN等[69-70]先建立了高纯度精馏塔的波模型,并利用特定位置测量得到的组分/温度数据在线估计出了波模型的参数,利用非线性波模型设计了氮气净化塔的非线性模型预测控制器。ZHU等[9]基于氮气纯化分离塔中传播的波前轨迹理论,推导了描述分离塔基本动态行为的简单数学模型。塔顶的冷凝器和再沸器则使用严格的质量和能量平衡方程进行建模,并基于建立的低阶模型使用商业软件进行仿真,在大范围的操作条件下得到令人满意的预测结果。KIENLE[71]基于恒摩尔溢流的假设,分别用三元和五元组分的混合物精馏证明了低阶波模型描述的动态行为与机理模型得到的结果非常吻合。
波前速度方程:
| $\omega = \frac{{{\rm{d}}S}}{{{\rm{d}}t}} = \frac{1}{N}\frac{{ - L\left( {{x_{{\rm{in}}}} - {x_{{\rm{out}}}}} \right) + V\left( {{y_{{\rm{out}}}} - {y_{{\rm{in}}}}} \right)}}{{{n_l}\left( {{x_{{\rm{in}}}} - {x_{{\rm{out}}}}} \right) + {n_v}\left( {{y_{{\rm{out}}}} - {y_{{\rm{in}}}}} \right)}}$ | (8) |
组分方程:
| $ y\left( z \right) = {y_{{\rm{min}}}} + \frac{{{y_{{\rm{max}}}} - {y_{{\rm{min}}}}}}{{1 + {e^{\left[ { - \gamma \left( {z - S} \right)} \right]}}}} $ | (9) |
在构建一些低阶模型的过程中,研究者会采用方程线性化、设置校正因子或状态变量的方法简化模型,所以存在一定的缺陷。而隔室模型在建模过程中仅假设塔板的动态变化比整个精馏塔快,然后将塔分成几段来代替每一块塔板,每一段的动态模型是将该段中的逐板平衡与整体平衡方程相结合得到的。该模型在保留精馏塔物理化学特征的同时减少了计算变量,保证了预测精度[65]。BIAN等[22]针对深冷空分单元上塔构建了降阶动态模型,模型中应用物理坐标变换描述每个隔室的微分方程。KHOWINIJ等[72]则应用时间尺度参数将描述每个隔室的大多数常微分方程转换为更简单的代数方程而得到降阶非线性模型,并用时间离散方法产生了适合于实时求解的稀疏非线性模型预测控制(nonlinear model predictive control, NMPC)问题。CHEN[73]针对上述研究产生的稀疏特性,设计了一套非线性模型预测控制器,在线求解过程中的动态问题。在研究过程中研究者发现分割点位置的选取会大大影响模型复杂性和精度[74-75]。
3.3.3 配置模型上世纪90年代配置模型开始应用于塔分离,类似于隔室模型,配置模型也是通过选取适当数量的正交点代替全塔中的每一块塔板,只需要在正交点上构建动态平衡方程即可。但由于选择的正交点具有随机性,和塔板的位置有很大的关系,这些动态平衡方程通常是以偏微分形式表达,研究者们通过正交配置的方法推导出低阶模型。WONG等[76]使用正交配置过程建立了低阶简化模型,最终将状态方程减少到5个。CAO等[7]使用拉格朗日多项式对整个塔进行动态建模,将塔纵向细分为多个有限元,解决了低阶多项式不能准确捕捉塔内动态轨迹的缺点。结果显示该模型在稳态或动态模拟中,实现模型简化的同时,预测误差可以忽略。CHO等[77]针对精馏、吸收和萃取等分离过程,用偏微分方程组近似逐板差分方程组,通过正交配置法有效简化了多组分分离系统所需方程组。当然配置法建模也存在一些缺点,如选择的点数小于实际过程中的分离级数,塔中其他的状态变量必须通过插值确定,模型的准确性受到点数的限制;以及进料或者出料造成的塔中不连续会产生误差。
4 动态优化问题的算法研究目前研究者已经开发出了许多快速有效的算法求解各种模型,针对数据模型和降阶模型的算法较多,且在计算时间和准确性上均有大量研究,本文仅对机理模型为基础的动态优化问题求解算法进行介绍。精馏单元的动态优化问题实质是NLP命题,主要涉及到DAEs的求解[78]。DAEs是一组具有附加代数约束的微分方程组,有全隐式和半隐式两种格式,分别如式(10)和(11)所示:
| $F\left( {x, y\left( x \right), y'\left( x \right)} \right) = 0$ | (10) |
| $y'\left( x \right) = f\left( {x, y\left( x \right), z\left( x \right)} \right), 0 = g\left( {x, y\left( x \right), z\left( x \right)} \right)$ | (11) |
针对动态优化问题,目前已经有许多应用的软件,其核心是将DAEs离散化,然后用NLP求解器进行联立求解,但其弊端之一是不能针对各类动态优化问题进行灵活求解,如何提高命题求解效率和寻找合适的初值点仍然是求解空分精馏塔动态优化命题的难点。
求解DAE优化问题主要分为离散法和变分法[79]。传统的变分法一般适用于求解无约束优化问题,对于约束优化问题,求解方法基本采用离散策略。空分精馏单元的动态优化是一个超大规模的NLP问题,针对大规模的NLP问题,序列二次规划算法(sequence quadratic program, SQP)求解效率不高,但计算机技术[80]和改进的SQP算法[81-82]提高了求解速度。CUTHRELL等[83]通过多项式近似和正交配置将微分方程将使用离散化,然后将得到的代数方程编写为非线性规划(nonlinear programming,NLP)的一部分,并用SQP优化技术解决。BIEGLER等[84-85]对DAEs优化问题的同步策略算法进行改进,并在低温精馏塔中验证了求解效率。部分研究者通过空间分解策略减小问题规模,ELIK等[86]使用ADOMIAN分解法对DAEs进行求解,通过两个例子来说明该方法的有效性。
针对大规模的空分精馏塔,合适的初值点显得更为关键。一些研究者会通过先验知识得到一个合适的初值点,但更多的是通过约束算法找到一个合适的初值区域。文献[87]提出了一种基于群概率分布估计的动态优化方法,通过基于群概率分布估计法(population based probability distribution estimation,PPDE)得到的概率分布,找到一个最优解所在空间,在该区域内进行迭代,提高了求解效率。
5 结论在能源紧张和产品需求多元化的背景下,如何迅速稳定响应外界变化是提高空分企业竞争力的唯一方法。针对深冷精馏空分装置在运行过程中的动态问题,研究内容主要集中于:(1)实现变负荷控制技术;(2)提高操作过程的优化效率;(3)研究混合整形非线性规划问题;(4)建立空分精馏塔动态模型以及相应的求解算法。
借以人工智能和计算机软硬件技术的发展,如何将机理模型与数据模型有机融合从而开发更准确可靠的动态模型[88]?如何利用数据可视化技术展开空分精馏塔的性能监控、运行维护和操作评估[89]?本文提出如下两点展望。(1)结合机理模型的定性优点和数据模型的定量优点,将两者转化成统一的数学语言进行描述,实现两者的有机融合;(2)在大量工厂运行数据基础上,通过算法对数据进行可视化处理,能够及时监测各个设备的性能指标;同时通过预测技术,将事故控制在可调度范围内。
符号说明:
| F | -进料量,kmol·h-1 | ρ | -密度,kg·m-3 |
| h | -单位摩尔焓,kJ·kmol-1 | ω | -波传播速度,h-1 |
| k | -气液平衡常数 | γ | -波面斜率 |
| L | -下降液体流量,kmol·h-1 | 上标 | |
| n | -塔板持液、气量 | l | -液相 |
| N | -理论塔板数 | v | -气相 |
| M | -气、液相总摩尔数,kmol | f | -进料 |
| Q | -热负荷,kJ | 下标 | |
| S | -波形位置 | j | -塔板编号,从上往下递增 |
| U | -气、液相总能量,kJ | i | -组分编号 |
| V | -上升蒸汽流量,kmol·h-1 | in | -入塔 |
| x | -液相中某组分的摩尔分数 | out | -出塔 |
| y | -气相中某组分的摩尔分数 | min | -下限 |
| z | -沿塔的比例系数,[0, 1] | max | -上限 |
| [1] |
CHANG L, LIU X G. Modeling, characteristic analysis and optimization of an improved heat-integrated air separation column[J]. Chemical Engineering & Technology, 2015, 38(1): 164-172. |
| [2] |
U.S. Energy Information Administration. 2014 MECS Survey Data[R/OL]. 2014, [2018-09-20]. https://www.eia.gov/onsumption/manufacturing/data/2014/index.php?view=data#r13.
|
| [3] |
中国产业信息网. 2018年中国工业气体行业发展概况及发展趋势分析[EB/OL]. (2018-02-09)[2018-09-20]. www.chyxx.com/industry/201802/612505.html. China Industry Information Website. Development situation and trend analysis of China's industrial gas industry in 2018 [EB/OL]. (2018-02-09)[2018-09-20]. www.chyxx.com/industry/201802/612505.html. |
| [4] |
ZHANG X B, CHEN J Y, Yao L, et al. Research and development of large-scale cryogenic air separation in China[J]. Journal of Zhejiang University Science A (Applied Physics & Engineering), 2014, 15(5): 309-322. |
| [5] |
PATTISON R C, TOURETZKY C R, JOHANSSON T, et al. Optimal process operations in fast-changing electricity markets: Framework for scheduling with low-order dynamic models and an air separation application[J]. Industrial & Engineering Chemistry Research, 2016, 55(16): 4562-4584. |
| [6] |
PATTISON R, TOURETZKY C R, JOHANSSON T, et al. Moving horizon scheduling of an air separation unit under fast-changing energy prices[J]. IFAC-PapersOnLine, 2016, 49(7): 681-686. DOI:10.1016/j.ifacol.2016.07.257 |
| [7] |
CAO Y, SWARTZ C L E, FLORES-CERRILLO J, et al. Dynamic modeling and collocation-based model reduction of cryogenic air separation units[J]. AIChE Journal, 2016, 62(5): 1602-1615. DOI:10.1002/aic.15164 |
| [8] |
SELIGER B, HANKE-RAUSCHENBACH R, HANNEMANN F, et al. Modelling and dynamics of an air separation rectification column as part of an IGCC power plant[J]. Separation & Purification Technology, 2006, 49(2): 136-148. |
| [9] |
ZHU G Y, HENSON M A, MEGAN L. Low-order dynamic modeling of cryogenic distillation columns based on nonlinear wave phenomenon[J]. Separation & Purification Technology, 2001, 24(3): 467-487. |
| [10] |
CAO Y, SWARTZ C L E, FLORES-CERRILLO J. Preemptive dynamic operation of cryogenic air separation units[J]. AIChE Journal, 2017, 63(9): 3845-3859. DOI:10.1002/aic.15753 |
| [11] |
XU Z H, ZHAO J, CHEN X, et al. Automatic load change system of cryogenic air separation process[J]. Separation & Purification Technology, 2011, 81(3): 451-465. |
| [12] |
BEQUETTE B W. Nonlinear control of chemical processes: A review[J]. Industrial & Engineering Chemistry Research, 1991, 30(7): 1391-1413. |
| [13] |
WANG S J, YU S W. Nonlinear control of a high-purity distillation column[J]. Journal of the Chinese Institute of Chemical Engineers, 1998, 29(3): 183-192. |
| [14] |
许锋, 袁未未, 罗雄麟. 大系统结构分解的评价准则和控制系统结构设计方法[J]. 高校化学工程学报, 2018, 32(3): 606-619. XU F, YUAN W W, LUO X L. Decomposition evaluation criteria and control structure design of large-scale systems[J]. Journal of Chemical Engineering of Chinese Universities, 2018, 32(3): 606-619. DOI:10.3969/j.issn.1003-9015.2018.03.016 |
| [15] |
TRIERWEILER J O, ENGELL S. A case study for control structure selection: Air separation plant[J]. Journal of Process Control, 2000, 10(2-3): 237-243. DOI:10.1016/S0959-1524(99)00035-9 |
| [16] |
TRIERWEILER J O, ENGELL S. The robust performance number: A new tool for control structure design[J]. Computers & Chemical Engineering, 1997, 21(1-2): S409-S414. |
| [17] |
陈秋霞, 周芬芳. 空分设备自动变负荷控制技术综述[J]. 深冷技术, 2011(7): 16-20. CHEN Q X, ZHOU F F. General description of automatic variable-load control technique for air separation plant[J]. Cryogenic Technology, 2011(7): 16-20. |
| [18] |
邵之江, 方学毅, 王可心. 复杂流程系统的实时模拟与优化[M]. 北京: 科学出版社, 2014. SHAO Z J, FANG X Y, WANG K X. Real time simulation and optimization of complex process system[M]. Beijing: Science Press, 2014. |
| [19] |
VINSON D R. Air separation control technology[J]. Computers & Chemical Engineering, 2006, 30(10): 1436-1446. |
| [20] |
周芬芳, 王凯. 空分设备自动变负荷先进控制技术[J]. 深冷技术, 2009(3): 28-31. ZHOU F F, WANG K. Advanced control technology of automatic load change for air separation unit[J]. Cryogenic Technology, 2009(3): 28-31. |
| [21] |
饶汀. 浅谈空分装置的自动变负荷技术[J]. 化工技术与开发, 2017, 46(8): 37-39. RAO T. Analysis on technology of automatic load change in air separation unit[J]. Technology & Development of Chemical Industry, 2017, 46(8): 37-39. DOI:10.3969/j.issn.1671-9905.2017.08.010 |
| [22] |
BIAN S, KHOWINIJ S, HENSON M A, et al. Compartmental modeling of high purity air separation columns[J]. Computers & Chemical Engineering, 2005, 29(10): 2096-2109. |
| [23] |
ROFFEL B, BETLEM B H L, DE RUIJTER J A F. First principles dynamic modeling and multivariable control of a cryogenic distillation process[J]. Computers & Chemical Engineering, 2000, 24(1): 111-123. |
| [24] |
李华银, 赵均, 徐祖华. 多变量预测控制在空分装置自动变负荷中的应用[J]. 化工自动化及仪表, 2009, 36(4): 119-121. LI H Y, ZHAO J, XU Z H. Application of multi-variable model predictive control to automatic variable-loading of air separation unit[J]. Control and Instruments in Chemical Industry, 2009, 36(4): 64-67. DOI:10.3969/j.issn.1000-3932.2009.04.016 |
| [25] |
ZHU Y, LEGG S, LAIRD C D. A multiperiod nonlinear programming approach for operation of air separation plants with variable power pricing[J]. AIChE Journal, 2011, 57(9): 2421-2430. DOI:10.1002/aic.12464 |
| [26] |
张余岳.化工过程模拟与在线优化[D].杭州: 浙江大学, 1998. ZHANG Y Y. Chemical process simulation and real time (on-line) optimization[D]. Hangzhou: Zhejiang University, 1998. http://cdmd.cnki.com.cn/Article/CDMD-10335-2006151483.htm |
| [27] |
ZHU Y, LEGG S, LAIRD C D. Optimal operation of cryogenic air separation systems with demand uncertainty and contractual obligations[J]. Chemical Engineering Science, 2011, 66(5): 953-963. DOI:10.1016/j.ces.2010.11.039 |
| [28] |
HUANG R. Nonlinear model predictive control and dynamic real time optimization for large-scale processes[D]. Pittsburgh: Carnegie Mellon University, 2010.
|
| [29] |
WÜRTH L, HANNEMANN R, MARQUARDT W. Neighboring-extremal updates for nonlinear model-predictive control and dynamic real-time optimization[J]. Journal of Process Control, 2009, 19(8): 1277-1288. DOI:10.1016/j.jprocont.2009.02.001 |
| [30] |
王凯, 邵之江, 纪彭, 等.一种基于模板技术的空分设备变负荷优化方法: 中国, 106 295 132 A[P]. 2017-01-04. WANG K, SHAO Z J, JI P, et al. A variable load optimization method for air separation plant based on template technology: CN, 106 295 132 A[P]. 2017-01-04. |
| [31] |
SIRDESHPANDE A R, IERAPETRITOU M G, ANDRECOVICH M J, et al. Process synthesis optimization and flexibility evaluation of air separation cycles[J]. AIChE Journal, 2005, 51(4): 1190-1200. DOI:10.1002/aic.10377 |
| [32] |
ZHU L Y, CHEN Z, CHEN X, et al. Simulation and optimization of cryogenic air separation units using a homotopy-based backtracking method[J]. Separation & Purification Technology, 2009, 67(3): 262-270. |
| [33] |
JOHANSSON T. Integrated scheduling and control of an air separation unit subject to time-varying electricity prices[D]. Stockholm: KTH Royal Institute of Technology, 2015.
|
| [34] |
CAO Y, SWARTZ C L E, BALDEA M. Design for dynamic performance: Application to an air separation unit[C]//Proceedings of the 2011 American Control Conference, Piscataway: IEEE, 2011: 2683-2688.
|
| [35] |
CAO Y, SWARTZ C L E, BALDEA M, et al. Optimization-based assessment of design limitations to air separation plant agility in demand response scenarios[J]. Journal of Process Control, 2015, 33: 37-48. DOI:10.1016/j.jprocont.2015.05.002 |
| [36] |
TOURETZKY C, JOHANSSON T, PATTISON R, et al. Integrated scheduling and dynamic optimization of a cryogenic air separation unit subject to time-varying electricity prices[C]//Proceedings of the 2015 AIChE Annual Meeting, New York: Wiley-Blackwell, 2015: 399a.
|
| [37] |
PATTISON R C, TOURETZKY C R, HARJUNKOSKI I, et al. Moving horizon closed-loop production scheduling using dynamic process models[J]. AIChE Journal, 2017, 63(2): 639-651. DOI:10.1002/aic.15408 |
| [38] |
MISRA S, KAPADI M, GUDI R D, et al. Production scheduling of an air separation plant[J]. IFAC PapersOnLine, 2016, 49(7): 675-680. DOI:10.1016/j.ifacol.2016.07.256 |
| [39] |
IERAPETRITOU M G, WU A D, VIN J, et al. Cost minimization in an energy-intensive plant using mathematical programming approaches[J]. Industrial & Engineering Chemistry Research, 2002, 41(21): 5262-5277. |
| [40] |
KARWAN M H, KEBLIS M F. Operations planning with real time pricing of a primary input[J]. Computers & Operations Research, 2007, 34(3): 848-867. |
| [41] |
MITRA S, GROSSMANN I E, PINTO J M, et al. Optimal production planning under time-sensitive electricity prices for continuous power-intensive processes[J]. Computers & Chemical Engineering, 2012, 38: 171-184. |
| [42] |
ZHANG Q, GROSSMANN I E, HEUBERGER C F, et al. Air separation with cryogenic energy storage: Optimal scheduling considering electric energy and reserve markets[J]. AIChE Journal, 2015, 61(5): 1547-1558. DOI:10.1002/aic.14730 |
| [43] |
周丹艳.联产空分装置的变负荷调度研究[D].杭州: 浙江大学, 2016. ZHOU D Y. Optimal scheduling of multiple air separation units under frequently changing demands[D]. Hangzhou: Zhejiang University, 2106. http://cdmd.cnki.com.cn/Article/CDMD-10335-1016185645.htm |
| [44] |
ZHOU D Y, ZHOU K, ZHU L Y, et al. Optimal scheduling of multiple sets of air separation units with frequent load-change operation[J]. Separation and Purification Technology, 2017, 172: 178-191. DOI:10.1016/j.seppur.2016.08.009 |
| [45] |
童莉葛, 高远, 王立, 等. 空分装置操作仿真系统的研究与开发[J]. 工程科学学报, 2001, 23(4): 365-367. TONG L G, GAO Y, WANG L, et al. Research and development of the simulation system for air separation equipment[J]. Journal of University of Science and Technology Beijing, 2001, 23(4): 365-367. |
| [46] |
鲍有文, 童莉葛, 张延平, 等. 国产大型空分装置计算机操作仿真系统的开发研究[J]. 测控技术, 2003, 22(8): 48-52. BAO Y W, TONG L G, ZHANG Y P, et al. The operation simulation system for home-made large-scale air separation unit[J]. Measurement & Control Technology, 2003, 22(8): 48-52. DOI:10.3969/j.issn.1000-8829.2003.08.016 |
| [47] |
CASTRELLÓN T, BOTÍA D C, GÓMEZ R, et al. Using process simulators in the study, design, and control of distillation columns for undergraduate chemical engineering courses[J]. Computer Applications in Engineering Education, 2011, 19(3): 621-630. |
| [48] |
张治山, 王超, 张青军, 等. 基于Aspen Dynamics超精馏塔的动态模拟与控制[J]. 现代化工, 2017, 37(4): 196-199. ZHANG Z S, WANG C, ZHANG Q J, et al. Dynamic simulation and control of super fractionator based on Aspen Dynamics[J]. Modern Chemical Industry, 2017, 37(4): 190-193. |
| [49] |
朱兆友, 张方坤, 王英龙. 化工过程动态仿真的研究与应用进展[J]. 现代化工, 2013, 33(7): 118-120. ZHU Z Y, ZHANG F K, WANG Y L. Research and application development of dynamic simulation of chemical process[J]. Modern Chemical Industry, 2013, 33(7): 118-120. DOI:10.3969/j.issn.0253-4320.2013.07.032 |
| [50] |
李靖鑫.基于MWorks平台空分流程的模拟仿真[D].武汉: 华中科技大学, 2014. LI J X. Simulation and optimization of air separation unit based on Mworks[D]. Wuhan: Huazhong University of Science & Technology, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10487-1015010621.htm |
| [51] |
刘仁亮, 刘超, 魏雪琴. 大型空分设备气体压缩机组仿真平台的研发及应用[J]. 深冷技术, 2017(7): 1-12. LIU R L, LIU C, WEI X Q. Development and application of simulation platform for gas compressors set of large-sized air separation plant[J]. Cryogenic Technology, 2017(7): 1-12. |
| [52] |
刘波.基于Hysys的空分精馏过程仿真分析[D].西安: 西安电子科技大学, 2013. LIU B. Distillation process simulation analysis based on Hysys[D]. Xi'an: Xidian University, 2013. http://cdmd.cnki.com.cn/article/cdmd-10701-1014330507.htm |
| [53] |
王炳忠.某型空分设备仿真训练系统研究[D].沈阳: 东北大学, 2010. WANG B Z. The research on a certain type of air separation equipment simulation training system[D]. Shenyang: Northeastern University, 2010. http://d.wanfangdata.com.cn/Thesis/J0104903 |
| [54] |
ZHU Y, LEGG S, LAIRD C D. Optimal design of cryogenic air separation columns under uncertainty[J]. Computers & Chemical Engineering, 2010, 34(9): 1377-1384. |
| [55] |
BANSAL V, PERKINS J D, PISTIKOPOULOS E N. A Case study in simultaneous design and control using rigorous, mixed-integer dynamic optimization models[J]. Industrial & Engineering Chemistry Research, 2002, 41(4): 760-778. |
| [56] |
MILLER J, LUYBEN W L, BELANGER P, et al. Improving agility of cryogenic air separation plants[J]. Industrial & Engineering Chemistry Research, 2008, 47(2): 394-404. |
| [57] |
GUO T, LU J, XIANG W, et al. Dynamic modeling and control of the air separation unit in an IGCC power plant[C]//Proceedings of the 2009 International Conference on Sustainable Power Generation and Supply, Piscataway: IEEE, 2009: 1-7.
|
| [58] |
XENOS D P, KAHRS O, CICCIOTTI M, et al. Challenges of the application of data-driven models for the real-time optimization of an industrial air separation plant[C]//Proceedings of the 2016 European Control Conference, Piscataway: IEEE, 2017: 1025-1030.
|
| [59] |
DIEHL M. Real-time optimization for large scale nonlinear processes[M]. Berlin: Springer-Verlag, 2002: 920.
|
| [60] |
DIEHL M, USLU I, FINDEISEN R, et al. Real-time optimization for large scale processes: nonlinear model predictive control of a high purity distillation column[M]. Berlin: Springer-Verlag, 2001: 363-383.
|
| [61] |
CHIEN I L. Simple empirical nonlinear model for temperature-based high-purity distillation columns[J]. AIChE Journal, 1996, 42(9): 2692-2697. DOI:10.1002/aic.690420931 |
| [62] |
BACHNAS A A, TÓTH R, LUDLAGE J H A, et al. A review on data-driven linear parameter-varying modeling approaches: A high-purity distillation column case study[J]. Journal of Process Control, 2014, 24(4): 272-285. DOI:10.1016/j.jprocont.2014.01.015 |
| [63] |
RUGH W J, SHAMMA J S. Research on gain scheduling[J]. Automatica, 2000, 36(10): 1401-1425. DOI:10.1016/S0005-1098(00)00058-3 |
| [64] |
TÓTH R. Modeling and identification of linear parameter-varying systems[M]. Heidelberg: Springer-Verlag, 2010.
|
| [65] |
HUANG K J, ZONG S, QIAN J X. Compartmental models for separation columns[J]. Chinese Journal of Chemical Engineering, 1996, 4(3): 24-33. |
| [66] |
BORCHARDT J, GRUND F, HORN D. Parallelized numerical methods for large systems of differential-algebraic equations in industrial applications[R]. Berlin: WIAS, 1997.
|
| [67] |
BORCHARDT J, GRUND F, HORN D. Parallelized methods for large nonlinear and linear systems in the dynamic simulation of industrial applications[J]. Surveys on Mathematics for Industry, 1999, 8(3): 201-211. |
| [68] |
MAIER R S, RATH W, PETZOLD L R. Parallel solution of large-scale differential-algebraic systems[J]. Concurrency & Computation Practice & Experience, 1995, 7(8): 795-822. |
| [69] |
BIAN S J, HENSON M A, BELANGER P, et al. Nonlinear state estimation and model predictive control of nitrogen purification columns[J]. Industrial & Engineering Chemistry Research, 2005, 44(1): 153-167. |
| [70] |
BIAN S J, HENSON M A. Measurement selection for on-line estimation of nonlinear wave models for high purity distillation columns[J]. Chemical Engineering Science, 2006, 61(10): 3210-3222. DOI:10.1016/j.ces.2005.11.066 |
| [71] |
KIENLE A. Low-order dynamic models for ideal multicomponent distillation processes using nonlinear wave propagation theory[J]. Chemical Engineering Science, 2000, 55(10): 1817-1828. DOI:10.1016/S0009-2509(99)00463-7 |
| [72] |
KHOWINIJ S, HENSON M A, BELANGER P, et al. Dynamic compartmental modeling of nitrogen purification columns[J]. Separation & Purification Technology, 2005, 46(1/2): 95-109. |
| [73] |
CHEN Z, HENSON M A, BELANGER P, et al. Nonlinear model predictive control of high purity distillation columns for cryogenic air separation[J]. IEEE Transactions on Control Systems Technology, 2010, 18(4): 811-821. DOI:10.1109/TCST.2009.2029087 |
| [74] |
BENALLOU A, SEBORG D E, MELLICHAMP D A. Dynamic compartmental models for separation processes[J]. AIChE Journal, 1986, 32(7): 1067-1078. DOI:10.1002/aic.690320703 |
| [75] |
HORTON R R, BEQUETTE B W, EDGAR T F. Improvements in dynamic compartmental modeling for distillation[J]. Computers & Chemical Engineering, 1991, 15(3): 197-201. |
| [76] |
WONG K T, LUUS R. Model reduction of high-order multistage systems by the method of orthogonal collocation[J]. Canadian Journal of Chemical Engineering, 1980, 58(3): 382-388. DOI:10.1002/cjce.5450580315 |
| [77] |
CHO Y S, JOSEPH B. Reduced-order steady-state and dynamic models for separation processes. Part Ⅰ. Development of the model reduction procedure[J]. AIChE Journal, 1983, 29(2): 261-269. DOI:10.1002/aic.690290213 |
| [78] |
李琦, 邵诚. 气体分馏装置精馏过程的动态建模与仿真[J]. 系统仿真学报, 2009, 21(14): 4492-4496. LI Q, SHAO C. Dynamic modeling and simulation of distillation process in gas fractionation equipments[J]. Journal of System Simulation, 2009, 21(14): 4492-4496. |
| [79] |
BIEGLER L T, GROSSMANN I E. Retrospective on optimization[J]. Computers & Chemical Engineering, 2004, 28(8): 1169-1192. |
| [80] |
RODRIGUEZ J. Large-scale dynamic optimization using code generation and parallel computing[D]. Stockholm: Royal Institute of Technology School of Engineering Sciences, 2014.
|
| [81] |
邵之江. 大规模过程系统优化的简约空间SQP算法[J]. 系统工程理论与实践, 1999, 19(1): 56-60. SHAO Z J. Reduced-space SQP algorithm based on orthogonal decomposition for large-scale process optimization[J]. Systems Engineering-theory & Practice, 1999, 19(1): 56-60. DOI:10.3321/j.issn:1000-6788.1999.01.010 |
| [82] |
江爱朋, 邵之江, 陈曦, 等. 基于简约空间序列二次规划算法和混合求导方法的精馏塔操作优化[J]. 化工学报, 2006, 57(6): 1378-1384. JIANG A P, SHAO Z J, CHEN X, et al. Operation optimization of distillation column based on reduced SQP algorithm and hybrid derivative method[J]. Journal of Chemical Industry and Engineering, 2006, 57(6): 1378-1384. DOI:10.3321/j.issn:0438-1157.2006.06.021 |
| [83] |
CUTHRELL J E, BIEGLER L T. On the optimization of differential-algebraic process systems[J]. AIChE Journal, 1987, 33(8): 1257-1270. DOI:10.1002/aic.690330804 |
| [84] |
CERVANTES A, BIEGLER L T. Large-scale DAE optimization using a simultaneous NLP formulation[J]. AIChE Journal, 2010, 44(5): 1038-1050. |
| [85] |
BIEGLER L T, CERVANTES A M, WÄCHTER A. Advances in simultaneous strategies for dynamic process optimization[J]. Chemical Engineering Science, 2002, 57(4): 575-593. DOI:10.1016/S0009-2509(01)00376-1 |
| [86] |
ÇELIK E, BAYRAM M. Solution of differential-algebraic equations (DAEs) by Adomian decomposition method[J]. Pure & Applied Mathematical Sciences, 2006, 3(1): 93-100. |
| [87] |
JIE X, HUANG Y, LOU H H. A probability distribution estimation based method for dynamic optimization[J]. AIChE Journal, 2007, 53(7): 1805-1816. DOI:10.1002/aic.11209 |
| [88] |
张正江, 邵之江, 陈曦, 等. 一种求解数据校正问题的基于经验增强的方法[J]. 高校化学工程学报, 2011, 25(3): 482-488. ZHANG Z J, SHAO Z J, CHEN X, et al. An optimization method based on mnemonic enhancement for solving data reconciliation problems[J]. Journal of Chemical Engineering of Chinese Universities, 2011, 25(3): 482-488. DOI:10.3969/j.issn.1003-9015.2011.03.022 |
| [89] |
李传坤, 赵东风, 王春利, 等. 一种化工过程故障诊断知识自动化方法研究[J]. 高校化学工程学报, 2018, 32(2): 393-400. LI C K, ZHAO D F, WANG C L, et al. Study on a knowledge automation method for fault diagnosis of chemical processes[J]. Journal of Chemical Engineering of Chinese Universities, 2018, 32(2): 393-400. DOI:10.3969/j.issn.1003-9015.2018.02.018 |




