2. 西安交通大学 能源与动力学院,陕西 西安 710049
2. School of Energy and Power Engineering, Xi'an Jiaotong University, Xi'an 710049, China
折流杆换热器(rod-baffle heat exchangers,RBHEs)由美国菲利普石油公司于1970年首次提出并制造,用折流栅代替折流板,有防止管束振动,降低壳程压降,减少流动死区和漏流损失等优点[1-4]。很多学者对传统RBHEs(换热管为圆管且四边形布置,折流杆为圆杆)进行了研究。Philiips公司GENTRY等[5-8]和中国郑州大学热能研究中心、董其伍等[9]和马小明等[10]做了大量实验,得到了传统RBHEs壳程努塞尔数Nu和摩擦系数f的经验关联式。在此基础上,研究集中在改变折流杆结构,换热管结构及其布管方式。实验方面:陈文昕[11]得出了三角形布管RBHEs经验关联式,与现有的正方形布管经验关联式比较,结果表明三角形布管方式更优。严良文等[12-13]研究了波形折流杆、三角形布管的RBHEs,其总传热系数高于折流板换热器。孔松涛等[14]证明了层流时45°菱形折流杆的RBHEs综合传热系数比传统RBHEs高20%。WANG等[15]发现雷诺数Re在2 000 ~ 4 800时,螺纹管RBHEs的传热系数比光管大38%,压降相当。模拟方面:整体模型为主,多孔介质模型、周期性单元流道模型、周期性全截面模型、和“分段模拟,整体综合”为辅。YANG等[16]对比了模拟与实验结果发现了多孔介质模型和整体模型能够同时准确计算传热和压降。刘佳驹等[17-18]对比发现了深槽螺旋波纹管RBHEs综合性能优于光管RBHEs。WANG等[19]证明波形折流杆,三角形布管的RBHEs壳程的综合换热性能比传统RBHEs大10%。YU等[20]提出了六角形夹持和圆弧夹持式RBHEs,结果表明六角形夹持结构的刚度大,适用于大、重管束,传热效果好,但整体性能指标低于圆弧夹持结构。YOU等[21]使用周期单元流道模型,对比发现带凹槽折流杆的RBHEs的交错排列形式的传热系数h比非交错排列形式提高了41.9%,压降增大一倍,传热系数与压降比(h·△P-1)更大。YUAN等[22]证明了RBHEs与折流板换热器的传热相当,但压降大幅度降低。WANG等[23]证明双壳程的h·△P-1比单壳程RBHEs提高了约8.9%。无论实验还是模拟,对RBHEs进行换热管结构改进的文献很少,借鉴现有的纵向流管壳式换热器传热管形式,基于流动传热强化机理,本文提出用螺旋扁管代替圆管安装在RBHEs中。对比了螺旋扁管RBHEs和圆管RBHEs壳程的流动、传热和综合性能。
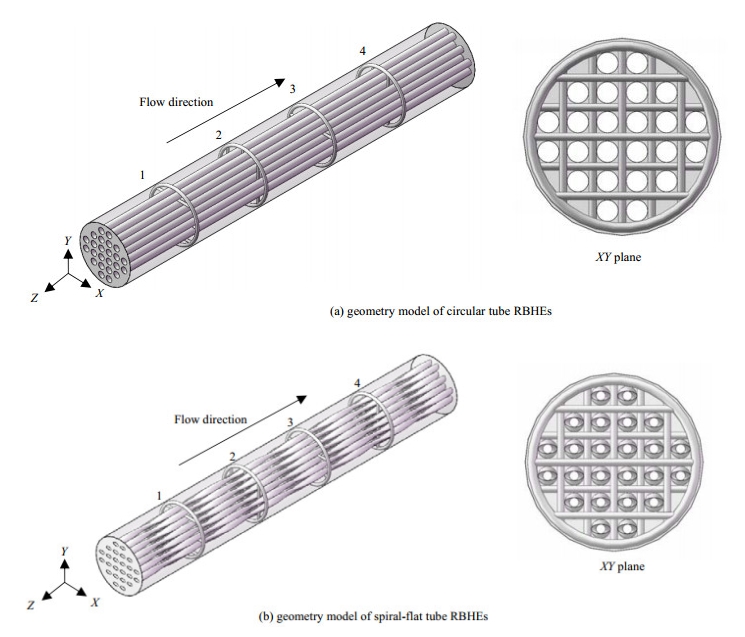
2 折流杆换热器的整体模拟 2.1 几何模型及网格划分按照GB151-2014标准,设计并建立了螺旋扁管RBHEs和圆管RBHEs壳程的几何模型,如图 1所示,坐标原点在入口正中心。2种模型换热管尺寸不一样,其余结构参数都相同。圆管的直径是16 mm。螺旋扁管的横截面是椭圆,长轴为16 mm,短轴为8 mm,螺距为266.7 mm。管间距为22 mm;壳体内径是147 mm;壳体和换热管长度均为1 000 mm。折流栅间距为200 mm,双排管间布管,沿着流动方向被定义为第1、2、3和4个折流栅,由折流环和折流杆组成。折流环的横截面为圆形,直径为7.3 mm;折流杆的直径为6 mm。螺旋扁管的长轴等于圆管直径,便于将圆管抽出后,螺旋扁管直接插入安装。
|
图 1 折流杆换热器的几何模型 Fig.1 Geometry model of RBHEs |
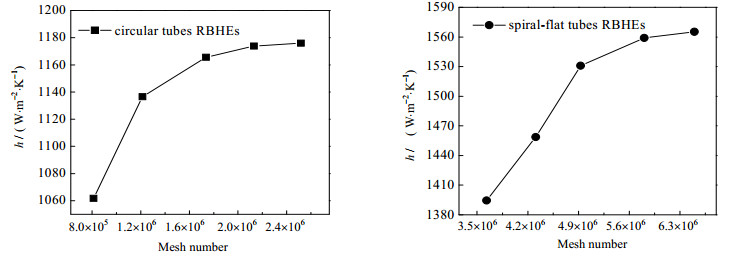
先使用ANSYS Meshing对几何模型进行了非结构化网格划分,导入Fluent中转化为多面体网格,大大降低网格数量并提高网格质量。对圆管RBHEs和螺旋扁管RBHEs分别进行了网格独立性验证,结果如图 2所示。圆管RBHEs模型在网格数量达到1 213 899后,换热系数h变化低于2.56%,螺旋扁管RBHEs模型在网格数量高于4 928 456时,换热系数h和变化小于1.84%。圆管和螺旋扁管RBHEs最终取定的网格数量分别为1 737 729和5 383 816。
|
图 2 网格独立性验证 Fig.2 Validation of mesh independence |
壳程工作流体为水,假设为不可压缩流体湍流流动,忽略重力和水物性的变化。入口速度边界条件,为0.1、0.2、0.3、0.4、0.5和0.6 m·s-1,水的进口温度为300 K。压力出口边界条件。管内为低温沸点工质冷凝,设定管壁温度为350 K。其余壁面均为无滑移绝热壁面。采用标准k-ε湍流模型和标准的壁面函数模型。压力和速度耦合采用SIMPLE算法,动量和能量方程均采用二阶迎风格式,湍动能和湍流耗散率方程均采用一阶迎风格式。残差值除能量方程需小于1×10-6,其余项小于1×10-3认为收敛。标准k-ε模型的控制方程如下:
连续性方程:
| $ \frac{\partial }{{\partial {x_j}}}({u_j}) = 0 $ | (1) |
动量方程:
| $ \frac{\partial }{{\partial {x_j}}}(\rho {u_j}{u_i}) = \frac{\partial }{{\partial {x_j}}}\left( {{\eta _{{\rm{eff}}}}\frac{{\partial {u_i}}}{{\partial {x_j}}}} \right) - \frac{{\partial P}}{{\partial {x_i}}} $ | (2) |
能量方程:
| $ \frac{\partial }{{\partial {x_j}}}(\rho {u_j}T) = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\frac{\eta }{{Pr}}{\rm{ + }}\frac{{{\eta _{{\rm{tur}}}}}}{{{\sigma _t}}}} \right)\frac{{\partial T}}{{\partial {x_j}}}} \right]{\rm{ + }}{S_T} $ | (3) |
湍动能k方程:
| $ \frac{\partial }{{\partial {x_j}}}\left( {\rho k{u_j}} \right) = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\eta {\rm{ + }}\frac{{{\eta _{{\rm{tur}}}}}}{{{\sigma _k}}}} \right)\frac{{\partial k}}{{\partial {x_j}}}} \right] + {G_k} + \rho \varepsilon $ | (4) |
湍动能耗散ε方程:
| $ \frac{\partial }{{\partial {x_j}}}\left( {\rho \varepsilon {u_j}} \right) = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\eta + \frac{{{\eta _{{\rm{tur}}}}}}{{{\sigma _\varepsilon }}}} \right)\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right] + \frac{\varepsilon }{k}\left( {{G_k}{C_{{\rm{1}}\varepsilon }} - {C_{{\rm{2}}\varepsilon }}\rho \varepsilon } \right) $ | (5) |
式中:
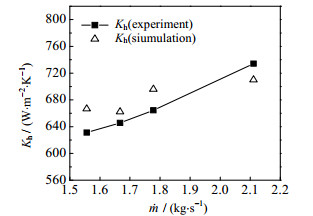
将折流杆换热器壳程和管程同时模拟,与文献[24]壳程为冷水,管程为热水,折流栅间距为120 mm的工况所得实验数据进行对比。管程和壳程入口边界条件为质量流量和温度,其余设置与上述相同。模拟和实验所得到换热器总换热系数Kh的偏差如图 3所示。Kh的最大偏差为5.63%,平均偏差为4.06%。偏差的主要原因有模型的简化;除换热管的其余壁面绝热、水物性不变的假设;忽略重力的影响等。
|
图 3 实验与模拟结果对比 Fig.3 Comparison of experimental and simulation results |
图 4和图 5分别为入口速度0.1和0.6 m·s-1时,折流杆换热器X=0,YZ平面速度云图。取速度范围的最小值和最大值速度云图分析,可以分析低速入口条件和高速入口条件对流场的影响。
|
图 4 入口速度vinlet为0.1 m·s-1的速度云图 Fig.4 Velocity contour at inlet velocity vinlet of 0.1 m·s-1 |
|
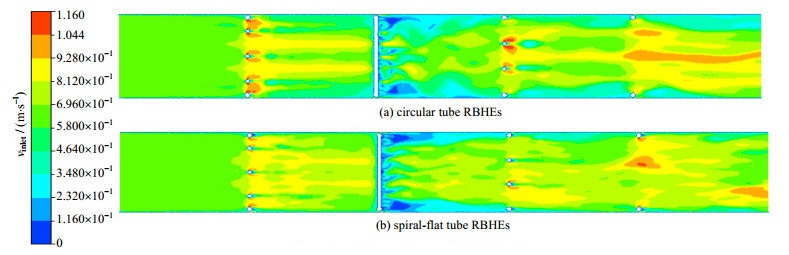
图 5 入口速度vinlet为0.6 m·s-1的速度云图 Fig.5 Velocity contour at inlet velocity vinlet of 0.6 m·s-1 |
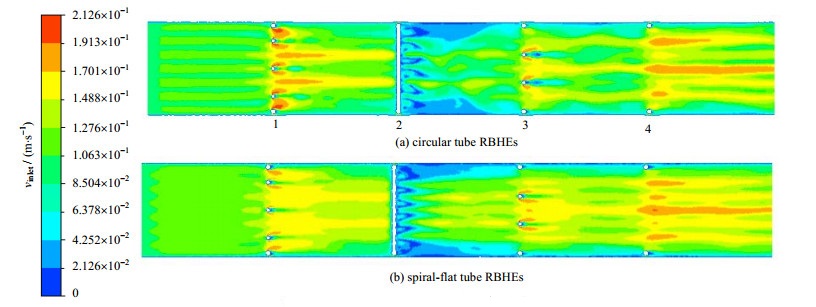
从图 4和5中可以看出,圆管RBHEs中的高速区和低速区相对较多,速度大小差别更大,速度分布更加不均匀。在高速入口条件下,2种模型壳程流速不均匀度的差别缩小。从流经每个折流栅后的流场可以看出,圆管RBHEs中折流栅对流体的作用更大。图中流经第1、3和4折流栅时,由于流通截面积的减小,流速会增大,在圆管RBHEs中流速增大更明显。在流经第2个折流栅时,因为所截平面刚好穿过第2个折流栅中间折流杆的中心线,受到折流杆的阻拦,速度降低并波动,在圆管RBHEs中这种波动更明显。
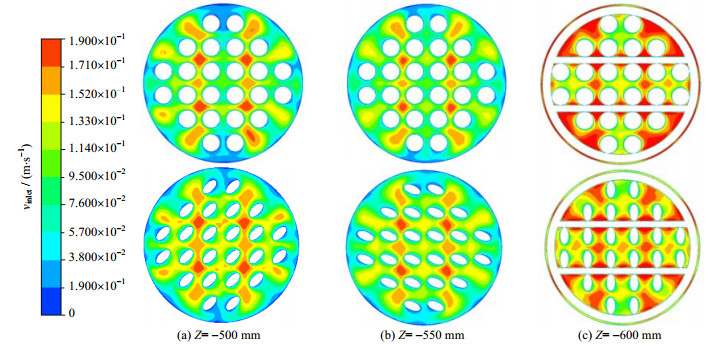
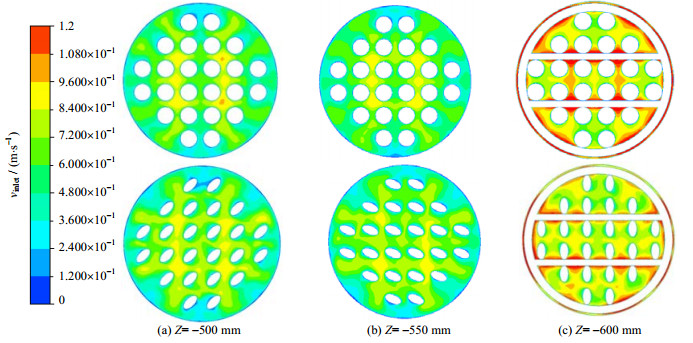
图 6和7是入口速度为0.1、0.6 m·s-1时,2种折流杆换热器Z= -500、-550和-600 mm,XY平面速度云图。从Z= -500和-550 mm云图中可以看出,螺旋扁管RBHEs的管间流速更大,速度分布更加均匀。由Z= -600 mm的云图可以看出,圆管RBHEs流经折流栅时的速度更大。从图 6和7中比较可以看出,高入口速度条件下,2种RBHEs速度不均匀度的差距在减小。
|
图 6 入口速度vinlet为0.1 m·s-1的速度云图 Fig.6 Velocity contour at inlet velocity vinlet of 0.1 m·s-1 |
|
图 7 入口速度vinlet为0.6 m·s-1的速度云图 Fig.7 Velocity contour at inlet velocity vinlet of 0.6 m·s-1 |
综上,螺旋扁管RBHEs的管间速度更大,分布更加均匀,因为螺旋扁管的扭转曲面,周期性扰动流体,改变流体的流速和流向,加强了流体的纵向混合。流经折流栅部分,圆管RBHEs的流速更大,速度波动也更大,有3方面的原因:1是折流栅结构相同,圆管入口流通面积小于螺旋扁管RBHEs,折流栅的存在使得流通面积减小相同,但圆管RBHEs的减小率更大。2是圆管RBHEs换热管与折流杆的垂直相切处的流通缝隙更小。3是圆管RBHEs的圆管对流体的扰动没有螺旋扁管强,流体流经折流栅引起的速度波动更明显。
图 8和图 9是入口速度为0.1、0.6 m·s-1时,2种折流杆换热器Z= -500 mm,XY平面湍动能云图。由图可见,螺旋扁管RBHEs换热管椭圆截面两端湍动能很高;圆管RBHEs的湍动能均匀度更好。螺旋扁管RBHEs湍动能大的区域(绿色和红色部分)更加多而且分散,在换热管贴壁处和管间均有分布。因为螺旋扁管扰动流体,形成了复杂的周期性流动和混合,湍动能增大。而圆管RBHEs在入口速度为0.1 m·s-1时,湍动能大的区域仅分布在换热管周围,在入口速度为0.6 m·s-1时,在壳体贴壁处也存在,而且贴壁处的湍动能增强。随着入口速度的增大,两种换热器湍动能均匀度的差别在缩小。

|
图 8 入口速度vinlet为0.1 m·s-1的湍动能 Fig.8 Turbulence kinetic energy contour at inlet velocity vinlet of 0.1 m·s-1 |

|
图 9 入口速度vinlet为0.6 m·s-1的湍动能 Fig.9 Turbulence kinetic energy contour at inlet velocity vinlet of 0.6 m·s-1 |
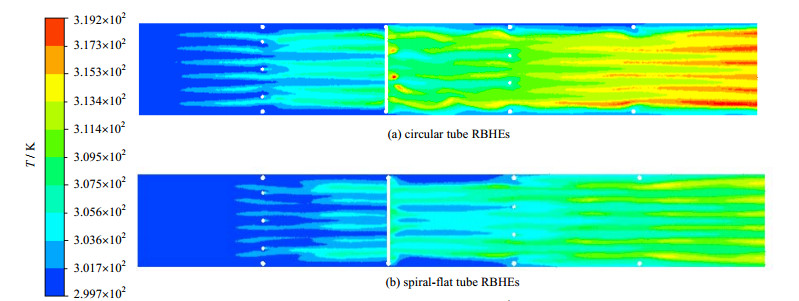
图 10~13是换热器轴线平面(X=0,YZ平面)和径向平面(Z= -500 mm,XY平面)的温度云图。从图 10和11中可以看出,流体在螺旋扁管RBHEs中的温度低于圆管RBHEs,因为在螺旋扁管RBHEs中的流体速度整体高于圆管,另外在圆管折流杆换热器中的RBHEs更大,分布更不均匀,这与流场的不均匀度大有关。
|
图 10 入口速度vinlet为0.1 m·s-1的温度云图 Fig.10 Temperature contour at inlet velocity vinlet of 0.1 m·s-1 |
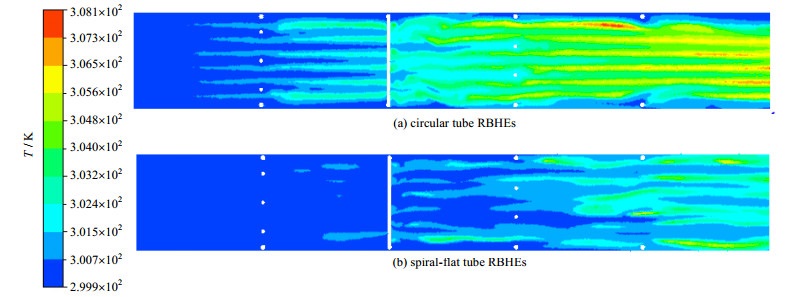
|
图 11 入口速度vinlet为0.6 m·s-1的温度云图 Fig.11 Temperature contour at inlet velocity vinlet of 0.6 m·s-1 |
从图 12和13可以看出,圆管RBHEs中管间的温度高于螺旋扁管RBHEs,同样是管间流体速度低所致。圆管换热器管间温度高的现象在0.6 m·s-1中的现象被减弱,因为在高速入口条件下,圆管RBHEs的管间速度得到增强,螺旋扁管增强管间速度的作用被减弱。螺旋扁管RBHEs的贴近换热管处的温度明显高于相同入口速度条件下圆管RBHEs,因为螺旋扁管附近的湍动能大于圆管附近,能够增强换热,该处流体温度得到提高。
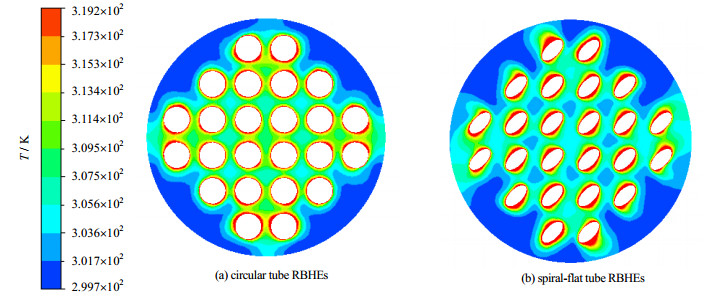
|
图 12 入口速度vinlet为0.1 m·s-1的温度云图 Fig.12 Temperature contour at inlet velocity vinlet of 0.1 m·s-1 |
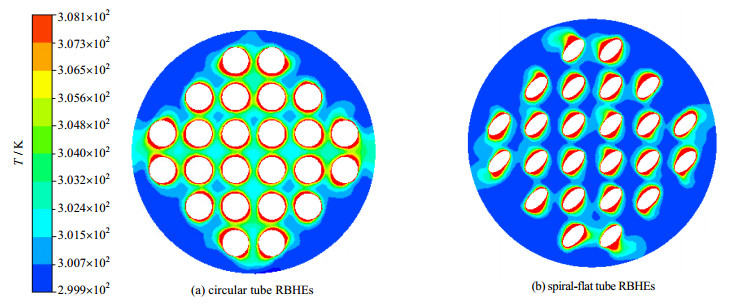
|
图 13 入口速度vinlet为0.6 m·s-1的温度云图 Fig.13 Temperature contour at inlet velocity vinlet of 0.6 m·s-1 |
图 14为圆管和螺旋扁管RBHEs壳程换热系数h随入口速度变化曲线图。由图可以看出,在低速入口条件下,螺旋扁管RBHEs的壳程传热系数h高于圆管RBHEs,在高速入口条件下,螺旋扁管RBHEs的h低于圆管。在入口速度0.1 m·s-1的条件下,螺旋扁管RBHEs的传热系数h比圆管折流杆换热器大42.29%,在入口速度为0.6 m·s-1的条件下,比圆管RBHEs小6.63%。因为螺旋扁管RBHEs的换热管对流体形成扰动强于圆管RBHEs,而折流栅部分对流体的扰动弱于圆管RBHEs,低入口速度条件下,加强换热方面更强,高入口速度条件下,削弱换热方面更强。可见螺旋扁管增强流体扰动来增强换热的机理更适合用于流体速度较低时,在流体速度较高时,流体主流区流量增大,螺旋结构影响变小。这与文献[25]研究的单管螺旋扁管代替圆管增强换热的方法更适用于低Re下流动的结论一致。
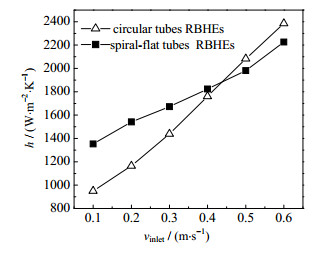
|
图 14 传热系数h随入口速度vinlet的变化 Fig.14 Profiles of heat transfer coefficient h as a function of inlet velocity vinlet |
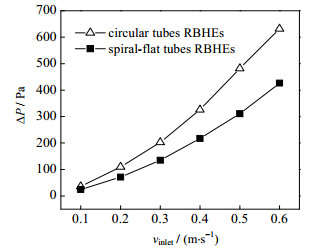
不同入口速度条件下RBHEs壳程压降△P的变化图如图 15所示,由图可知,在相同入口速度条件下,螺旋扁管RBHEs的压降低于圆管RBHEs,减少了约33.60 %。因为折流杆换热器的压降主要由无折流栅时的压降和单独由折流栅引起的压降两部分组成,在螺旋扁管RBHEs中,由折流栅部分引起的压降远低于圆管RBHEs。因为圆管RBHEs中,流经折流栅,流速变化大,后续波动更明显,所造成的流动损失更大。
|
图 15 压降△P随入口速度vinlet的变化 Fig.15 Profiles of pressure drop △P as a function of inlet velocity vinlet |
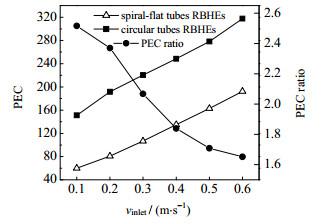
图 16为螺旋扁管RBHEs和圆管RBHEs综合性能评价指标(performance evaluation criteria,PEC)和两者的比值随不同入口速度的变化。PEC为Nu·f-1/3,Nu、f分别为换热器壳程的努塞尔数、摩擦系数,是换热器综合性能的评价指标。从图中可以看出,螺旋扁管RBHEs的综合性能优于圆管RBHEs。随着速度的增大,螺旋扁管与圆管RBHEs的PEC比值从2.52降低到1.65。在0.1 m·s-1的入口速度时,螺旋扁管RBHEs的综合性能比圆管RBHEs提高152%,在入口速度为0.6 m·s-1时,提高了65%。因为螺旋扁管RBHEs在不同入口速度条件下,虽然不一定能够增大换热系数,但其压降总是低于圆管RBHEs,综合性能更优。
|
图 16 综合性能评价指标PEC及其比值随入口速度vinlet的变化 Fig.16 Profiles of comprehensive performance efficiency criteria PEC and PEC ratio as a function of inlet velocity vinlet |
本文提出将传统圆管折流杆换热器(rod-baffle heat exchangers,RBHEs)中的换热管改成螺旋扁管以达到强化传热的目的,建立了圆管RBHEs和螺旋扁管RBHEs的几何模型,用数值模拟的方法,比较了两者流动、传热和综合性能。得出以下结论:
(1) 螺旋扁管RBHEs的螺旋结构能够改变流体的流速和流向,增强纵向混合,增大管间流体速度,使速度大小分布更加均匀,在高速入口条件下,增强效果被减弱。换热管的附近,螺旋扁管RBHEs流体湍动能更大,温度更高。
(2) 在相同低速入口条件下,螺旋扁管RBHEs的传热系数h高于圆管折流杆换热器,在相同的高速入口条件下,螺旋扁管RBHEs的h小于圆管折流杆换热器,两者存在交叉点。
(3) 在相同的入口速度条件下,螺旋扁管折流杆换热器的压降△P比圆管折流杆换热器的降低了约33.60%。
(4) 在入口速度为0.1~0.6 m·s-1,螺旋扁管RBHEs的综合性能评价指标PEC(performance evaluation criteria)比圆管RBHEs高65%~152%。低入口速度条件下,螺旋扁管RBHEs的综合性能优势更明显。
符号说明:
|
|
| [1] |
徐烨琨, 刘成, 李永辉. 折流杆换热器的研究方法进展[J]. 化工进展, 2014, 33(7): 1671-1676. XU Y K, LIU C, LI Y H. Progress of rod baffle heat exchanger[J]. Chemical Industry and Engineering Progress, 2014, 33(7): 1671-1676. |
| [2] |
李炜炜.管壳式换热器壳程强化传热研究[D].武汉: 华中科技大学, 2007. LI W W. Study on heat transfer enhancement in shell side of shell and tube heat exchangers[D]. Wuhan: Huazhong University of Science and Technology, 2007. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=xdhg200107004 |
| [3] |
吴金星, 董其伍, 刘敏珊, 等. 折流杆换热器壳程湍流和传热的数值模拟[J]. 高校化学工程学报, 2006, 20(2): 213-216. WU J X, DONG Q W, LIU M S, et al. Numerical simulation on the turbulent flow and heat transfer in the shell side of the rod baffle heat exchanger[J]. Journal of Chemical Engineering of Chinese Universities, 2006, 20(2): 213-216. DOI:10.3321/j.issn:1003-9015.2006.02.011 |
| [4] |
吴金星, 魏新利, 董其伍, 等. 花瓣孔板纵流式换热器的研发及试验研究[J]. 高校化学工程学报, 2008, 22(2): 205-209. WU J X, WEI X L, DONG Q W, et al. Experimental investigation and development of the petal orifice-baffle longitudinal flow type heat exchangers[J]. Journal of Chemical Engineering of Chinese Universities, 2008, 22(2): 205-209. DOI:10.3321/j.issn:1003-9015.2008.02.005 |
| [5] |
GENTRY C C, YOUNG R K, SMALL W M. Rodbaffle heat exchanger thermal-hydraulic predictive methods for bare and low-finned tubes[C]//Proc. 22nd Natl. Heat Transfer Conf., Niagara: 1984: 104-109.
|
| [6] |
GENTRY C C, YOUNG R K, SMALL W M. Rodbaffle heat exchanger-thermal-hydraulic predictive methods[C]//Proc. 23rd Natl. Heat Transfer Conf., Munich: 1982: 197-202.
|
| [7] |
GENTRY C C, SMALL W M. Rodbaffle exchanger-thermal-hydraulic predictive models over expanded baffle-spacing and Reynolds number ranges[C]//Proc. 23rd Natl. Heat Transfer Conf., Denver: 1985: 103-108.
|
| [8] |
GENTRY C C. Rodbaffle heat exchanger technology[J]. CEP, 1990, 86(7): 48-57. |
| [9] |
董其伍, 刘敏珊. 纵流壳程换热器[M]. 北京: 化学工业出版社, 2006. DONG Q W, LIU M S. Heat exchangers with longitudinal flow of shell-side[M]. Beijing: Chemical Industry Press, 2006. |
| [10] |
马小明, 钱颂文, 朱冬生, 等. 管壳式换热器[M]. 北京: 中国石化出版社, 2010: 105-114. MA X M, QIAN S W, ZHU D S, et al. Shell and tube heat exchangers[M]. Beijing: China Petrochemical Press, 2010: 105-114. |
| [11] |
陈文昕.折流杆换流器的数值模拟与实验研究[D].广州: 华南理工大学, 2006. CHEN W X. Numerical simulation and experimental research of rod baffle heat exchangers[D]. Guangzhou: South China University of Technology, 2006. |
| [12] |
YAN L W, WU J X, WANG Z W. Industrially experimental investigations and development of the curve-rod baffle heat exchanger[J]. Journal of Shanghai University:English Edition, 2004, 8(3): 337-341. DOI:10.1007/s11741-004-0075-6 |
| [13] |
严良文, 王志文. 波形折流杆换热器的工业实验研究[J]. 华东理工大学学报, 2004, 3(8): 478-480. YAN L W, WANG Z W. Industrial investigation of heat exchanger with curve-rod baffle[J]. Journal of East China University of Science and Technology, 2004, 3(8): 478-480. |
| [14] |
孔松涛, 董其伍, 刘敏珊. 菱形折流杆换热器传热研究[J]. 石油机械, 2007, 35(1): 683-686. KONG S T, DONG Q W, LIU M S. Study of heat transfer in diamond rodbaffle heat exchanger[J]. China Petroleum Machinery, 2007, 35(1): 683-686. |
| [15] |
WANG X S, WANG R Z, WU J Y. Experimental investigation of a new-style double-tube heat exchanger for heating crude oil using solar hot water[J]. Applied Thermal Engineering, 2005, 25(11/12): 1753-1763. |
| [16] |
YANG J, MA L, BOCK J, et al. A comparison of four numerical modeling approaches for enhanced shell-and-tube heat exchangers with experimental validation[J]. Applied Thermal Engineering, 2014, 65(1/2): 369-383. |
| [17] |
刘佳驹.螺旋异型管强化传热数值研究及PIV实验分析[D].武汉: 华中科技大学, 2015 LIU J J. Numerical research and PIV experimental analysis on heat transfer enhancement of helical shaped tubes[D]. Wuhan: Huazhong University of Science and Technology, 2015 |
| [18] |
LIU J J, LIU Z C, LIU W. 3D numerical study on shell side heat transfer and flow characteristics of rod-baffle heat exchangers with spirally corrugated tubes[J]. International Journal of Thermal Sciences, 2015, 89: 34-42. DOI:10.1016/j.ijthermalsci.2014.10.011 |
| [19] |
WANG X T, ZHENG N B, LIU P, et al. Analysis of flow and heat transfer capability in rod baffle heat exchangers with ripple rods[J]. Journal of Engineering Thermophysics, 2016, 37(8): 1758-1762. |
| [20] |
YU C L, REN Z W, ZENG M. Numerical investigation of shell-side performance for shell and tube heat exchangers with two different clamping type anti-vibration baffles[J]. Applied Thermal Engineering, 2018, 133: 125-136. DOI:10.1016/j.applthermaleng.2018.01.029 |
| [21] |
YOU Y H, ZHANG F H, FAN A W, et al. A numerical study on the turbulent heat transfer enhancement of rodbaffle heat exchanger with staggered tubes supported by round rods with arc cuts[J]. Applied Thermal Engineering, 2015, 76: 220-232. DOI:10.1016/j.applthermaleng.2014.11.048 |
| [22] |
YUAN Z C, LIU J Z, YAN H S. Performance comparison of rod-baffle and segment-baffle heat exchangers using numerical simulations[J]. Applied Mechanics and Materials, 2014, 595: 128-133. DOI:10.4028/www.scientific.net/AMM.595.128 |
| [23] |
WANG X T, ZHENG N B, LIU P, et al. Numerical investigation of shell side performance of a double shell side rod baffle heat exchanger[J]. International Journal of Heat and Mass Transfer, 2017, 108(B): 2029-2039. |
| [24] |
邢华伟.新型换热设备——折流杆换热器性能研究[D].武汉: 华中科技大学, 1996. XING H W. New-type heat transfer equipment-research on performance of rob baffle heat exchangers[D]. Wuhan: Huazhong University of Science and Technology, 1996. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y216418 |
| [25] |
思勤, 夏清, 梁龙虎, 等. 螺旋扁管换热器传热与阻力性能[J]. 化工学报, 1995, 46(5): 601-607. SI Q, XIA Q, LIANG L H, et al. Heat transfer and resistance performance of spiral-flat tube heat exchangers[J]. Journal of Chemical Industry and Engineering (China), 1995, 46(5): 601-607. |




