2. 陕西省洁净煤转化工程技术中心,陕西 西安 710069;
3. 西安交通大学 能源与动力工程学院,陕西 西安 710049
2. Shan xi Research Center of Engineering Technology for Clean Coal Conversion, Xi'an 710069, China;
3. School of Energy and Power Engineering, Xi'an Jiao tong University, Xi'an 710049, China
喷动床技术在造粒、制药、煤气化、燃烧、热解、烟气脱硫及催化聚合等工业过程中存在着广泛应用[1-7]。由于传统柱锥型喷动床内介质颗粒具有明显的内外分层流动特点,床层内的气体与颗粒缺少横向混合,特别是在环隙区底部出现颗粒堆积与流动死区,和某些颗粒易黏结的团聚现象,对床体结构的传热传质产生不利的影响。为了克服以上不利影响,新一代喷动-流化床兼具有喷动床与流化床的优点,而得到了喷动床研究者与流化床研究者的共同重视及发展[6-7],文献[8]提出了一种整体式多喷嘴喷动-流化床结构(如图 1所示),在不需要旁路供气辅助设备情况下,能有效消除喷动床内锥体流动死区,从而强化喷动床内气固两相间的传热传质过程。
|
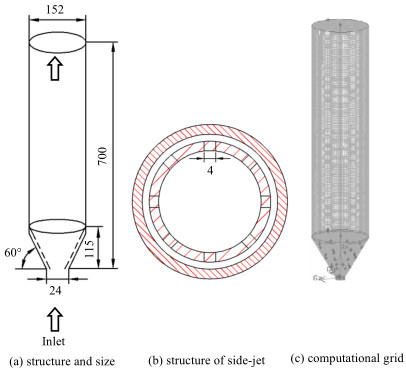
图 1 多喷嘴喷动–流化床结构示意图及网格划分 Fig.1 Geometry and grids of the multi-jet spout-fluidized bed (unit: mm) |
对二维整体式多喷嘴喷动-流化床内的气固两相流动规律进行数值模拟分析。由于二维模型不能真实体现侧喷嘴丰富的空间结构参数(尺寸、形状)与分布特征(数量、布型)对气固两相流动的影响。因此,很有必要将二维模型拓展到三维模型,在三维数值模拟的基础上更加真实地研究分析整体式多喷嘴喷动-流化床内气固两相流动特性。随着计算机技术和流体力学学科的快速发展,数值模拟分析已逐渐成为研究喷动床内颗粒运动、传质传热特性的主要手段,其分析方法已被广泛地应用于多相流态化的过程研究[9-17]。其中TAKABATAKE等[17]采用能粗颗粒模型实现了喷动床内的颗粒混合效果模拟,并分析了固体混合与固体颗粒的宏观行为之间的相关性。本文基于文献[18-19]的实验文献的数值模型,采用Fluent15.0软件对三维整体式多喷嘴喷动-流化床内气固两相流动规律进行了数值模拟,将模拟结果与常规喷动床进行了对比分析,特别是环隙区底部(圆锥处)的气固两相流动特性,并对侧喷嘴设计参数(侧壁开孔直径)进行了优化,从而为整体式多喷嘴喷动-流化床的工程设计提供理论依据。
2 数学模型 2.1 质量守恒方程连续性方程
| $ \frac{\partial }{{\partial t}}\left( {{\alpha _{\rm{i}}}{\rho _{\rm{i}}}} \right) + \nabla \cdot \left( {{\alpha _{\rm{i}}}{\rho _{\rm{i}}}{\mathit{\boldsymbol{\nu }}_{\rm{i}}}} \right) = 0 $ | (1) |
其中,i表示气体或颗粒相,α为气体或颗粒体积分数,v为气体或颗粒速度矢量,ρ为气体或颗粒的密度。
2.2 动量守恒方程气体动量守恒方程[6]可表示为
| $ \frac{\partial }{{\partial t}}\left( {{\alpha _{\rm{g}}}{\rho _{\rm{g}}}{\mathit{\boldsymbol{\nu }}_{\rm{g}}}} \right) + \nabla \cdot \left( {{\alpha _{\rm{g}}}{\rho _{\rm{g}}}{\mathit{\boldsymbol{\nu }}_{\rm{g}}}{\mathit{\boldsymbol{\nu }}_{\rm{g}}}} \right) = - {\alpha _{\rm{g}}}\nabla {p_{\rm{g}}} + {\alpha _{\rm{g}}}{\rho _{\rm{g}}}g + {K_{{\rm{gs}}}}\left( {{\mathit{\boldsymbol{\nu }}_{\rm{s}}} - {\mathit{\boldsymbol{\nu }}_{\rm{g}}}} \right) + \nabla \cdot {\mathit{\boldsymbol{\tau }}_{\rm{g}}} $ | (2) |
其中,
颗粒相动量守恒方程:
| $\frac{\partial }{{\partial t}}\left( {{\alpha _{\rm{s}}}{\rho _{\rm{s}}}{\mathit{\boldsymbol{\nu }}_{\rm{s}}}} \right) + \nabla \cdot \left( {{\alpha _{\rm{s}}}{\rho _{\rm{s}}}{\mathit{\boldsymbol{\nu }}_{\rm{s}}}{\mathit{\boldsymbol{\nu }}_{\rm{s}}}} \right) = - {\alpha _{\rm{s}}}\nabla {P_{\rm{s}}} + {\alpha _{\rm{s}}}{\rho _{\rm{s}}}g + {K_{{\rm{gs}}}}\left( {{\mathit{\boldsymbol{\nu }}_{\rm{g}}} - {\mathit{\boldsymbol{\nu }}_{\rm{s}}}} \right) + \nabla \cdot {\mathit{\boldsymbol{\tau }}_{\rm{s}}}$ | (3) |
其中,
Gidaspow曳力模型[7]相间动量交换系数Kgs在浓相中使用Ergun方程计算,在稀相中则使用Wen & Yu方程计算,其计算方法如下:
当
| ${K_{{\rm{Ergun}}}} = 150\frac{{\alpha _{_{\rm{S}}}^2{\mu _{\rm{g}}}}}{{{\alpha _{\rm{g}}}{d^2}}} + 1.75\frac{{{\rho _{\rm{g}}}{\alpha _{\rm{s}}}}}{d}\left| {{\mathit{\boldsymbol{\nu }}_{\rm{g}}} - {\mathit{\boldsymbol{\nu }}_{\rm{s}}}} \right|$ | (4) |
当
| ${K_{{\rm{Wen - Yu}}}} = \frac{{3{C_{\rm{D}}}{\alpha _{\rm{g}}}{\alpha _{\rm{s}}}{\rho _{\rm{g}}}\left| {{\mathit{\boldsymbol{\nu }}_{\rm{g}}} - {\mathit{\boldsymbol{\nu }}_{\rm{s}}}} \right|}}{{4{d_{\rm{p}}}}}\alpha _{\rm{g}}^{ - 2.65}$ | (5) |
其中,
| ${\operatorname{C} _\rm{D}} = \frac{{24}}{{{\alpha _\rm{g}}{{Re }_\rm{s}}}}\left( {1 + 0.15{{Re}_\rm{s}}^{0.687}} \right),{Re_\rm{s}} \leqslant 1000$ | (6) |
| ${C_{\rm{D}}} = 0.44{,_{}}R{e_{\rm{s}}}1000$ | (7) |
为了避免Ergun方程与Wen & Yu方程过渡的不连续性,Gidaspow引进了一个选择函数使两个方程平滑而快速过渡。
| ${\varphi _{{\rm{gs}}}} = \frac{{{{\arctan }_{}}\left[ {150 \times 1.75\left( {0.2 - {\alpha _{\rm{s}}}} \right)} \right]}}{{\rm{ \mathsf{ π} }}} + 0.5$ | (8) |
则气固相间动量交换系数Kgs为
| ${K_{{\rm{gs}}}} = {\varphi _{{\rm{gs}}}}{K_{{\rm{Wen - Yu}}}} + \left( {1 - {\varphi _{{\rm{gs}}}}} \right){K_{{\rm{Ergun}}}}$ | (9) |
|
|
表 1 数值模拟边界条件设定 Table 1 Boundary conditions of numerical simulation |
本文所模拟的多喷嘴喷动-流化床(multi-jet spout- fluidized bed)的基本几何尺寸与文献[18-19]中喷动床相同,三维整体式多喷嘴喷动-流化床设计尺寸及网格划分情况如图 1所示,模拟设置参数如表 2所示。喷动床圆锥处侧壁开孔数量设定为24 (共8排,每排3个),呈现为三维空间均匀分布(图 1(b)),所开圆孔直径范围为δ=1~5 mm。采用双流体模型对三维整体式多喷嘴喷动-流化床内气固两相流动规律进行模拟分析,由于本文所研究的整体式多喷嘴喷动-流化床暂无实验数据用于对比,故采用文献[20]中已验证的数值模型对并将模拟结果与相应尺寸的常规喷动床进行对比。对三维整体式多喷嘴喷动-流化床模拟进行网格无关性分析,计算网格数分别设定为220 643、253 283、286 036、306 790、338 446。
|
|
表 2 两种喷动床数值模拟参数值设定 Table 2 Experimental and simulation parameters of the two spouted beds |
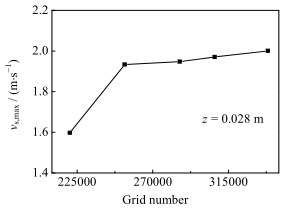
图 2为z = 0.028 m时,不同网格数量所对应的轴中心颗粒最大速度(vs, max)变化规律。计算结果表明,当网格数大于253 283时,数值模拟基本达到了网格无关性的要求,故数值模拟中常规喷动床及多喷嘴喷动流化床的计算网格数分布为234 214和286 036。
|
图 2 网格无关性 Fig.2 Profile of grid independence |
由于流体流动具有连续性,主喷嘴与侧喷嘴的气体流量分配可用侧喷嘴圆孔总横截面积与主喷嘴圆孔面积之比Ai/Az表示(A为喷嘴通道横截面积)。
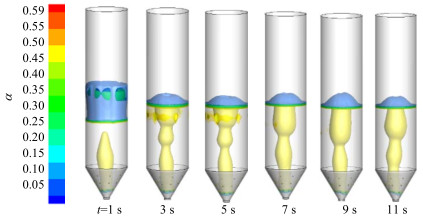
图 3为主喷嘴的入口气体速度为U =1.6Ums,Ai/Az= 0.67 (侧喷嘴直径为4 mm,主喷嘴直径为24 mm)时,多喷嘴喷动-流化床内颗粒体积分数云图随时间的变化规律。由图 3可知,在喷动形成之前喷射区存在不连续的喷动现象,当计算时间大于t=9 s时,三维多喷嘴喷动-流化床内气固两相流体流动结构达到稳定的喷动状态,形成明显的喷射区、喷泉区、环隙区三区结构。故本文采用三维喷动-流化床在计算时间t=9 s时的模拟数据作为研究对象。
|
图 3 多喷嘴喷动–流化床内颗粒体积分数随时间分布情况(U = 1.6Ums) Fig.3 Instantaneous solid volume fraction in the multi-jet spout-fluidized bed |
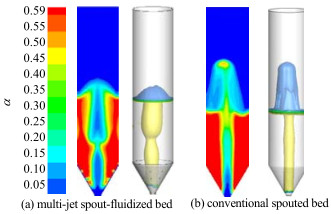
图 4为达到稳定喷动条件下,三维多喷嘴喷动-流化床与常规喷动床的颗粒体积分数云图对比。由图可以看出,三维多喷嘴喷动-流化床的侧壁开孔在一定程度上消除了锥体区的颗粒堆积现象,进口气体的分流作用增强了环隙区颗粒与喷射区气体之间的径向混合与流化作用。此外,在相同的进口气体流量条件下,由于多喷嘴喷动-流化床结构增强了气固混合程度,增加了能量耗散,从而增大了床层总压降,降低了喷泉高度。
|
图 4 两种喷动床稳定喷动时颗粒体积分数分布对比(U = 1.6Ums, t = 9 s) Fig.4 Comparison of contour plots of solid volume fraction in the two spouted beds |
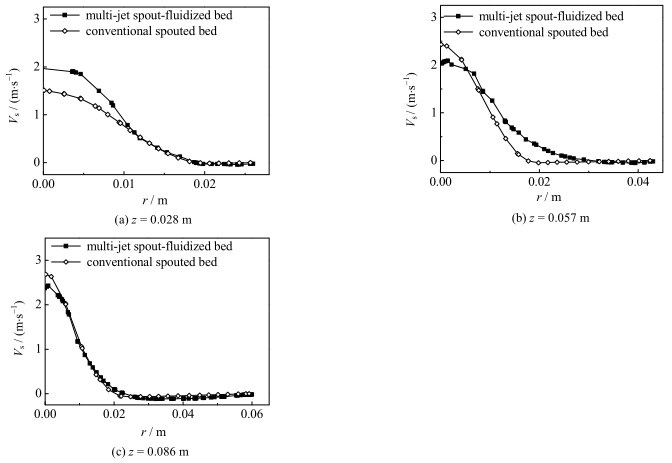
图 5为两种喷动床在不同的床层高度下颗粒速度的径向分布曲线。由图可知,在低床层高度条件下(z=0.028 m),多喷嘴喷动-流化床的颗粒速度高于常规喷动床,表明柱锥区的侧喷嘴进气流量带动了环隙区颗粒的局部流化及运动,使得喷射区与环隙区整体的颗粒速度有所增加。
|
图 5 同床层高度下两种喷动床内颗粒速度径向分布对比 Fig.5 Comparison of particle velocity along radial direction at different bed heights in the two spouted beds |
喷射区与环隙区颗粒速度的增加量随着径向距离的增大而有所降低。随着床层高度的增加,相对于常规喷动床,多喷嘴喷动-流化床的颗粒速度增加程度逐渐降低,当床层高度增加了一定程度时(z=0.086 m),喷动-流化床喷射区颗粒速度反而低于常规喷动床,表明多喷嘴喷动-流化床对颗粒运动的强化作用主要体现在柱锥区与环隙区,这对于提高喷动床内颗粒、气体的充分接触与颗粒群的均匀分布具有积极作用。
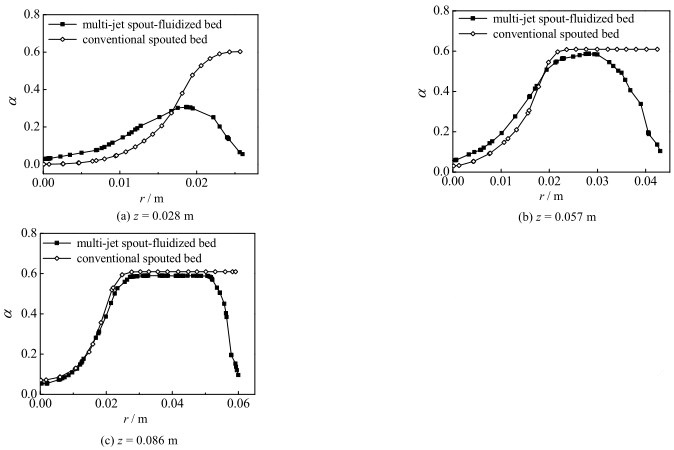
图 6给出了两种喷动床在不同床层高度处颗粒体积分数沿径向的分布规律。由图可知,两种喷动床在喷射区的颗粒体积分数接近零,其中常规喷动床的颗粒体积分数随着径向距离的增加呈现出先增大后趋于稳定值的规律,而多喷嘴喷动-流化床的颗粒体积分数呈现出波动分布并存在颗粒浓度的局部峰值现象。在床层高度为z = 0.028 m处,多喷嘴喷动-流化床环隙区颗粒的体积分数达到最小并接近零,且颗粒体积分数呈现近似直线分布规律,说明多喷嘴结构对喷动床柱锥区内颗粒堆积的破坏作用尤为明显,能有效地流化柱锥区内颗粒流动死区,对于喷动床内颗粒的均匀流化起到了显著效果。随着床层高度的增加(图 6(b),(c)),由于侧喷嘴气体对柱锥区堆积颗粒的强烈流化作用及能量耗散,以及轴向空间距离的增加,使得流化气体对高床层处环隙区内颗粒的流化作用逐渐减弱。此时,多喷嘴喷动-流化床内的颗粒浓度的分布规律逐渐接近常规喷动床。
|
图 6 不同床层高度下两种喷动床内颗粒体积分数径向分布对比 Fig.6 Comparison of particle concentrations at different bed heights in the two spouted beds |
为了进一步考察关键设计参数对整体式多喷嘴喷动-流化床内气固两相流动规律的影响,在多喷嘴喷动-流化床侧壁开孔数量(24)、入口气体流量保持不变的情况下,进一步分析侧壁开孔直径对多喷嘴喷动-流化床内气固两相流动规律的影响。多喷嘴喷动-流化床的主喷嘴直径保持为24 mm,Ai/Az值分别设定为0.042、0.167、0.375、0.67、1.042 (即侧喷嘴圆孔直径设计为1、2、3、4和5 mm)。在达到稳定喷动的情况下,图 7为多喷嘴喷动-流化床内颗粒的体积分数云图。由图可知,喷泉高度随着侧喷嘴直径的增大而有所增加,当侧喷嘴与主喷嘴横截面积比Ai /Az=0.67时,多喷嘴喷动-流化床所形成的喷动效果最好。

|
图 7 不同开孔直径下多喷嘴喷动-流化床内颗粒体积分数云图分布对比 Fig.7 Particle volume fraction distribution under different multi-jet diameters in the multi-jet spout-fluidized bed |
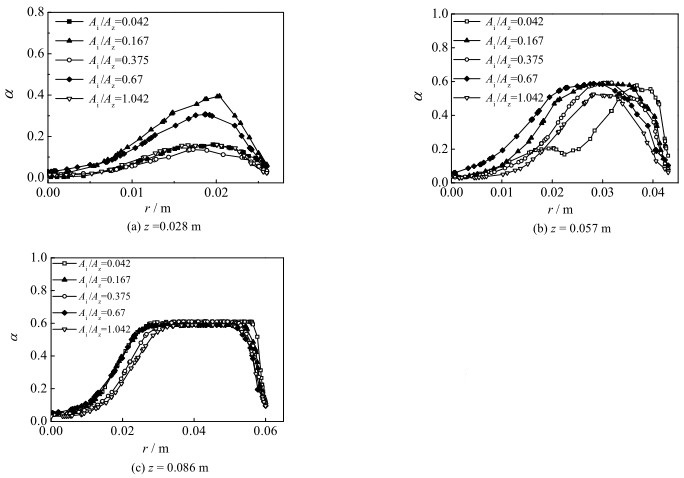
图 8为在不同床层高度下,侧喷嘴开孔直径大小对颗粒体分数径向分布的影响。由图可知,从喷射区到环隙区颗粒的体积分数呈现出轴对称的先增大后减小趋势,在喷动床近壁面处由于侧喷嘴气流的局部流化作用,颗粒浓度值呈现出显著的下降趋势。当进气横截面积比Ai /Az=0.042时,环隙区颗粒的浓度呈现出最小值状态;而当Ai /Az=0.167时,环隙区颗粒浓度值达到最大。整体而言,侧喷嘴的气体的分流作用减少了喷动床环隙区颗粒的堆积及流动死区,有利于实现颗粒体积分数径向分布实现均匀化。
|
图 8 不同床层高度下开孔直径对颗粒体积分数径向分布规律影响 Fig.8 Effects of multi-jet diameter on particle volume fraction at different bed heights in the spout-fluidized bed |
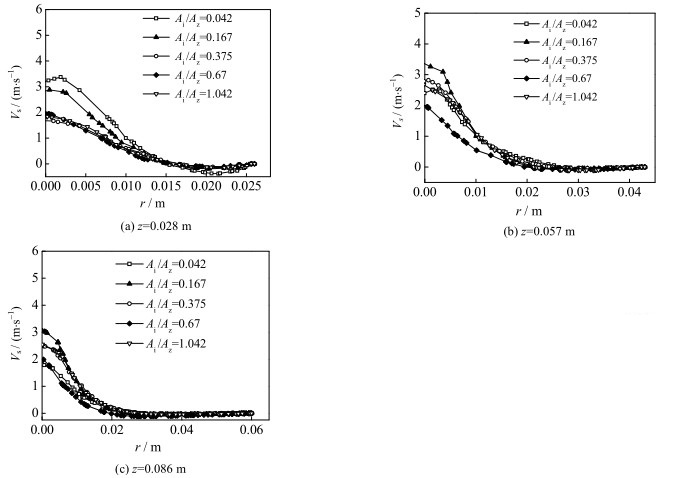
图 9为不同床层高度下,喷动床柱锥壁面开孔直径对颗粒速度径向分布的影响情况。由图可知颗粒速度在喷射区达到最大,随着径向距离的增大,颗粒速度呈现出逐渐减小的趋势。在低床层区z=0.028 m处,喷射区颗粒的速度随着开孔直径的增加而降低,即Ai/Az= 0.042时,颗粒速度达到最大值。这是由于开孔直径较小时,气体的主体流量集中在主喷嘴,直接加速了颗粒的轴向运动速度。随着柱锥侧壁开孔直径逐渐增大,侧壁开孔气体的分流及对颗粒的径向流化作用逐渐增强,消耗了进口气体的一部分动能,从而削弱了主喷嘴进口气体对喷动床颗粒轴向运动的影响。在床层高度为z= 0.057 m及z= 0.086 m处,无量纲进气横截面积比为Ai /Az=0.167时,多喷嘴喷动-流化床喷射区内的颗粒速度高于其它工况。
|
图 9 不同床层高度下开孔直径对颗粒速度径向分布规律影响 Fig.9 Effects of multi-jet diameter on particle velocity radial distribution at different bed heights in the spout-fluidized bed |
为了进一步定量分析多喷嘴结构对喷动床内颗粒群的流化效应,采用相对标准偏差(CV)作为颗粒流场均匀度指标。CV为无量纲变量,可以用来比较均值明显不同的总体离散性,也可以比较流场均匀性的改善程度:
| ${\rm{CV}} = (S/\bar V) \times 100\% $ | (10) |
| $S = \sqrt {\frac{1}{{n - 1}}\sum\limits_{j = 1}^n {{{({V_j} - \bar V)}^2}} } $ | (11) |
式中:S为标准偏差;Vj为第j个采样点的速度值;V为所有采样点的平均速度;n为采样点个数。通过比较不同工况下的CV值来评判流场的均匀度,CV值越小,流场均匀度越高。
如图 10为不同床层高度下,进气横截面积比Ai /Az对喷动-流化床内颗粒速度场均匀度CV的影响。由图可知颗粒流场CV值随着床层高度的增加而上升,且随着Ai /Az值的增加呈现出一定的波动变化规律,并在Ai /Az=0.67附近达到了极小值。表明多喷嘴结构对颗粒流场的均匀化效应主要体现在喷动床柱锥区。综合床层的各个高度情况并对CV值进行平均分析发现,当Ai /Az=0.67时,喷动-流化床内整体颗粒流场的均匀度为最优状态,即侧喷嘴对喷动-流化床内整体的颗粒流化作用达到最佳。

|
图 10 不同床层高度下Ai /Az对颗粒速度分布均匀性影响对比 Fig.10 Comparison of CV of particle velocity at different bed heights in the multi-jet spout-fluidized bed |
(1) 相比较于常规喷动床,多喷嘴喷动床结构能够有效流化喷动床柱锥区的颗粒流动死区,对于喷动床内颗粒的均匀流化起到了积极作用,加强了喷动床内气体、颗粒的径向运动混合。
(2) 在低床层区,喷射区颗粒的速度随着开孔直径的增加而降低,随着柱锥侧壁开孔直径逐渐增大,削弱了主喷嘴进口气体对喷动床颗粒轴向运动的影响。在高床层区,当Ai /Az=0.167时,多喷嘴喷动-流化床喷射区内的颗粒速度达到极值。
(3) 颗粒速度场的均匀度CV随着床层高度的增加而上升,表明多喷嘴对颗粒流场的均匀化效应主要体现在喷动床柱锥区。当Ai /Az=0.67时,侧喷嘴对喷动-流化床内整体的颗粒流化作用达到最佳。
(4) 可进一步研究分析侧壁开孔密度(数量)、不同的开孔形状、侧孔分布形式等因素对多孔喷动–流化床内气固两相流动特性的影响规律。
| 符号说明: | |||
| AZ | -主喷嘴横截面积,m2 | Res | -相对雷诺数 |
| Ai | -侧喷嘴总横截面积,m2 | S | -标准偏差 |
| CV | -相对标准偏差 | t | -时间,s |
| D | -喷动床柱体直径,mm | U | -主喷嘴气体喷动速度,m·s-1 |
| CD | -曳力系数 | Ums | -主喷嘴气体最小的喷动速度,m·s-1 |
| Di | -主喷嘴入口直径,mm | V | -所有采样点的平均速度 |
| dP | -颗粒直径,mm | Vs | -颗粒速度,m·s-1 |
| g | -重力加速度,m·s-2 | Vj | -第j个采样点的速度值,m·s-1 |
| H | -固定床高,m | x, y, z | -坐标轴 |
| H0 | -静床层高度,m | α | -气体或颗粒体积分数 |
| Kgs | -相间动量交换系数 | τg | -气体应力张量 |
| m | -开孔个数 | τs | -颗粒应力张量 |
| pg | -气体压力,Pa | μg | -气体黏度,Pa·s |
| Δp | -床层总压降,kPa | δ | -侧壁开孔直径,mm |
| R | -喷动床柱体半径,mm | ρ | -气体或颗粒的密度,kg·m-3 |
| r | -喷动床径向距离,mm | v | -气体或颗粒速度矢量,m·s-1 |
| [1] |
SEROWIK M, FIGIEL A, NEJMAN M, et al. Drying characteristics and some properties of spouted bed dried semi-refined carrageenan[J]. Journal of Food Engineering, 2017, 194: 46-57. DOI:10.1016/j.jfoodeng.2016.09.007 |
| [2] |
ERKIAGA A, LOPEZ G, AMUTIO M, et al. Influence of operating conditions on the steam gasification of biomass in a conical spouted bed reactor[J]. Chemical Engineering Journal, 2014, 237(2): 259-267. |
| [3] |
ZHANG S, LI L, WANG J, et al. Experimental research of semi-dry flue gas simultaneous desulfurization and denitrification with spouted bed[J]. Chinese Journal of Environmental Engineering, 2011, 5(8): 1847-1851. |
| [4] |
朱卫兵, 邢力超, 孙巧群, 等. 基于双流体模型的烟气喷动床脱硫过程的数值模拟[J]. 中国矿业大学学报, 2012, 41(1): 7-13. ZHU W B, XING L C, SUN Q Q, et al. Numerical simulation of flue gas desulfurization in a spouted bed based on two-fluid model[J]. Journal of China Mining University, 2012, 41(1): 7-13. |
| [5] |
何玉荣, 孙巧群, 陆慧林, 等. 贴体坐标系下喷动床内气固两相流体动力特性的数值模拟[J]. 燃烧科学与技术, 2006, 12(1): 59-64. HE Y R, SUN Q Q, LU H L, et al. Gas-solid flow simulations in spouted beds on body-fitted coordination[J]. Journal of Combustion Science and Technology, 2006, 12(1): 59-64. DOI:10.3321/j.issn:1006-8740.2006.01.013 |
| [6] |
金涌, 祝京旭, 汪展文, 等. 流态化工程原理[M]. 北京: 清华大学出版社, 2001. JIN Y, ZHU J X, WANG Z W, et al. Fluidization engineering principles[M]. Beijing: Tsinghua University Press, 2001. |
| [7] |
WANG S, ZHAO L, WANG C, et al. Numerical simulation of gas-solid flow with fluid model in a spouted-fluid bed[J]. Particuology, 2014, 14(3): 109-116. |
| [8] |
何晶亮, 袁先程, 廖纪军, 等. 整体式多喷嘴喷动-流化床内气固两相流动规律数值模拟[J]. 高校化学工程学报, 2017, 31(6): 1340-1348. HE J L, YUAN X C, MIAO J J, et al. Numerical simulation of gas-solid two-phase flow in a novel integral multi-nozzle spout-fluidized bed[J]. Journal of Chemical Engineering of Chinese Universities, 2017, 31(6): 1340-1348. DOI:10.3969/j.issn.1003-9015.2017.00.034 |
| [9] |
WANG Q, LUO J L, XU C H. Numerical simulation of the gas-particle flow behavior in oil shale semi-coke spouted bed[J]. Energy Procedia, 2012, 17: 892-900. DOI:10.1016/j.egypro.2012.02.184 |
| [10] |
LIBARDI B P, XAVIER T P, LIRA T S, et al. Fluid dynamic analysis for pyrolysis of macadamia shell in a conical spouted bed[J]. Powder Technology, 2016, 299: 210-216. DOI:10.1016/j.powtec.2016.05.034 |
| [11] |
MARTINS G Z, SOUZA C R F, SHANKAR T J, et al. Effect of process variables on fluid dynamics and adhesion efficiency during spouted bed coating of hard gelatin capsules[J]. Chemical Engineering & Processing, 2008, 47(12): 2238-2246. |
| [12] |
GONIVA C, KLOSS C, DEEN N G, et al. Influence of rolling friction on single spout fluidized bed simulation[J]. Particuology, 2012, 10(5): 582-591. DOI:10.1016/j.partic.2012.05.002 |
| [13] |
YANG S L, LUO K, ZHANG K, et al. Numerical study of a lab-scale double slot-rectangular spouted bed with the parallel CFD-DEM coupling approach[J]. Powder Technology, 2015, 272: 85-99. DOI:10.1016/j.powtec.2014.11.035 |
| [14] |
HOSSEINI S H, FATTAHI M, AHMADI G. Hydrodynamics studies of a pseudo 2D rectangular spouted bed by CFD[J]. Powder Technology, 2015, 279: 301-309. DOI:10.1016/j.powtec.2015.04.013 |
| [15] |
QIU K Z, HU C S, YANG S L, et al. Computational evaluation of depth effect on the hydrodynamics of slot-rectangular spouted bed[J]. Powder Technology, 2016, 287: 51-60. DOI:10.1016/j.powtec.2015.09.034 |
| [16] |
HOSSEINI S H, FATTAHI M, AHMADI G. CFD study of hydrodynamic and heat transfer in a 2D spouted bed:Assessment of radial distribution function[J]. Journal of the Taiwan Institute of Chemical Engineers, 2016, 58: 107-116. DOI:10.1016/j.jtice.2015.06.027 |
| [17] |
TAKABATAKE K, MORI Y, KHINAST J G, SAKAI M. Numerical investigation of a coarse-grain discrete element method in solid mixing in a spouted bed[J]. Chemical Engineering Journal, 2018, 346: 416-426. DOI:10.1016/j.cej.2018.04.015 |
| [18] |
HE Y L, QIN S Z, LIM C J, et al. Particle velocity profiles and solid flow patterns in spouted beds[J]. Canadian Journal of Chemical Engineering, 1994, 72(4): 561-568. DOI:10.1002/cjce.5450720402 |
| [19] |
HE Y L, LIM C J, GRACE J R, et al. Measurements of voidage profiles in spouted beds[J]. Canadian Journal of Chemical Engineering, 1994, 72(2): 229-234. DOI:10.1002/cjce.5450720208 |
| [20] |
WU F, GAO W, ZHANG J, et al. Numerical analysis of gas-solid flow in a novel spouted bed structure under the longitudinal vortex effects[J]. Chemical Engineering Journal, 2018, 334: 2105-2114. DOI:10.1016/j.cej.2017.11.166 |




