2. 山东省特种设备检验研究院有限公司,山东 济南 250101
2. Shandong Special Equipment inspection institute Co., Ltd., Jinan 250101, China
天然气作为一种清洁能源,可以降低二氧化碳、二氧化硫、氮氧化物等气体的排放量,在工业和生活上具有重要的应用价值[1]。标准状态下,同质量的天然气其液态的体积仅有气态的1/625,因此液化天然气对于天然气储存和运输过程具有重要意义。天然气由非共沸气体(沸点-162 ℃的甲烷,沸点-88 ℃的乙烷,沸点-42 ℃的丙烷,沸点-196 ℃的氮气等)组成,由于各组分沸点差距较大,为降低工艺过程的㶲损失需要对不同沸点的组分进行分级冷凝。而在分级冷凝的最后阶段,即甲烷冷凝阶段,氮气作为不凝结气体而存在。现已证明不凝气体存在降低冷凝传热效率,导致传热恶化[2]。因此探究甲烷和氮气混合气体的冷凝机理,对于厘清混合气体冷凝过程的传热传质机理以及优化设计换热器具有重要意义。
目前,关于含不凝气体的蒸汽冷凝对流传热已有大量研究[3],其研究方法主要有理论分析、实验研究和数值模拟。NUSSELT在1916年提出了膜状冷凝模型,通过模型简化得到了纯蒸汽层流膜状冷凝的理论解,并总结出纯蒸汽在无限大竖直平板上进行膜状冷凝传热的主要热阻为液膜的导热热阻。而关于含不凝气体的冷凝,DONALD[4] 首先对含空气的水蒸汽在水平管内的冷凝进行了实验研究,发现ϕB = 0.5%的不凝气体会使传热系数下降近50%。之后,MINKOWYCZ[5] 对竖直壁面上含空气的水蒸气冷凝进行了理论分析,发现传热热阻主要为混合气体层的扩散阻力,而界面热阻是次要热阻。然而由于温度限制,关于超低温流体冷凝的实验及数据较为匮乏,并主要以氮气或氧气等纯蒸汽为冷凝工质[6-9]。在常压下,饱和甲烷蒸汽温度很低且易燃,其作为冷凝工质对实验设备的耐低温要求很高且具有较高的危险性,因此采用数值计算的方法更加经济有效。
一些学者基于CFD方法对含不凝气的蒸汽冷凝进行数值研究[10-17]。LI等[10]以及李晓伟等[11]利用“壁面反应”模型研究了水平管内含不凝气的蒸汽冷凝,忽略了液膜厚度增加对管径的减小效应,其结果与实验对比有较大误差。刘泉[12]利用VOF方法对管内和平板上含空气的水蒸汽冷凝进行数值模拟,其模型忽略了气液界面上的质量传递,不能很好地解释两相之间传递现象。YIN等[13]、WU等[14]和SHEN [15]利用LEE模型计算冷凝速率,对含空气的水蒸气进行模拟研究。但是LEE模型的经验系数受工况影响,不易确定选值的合理性。本文以商业软件ANSYS FLUENT为平台,利用VOF模型处理两相流动,使用组分输运模型计算相内扩散传质,基于扩散模型自定义UDF迭代求解扩散函数,计算冷凝相变的质量与能量源相。得到了冷凝过程的传热传质特性,以及液膜与混合气体层的分布规律,可以为强化含不凝气的蒸汽冷凝的流动与传热设计计算提供重要的依据。
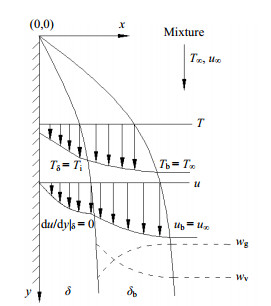
2 数值模型在二维大空间中,处于饱和温度的甲烷与氮气的混合气体自上而下流经低温竖直壁面,并在壁面上发生膜状凝结。在甲烷蒸汽冷凝过程中,靠近低温壁面处的甲烷蒸汽含量随着冷凝的进行而逐渐降低,而氮气作为不凝结气体在近壁面处逐渐聚集形成滞留的混合气膜层。在混合气膜层内,靠近主流区的蒸汽和气液界面上蒸汽之间存在浓度梯度,从而驱动甲烷蒸汽向气液界面扩散。随着冷凝的进行,在液膜附近不断积聚的氮气使蒸汽含量下降、传质距离增加,当冷凝与对流扩散速率相等时,整个流动传热传质过程达到稳定状态。根据NUSSELT的膜状冷凝理论,液膜层内热传递的主要机制是导热,而在混合气膜层传递的主要机制则是对流传热和质量扩散。因此相比于纯蒸汽的冷凝过程,含不凝气的蒸汽在冷凝时会在冷凝液外侧形成具有一定浓度梯度的混合气膜层,其带来的传质阻力使冷凝过程的传热系数大大降低。为研究含不凝气蒸汽冷凝的传热传质特性,采用二维无限大等温竖直平板作为对象,以氮气-甲烷蒸气混合物为工质进行研究。基本物理模型如图 1所示。
|
图 1 传热传质模型 Fig.1 Heat and mass transfer models used in the study |
研究对象为给定入口速度的沿竖直无限大平板的冷凝流动模型,并对模型进行如下假设:稳态,常物性;气液两相均为层流流动;气液界面上没有温度、速度阶跃;壁面是光滑的等温壁面,且无滑移,无接触热阻;氮气不能渗透进入液膜;气相主流区域的速度和温度是均匀的且等于入口值;气相区不会自发产生液滴。由于模型为无限大平板,可以忽略压力变化对液相和气相影响,认为气液两相均为不可压缩流体。
液膜层内的流动为不可压缩、无内热源的二维定常流动,其质量方程、动量方程及能量方程分别为:
| $\frac{\partial }{{\partial x}}\left( {{\rho _\text{l}}u} \right) + \frac{\partial }{{\partial y}}\left( {{\rho _\text{l}}v} \right) = {S_\text{m}}$ | (1) |
| ${\rho _\text{l}}\left( {{u_\text{l}}\frac{{\partial {u_\text{l}}}}{{\partial x}} + v\frac{{\partial {u_\text{l}}}}{{\partial y}}} \right) = \left( {{\rho _\text{l}} - {\rho _\infty }} \right)g + {\mu _\text{l}}\frac{{{\partial ^2}{u_\text{l}}}}{{\partial {y^2}}}$ | (2) |
| ${\rho _\text{l}}{c_\text{pl}}\left( {{u_\text{l}}\frac{{\partial T}}{{\partial x}} + {v_\text{l}}\frac{{\partial T}}{{\partial y}}} \right) = {k_\text{l}}\frac{{{\partial ^2}{T_\text{l}}}}{{\partial {y^2}}} + {S_\text{h}}$ | (3) |
混合气体的质量守恒方程、动量守恒方程、能量守恒方程以及扩散方程分别如下:
| $\frac{\partial }{{\partial x}}\left( {{\rho _\text{m}}u} \right) + \frac{\partial }{{\partial y}}\left( {{\rho _\text{m}}v} \right) = - {S_\text{m}}$ | (4) |
| ${\rho _\text{m}}\left( {u\frac{{\partial u}}{{\partial x}} + v\frac{{\partial u}}{{\partial y}}} \right) = \left( {{\rho _\text{m}} - {\rho _\infty }} \right)g + {\mu _\text{m}}\frac{{{\partial ^2}u}}{{\partial {y^2}}}$ | (5) |
| ${\rho _\text{m}}{c_\text{p}}\left( {u\frac{{\partial T}}{{\partial x}} + v\frac{{\partial T}}{{\partial y}}} \right) = \lambda \frac{{{\partial ^2}T}}{{\partial {y^2}}} + \left( {{c_{{p_\text{v}}}} - {c_{{p_\text{g}}}}} \right){j_\text{g}}\frac{{\partial T}}{{\partial y}} - {S_\text{h}}$ | (6) |
| ${\rho _\text{m}}\left( {u\frac{{\partial {w_\text{v}}}}{{\partial x}} + v\frac{{\partial {w_\text{v}}}}{{\partial y}}} \right) = - \frac{{\partial {j_\text{v}}}}{{\partial y}}$ | (7) |
式中,Sm和Sh分别为由于甲烷蒸汽冷凝而产生的质量源相和能量源相。式(2)和(5)分别为液、气两相的动量守恒方程,其右侧第1项均为密度差引起的浮升力,并由主流区密度与当地密度之差决定。式(3)和(6)分别为液、气两相的能量守恒方程,液相的传递机制主要为液膜层的对流传热,而气相除对流传热外还有质量传递引起的热扩散,即式(6)右侧的第2项。式(7)为忽略了热扩散项的气相扩散方程。
2.2 相变及传质模型VOF多相流模型是基于欧拉-欧拉方法,通过表面追踪来得到气液两相之间自由界面的。以体积分数来表示计算网格内气液两相所占比例,且单个网格内气液两相的体积分数之和为1,通过求解体积分数方程式(9)追踪气液界面。模型中,将混合气体和液态甲烷分别设置为初始相和第2相:当气相体积分数Fm = 0时,网格被液相充满;当Fm = 1时,网格被混合气体充满;当0 < Fm < 1时,网格内气液共存。
| ${F_\text{m}} + {F_\text{l}} = 1$ | (8) |
| $\nabla \left( {{F_\text{m}}\rho \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u} } \right) = {\dot m_\text{cond}}$ | (9) |
扩散模型选取组分输运模型中的两组分扩散传质,采用FICK定律计算扩散速率,如式(10)所示。假设混合气体为理想气体,根据分子运动理论,采用式(11)计算扩散系数[18],其中Ωij为分子碰撞积分。
| ${j_i} = \rho {D_{ij}}\frac{{\partial {w_i}}}{{\partial y}}$ | (10) |
| ${D_{ij}} = 0.0018583\sqrt {{T^3}\left( {\frac{1}{{{M_i}}} + \frac{1}{{{M_j}}}} \right)} \frac{1}{{p\sigma _{ij}^2{\Omega _{\text{D}, ij}}}}$ | (11) |
假设整个传热传质过程是处于平衡状态的,则界面上的蒸汽冷凝速率应该等于蒸汽通过混合气体层的扩散速率。因此,根据界面上的质量守恒,蒸汽的冷凝速率可以表示为
| ${\dot m_\text{cond}} = {j_\text{v}} + {\rho _\text{v}}u$ | (12) |
根据式(9)和(12)可求解网格内的液相体积分数,从而得到当地的冷凝速率。相应地,冷凝质量源相和能量源相分别为Sm和Sh。
| ${S_\text{m}} = {\dot m_\text{cond}}\frac{A}{{{V_\text{cell}}}}$ | (13) |
| ${S_\text{h}} = {\dot m_\text{cond}}\frac{A}{{{V_\text{cell}}}}{h_\text{fg}}$ | (14) |
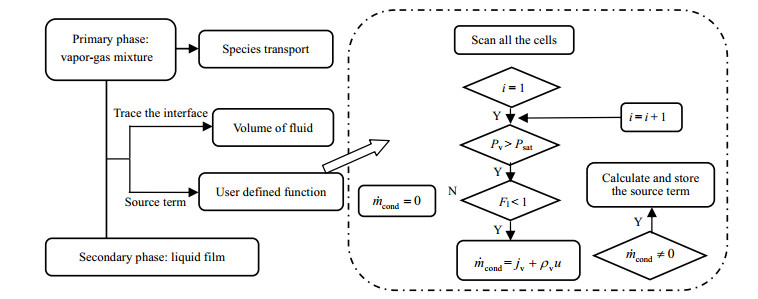
模型通过自定义UDF来求解计算网格内的冷凝源相,如图 2,其基本思路为:首先识别靠近壁面的第1层(i = 1)网格,判断网格内压力是否达到相应温度下甲烷蒸汽冷凝的饱和压力,若达到冷凝条件则计算并储存冷凝源相;然后判断第(i + 1)层网格,重复上述计算,直至网格当前网格内源相值为0,停止迭代。
|
图 2 计算模型 Fig.2 Flow chart of the calculation procedure |
通过对甲烷蒸汽饱和曲线进行拟合,得到饱和压力与温度的函数关系(适用温度为90 ~120 K)如下:
| ${p_\text{sat}} = - 1.96597 \times {10^6} + 67852.9T - 792.645{T^2} + 3.14149{T^3}$ | (15) |
计算域内的混合相的物性参数是根据当地气液两相的体积分数求得的,密度、动力黏度、导热系数以及比热容分别为:
| $\mathit{\Phi} = {F_\text{m}}{\mathit{\Phi} _\text{m}} + {F_\text{l}}{\mathit{\Phi} _\text{l}}{, _{}}\mathit{\Phi} = \rho , \mu , k$ | (16) |
| ${c_p} = \frac{1}{\rho }{F_\text{m}}{\rho _\text{m}}{c_\text{pm}} + {F_\text{l}}{\rho _\text{l}}{c_\text{pl}}$ | (17) |
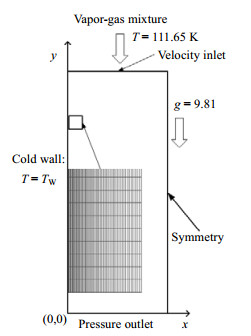
模型的计算域网格划分如图 3所示,在近壁面处对网格进行了加密处理。上部边界为速度入口,下部边界为压力出口,左侧为恒温冷壁面,右侧设置为对称边界。通过网格的独立性验证,选取7万网格数作为计算网格,既能保证结果的准确性又可以节省计算时间。采用隐式算法求解稳态方程组,使用PISO算法求解压力速度耦合项,动量、能量以及组分方程均使用二阶迎风格式进行离散,而体积分数使用一阶迎风格式,压力使用PRSTO!格式进行离散。由于数值模型同时使用了VOF和组分输运模型,因此需要随时调节松弛因子以达到收敛。模型通过检测低温壁面的平均传热系数以及控制域内液相体积分数是否达到稳定值,来判断模拟是否收敛。
|
图 3 计算域网格划分 Fig.3 Mesh distribution on the computational domain |
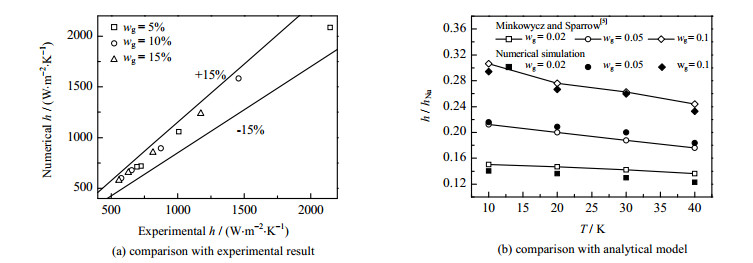
由于关于含氮气的甲烷蒸汽冷凝的实验和模拟目前未见报道,因此为验证数值模型的正确性,以水蒸汽和空气为介质进行了模拟计算,并与YI等[19] 的实验结果以及MINKOWYCZ [5] 的分析解进行了对比验证。YI对尺寸为100 mm × 50 mm的竖直壁面上含空气的水蒸气的冷凝过程进行了实验研究,冷凝壁面温度为333~383 K,入口空气wB = 5% ~ 50%,冷凝实验段的压力为0.1 MPa。利用数值计算模型,对一个大气压下,入口空气wB = 2% ~15%,壁面过冷度为10 ~ 50 K的几种工况进行了计算。模拟结果与实验以及分析解的结果对比如图 4所示。可以发现,模拟与实验结果的误差在15%以内,且换热系数的变化趋势与分析解一致。模型的预测值及其变化趋势与实验及分析解均吻合较好,所以认为模型是可靠的。
|
图 4 模型验证 Fig.4 Verification of the model |
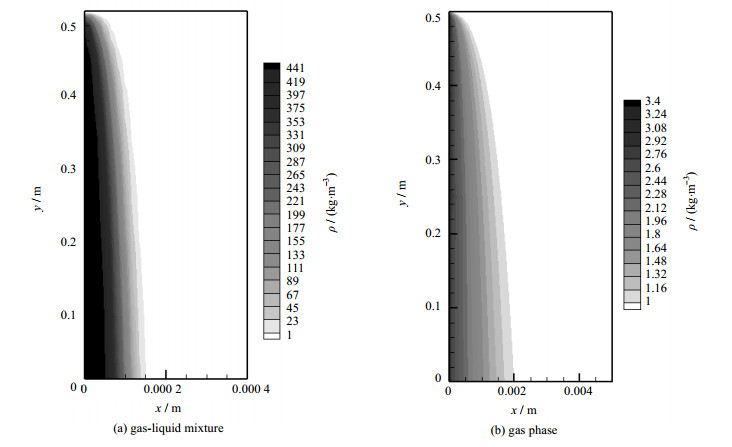
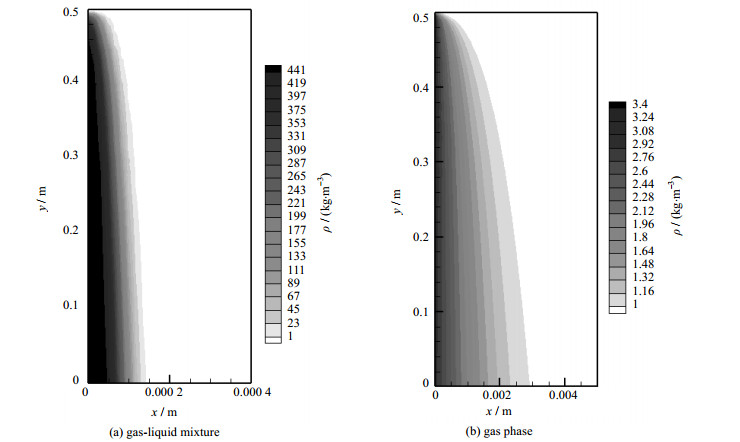
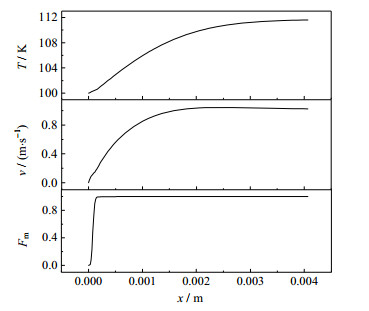
图 5和6为过冷度为10 K、压力0.1 MPa、氮气w(N2) = 3.441%和16.249%工况下的液相和气相密度分布云图。图 5(a)和6(a)均为混合相的密度分布云图,从图中可以看出贴近冷壁面处为冷凝液膜其密度最大,而远离液膜处为混合气体其密度最小。另外,可以发现沿着流动方向(y轴反方向)液膜逐渐发展变厚然后趋于稳定。图 5(b)和图 6(b)均为气相的密度分布云图,靠近冷壁面处氮气含量最高故其密度最大,外侧区域为主流混合气体,而中间具有密度梯度的区域为混合气膜层。这是由于氮气不能渗透进入液膜层,所以会在气液界面上不断地积聚,从而与主流区域形成浓度差。同样地,气膜层也是沿着流动方向逐渐发展增厚的。另外,通过对比图 5和图 6可以发现,不凝气体含量的增加会削减液膜层的厚度,同时使混合气膜层增厚。相同条件下液膜的减薄会使液相热阻降低,而不凝气含量的增加以及混合气膜层的变厚会使得气相扩散热阻增加。另外,从气液两相的坐标尺寸上可以发现,混合气膜层的厚度远远大于液膜厚度图 7为氮气w(N2) = 16.249%、壁面过冷度为10 K时,截面y = 0.2 m处的温度、速度以及气相体积分数曲线。从图中可以看到,靠近原点处Fm < 1的区域为液膜,其对应的温度和速度基本都是线性增加的;而混合气膜层内温度和速度的增加速率都是逐渐降低的,直至与主流区达到一致。因此在液膜层内的传热机制主要为导热,这与NUSSELT理论相符合。而在混合气膜层,由于黏滞应力作用使得气液界面上没有产生温度及速度阶跃;混合气膜层内受温度差和浓度差的影响会出现速度波动,但这种影响在靠近主流区域处逐渐降低并趋近于零,最终使速度与主流区域相一致。
|
图 5 w(N2) = 3.441%,ΔT = 10 K时,气液两相密度分布云图 Fig.5 Density contours of liquid and gas mixture at w(N2) = 3.441%, ΔT = 10 K |
|
图 6 w(N2) = 16.249%,ΔT = 10 K,气液两相密度分布云图 Fig.6 Density contours of liquid and gas mixture at w(N2) = 16.249%, ΔT = 10 K |
|
图 7 y = 0.2 m处温度、速度和气相体积分数分布图 Fig.7 Distribution of temperature, velocity and liquid volume fraction at y = 0.2 m |
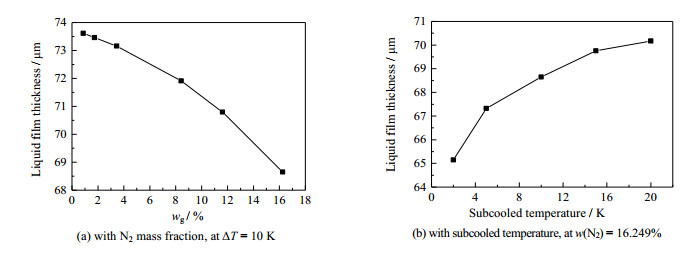
在含不凝气蒸汽的冷凝过程中,主要热阻位置分别在冷凝液膜以及混合气膜层内。为探究其传热传质规律,对平均液膜厚度以及平均混合气膜层厚度在不同氮气含量以及壁面过冷度下的变化规律进行了分析,如图 8和9所示。由于常物性条件下k为常数,根据努谢尔特理论,当液膜内主要传热机制为导热时,热阻大小与液膜厚度呈正相关。图 8(a)为ΔT = 10 K时,冷凝液膜的平均厚度随氮气质量分数的变化曲线。可以发现随着氮气含量的增加液膜厚度逐渐变薄,说明不凝气的增加可以削减液膜层的厚度。这是由于不凝气体的增加使得蒸汽通过混合气体层的扩散阻力增加,从而降低了蒸汽的冷凝速率;另外,不凝气的积聚会增加液膜表面的扰动,更利于液膜的排除,从而使液膜厚度减薄。图 8(b)为w(N2) = 16.249%时,冷凝液膜的平均厚度随壁面过冷度的变化曲线。当过冷度从2变化到20 K时,液膜厚度逐渐增加且增加速度逐渐变缓,这说明过冷度的增加使得液膜热阻增大、传热效率降低,且在低过冷度时这种影响更加明显。
|
图 8 不同工况下,平均液膜厚度的变化规律 Fig.8 Profiles of average liquid film thickness at different conditions |
|
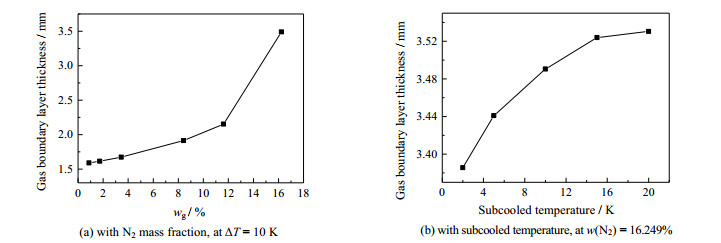
图 9 不同工况下,混合气膜厚度的变化规律 Fig.9 Profiles of average gas layer thickness at different conditions |
根据式(10),当浓度差一定时,扩散系数与扩散距离呈负相关。图 9(a)为ΔT = 10 K时,平均混合气膜层厚度(氮气w(N2) = 16.3%处)随入口氮气含量的变化曲线。随着入口氮气含量的增加气膜层厚度明显增加,且氮气含量越高其影响越明显。这说明不凝气体含量的增加会使传质阻力大大增加。图 9(b)为w(N2) = 16.249%时,平均混合气膜层厚度(氮气w(N2) = 16.3%处)随壁面过冷度的变化曲线。可以发现随着过冷度的增加气膜厚度逐渐增加且增加速度逐渐减缓
综上,不凝气体含量的增加虽然在一定程度上会减薄液膜层从而使液膜导热热阻降低,但使得混合气膜层的扩散热阻成倍增加;壁面过冷度的增加会使液膜和混合气膜的厚度同时增加,导致传热系数降低,而这种影响在过冷度较低时更明显。
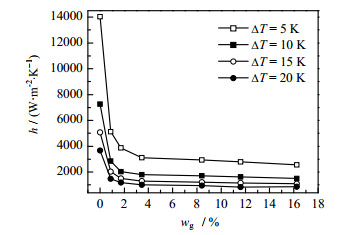
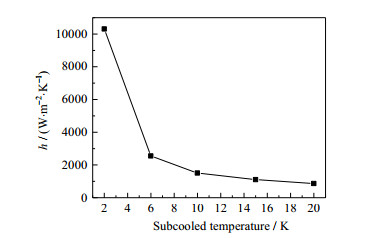
图 10为不同过冷度下,壁面的平均冷凝传热系数随主流氮气质量分数的变化曲线。从图中可以看出,不凝气体含量的增加会使得传热系数降低。当ΔT = 10 K、入口氮气质量分数从0增加到3.441%时,冷凝传热系数下降了约70%。但随着不凝气含量的增加,传热系数的下降速度逐渐趋缓,这主要是因为不凝结气体在液膜附近的累积阻碍了蒸汽的扩散。图 11为w(N2) = 16.249%时,平均冷凝传热系数随壁面过冷度的变化曲线。由图可以发现,过冷度的增加会使传热系数降低,且随着过冷度的增加其降低速度趋缓,这与气膜与液膜的变化规律一致。
|
图 10 不同过冷度下,平均冷凝传热系数随主流不凝气质量分数的变化规律 Fig.10 Profiles of average heat transfer coefficient under different mass fractions at different ΔT |
|
图 11 w(N2) = 16.249%时,平均传热系数随壁面过冷度的变化规律 Fig.11 Average heat transfer coefficient as a function of subcooled temperature at w(N2) = 16.249% |
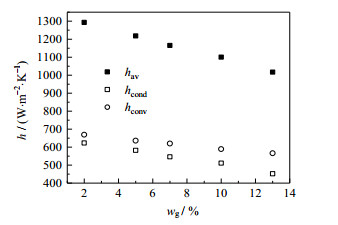
图 12为不同氮气含量下平均换热系数、平均冷凝换热系数和平均对流换热系数随不凝气体含量变化的规律。三者均随不凝气质量分数的增加而降低,但是冷凝换热系数所占的比重逐渐下降。这说明不凝气体的增加会在低温壁面与主流气体之间滞留形成扩散阻碍层,从而降低了蒸汽的冷凝速率,导致系统的换热效率下降。根据宿吉强[20]的研究,在含空气的水蒸气冷凝时,潜热是显热的两倍左右,当空气含量大于50%时显热逐渐超过潜热起主要作用。含氮气的甲烷冷凝过程中,显热在不凝气含量较低时即比潜热略高,且比重不断增加。这说明当不凝气比蒸汽的分子量小时,不凝气体更加容易积聚,从而阻碍冷凝换热。
|
图 12 平均传热系数随不凝气含量的变化规律 Fig.12 Average heat transfer coefficient as a function of mass fraction at ΔT = 15 K |
本文建立了含氮气的甲烷蒸汽冷凝过程的传热传质模型,利用数值计算的方法进行了求解,得到了以下结论:
(1) 氮气的存在会导致甲烷蒸汽的冷凝传热系数大幅下降,当ΔT = 10 K、入口氮气质量分数从0增加到3.441%时,冷凝传热系数下降了约70%。
(2) 在冷凝液膜的外侧存在着具有浓度梯度的混合气膜层。在计算工况下,混合气膜层的厚度比液膜层的厚度大两个数量级,气膜层内的扩散阻力对换热的降低起到了主要作用。
(3) 氮气含量的增加虽然使液膜层厚度减薄,但同时会使混合气膜层厚度成倍增加,从而使冷凝换热恶化;壁面过冷度的增加会使得液膜和混合气膜的厚度同时增加,并且这种影响在过冷度较低时更加明显。
符号说明:
|
|
| [1] |
LIM W, CHOI K, MOON I. Current status and perspectives of liquefied natural gas (LNG) plant design[J]. Industrial & Engineering Chemistry Research, 2013, 52(9): 3065-3088. |
| [2] |
HIJIKATA K, CHEN S J, TIEN C L. Non-condensable gas effect on condensation in a two-phase closed thermosyphon[J]. International Journal of Heat and Mass Transfer, 1984, 27(8): 1319-1325. DOI:10.1016/0017-9310(84)90059-0 |
| [3] |
HUANG J, ZHANG J, WANG L. Review of vapor condensation heat and mass transfer in the presence of non-condensable gas[J]. Applied Thermal Engineering, 2015, 89(Supplement C): 469-484. |
| [4] |
OTHMER D F. The condensation of steam[J]. Industrial & Engineering Chemistry, 1929, 21(6): 576-581. |
| [5] |
MINKOWYCZ W J, SPARROW E M. Condensation heat transfer in the presence of noncondensables, interfacial resistance, superheating, variable properties, and diffusion[J]. International Journal of Heat and Mass Transfer, 1966, 9(10): 1125-1144. |
| [6] |
LEONARD R J, TIMMERHAUS K D. Condensation studies of saturated nitrogen vapors[J]. Advances in Cryogenic Engineering, 1970, 15(11): 308-315. |
| [7] |
HASELDEN G, PROSAD S. Heat transfer from condensing oxygen and nitrogen vapors[J]. Transactions of the Institution of Chemical Engineers, 1949, 27: 195-200. |
| [8] |
LIN L H L, YUAO D, SUN Z, et al. A study on the condensation heat transfer of the saturated nitrogen vapor inside the v-type fluted tube[J]. Journal of Zhejiang University, 1985, 19(4): 53-61. |
| [9] |
OHIRA K. Laminar film condensation heat transfer of hydrogen and nitrogen inside a vertical tube[J]. Heat Transfer - Asian Research, 2001, 30(7): 542-560. DOI:10.1002/(ISSN)1523-1496 |
| [10] |
LI J D. CFD simulation of water vapor condensation in the presence of non-condensable gas in vertical cylindrical condensers[J]. International Journal of Heat and Mass Transfer, 2013, 57(2): 708-721. DOI:10.1016/j.ijheatmasstransfer.2012.10.051 |
| [11] |
李晓伟, 吴莘馨, 何树延. 含不凝性气体冷凝对流传热传质过程的数值模拟[J]. 工程热物理学报, 2013, 34(2): 302-306. LI X W, WU X X, HE S Y. Numerical simulation of the heat and mass transfer process of convective condensation with non-condensable gas[J]. Journal of Engineering Thermophysics, 2013, 34(2): 302-306. |
| [12] |
刘泉.纯蒸气及含不凝气蒸气冷凝的数值研究[D].合肥: 中国科学技术大学, 2015. LIU Quan. Numerical investigation on condensation with and without non-condensable gas[D]. Hefei: University of Science and Technology of China, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10358-1015615597.htm |
| [13] |
YIN Z, WEN J, WU Y, et al. Effect of non-condensable gas on laminar film condensation of steam in horizontal minichannels with different cross-sectional shapes[J]. International Communications in Heat and Mass Transfer, 2016, 70: 127-131. DOI:10.1016/j.icheatmasstransfer.2015.11.008 |
| [14] |
WU X M, LI T, LI Q, et al. Approximate equations for film condensation in the presence of non-condensable gases[J]. International Communications in Heat and Mass Transfer, 2017, 85(Supplement C): 124-130. |
| [15] |
SHEN Q, SUN D, SU S, et al. Development of heat and mass transfer model for condensation[J]. International Communications in Heat & Mass Transfer, 2017, 84: 35-40. |
| [16] |
刘纳, 李俊明. R32在水平微细圆管内凝结换热的数值模拟[J]. 化工学报, 2014, 65(11): 4246-4253. LIU N, LI J M. Numerical simulation of R32 condensation heat transfer in horizontal circular microchannel[J]. CIESC Journal, 2014, 65(11): 4246-4253. DOI:10.3969/j.issn.0438-1157.2014.11.005 |
| [17] |
余园园, 杨犁, 彭昌军, 等. 分子动力学模拟不同类型MOFs材料对NO2气体扩散影响[J]. 高校化学工程学报, 2018, 32(4): 823-830. YU Y Y, YANG L, PENG C J, et al. Molecular dynamic simulation on effects of MOFs type on NO2 diffusivity[J]. Journal of Chemical Engineering of Chinese Universities, 2018, 32(4): 823-830. DOI:10.3969/j.issn.1003-9015.2018.04.011 |
| [18] |
BIRD R B. Transport Phenomena[M]. New York: ASME, 2002: R1-R4.
|
| [19] |
YI Q, TIAN M, YAN W, et al. Visualization study of the influence of non-condensable gas on steam condensation heat transfer[J]. Applied Thermal Engineering, 2016, 106(Supplement C): 13-21. |
| [20] |
宿吉强, 王辉, 孙中宁. 含空气蒸汽冷凝传热特性数值模拟[J]. 化工学报, 2014, 65(9): 3425-3433. SU J Q, WANG H, SUN Z N. Numerical simulations for steam condensation in presence of air[J]. CIESC Journal, 2014, 65(9): 3425-3433. DOI:10.3969/j.issn.0438-1157.2014.09.016 |




