2. 西安交通大学 动力工程多相流国家重点实验室,陕西 西安 710049
2. State Key Laboratory of Multiphase Flow in Power Engineering, Xi'an Jiaotong University, Xi'an 710049, China
复杂化学工业的流程主要包括化工原料管理、生产加工工艺、设备运行监测和维修维护、废弃物排放及应急措施管理等环节,表现为工艺、设备、仪表耦合多样,高温、高压、深冷等极端环境频发,运行工况和操作环境多变,从原料、中间体到成品,大多具有易燃易爆、毒性等化学危险性,间接造成了化工行业事故的多发性和严重性。而回看化学工业的安全生产历史,严重灾难的发生往往并不是一个孤立事件,尽管事故可能具有突发性和偶然性,却常常是微小故障量积累和诱发的结果。化工行业作为按模式计划生产且规则一贯式的作业,工艺、设备等重复性的故障和风险是不可避免的。
在实际化工过程的数据采集系统中,各类传感器可获取丰富的数据信息,通过对比、分析正常运行工况和不同故障模式下的数据即可实现基于数据驱动的故障诊断[1-2]。然而,高维度、海量的传感器原始数据对基于数据驱动的故障诊断方法造成了一定影响,称为“维数灾难”。对高维数据直接进行处理,不仅消耗计算资源,而且造成拟合模型精确度不足,背离了实际生产的需求。为解决这一问题,常用的数据特征提取和维度降低方法有独立成分分析(independent component correlation algorithm, ICA)、主元分析(principal component analysis, PCA)、线性判别分析(linear discriminant analysis, LDA)等。ICA是一种从多维统计数据中寻找隐含变量的方法,其假设原始数据中隐变量彼此独立,能有效提取过程数据中的多模态和非高斯特性,广泛应用于多工况过程[3]及化工过程[4]的数据降维和故障诊断中。但由于实际过程中数据分布规律往往较为复杂,呈现出高斯和非高斯关联的情况,单一采用ICA贡献度的诊断方法易导致准确率不高。PCA是指在特征提取时,使原始数据在投影子空间的各个维度的方差最大化。PCA及其改进算法核主元分析(kernel principal component analysis, KPCA)在工业过程软测量[5]和故障监测诊断领域[6-8]取得了良好效果,但PCA是基于全局信息实现,属于非监督学习,在对数据本身完全无知的情况下,无法最大化地保留有价值信息并揭示不同类别数据的本质特征。而LDA方法已广泛应用于滚动轴承[9]和复杂工业[10]等领域的故障诊断和回归预测。郭金玉等[11]将基于局部Fisher判别分析(local fisher discriminant analysis, LFDA)算法应用于TE (Tennessee Eastman)过程,使用K近邻(K-nearest-neighbor, KNN)算法将映射至特征子空间的原始数据进行故障分类,提高了传统方法的灵敏性和准确性。马立玲等[12]提出一种基于改进核Fisher的故障分类的方法,有效改善了核Fisher的投影效果,并减少了故障样本的诊断错误率,同样在TE化工仿真过程得以验证。以上方法主要是针对LDA算法本身进行特定优化,用于直接对多模态故障数据进行特征子空间投影,以达到明显的多模态故障分类效果,而后通过分类算法辅助提升故障检测的准确率,是将LDA方法直接用于诊断,而非探究其对数据预处理的作用,未研究不同投影维度数对故障诊断准确率及灵敏度的影响。为此,本文提出一种基于线性判别分析与支持向量机(support vector machine, SVM)融合的化工过程故障诊断方法,利用化工领域工程师对历史故障的评判、分析、归类等先验知识,将LDA用于原始数据的预处理阶段,剔除冗余信息,使用低维故障样本作为SVM的输入值,同时结合网格搜索法与K折交叉验证理论,建立高精度故障诊断模型,从而及时、准确地排除重复性隐患。同时应用TE化工仿真过程的测试结果验证该法的有效性。
2 线性判别分析LDA,又称Fisher判别分析,是一类有监督学习的分类和降维方法,能够有效利用原始数据的类别信息,进行准确的特征提取,通过寻求投影变换,达到类间相异度高,类内相似度高的效果,使得它在特征提取方面更加高效[13]。
如图 1所示,给定训练集样本数据,设法将原始数据投影到一条直线上。选择不同直线w得到的映射效果不同。LDA方法需要找到这样一条直线,使得同类样例的投影点尽可能接近,异类样例的投影点尽可能远离,从而有效地解决多分类的问题。
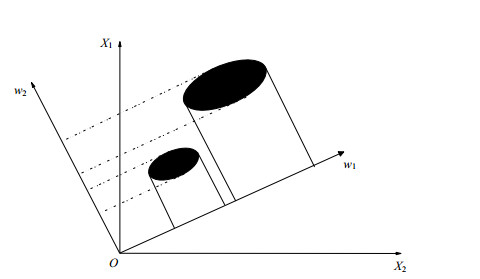
|
图 1 LDA映射原理 Fig.1 LDA mapping method |
假定存在N类样本,xi表示第i类样本的集合,且第i类样本的示例数为mi,yi则表示第i类样本经投影后的集合,原始数据样本表示为x = {x1, x2, …, xN},LDA投影后的样本表示为y = {y1, y2, …, yN}。
样本的均值向量μ为
| $\mathit{\boldsymbol{\mu}} {\rm{ = }}\frac{{\rm{1}}}{N}\sum\limits_{i = 1}^m {{\mathit{\boldsymbol{x}}_i}} {\rm{ }}i = 1, \ldots , N$ | (1) |
定义样本的全局散度矩阵St为
| ${\mathit{\boldsymbol{S}}_\text{t}} = {\mathit{\boldsymbol{S}}_\text{w}} + {\mathit{\boldsymbol{S}}_\text{b}} = \sum\limits_{i = 1}^m {(\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{\mu}} _i})} {(\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{\mu}} _i})^\text{T}}$ | (2) |
其中Sw是类内散度矩阵,Sb是类间散度矩阵。
样本的类内离散度矩阵Sw为
| ${\mathit{\boldsymbol{S}}_\text{w}} = \sum\limits_{i = 1}^N {\sum\limits_{x \in {X_i}} {(\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{\mu}} _i})} } {(\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{\mu}} _i})^\text{T}}$ | (3) |
则样本的类间散度矩阵Sb为
| ${\mathit{\boldsymbol{S}}_\text{b}} = {\mathit{\boldsymbol{S}}_\text{t}} - {\mathit{\boldsymbol{S}}_\text{w}} = \sum\limits_{i = 1}^N {{\mathit{\boldsymbol{m}}_i}({\mathit{\boldsymbol{\mu}} _i} - \mathit{\boldsymbol{\mu}} )} {({\mathit{\boldsymbol{\mu}} _i} - \mathit{\boldsymbol{\mu}} )^\text{T}}$ | (4) |
采用Fisher准则函数优化:
| $J(\mathit{\boldsymbol{W}}) = \frac{{{\mathit{\boldsymbol{W}}^\text{T}}{\mathit{\boldsymbol{S}}_\text{b}}\mathit{\boldsymbol{W}}}}{{{\mathit{\boldsymbol{W}}^\text{T}}{\mathit{\boldsymbol{S}}_\text{w}}\mathit{\boldsymbol{W}}}}$ | (5) |
通过广义特征值问题求解Fisher准则函数的最大值为
| ${\mathit{\boldsymbol{S}}_\text{b}}\mathit{\boldsymbol{W}} = \lambda {\mathit{\boldsymbol{S}}_\text{w}}\mathit{\boldsymbol{W}}$ | (6) |
由于投影矩阵W的闭式解是
支持向量机作为一种基于统计学习理论的机器学习算法,在诸如模式识别[14]等领域有广泛应用。SVM通过寻求结构风险最小化,以提高模型的学习泛化能力,实现经验风险和置信范围权衡下的最优化,从而获取全局最优解。故障诊断的本质是一个分类问题,原始故障数据的产生即为监督学习的过程,因此,基于SVM相关的方法同样在工业软测量[15]、故障诊断[16-17]等领域得到了广泛的关注。
支持向量机的核心思想是在高维特征空间中找到一个令样本数据线性分开的划分超平面,使得正反两类数据之间的距离最大化。对于在样本空间中线性可分的二类问题,假设给定训练样本集
| ${\mathit{\boldsymbol{W}}^\text{T}}\mathit{\boldsymbol{x}} + \mathit{\boldsymbol{b}} = 0$ | (7) |
其中
| $\text{MIN}_{\mathit{\boldsymbol{w}}, \mathit{\boldsymbol{b}}} = \frac{1}{2}{\left\| \mathit{\boldsymbol{w}} \right\|^2}{\rm{ }}{\rm{s}}{\rm{.t}}{\rm{.}}{\rm{ }}{\mathit{\boldsymbol{y}}_i}({\mathit{\boldsymbol{w}}^\text{T}}{x_i} + \mathit{\boldsymbol{b}}) \geqslant 1, {\rm{ }}i = 1, \ldots , m$ | (8) |
引入拉格朗日乘子
| $L(\mathit{\boldsymbol{w}}, \mathit{\boldsymbol{b}}, \mathit{\boldsymbol{a}}) = \frac{1}{2}{\left\| \mathit{\boldsymbol{w}} \right\|^2} + \sum\limits_{i = 1}^m {{\alpha _i}(1 - {\mathit{\boldsymbol{y}}_i}({w^\text{T}}{\mathit{\boldsymbol{x}}_i} + \mathit{\boldsymbol{b}}))} $ | (9) |
其中
| $f(x) = {\rm{sgn}}(\sum\limits_{i = 1}^m {{a_i}{\mathit{\boldsymbol{y}}_i}\mathit{\boldsymbol{x}}_i^\text{T}\mathit{\boldsymbol{x}} + \mathit{\boldsymbol{b}}} )$ | (10) |
在样本数据非线性的情况下,可通过引入预先定义好的内积函数将数据从原始空间映射到高维特征空间,从而将线性学习器拓展为非线性学习器。预先定义好的内积函数称为核函数,应用不同的核函数构造的支持向量机性能不同[18],常用的核函数有以下几类:
(1) Linear线性核函数
| $K({\mathit{\boldsymbol{x}}_i}, {\mathit{\boldsymbol{x}}_j}) = \mathit{\boldsymbol{x}}_i^\text{T}{\mathit{\boldsymbol{x}}_j}$ | (11) |
(2) Polynomial多项式核函数
| $K({\mathit{\boldsymbol{x}}_i}, {\mathit{\boldsymbol{x}}_j}) = {(\gamma \mathit{\boldsymbol{x}}_i^\text{T}{\mathit{\boldsymbol{x}}_j} + r)^d}$ | (12) |
(3) Radial basis function(RBF)高斯径向核函数
| $K({\mathit{\boldsymbol{x}}_i}, {\mathit{\boldsymbol{x}}_j}) = {\rm{exp}}{( - \gamma \left\| {{\mathit{\boldsymbol{x}}_i}} \right. - {\mathit{\boldsymbol{x}}_j})^2}{\rm{ }}\gamma > 0{\rm{ }}$ | (13) |
(4) Sigmoid核函数
| $K({\mathit{\boldsymbol{x}}_i}, {\mathit{\boldsymbol{x}}_j}) = {\rm{tanh}}(\gamma \mathit{\boldsymbol{x}}_i^\text{T}{\mathit{\boldsymbol{x}}_j} + \gamma )$ | (14) |
网格搜索法[19] (grid search, GS)是一种调整模型超参数的方法,属于穷举类算法。其原理是在所有候选参数中,通过在一定范围内划分网格,遍历循环网格内所有点,尝试每一种可能性,并计算其约束函数和目标函数的值。对满足约束条件的点,逐个比较其目标函数的值,抛弃坏的点,保留好的点,最后得到最优解的近似解。
K折交叉验证[19] (K-fold cross validation, K-CV)原理是随机地将已给数据切分为K组互不相交、规模相同的子集,然后利用K-1个子集的数据作为训练集,余下的一个子集作为测试集,即可获得K组训练集/测试集,最后返回使得K组测试结果中平均误差最小的一组超参数。
SVM模型拥有众多可调参数,且这些参数对模型最终结果起着关键作用。因此,对SVM进行参数寻优十分必要。为了评价每次选出参数的好坏,需要选择评价指标,这里选取查准率(accuracy)为评价指标。同时,为了避免初始数据划分对结果的影响,引入交叉验证方式减少偶然性,这里采用网格搜索和K折交叉验证相结合的方法。
5 TE过程故障诊断实验TE过程是美国Tennessee Eastman化学公司提出的一个实际化工过程的仿真数据集[20],广泛用于化工过程故障诊断的模拟研究验证。TE过程主要分为反应器、冷凝器、压缩机、分离器和汽提塔5个单元,包括A、B、C、D、E、F、G和H等8种主要成分,有41个测量变量和12个控制变量,共53个测量变量,预设21类故障,其中16类已知型故障和5类未知型故障。
故障1~7为阶跃干扰,例如冷却水入口温度或者进料成分的变化;故障8~12为随机变化型干扰;故障13是反应动力学中的缓慢漂移干扰;故障14和15为堵塞型干扰;故障16~21为未知型干扰。
5.1 故障样本选取选取正常工况、故障1、5、7、12和17作为研究对象,涵盖了常见的阶跃、随机以及未知干扰型的故障类型,如表 1所示。
在训练集中,稳态无故障运行的仿真周期为48 h,采样时间间隔为3 min,产生观测值960组;故障运行的仿真周期为48 h,故障在8 h的时候引入,共采集960个观测值,其中后800个观测值为故障数据。本文选取训练数据集为正常工况800 × 52,故障工况5 × 800 × 52,其中5指5类故障模式、800指样本数,52指变量数。在测试集中,稳态无故障运行的仿真周期为25 h,产生样本500组;故障运行的仿真周期为24 h,共有480个观测值。故本文选取测试数据集为正常工况500 × 52,故障工况5 × 480 × 52。
5.2 故障诊断过程(1) 数据收集和预处理。从TE过程获取原始数据并划分为训练集和测试集,将包括相应故障数据标签的训练集与测试集分别组合,产生训练数据集矩阵4 800 × 52,测试数据集矩阵2 900 × 52,是正常运行工况和五类故障数据的并集。诊断流程见图 2。
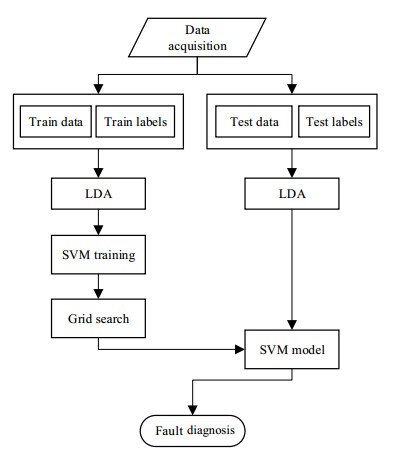
|
图 2 故障诊断流程 Fig.2 Fault diagnosis flowchart |
(2) 特性提取和数据降维。将训练集数据通过LDA算法投射到低维特征空间,进行故障特征提取,并将正常工况和5组故障类型由52维度降低至不超过5维,可视化特征提取效果并初步分析。为了说明在建立SVM模型前引入LDA的优势,对6组运行工况的数据进行维度可视化处理。图 3(a)表示六类运行工况52维度原始数据混合叠加在一起,基本无法辨识,而数据经过LDA处理后的数据聚散情况较为分明,如图 3(b)~(d)所示,分别是将原始数据压缩降低至5维度、4维度、3维度下的部分数据2D分布散点图。显然,低维的数据集群清晰可分,存在一定规律性,意味着LDA算法在故障特征提取中有着较好的性能。
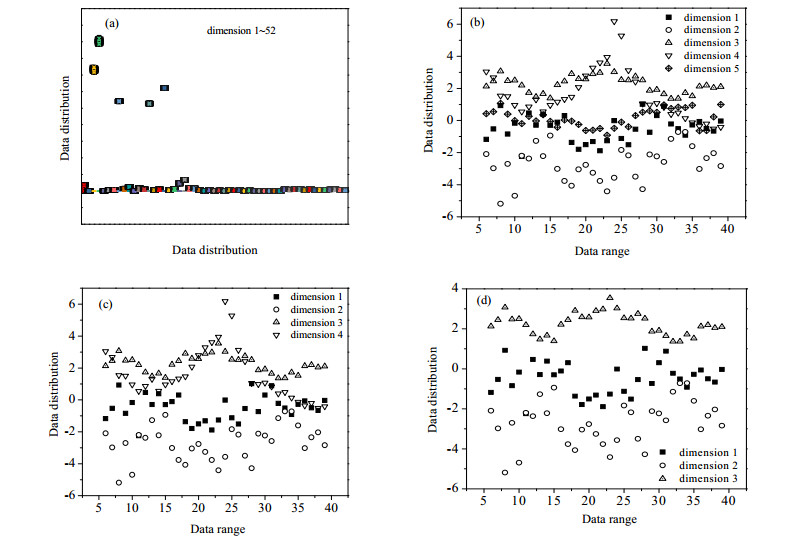
|
图 3 数据维度可视化 Fig.3 Data dimension visualization |
(3) 设计SVM,通过训练集数据准确拟合出故障诊断模型。在模型建立后初步对训练数据维度数和准确率的关系进行趋势研究。如图 4所示,可以看出特征提取后数据为5维度时,诊断准确率最为优良。因此,确定LDA算法的投射维度为5。
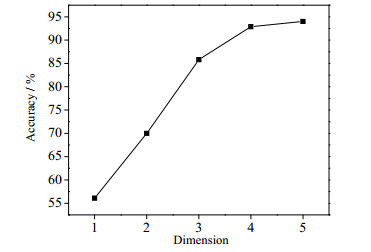
|
图 4 数据维度与准确率的关系 Fig.4 Effect of data dimension on accuracy |
(4) 通过网格搜索法及K折交叉验证,搜索最佳的SVM模型。超参数惩罚系数C和核函数系数γ值的不同将影响SVM故障诊断方法的性能,将训练集通过对K折交叉验证法划分出一部分作为验证集,进行参数搜索,以期得到最佳性能。由图 3可知,5维度下的故障数据耦合交织在一起,呈非线性分布,故SVM模型采用RBF核函数,以解决非线性多分类的故障诊断问题。如图 5所示,在约束条件内通过网格搜索法得到RBF核函数下的最优超参数组合为{C = 4.7,γ = 0.14}。此时在训练集上的识别准确率达到95.8%,大幅优于默认参数。
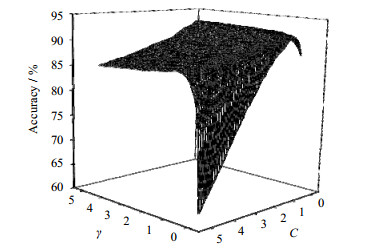
|
图 5 SVM参数优化 Fig.5 SVM parameter optimization |
(5) 输入LDA处理后的测试集数据并可视化故障诊断结果,在测试集上的故障诊断准确率达到93.9%,效果良好,未产生明显的欠拟合或过拟合效应。在机器学习中,混淆矩阵是以一个特定的矩阵呈现算法性能的可视化效果,能够刻画分类器的分类准确程度。矩阵每列代表预测值,每行代表的是实际类别。对于正常工况、故障1、5、7、12和17联合诊断结果如图 6混淆矩阵所示。以图中第2行为例,其横坐标为1,是指对在以故障1模式下仿真运行的480组数据进行故障诊断,判断为故障1的正确结果有471组数据、为正常工况0的有3组数据、为故障12的有6组数据,故仅针对故障1识别率达到了98.1%。
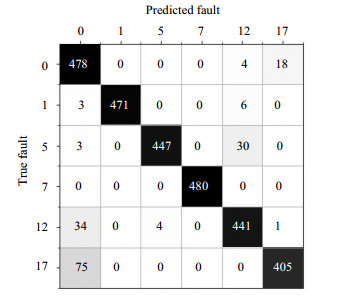
|
图 6 故障诊断混淆矩阵 Fig.6 Confusion matrix of fault diagnosis |
结合LDA特征提取,基于GS参数优化和K折交叉验证的SVM故障诊断方法在TE过程仿真中取得了较好的效果。另外,同样对比引入网格搜索方法和K折交叉验证后,在最优参数选取下的单一SVM和PCA_SVM算法,有计算速度快、故障诊断准确率更高的优势,如表 2所示。
|
|
表 2 故障诊断方法对比 Table 2 Comparison of fault diagnosis methods |
通过将LDA与SVM融合方法应用于化工过程多分类故障诊断中,最大限度地利用已有故障的先验知识,在保留故障特征的条件下,采用LDA有效降低了化工过程高维数据。然后应用GS方法和K折交叉验证搜索并建立最佳超参数的SVM模型,从而迅速、精准地定位类似重复故障所在,及时地保障安全生产。以TE化工仿真过程中混合正常工况和五类故障模式下的原始高维数据进行验证,新方法对5类运行模式下的故障平均诊断率达到93.9%;同时,与SVM、PCA_SVM方法相比,故障识别率有一定提升,收敛速度也相对加快,表明该方法能有效解决复杂化工过程中的故障诊断问题。
|
|
| [1] |
钱锋, 杜文莉, 钟伟民, 等. 石油和化工行业智能优化制造若干问题及挑战[J]. 自动化学报, 2017, 43(6): 893-901. QIAN F, DU W L, ZHONG W M, et al. Problems and challenges of smart optimization manufacturing in petrochemical industries[J]. Acta Automatica Sinica, 2017, 43(6): 893-901. |
| [2] |
XIE Y, ZHANG T. A fault diagnosis approach using SVM with data dimension reduction by PCA and LDA method[C]//Chinese Automation Congress. Wuhan: IEEE, 2016.
|
| [3] |
徐莹, 邓晓刚, 钟娜. 基于ICA混合模型的多工况过程故障诊断方法[J]. 化工学报, 2016, 67(9): 3793-3803. XU Y, DENG X G, ZHONG N. A fault diagnosis method for multimode processes based on ICA mixture models[J]. CIESC Journal, 2016, 67(9): 3793-3803. |
| [4] |
薄翠梅, 乔旭, 张广明, 等. 基于ICA-SVM的复杂化工过程集成故障诊断方法[J]. 化工学报, 2009, 60(9): 2259-2264. BO C M, QIAO X, ZHANG G M, et al. ICA-SVM based fault diagnosis method for complex chemical process[J]. CIESC Journal, 2009, 60(9): 2259-2264. DOI:10.3321/j.issn:0438-1157.2009.09.018 |
| [5] |
李桂香, 王磊, 李继定, 等. 基于PCA-LSSVM的氢回收膜分离过程建模[J]. 高校化学工程学报, 2013, 27(5): 877-883. LI G X, WANG L, LI J D, et al. Modeling of hydrogen recovery membrane separation process based on PCA-LSSVM[J]. Journal of Chemical Engineering of Chinese Universities, 2013, 27(5): 877-883. |
| [6] |
常玉清, 王姝, 王福利, 等. 基于多PCA模型的过程监测方法[J]. 仪器仪表学报, 2014, 35(4): 901-908. CHANG Y Q, WNAG S, WANG F L, et al. Process monitoring method based on multiple PCA models[J]. Chinese Journal of Scientific Instrument, 2014, 35(4): 901-908. |
| [7] |
郭金玉, 刘玉超, 李元. 一种基于改进局部熵PCA的工业过程故障检测方法[J]. 高校化学工程学报, 2019, 33(4): 922-932. GUO J Y, LIU Y C, LI Y. A fault detection method based on improved local entropy PCA for industrial processes[J]. Journal of Chemical Engineering of Chinese Universities, 2019, 33(4): 922-932. DOI:10.3969/j.issn.1003-9015.2019.04.019 |
| [8] |
何菲, 杜文莉, 钱锋. PCA_SVM的多故障分类方法在TE过程中的应用[J]. 计算机与应用化学, 2010, 27(10): 1321-1324. HE F, DU W L, QIAN F. Multifaults classification method based on PCA_SVM and its application to the TE process[J]. Computers and Applied Chemistry, 2010, 27(10): 1321-1324. DOI:10.3969/j.issn.1001-4160.2010.10.005 |
| [9] |
黄大荣, 陈长沙, 孙国玺, 等. 复杂装备轴承多重故障的线性判别分析与反向传播神经网络协作诊断方法[J]. 兵工学报, 2017, 38(8): 1649-1657. HUANG D R, CHEN C S, SUN G X, et al. Linear discriminant analysis and back propagation neural network cooperative diagnosis method for multiple faults of complex equipment bearings[J]. Acta Armamentarii, 2017, 38(8): 1649-1657. DOI:10.3969/j.issn.1000-1093.2017.08.024 |
| [10] |
成忠, 诸爱士, 陈德钊. ISOMAP-LDA方法用于化工过程故障诊断[J]. 化工学报, 2009, 60(1): 122-126. CHENG Z, ZHU A S, CHEN D Z. Fault diagnosis of chemical process using isometric feature mapping and linear discriminant analysis[J]. CIESC Journal, 2009, 60(1): 122-126. DOI:10.3321/j.issn:0438-1157.2009.01.018 |
| [11] |
郭金玉, 韩建斌, 李元, 等. 基于局部Fisher判别分析的复杂化工过程故障诊断[J]. 计算机应用研究, 2018, 35(4): 1122-1125, 1129. GUO J Y, HAN J B, LI Y, et al. Fault diagnosis of complex chemical process based on local Fisher discriminant analysis[J]. Application Research of Computers, 2018, 35(4): 1122-1125, 1129. DOI:10.3969/j.issn.1001-3695.2018.04.035 |
| [12] |
马立玲, 徐发富, 王军政. 一种基于改进核Fisher的故障诊断方法[J]. 化工学报, 2017, 68(3): 1041-1048. MA L L, XU F F, WANG J Z. A fault diagnosis method based on improved kernel Fisher[J]. CIESC Journal, 2017, 68(3): 1041-1048. |
| [13] |
盛立东. 模式识别导论[M]. 北京: 北京邮电大学出版社, 2010. SHENG L D. Introduction to pattern recognition[M]. Beijing: Beijing University of Posts and Telecommunications Press, 2010. |
| [14] |
GUO G, LI S Z, CHAN K. Face recognition by support vector machines[C]//Automatic Face and Gesture Recognition, 2000. Proceedings. Fourth IEEE International Conference. Grenoble: IEEE, 2000.
|
| [15] |
颜立伟, 余云松, 李云, 等. 吸收法捕集二氧化碳过程的离子浓度软测量[J]. 化工学报, 2010, 61(5): 1169-1175. YAN L W, YU Y S, LI Y, et al. Soft-sensing study of ion concentration in process of carbon dioxide capture by absorption[J]. CIESC Journal, 2010, 61(5): 1169-1175. |
| [16] |
张建, 李艳军, 曹愈远, 等. 免疫支持向量机用于航空发动机磨损故障诊断[J]. 北京航空航天大学学报, 2017, 43(7): 1419-1425. ZHANG J, LI Y J, CAO Y Y, et al. Immune SVM used in wear fault diagnosis of aircraft engine[J]. Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(7): 1419-1425. |
| [17] |
徐可, 陈宗海, 张陈斌, 等. 基于经验模态分解和支持向量机的滚动轴承故障诊断[J]. 控制理论与应用, 2019, 36(6): 915-922. XU K, CHEN Z H, ZHANG C B, et al. Rolling bearing fault diagnosis based on empirical mode decomposition and support vector machine[J]. Control Theory & Applications, 2019, 36(6): 915-922. |
| [18] |
HSU C W, LIN C J. A Comparison of methods for multiclass support vector machines[J]. IEEE Transactions on Neural Networks, 2002, 13(2): 415-425. DOI:10.1109/72.991427 |
| [19] |
李航. 统计学习方法[M]. 北京: 清华大学出版社, 2012. LI H. Statistical learning method[M]. Beijing: Tsinghua University Press, 2012. |
| [20] |
DOWNS J J, VOGEL E F. A plant-wide industrial process control problem[J]. Computers & Chemical Engineering, 1993, 17(3): 245-255. |




