压滤机是广泛应用于环保、化工、制药、洗煤等行业的固液分离设备[1],提高其过滤效率、降低能耗具有重要的节能减排意义。压滤过程通常为全封闭过程,滤室内料浆的流动形态、滤饼的发展规律难以被直接观测,料浆与滤饼对滤板的挤压效应难以被直接在线监测。因此压滤工艺参数设置、滤板结构设计等仍主要依靠经验。
压滤机通常配有数十至上百块滤板并由油缸压紧形成封闭的滤室,在压滤过程中料浆的流动形态主要受进料流量、过滤面积、料浆黏度等参数的影响。而料浆通常为以细颗粒为主的多相流体,其黏度主要取决于颗粒间作用力的大小,而且当颗粒浓度增大到一定程度时,颗粒间开始出现黏着、摩擦以及碰撞等效应,使多相流体黏度升高,流变性质不再符合牛顿线性流变方程[2-3],即此时的多相流体呈现出拟塑性特点,已不属于牛顿流体[4]。
前期关于压滤过程的研究,如谭蔚[5]、耿亚梅[6]应用Fluent软件对新型动态扫流板框压滤机滤室中流体流动形态进行了数值模拟研究并进行了实验室小试,其数值模拟结果与实验结果良好吻合,说明其采用的数值模拟方法具有良好的可行性。文献[7-10]则在上述方法的基础上分别研究了不同结构的压滤机及滤板,分析了压滤过程中滤室内压力分布、速度分布以及过滤效率等。
然而上述文献均以单滤室模型作为分析对象,过滤面积与滤室容积比整机缩小数十倍,却仍以整机的实际进料流量作为入口流量,使得数值模拟中的进料流量与过滤面积及滤室容积不匹配,计算结果与实际必然存在较大差距。且上述文献对含颗粒多相流体的颗粒间作用力研究较少甚至未做考虑,也必然导致高浓度区域的流动形态与实际不符。
针对上述问题,本文以文献[5-6]中数值模拟方法为基础,以1250型滤板内煤浆压滤脱水过程为研究对象,通过比例缩减进料流量并统筹考虑固-液两相间曳力及煤粒间作用力,数值模拟厢式压滤机压滤过程,研究煤粒浓度、直径等参数对煤浆流动性能的影响,分析煤粒沉积成饼规律与滤室内压力分布规律。
2 压滤脱水过程的数学模型 2.1 煤浆的多相流模型煤浆是典型的固-液两相流体系,其液相材料为水,密度ρl = 998.2 kg·m-3,固相材料为煤并定义为颗粒,密度ρs = 1200 kg·m-3。
| $ \frac{\partial }{{\partial t}}\left( {{\alpha _{\rm{s}}}{\rho _{\rm{s}}}{{\vec v}_{\rm{s}}}} \right) + \nabla \cdot \left( {{\alpha _{\rm{s}}}{\rho _{\rm{s}}}{{\vec v}_{\rm{s}}}{{\vec v}_{\rm{s}}}} \right) = - {\alpha _{\rm{s}}}\nabla p - \nabla {p_{\rm{s}}} + \nabla \cdot {{\bar {\bar \tau} }_{\rm{s}}} + {\alpha _{\rm{s}}}{\rho _{\rm{s}}}\vec g + \\ {K_{{\rm{ls}}}}\left( {{{\vec v}_{\rm{l}}} - {{\vec v}_{\rm{s}}}} \right) + \left( {{{\vec F}_{\rm{s}}} + {{\vec F}_{{\rm{lift,s}}}} + {{\vec F}_{{\rm{vm,s}}}} + {{\vec F}_{{\rm{td,s}}}}} \right) $ | (1) |
式中,p为体系压力,
| $ {{\bar {\bar \tau} }_{\rm{s}}}{\rm{ = }}{\alpha _{\rm{s}}}{\mu _{\rm{s}}}\left( {\nabla {{\vec v}_{\rm{s}}}{\rm{ + }}\nabla \vec v_{\rm{s}}^{\rm{T}}} \right) + {\alpha _{\rm{s}}}\left( {{\lambda _{\rm{s}}} - \frac{{\rm{2}}}{3}{\mu _{\rm{s}}}} \right)\nabla \cdot {{\vec v}_{\rm{s}}}\bar {\bar I} $ | (2) |
式中,
| $ {\lambda _{\rm{s}}}{\rm{ = }}\frac{{\rm{4}}}{{\rm{3}}}\alpha _{\rm{s}}^{\rm{2}}{\rho _{\rm{s}}}{d_{\rm{s}}}{g_{\rm{s}}}\left( {{\rm{1 + }}{e_{{\rm{ss}}}}} \right)\sqrt {\frac{{{\theta _{\rm{s}}}}}{\pi }} $ | (3) |
| $ {\mu _{\rm{s}}}{\rm{ = }}{\mu _{{\rm{s,col}}}}{\rm{ + }}{\mu _{{\rm{s,kin}}}} + {\mu _{{\rm{s,fr}}}} $ | (4) |
式中,
| $ {\mu _{{\rm{s}},{\rm{col}}}}{\rm{ = }}\frac{{\rm{4}}}{{\rm{5}}}\alpha _{\rm{s}}^{\rm{2}}{\rho _{\rm{s}}}{d_{\rm{s}}}{g_{\rm{s}}}\left( {1 + {e_{{\rm{ss}}}}} \right)\sqrt {\frac{{{\theta _{\rm{s}}}}}{\pi }} $ | (5) |
| $ {\mu _{{\rm{s,kin}}}}{\rm{ = }}\frac{{{\alpha _{\rm{s}}}{\rho _{\rm{s}}}{d_{\rm{s}}}\sqrt {{\theta _{\rm{s}}}\pi } }}{{6(3 - {e_{{\rm{ss}}}})}}\left[ {{\rm{1 + }}\frac{{\rm{2}}}{{\rm{5}}}\left( {1 + {e_{{\rm{ss}}}}} \right)\left( {3{e_{{\rm{ss}}}} - 1} \right){\alpha _{\rm{s}}}{g_{\rm{s}}}} \right] $ | (6) |
| $ {\mu _{{\rm{s,fr}}}} = \frac{{0.1{\alpha _{\rm{s}}}{{\left( {{\alpha _{\rm{s}}} - {\alpha _{{\rm{s,min}}}}} \right)}^2}\sin \varphi }}{{{{\left( {{\alpha _{{\rm{s,max}}}} - {\alpha _{\rm{s}}}} \right)}^5}}} $ | (7) |
式中,ds = 7.5×10-2 mm为煤粒直径,ess = 0.9为煤粒碰撞补偿系数,θs为煤粒温度,αs, max = 76.8%为煤粒极限浓度,gs为径向分布函数[17]:
| $ {g_{\rm{s}}}{\rm{ = }}{\left[ {1 - \sqrt[3]{{\frac{{{\alpha _{\rm{s}}}}}{{{\alpha _{{\rm{s,max}}}}}}}}} \right]^{ - 1}} $ | (8) |
此外,文中使用Syamlal和O’Brien基于对流化床或沉降床上的颗粒末端速度的测量得出的动量传递系数[12, 18]:
| $ {K_{{\rm{ls}}}} = \frac{3}{4} \cdot \frac{{{\alpha _{\rm{s}}}{\alpha _{\rm{l}}}{\rho _{\rm{l}}}}}{{{d_{\rm{s}}}v_{{\rm{r,s}}}^2}} \cdot {C_{\rm{D}}} \cdot \left| {{{\vec v}_{\rm{s}}} - {{\vec v}_{\rm{l}}}} \right| $ | (9) |
式中,CD为曳力函数[14]。
2.2 滤布的多孔介质模型滤布由涤纶长丝织造而成,细观几何结构复杂,难以直接建模,可将其设置为多孔介质以简化计算。ANSYS Fluent R18.1软件通过在动量方程中添加一个动量源项来模拟多孔介质对流体流动的阻碍作用。文中假设滤布为均质多孔介质,其动量源项方程为[12]:
| $ {S_i} = - \left( {\frac{\mu }{\alpha }{v_i} + \frac{1}{2} \cdot {C_2}\rho \left| v \right|{v_i}} \right) $ | (10) |
式中,Si为i方向动量源项,α为渗透率,并定义1/α为黏性阻力系数,C2为惯性阻力系数。
厢式压滤机的煤浆过滤过程为滤饼过滤,液体通过滤饼及滤布被排出滤室,固体颗粒不进入和通过滤布,因此设置液相在滤布中的黏性阻力系数和惯性阻力系数分别为5.7×1010 m-2和106 m-1[6];锁定煤粒在滤布区域厚度方向的速度vz = 0。
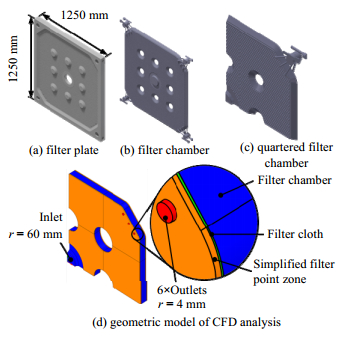
2.3 滤室的几何模型与边界条件1250型压滤机的滤板如图 1(a)所示,文中取最末端的滤室为研究对象。滤室流场模型建立过程示于图 1。在图 1(a)所示的滤板模型的基础上提取滤室几何模型,如图 1(b)所示;由于两相密度接近,模拟中忽略重力的影响并取滤室模型的1/4作为分析对象,如图 1(c);删除滤板表面支撑滤布的滤点、滤室边缘及支撑台周围的锐角等几何结构以提高计算效率,并对简化后的滤室进行适当分割,如图 1(d)所示;应用扫掠网格方法,将滤室模型划分为六面体结构化网格,合计22822个单元,71455个面,25935个节点。
|
图 1 几何模型建立示意图 Fig.1 Schematic diagram of geometric model construction |
压滤过程中由进料泵提供的进料流量Qall = 100 m3·h-1、原始煤浆浓度αcoal = 26.3%。为简化计算,假设压滤过程为煤浆在所有滤室间均匀分配的恒流过滤,则上述模型进料口流速为:
| $ {v_{{\rm{Inlet}}}}{\rm{ = }}{Q_{{\rm{all}}}}/(60 \cdot {S_{{\rm{Inlet}}}}) = 0.04\;{\rm{m}} \cdot {{\rm{s}}^{ - 1}} $ | (11) |
其他边界条件设置:模型出口定义为压力出口边界,出口压力为0;模型壁面为无滑移壁面;模型1/4分割面为对称边界。
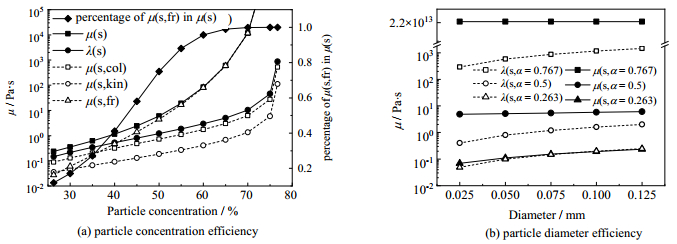
3 结果与讨论 3.1 煤浆参数对其流动性的影响为了明晰煤粒浓度、粒径等关键物理参数对煤浆流动性的影响,以式(3)~(7)为基础绘制如图 2所示的曲线图。其中,图 2(a)展示了煤粒体相黏度λs、剪切黏度μs及其组分碰撞黏度μs, col、动力黏度μs, kin、摩擦黏度μs, fr在煤粒浓度提高过程中的变化规律,并将煤粒摩擦黏度在剪切黏度中所占的比例也绘于图中。可见,随着煤浆中煤粒浓度的提高,煤粒体相黏度和剪切黏度均增加;且浓度越高,增加越快;当煤浆中的煤粒浓度接近极限浓度时,剪切黏度趋向于无穷大。此外,摩擦黏度在煤粒浓度较低时数值较小,对煤粒剪切黏度的影响甚微;在煤粒浓度达到40%后,摩擦黏度所占百分比迅速增加,逐渐成为影响煤粒剪切黏度的主要因素。因此,通过优化煤粒形状、改良煤粒表面质量,可以减小煤粒间的摩擦阻力,进而降低煤浆在高煤粒浓度状态及成饼以后的内摩擦力,减小压榨压力,降低压滤能耗和滤板载荷。
|
图 2 煤粒浓度及直径对黏度的影响 Fig.2 Effects of particle concentration and diameter on viscosity |
式(3)~(7)还说明:体相黏度λs以及剪切黏度μs中的碰撞黏度μs, col、动力黏度μs, kin两项均与煤粒直径有关,但摩擦黏度μs, fr与煤粒直径无关。如图 2(b)所示,当煤浆中的煤粒浓度较低时,减小煤粒直径可以有效减小煤粒剪切黏度μs和体相黏度λs;当浓度较高时,体相黏度λs的变化规律与低浓度时一致,而由于摩擦黏度μs, fr的影响,剪切黏度μs几乎不受粒径变化的影响。由此可见,采用减小煤粒直径的方法能减小低浓度阶段固相剪切黏度,从而提高煤浆流动性,降低能耗。
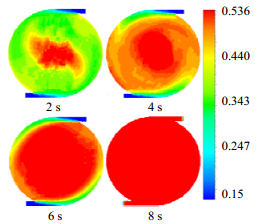
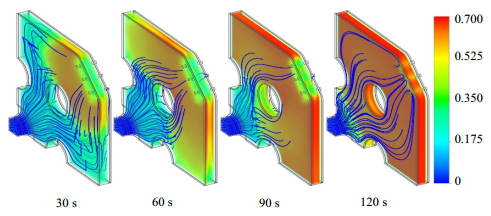
3.2 煤粒在滤室内的沉积图 3为应用CFD方法计算得到的煤粒浓度分布与液相流线图。从煤粒浓度场分布结果可见,过滤初期煤粒由于水的冲刷及自身惯性等因素,在滤布内表面远离进料口的区域积累,这与如图 4所示的文献[6]中的模拟计算得到的颗粒沉积规律及成饼趋势一致。由液相流线可知,水在煤粒成饼前沿透过滤布排出滤室,且随着煤粒不断进入滤室,滤布内表面积累的煤粒不断增多,成饼区域面积扩大、厚度增大、含固率升高,水透过滤布的位置也随之向进料口移动。
|
图 3 不同时刻煤粒浓度分布及液相流线 Fig.3 Distribution of coal particle concentration and liquid streamline at different stages |
此外,图 3显示120 s时滤室内最大煤粒浓度为70%,并未达到煤粒浓度极限,说明煤粒在沉积过程中并不能直接紧密排列达到浓度极限,而是随着压力升高被逐步压紧。在压紧过程中,由于煤粒浓度的提高,滤室内流场发生了显著的变化:
(1) 煤粒间距缩小,发生碰撞概率增加、煤粒间固体压力增大、摩擦力增大,使煤粒间作用力增大;
(2) 水穿过煤粒间隙的路程延长、流速增加,使湍流加强;
(3) 两相相对速度增加、使相间曳力增大。
流场的这些变化使其复杂程度不断提高,仿真计算所需的时间增量步不断减小。在第120 s时已减小至微秒级,继续计算至压滤完成将消耗大量资源,而此时滤室内的平均煤粒浓度已达到64.9%,与当前滤室内最大浓度接近,说明颗粒分布趋于均匀,且沉积成饼规律业已完整显现,研究目标基本达成,继续使用CFD方法进行滤室内流场模拟仿真的可行性和经济性被大幅削弱;另一方面,滤料沉积成饼后更多表现为固体,而本文所选用的颗粒间作用力的理论模型[13-18]也有其局限性,CFD仿真计算的可靠性也显著降低,所以文中仅应用CFD方法研究压滤进程的前120 s。
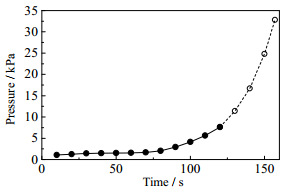
3.3 进料口压力的发展采用Velocity-Inlet为入口边界条件,边界面的压力即为维持恒流过滤所需的进料压力,其数值大小反映了料浆的流动阻力与过滤介质的过滤阻力。图 5中的实线部分即为仿真计算得到的进料压力随过滤时间的变化曲线,根据进料压力的增长速率特点,可以以第90 s为界将压滤过程分为两个阶段。在第90 s之前,进料压力增长缓慢,这是因为虽然成饼区域在不断扩大但剩余未成饼区域的滤布面积仍能满足水的排出,此时煤浆流动阻力较小,而过滤阻力主要来自滤布对水的阻碍,所以进料压力较小且增长较缓慢。在90 s之后,滤室内煤粒浓度增加,颗粒间作用力逐渐增大,流动阻力大幅提高,而且此时滤饼已经完全覆盖滤布内表面并替代滤布成为主要的过滤介质,而由于其渗透率远小于滤布、厚度远大于滤布且在不断增加,水透过过滤介质的阻力显著提高,进而使得持续进料所需的压力提高。至120 s时进料压力为8.61×103 Pa。
|
图 5 进料口压力-时间关系曲线 Fig.5 Profile of inlet pressure as a function of time |
将计算所得进料压力-时间关系曲线拟合,可得下式:
| $ P = 1084 + 45.76 \cdot {\rm{exp}}\left( {t/24} \right) $ | (12) |
式中,P为进料压力,t为时间。
由此预测进料压力将以更快的速度增长,直至第157 s滤室内全部达到极限浓度,此时进料压力为3.28×104 Pa,如图 5中虚线段所示。
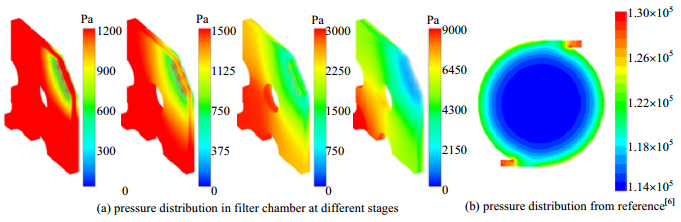
3.4 滤室内压力的分布在压滤过程中滤室内压力的时间演变规律、空间分布特点示于图 6(a)。其中,进料口始终为滤室内压力最大的区域,其压力随时间不断增大;出水口周围压力最小,但在压滤进程中也不断增大。滤室内每一时刻均存在由进料口到出水口的压降,该空间分布规律及时间演化趋势与文献[5-6]基本一致,如图 6(b)。此外,在靠近进料口的区域压力呈均匀分布,不存在明显的压力梯度,说明该区域内煤浆具有较好的流动性,流变特性仍满足牛顿线性流变方程;而在靠近出水口的区域内则存在明显的压力梯度,这是由于煤粒的沉积及颗粒间作用力的显著提高,煤浆的流变特性不再符合牛顿线性流变方程,开始出现拟塑性并转变为宾汉流体甚至固体,煤粒间及煤粒与滤布间的黏着力、摩擦力等相互作用的产生和增大使该区域出现明显的压力梯度。结合图 3可以分析得到压力梯度与煤粒浓度的分布规律:当区域煤粒浓度达到一定阈值时,才会出现压力梯度,即:煤浆的流变特性转变与煤粒浓度相关并存在阈值。
|
图 6 滤室内压力分布云图 Fig.6 Pressure distribution in filter chamber |
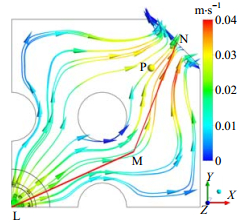
为了进一步研究滤室内压力分布与煤粒浓度分布间的关系,参考滤室中间截面里的液相流线,建立如图 7所示的折线
|
图 7 路径 |
|
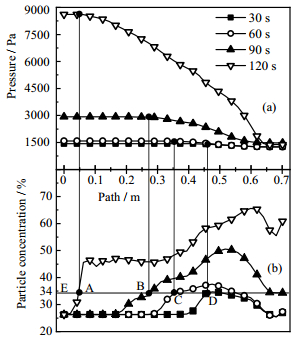
图 8 沿路径 |
图 8(a)为不同时刻路径
图 8(b)为不同时刻路径
结合图 2(a)可见,当煤粒浓度为34%时,体相黏度λs及碰撞黏度μs, col为影响颗粒间作用力主要因素,减小煤粒直径可降低该浓度时的颗粒间作用力,进而推迟煤浆的流变特性转变,提高煤浆在滤室内的流动效率。
4 结论与展望(1) 煤粒间的碰撞及黏着力是压滤前期煤浆流动阻力的主要来源,减小煤粒直径可有效提高该阶段煤浆流动性,并推迟煤浆的拟塑性转变,提高煤浆流动效率,降低泵料阶段压力。
(2) 煤粒间摩擦为压滤后期滤饼压榨阻力的主要来源,优化煤粒形状及表面质量可降低煤粒间摩擦,降低滤饼压榨过程的能耗和滤板负载。
(3) 压滤过程中滤室内各处压力均不断升高,且入口处压升幅度远大于出口处,因此可在滤板强度优化设计中适当加强进料口附近强度并向出口逐步减弱,以提高滤板强度和使用寿命、减少滤板用料。
在下一步研究中,将建立含有数十个滤室的完整压滤机滤室几何模型,结合整机精煤压滤脱水实验,研究煤浆在滤室间的分配规律以及压力、速度等在滤室堆叠方向上的分布特点,并应用用户定义函数定义进料边界,进而分析泵的扬程与流量之间的关系。在理论模型及研究方法上将使用计算流体动力学与离散单元法耦合的方式,更加准确可靠地模拟压滤过程中煤浆的流动形态及滤料的沉积成饼规律,并以此为基础分析滤板使役状态、优化设计滤板结构。
符号说明:
| CD | — 曳力函数 | v | — 流速,m·s-1 |
| C2 | — 惯性阻力系数,m-1 | vInlet | — 入口边界速度,m·s-1 |
| D | — 黏性阻力系数,m-2 | αcoal | — 原始煤浆煤粒浓度 |
| ds | — 颗粒直径,m | αs | — 煤粒浓度 |
| ess | — 颗粒碰撞补偿系数 | αs, max | — 煤粒极限浓度 |
| — 固相浮力,Pa | αs, min | — 煤粒最小浓度 | |
| — 固相体积力,Pa | α | — 多孔介质渗透率,m2 | |
| — 固相湍流耗散力,Pa | θs | — 颗粒温度,K | |
| — 固相虚拟质量力,Pa | λ | — 颗粒体相黏度,Pa·s | |
| — 重力加速度,m·s-2 | μ | — 黏度,Pa·s | |
| gs | — 径向分布函数 | μs | — 颗粒剪切黏度,Pa·s |
| — 单位张量 | μs, col | — 颗粒碰撞黏度,Pa·s | |
| Ksl | — 固-液相间动量传递系数 | μs, fr | — 颗粒摩擦黏度,Pa·s |
| P | — 进料口压力,Pa | μs, kin | — 颗粒动力黏度,Pa·s |
| p | — 压力,Pa | ρ | — 密度,kg·m-3 |
| ps | — 固体压力,Pa | — 固相应力张量,Pa | |
| Qall | — 压滤机进料流量,m3·s-1 | φ | — 压力角,° |
| Res | — 固相雷诺数 | 下标 | |
| S | — 动量源项 | s | — 颗粒相 |
| SInlet | — 滤板进料口面积,m2 | l | — 液相 |
| t | — 时间,s | i | — 第i坐标方向 |
| [1] | ZHANG De-you(张德友), ZHOU Jin(周进). Brief analysis on the present situation and development prospect of the filter press industry(中国压滤机行业现状和发展前景浅析)[J]. Journal of Filtration & Separation(过滤与分离), 2010, 20(2): 39-42. DOI:10.3969/j.issn.1005-8265.2010.02.013. |
| [2] | TANG Cun-ben(唐存本). The formula of the limit stress of bingham fluid with sand(含沙水流的宾汉极限应力的计算公式)[J]. Journal of Sediment Research(泥沙研究), 1981(2): 62-67. |
| [3] | ZHAN Yi-zheng(詹义正), WU Wei-min(吴伟民), WANG Dan(王丹). The study of the yield stress of slurry(浆体极限切应力的研究)[J]. Journal of Basic Science and Engineering(应用基础与工程科学学报), 1996, 4(1): 85-93. |
| [4] | CHE De-fu(车得福), LI Hui-xiong(李会雄). Multiphase flow and its application(多相流及其应用)[M].Xi'an(西安): Xi'an Jiaotong University Press(西安交通大学出版社), 2007. |
| [5] | TAN Wei(谭蔚), GENG Ya-mei(耿亚梅), FENG Guo-hong(冯国红), et al. Flow norphology within filter chamber of the new dynamic cross-flow plate and frame filter press(新型动态扫流板框压滤机滤室流动形态研究)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报), 2013, 27(6): 931-936. DOI:10.3969/j.issn.1003-9015.2013.06.003. |
| [6] | GENG Ya-mei (耿亚梅). Study on the filtration process of the new dynamic cross-flow plate and frame filter press (新型动态扫流板框压滤机过滤过程研究)[D]. Tianjin (天津): Tianjin University (天津大学), 2013. http://cdmd.cnki.com.cn/Article/CDMD-10056-1014036829.htm |
| [7] | DENG Ling (邓玲). Filter characteristics research on deep dehydration of sludge in van nembrane filter press (厢式隔膜压滤机污泥深度脱水过滤特性研究)[D]. Changsha (长沙): Central South University (中南大学), 2014. http://cdmd.cnki.com.cn/Article/CDMD-10533-1014408510.htm |
| [8] | GUO Nian-qin(郭年琴), QIAO Bao-meng(乔保蒙), LIN Tong(林通). Numerical modeling and simulation on chamber filter press filtration process(厢式压滤机过滤过程数值模拟与仿真)[J]. Metal Mine(金属矿山), 2016, 45(5): 144-148. DOI:10.3969/j.issn.1001-1250.2016.05.030. |
| [9] | QIAO Bao-meng (乔保蒙). Structure optimization and filtration process simulation of XAY160/1250-U type filter press (XAY160/1250-U型压滤机结构优化及过滤过程仿真)[D]. Ganzhou (赣州): Jiangxi University of Science and Technology (江西理工大学), 2016. http://cdmd.cnki.com.cn/Article/CDMD-10407-1016244834.htm |
| [10] | QIU Qin-mu (邱勤木). The research of pressing filter CFD model and optimization of dewatering process (压滤CFD模型及脱水过程的优化研究)[D]. Ganzhou (赣州): Jiangxi University of Science and Technology (江西理工大学), 2015. http://cdmd.cnki.com.cn/Article/CDMD-10407-1015424970.htm |
| [11] | Du W, Bao X, Xu J, et al. Computational fluid dynamics (CFD) modeling of spouted bed:assessment of drag coefficient correlations[J]. Chemical Engineering Science, 2006, 61(5): 1401-1420. DOI:10.1016/j.ces.2005.08.013. |
| [12] | ANSYS Fluent Theory Guide[Z]: Release 18.1. Canonsburg, PA: ANSYS Inc. 2017. |
| [13] | Syamlal M, Rogers W, O'Brien T J. MFIX documentation theory guide[Z]. West Virginia: Morgantown Energy Technology Center. 1993: 10-39. |
| [14] | Johnson P C, Jackson R. Frictional-collisional constitutive relations for granular materials, with application to plane shearing[J]. Journal of Fluid Mechanics, 2006, 176: 67-93. |
| [15] | Ocone R, Sundaresan S, Jackson R. Gas-particle flow in a duct of arbitrary inclination with particle—particle interactions[J]. AIChE Journal, 1993, 39(8): 1261-1271. DOI:10.1002/(ISSN)1547-5905. |
| [16] | Lun C K K, Savage S B, Jeffrey D J, et al. Kinetic theories for granular flow:inelastic particles in Couette flow and slightly inelastic particles in a general flow field[J]. Journal of Fluid Mechanics, 1984, 140: 223-256. DOI:10.1017/S0022112084000586. |
| [17] | Ogawa S, Umemura A, Oshima N. On the equations of fully fluidized granular materials[J]. Zeitschrift Für Angewandte Mathematik Und Physik Zamp, 1980, 31(4): 483-493. DOI:10.1007/BF01590859. |
| [18] | Syamlal M, O'Brien T J. Computer simulation of bubbles in a fluidized bed[J]. AIChE Symposium Series, 1989, 85(1): 22-31. |