2. 浙江大学衢州研究院,浙江 衢州 324000
2. Institute of Zhejiang University-Quzhou, Quzhou 324000, China
气体分布器孔口初始气泡的生成对鼓泡塔流体力学有重要影响,生成气泡的大小与形状决定着气泡的浮升速度和传质面积,并由此确定宏观流动特性如气含率、两相流型、速度分布、混合与传质速率等。工业鼓泡塔多采用高温高压操作条件,涉及的又往往是黏性液体,如重油加氢裂化[1]、煤直接液化[2]、液相费托合成[3]。因此,研究高温高压下黏性流体中气泡生成过程具有重要的理论与应用价值。文献中以往针对黏性体系的气泡生成研究多为常温常压条件。DAVIDSON [4]实验考察了高黏度液体(0.5~1.04Pa·s)中的气泡生成,指出黏度越大,气泡生成时间越长,气泡直径越大。SIEMES [5]认为在低黏度液体中黏度对气泡直径无影响,而在高黏液体中低气速下气泡直径随黏度增加而增加。RAMAKRISHNAN[6]同样提出低气速低黏度下黏度对气泡直径影响较小。归纳起来,有关液体黏性对气泡直径的影响文献中存在着不一致的结果:1)气泡直径随液体黏度增加而显著增加[7-9];2)气泡直径与黏度无关[10-11]或只有微弱关系[12]。许多文献考虑了压力和温度对气泡生成的影响,但多针对低黏度的空气-水体系[10, 13-15]。一般认为压力增加,气泡直径减小。温度的影响多归结于对物性的改变[16],如液体黏度、表面张力、饱和蒸气压。WEN[16]研究空气-水体系发现,在温度283到308 K时,气泡直径随温度升高而增大,在308到363 K时则随着温度升高而降低。针对黏性液体考虑压力与温度对孔口气泡生成过程的文献极少。LUO[17]和YANG[18-19]以导热油(常温常压下黏度为0.023 Pa·s)为液体体系研究时发现,压力对气泡生成影响很小,其解释是随着压力增加,气体动量增加,同时液体惯性力、巴塞特力增加,表面张力减小,气泡受力互相抵消,从而压力影响可以忽略。YOO[20]以13.7%甘油水溶液为液体体系,研究压力对气泡生成影响,指出气泡直径随着压力增加而减小。
通过文献检索可以发现,针对黏性流体中压力温度对孔口气泡生成过程的影响研究还很少,缺乏清楚的认识和重要的实验数据,而许多工业气液反应过程都在高温高压和黏性液体条件下操作,因此有必要建立专门的实验手段观察这种苛刻条件下的气泡生成过程,获取相关的信息或基础数据。有鉴于此,本文专门设计加工了一套带视窗的高温高压鼓泡塔实验装置,采用高速摄像法观察孔口气泡生成过程,测定气泡尺寸、形状、生成时间,考察压力、温度、孔径的影响,并归纳出定量关系式,为进一步的流动模拟和工业应用提供依据。
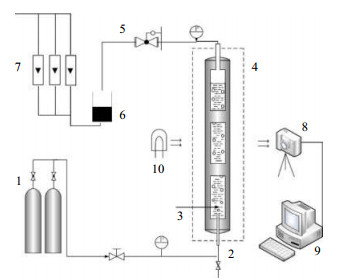
2 实验设备与测试方法实验装置包括两部分:鼓泡塔与图像采集系统,如图 1所示。实验流程由气体钢瓶1、鼓泡塔2、恒温箱4、背压阀5、气液分离装置6组成。鼓泡塔采用316L不锈钢加工而成,塔径50 mm、塔高600 mm,放置在气体恒温箱中。在鼓泡塔的前后两侧各安装三块20 mm×100 mm可视化视窗3,视窗采用耐高压高温材料(硅铝酸盐玻璃)制成。塔温由恒温箱控制,压力通过背压阀调节。该装置设计压力8 MPa、设计温度573 K。气体由气体钢瓶经过预热装置后通过单孔喷嘴进入鼓泡塔,经过背压阀后,再通过转子流量计7。初始液位距离孔口45 cm,实验气体为氮气,液体为硅油;气体进料管孔口直径do分别为1.12和2.5 mm;塔内操作压力为0~3 MPa,塔内操作温度为283~473 K;孔口气速范围为0~1 500 cm·s-1。硅油在不同温度下的黏度采用德国HAAKE公司流变仪(HAAKE RS6000)测量,气液表面张力通过德国Dataphysics公司的视频接触角度装置(OCA 20)测量。物性分别测量三次取平均,在95%的置信度下,黏度与表面张力的不确定度分别为2.0%和1.0%。不同温度下液体性质如表 1所示。
|
图 1 实验装置简图 Fig.1 Schematic diagram of the experimental setup 1. gas cylinders 2. bubble column 3. visual window 4. thermostat 5. back-pressure valve 6. demister 7. flow meters 8. high-speed camera 9. computer 10. light |
|
|
表 1 不同温度下硅油液体性质 Table 1 Properties of silicone oil at different temperatures |
气泡形状通过高速摄像机8 (CUBE 7)拍摄,拍摄频率500 fps,分辨率512×1 738 (在1mm2区域内的分辨率近似为19×19)。进气管外径(3 mm)则作为图像分辨率的校准尺寸。
气泡当量直径d为
| $d = \sqrt[3]{{\frac{{6V}}{\pi }}}$ | (1) |
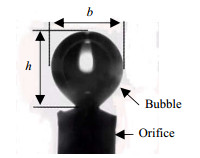
式中,V为气泡体积,根据高速摄像机拍摄的图像、利用MATLAB软件进行处理和计算得到。处理方法如图 2所示,沿纵轴方向将气泡生长高度h平分为N段,每段半径为Rk。由于气泡形状近似为轴对称旋转体,故气泡的体积等于N个圆柱体的体积之和[21],计算式如下:
|
图 2 孔口气泡形状 Fig.2 Bubble shape at the orifice |
| $V = \sum\limits_{k = {k_b}}^{{k_t}} {\pi R_k^2\Delta z} $ | (2) |
气泡的纵横比E由下式计算。
| $E = \frac{h}{b}$ | (3) |
式中,b为气泡的横向长度,m。
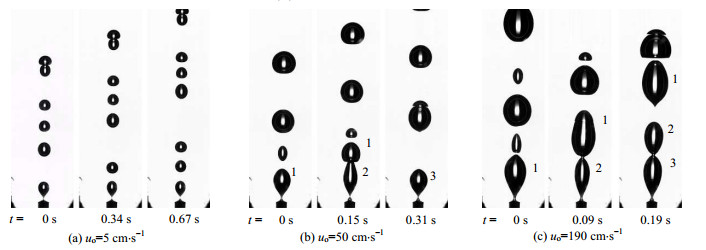
3 结果与讨论 3.1 黏性液体中的气泡生成模式为了对黏性液体中气泡生成有直观上的认识,图 3给出了常温常压时不同孔口气速uo下气泡的生成图像。低气速时,如图 3(a)所示,气泡生成频率不一,气泡直径分布宽。ILIADIS[22]亦发现低气速时,气泡的生成为周期性的连串产生,即多个气泡从孔口快速产生后,间歇一段时间,又有多个气泡快速从孔口产生。作者又同时指出,气泡脱离后,难以重新建立稳定的气液面,从而导致这种现象发生。随气速增加,如图 3(b)所示,气泡生成模式变为双气泡模式,即气泡2在气泡1的尾涡作用下变得狭长,生成时间变短,脱离孔口后与气泡1发生聚并。高气速时,如图 3(c)所示,气泡2在孔口处就与气泡1发生聚并,从而产生一大一小的气泡对。

|
图 3 常温常压时不同孔口气速下气泡的生成图像 Fig.3 Bubble formation at different orifice flow rates under ambient conditions |
图 4给出了常温高压时不同孔口气速下气泡的生成图像。气速较低时,如图 4(a)所示,气泡均匀产生,气泡大小一致。随着气速增加,如图 4(b)所示,变为双气泡模式,对比常压情况,出现双气泡模式时的临界气体速度减小。高气速时,如图 4(c)所示,则出现气泡连串产生现象,气泡相互连接在一起。
|
图 4 常温高压时不同孔口气速下气泡的生成图像 Fig.4 Bubble formation at different orifice flow rates under ambient temperature and high pressures |
在高温高压下,气泡生成亦是相同的变化趋势,在中等气速下一大一小的气泡成对产生。
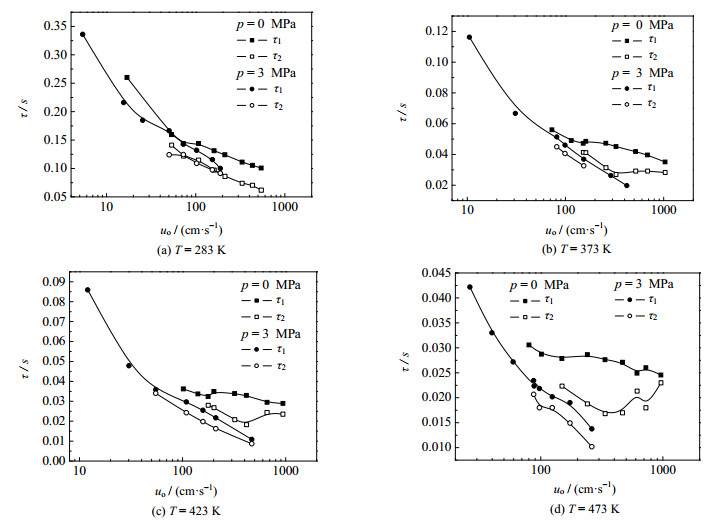
对气泡生成图像分析可知,气速较高时,受黏性力作用,气泡在孔口生成时所受阻力较大,导致高黏液体中气泡直径比低黏液体更大,且气泡脱离孔口后浮升速度较小,新气泡生成时与已生成大气泡的距离较小,新气泡受已生成大气泡强烈的尾涡卷吸,气泡变得狭长,快速从孔口脱离。气泡直径呈现一大一小周期性变化,此时气泡生成时间亦呈现大小周期性变化,气泡生成时间即为气泡频率的倒数。此时大小气泡生成频率相同。图 5给出了不同温度压力下气泡生成时间τ随孔口气速的变化。由图可见,气泡生成时间随气速增加逐渐减小。相同气速下随着压力增加,气泡生成时间减小。低气速时,为单气泡生成模式;随气速增加,变为双气泡模式,小气泡的生成时间τ2小于相同气速下大气泡的生成时间τ1。从图上还可以看出,常压低温低速时气泡生成时间随气速迅速减小,高气速时,减小趋势变缓。高温时,气泡生成时间在高气速下趋于稳定,气速影响较小。
|
图 5 不同温度压力下气泡生成时间随气速变化 Fig.5 Bubble formation times at different flow rates under different temperatures and pressures (do=1.12 mm) |
图 6给出了不同温度压力下孔口生成的气泡直径与孔口气速的关系。由于气速较高时,双气泡模式中小气泡直径难以直接测量,文中气泡直径值都为大气泡的直径。如图所示,气泡的直径随气速增加而增大。在所有温度下,压力增加均导致气泡直径减小,但其影响随着温度增加而增大,或者说,高温下加压会导致气泡显著减小(见图 6(b)~(c)),而常温下加压效果不明显(见图 6(a))。同时,气速增大也会使压力效应趋于显著。LIN[23]指出,对于高黏度体系,温度低时,加压会显著增加液体黏度,其效应随着温度增加而减小。同时压力增加,降低了表面张力,增加了气体动量力,从而抵消了压力的黏度效应,导致低温与高温下压力的影响显著性不同。
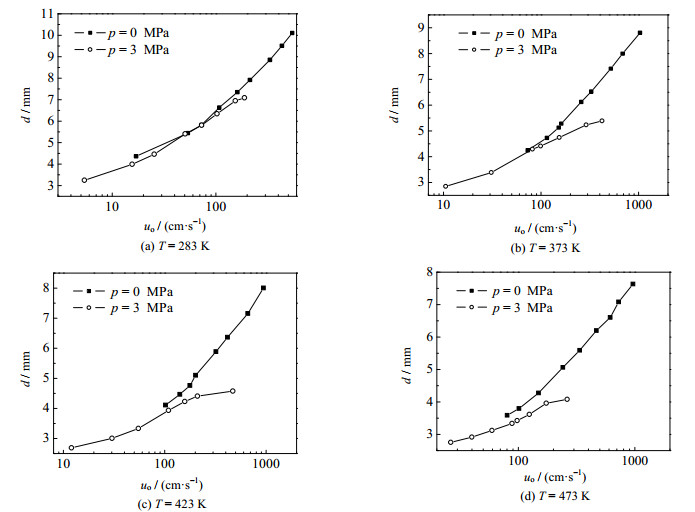
|
图 6 压力对气泡直径的影响 Fig.6 Effects of pressure on bubble diameter (do=1.12 mm) |
加压不仅会改变气泡的直径,同时也会使气泡的形状发生变化。图 7给出了常温时不同压力下,孔口气速为100 cm·s-1时的大气泡生成图像。由图可见,气泡生成经历了膨胀与脱离两个阶段,该气速下膨胀阶段占主要部分,如图 7(b),气泡在0.11 s左右开始脱离。随着压力增加,液体黏度增加,气泡生成时间变化较小,在0和1 MPa时都经历了0.142 s;图 8则给出了高温(473 K)时不同压力下的大气泡的生成图像。由图可以发现,高温下加压使气泡生成时间、气泡直径显著减小。图 9给出了常温下大气泡的纵横比随压力的变化。由图可以看出,气泡纵横比随压力增加而增大,即加压使气泡变长;图 10则给出了高温下大气泡的纵横比随压力的变化。由图可见,压力增加,纵横比显著增加。说明压力对气泡大小与气泡形状的影响是一致的,即低温时影响小,高温时影响大。

|
图 7 常温时不同压力下的大气泡生成图像 Fig.7 Big bubble formation at different pressures under ambient temperature (do=1.12 mm, uo=100 cm·s-1) |

|
图 8 高温时不同压力时的大气泡生成图像 Fig.8 Big bubble formation at different pressures under high temperature (do= 1.12 mm, uo=100 cm·s-1) t / s |
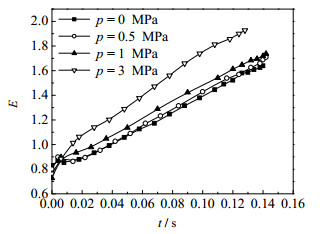
|
图 9 常温下大气泡纵横比随压力的变化 Fig.9 Big bubble aspect ratios as a function of pressure under ambient temperature (do= 1.12 mm, uo=100 cm·s-1)t / s |
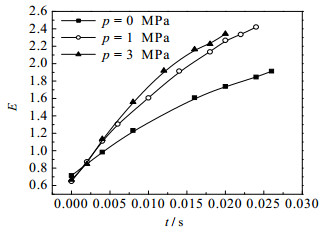
|
图 10 高温下大气泡纵横比随压力的变化 Fig.10 Big bubble aspect ratios as a function of pressure under high temperature (do= 1.12 mm, uo=100 cm·s-1) |
图 11给出了不同压力时大气泡的直径随温度的变化。可以发现随着温度增加,相同气速下气泡直径迅速减小,其原因是温度增加,液体黏度和表面张力均减小,使气泡生成时的阻力减小,导致气泡直径减小。图 12给出了不同温度下大气泡的生成图像,可以直观的发现随温度增加气泡直径明显减小。
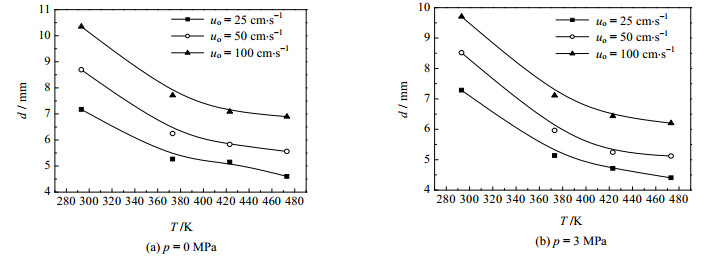
|
图 11 温度对大气泡的直径的影响 Fig.11 Effects of temperature on big bubble diameter (do=2.5 mm) |

|
图 12 不同温度下大气泡生成图像 Fig.12 Big bubble formation at different temperatures (p =3 MPa, do=2.5 mm, uo=25 cm·s-1) |
图 13给出了温度对大气泡生成时间的影响。由图可见,随着温度增加,液体黏度、表面张力减小,气泡生成所受阻力减小,气泡生成时间快速减小。图 12给出了不同温度下气泡生成的图像。对于常温情况,如图 12(a)所示,气泡在0.118s开始进入脱离阶段,0.164s从孔口脱离;而对于高温情况,如图 12(c)所示,气泡在0.026s时就开始进入脱离阶段,0.036s就从孔口脱离。从图上还可以看出气泡脱离孔口时,在孔口处仍存在一个小气泡,然后小气泡在孔口膨胀脱离,且随着温度增加,气泡脱离时小气泡体积变小。CORCHERO[24]研究恒速流下气泡生成时,亦发现小气泡存在的现象。
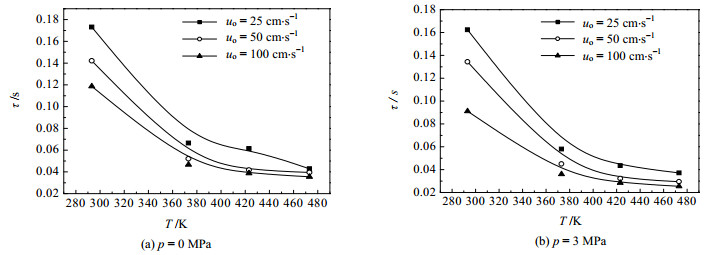
|
图 13 温度对大气泡生成时间的影响 Fig.13 Effects of temperature on big bubble formation time (do=2.5 mm) |
以往文献中曾经提出过一些气泡直径的关联式,但都是基于常温常压实验归纳得出的。为检验其在高温高压下的适用性,分别对不同关联式的计算值与本文测量值进行了比较。图 14给出了不同模型下气泡直径计算值dcal与本文测量值d的比值,其中横坐标Weg (=ρguo2do/σ)是气体韦伯数,表征气体惯性力与表面张力的比值。常压下,如图 14(a)所示,GADDIS [25]、JAMIALAHMADI[26]以及KUMAR模型[10]计算值与本文实验符合较好,DAVISDON[8]与WANG模型[27]计算值偏低,BHAVARAJU模型[28]计算值则偏高。3 MPa时,如图 14(b)所示,GADDIS、JAMIALAHMADI以及KUMAR模型计算值在低温时符合较好,高温时偏大。这些模型都没有考虑到高温高压下气体动量力在气泡脱离方面的贡献,从而导致其气泡直径计算值偏大。DAVISDON与WANG模型计算值远低于本文实验值,BHAVARAJU模型则偏高。
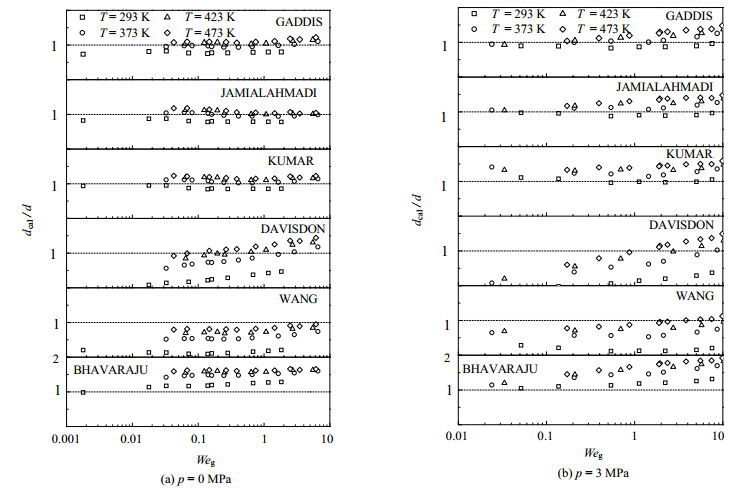
|
图 14 不同模型下气泡直径计算值与本文测量值比值 Fig.14 Comparison of bubble diameter calculated from different models with experimental data (do=1.12 mm) |
压力增加显著增大了气体动量力,使得气泡生成时间减小,直径减小,而以往的关联式低估了这方面的影响,需要根据新的实验数据予以修正。基于GADDIS模型[25]具有较好的预测性,本文考虑以此为基础进行修正。GADDIS模型如下。
| $d = {\left( {{S^{4/3}} + L + {W^{4/5}}} \right)^{1/4}}$ | (4) |
式中,S、L、W分别代表表面张力、黏性力、惯性力的贡献,计算式如下。
| $ S = \frac{{6{d_{\rm o}}\sigma }}{{({\rho _{\rm l}} - {\rho _{\rm{g}}})g}} $ | (5) |
| $L = \frac{{81{\mu _{\rm l}}Q}}{{\pi ({\rho _{\rm l}} - {\rho _{\rm{g}}})g}}$ | (6) |
| $W = \left( {\frac{{135}}{{4{\pi ^2}}} + \frac{{27}}{{{\pi ^2}}}\frac{{{\rho _g}}}{{{\rho _{\rm l}}}}} \right)\frac{{{\rho _{\rm l}}{Q^2}}}{{({\rho _{\rm l}} - {\rho _{\rm g}})g}}$ | (7) |
为考虑高温高压对气泡生成作用,对该模型进行修正,增加一项气体惯性力的贡献项,用Weg表征,式(4)修正如下。
| $d = {\left[ {\left( {1 - aW{e_{\rm{g}}}^b} \right){S^{4/3}} + L + {W^{4/5}}} \right]^{1/4}}$ | (8) |
经过非线性拟合得到系数a=0.80,b=1.47。图 15展示了气泡直径的计算值和测量值对比,相对误差绝大多数都在±15%以内,平均误差值为5.5%,表明拟合效果较好。图 15同时展示了气泡直径的式(8)计算值与以往文献中常温常压下的测量值对比[4, 6, 25-26, 29],共对比了607组数据,相对误差绝大多数都在±15%以内,平均误差值为5.0%。说明式(8)不仅适用于高温高压黏性液体,也适用于常温常压低黏液体。
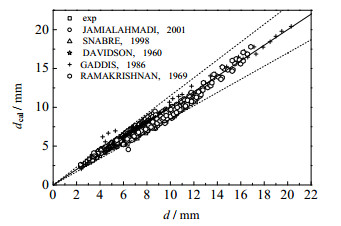
|
图 15 气泡直径的式(8)计算值与实验值比较 Fig.15 Comparison of measured bubble diameters with values calculated from Equation (8) |
本文采用特定的高温高压实验装置,观察不同条件下氮气-硅油体系孔口气泡的生成过程,测定了气泡直径、气泡生成时间、气泡纵横比等参数,考察了温度(283~473 K)、压力(0~3 MPa)、孔径(1.12和2.5 mm)的影响,获得大量直观的气泡生成图像和基础实验数据,得到以下结论:
(1) 低气速时,气泡生成为单气泡模式;随着气速增加,由于受气泡尾涡卷吸作用,在黏性流体中存在明显的一大一小的双气泡生成模式,这是黏性液体中气泡生成区别于低黏液体的一个特征。
(2) 压力对气泡直径的影响随温度而变化:低温时,压力在相同气速下对气泡直径影响较小。高温时,随压力增加,气泡直径明显减小。压力的增加同时对气泡形状产生影响:压力增加,气泡纵横比明显增加。
(3) 温度的影响归因于对气液性质的改变。温度增加,液体的黏度和表面张力减小,气泡直径减小。低温下,气泡脱离时间间隔随气速增加而减小;高温时,气泡脱离时间间隔在高速时趋于定值,气速影响较小。
(4) 通过与以往文献中在常温常压操作条件下提出的气泡直径关联式进行对比发现,以往关联式在高压下低估了气体动量力的贡献使其计算值偏低。基于新的实验数据修正了GADDIS提出的关联式,提出了适用于高温高压条件下气泡直径的估算式如下:
符号说明:
|
|
| [1] |
CALDERÓN C J, ANCHEYTA J. Modeling of slurry-phase reactors for hydrocracking of heavy oils[J]. Energy & Fuels, 2016, 30(4): 2525-2543. |
| [2] |
张玉卓. 中国煤炭液化技术发展前景[J]. 煤炭科学技术, 2006(1): 19-22. ZHANG Y Z. Development outlook of China coal liquefaction technology[J]. Coal Science and Technology, 2006(1): 19-22. DOI:10.3969/j.issn.0253-2336.2006.01.006 |
| [3] |
BASHA O M, SEHABIAGUE L, ABDEL-WAHAB A, et al. Fischer-Tropsch synthesis in slurry bubble column reactors: Experimental investigations and modeling-a review[J]. International Journal of Chemical Reactor Engineering, 2015, 13(3): 201-288. DOI:10.1515/ijcre-2014-0146 |
| [4] |
DAVIDSON J. Bubble formation at an orifice in a viscous liquid[J]. Transaction of Institute of Chemical Engineering, 1960, 38: 144-154. |
| [5] |
SIEMES W, KAUFFMANN J. Die periodische entstehung von gasblasen an dusen[J]. Chemical Engineering Science, 1956, 5(3): 127-139. DOI:10.1016/0009-2509(56)80028-6 |
| [6] |
RAMAKRISHNAN S, KUMAR R, KULOOR N R. Studies in bubble formation-I bubble formation under constant flow conditions[J]. Chemical Engineering Science, 1969, 24(4): 731-747. DOI:10.1016/0009-2509(69)80065-5 |
| [7] |
TERASAKA K, TSUGE H. Bubble formation at a single orifice in highly viscous liquids[J]. Journal of Chemical Engineering of Japan, 1990, 23(2): 160-165. DOI:10.1252/jcej.23.160 |
| [8] |
ZAHEDI P, SALEH R, MORENO-ATANASIO R, et al. Influence of fluid properties on bubble formation, detachment, rising and collapse; Investigation using volume of fluid method[J]. Korean Journal of Chemical Engineering, 2014, 31(8): 1349-1361. DOI:10.1007/s11814-014-0063-x |
| [9] |
SATTARI A, HANAFIZADEH P. Bubble formation on submerged micrometer-sized nozzles in polymer solutions: An experimental investigation[J]. Colloids and Surfaces A: Physicochemical and Engineering Aspects, 2019, 564: 10-22. |
| [10] |
KUMAR R, KULOOR N. The formation of bubbles and drops[M]. Bangalore: Academic Press, 1970: 255-368.
|
| [11] |
BENZING R J, MYERS J E. Low frequency bubble formation at horizontal circular orifices[J]. Industrial & Engineering Chemistry, 1955, 47(10): 2087-2090. |
| [12] |
DATTA R, NAPIER D, NEWITT D. The properties and behaviour of gas bubbles formed at circular orifices[C]// Chemistry & Industry. 14 Belgrave Square, London Sw1x 8PS, England: Soc Chemical Industry, 1950(9): 168-168.
|
| [13] |
IDOGAWA K, IKEDA K, FUKUDA T, et al. Formation and flow of gas bubbles in a pressurized bubble column with a single orifice or nozzle gas distributor[J]. Chemical Engineering Communications, 1987, 59(1-6): 201-212. DOI:10.1080/00986448708911995 |
| [14] |
TSUGE H, NAKAJIMA Y, TERASAKA K. Behavior of bubbles formed from a submerged orifice under high system pressure[J]. Chemical Engineering Science, 1992, 47(13/14): 3273-3280. |
| [15] |
WILKINSON P M, VANDIERENDONCK L L. A theoretical-model for the Influence of gas properties and pressure on single-bubble formation at an orifice[J]. Chemical Engineering Science, 1994, 49(9): 1429-1438. DOI:10.1016/0009-2509(93)E0024-7 |
| [16] |
WEN J M, GU H F, SUN Q N, et al. Bubble formation characteristic of submerged single-hole orifice in inorganic solution[C]// 2017 25th International Conference on Nuclear Engineering. American Society of Mechanical Engineers Digital Collection, 2017.
|
| [17] |
LUO X, YANG G, LEE D, et al. Single bubble formation in high pressure liquid-solid suspensions[J]. Powder technology, 1998, 100(2/3): 103-112. |
| [18] |
YANG G, LUO X, LAU R, et al. Bubble formation in high-pressure liquid-solid suspensions with plenum pressure fluctuation[J]. AIChE Journal, 2000, 46(11): 2162-2174. DOI:10.1002/aic.690461109 |
| [19] |
YANG G. Bubble formation dynamics and transport phenomena in high pressure bubble columns and slurry bubble columns[D]. Columbus: The Ohio State University, 2001.
|
| [20] |
YOO D H, TSUGE H, TERASAKA K, et al. Behavior of bubble formation in suspended solution for an elevated pressure system[J]. Chemical Engineering Science, 1997, 52(21/22): 3701-3707. |
| [21] |
AOYAMA S, HAYASHI K, HOSOKAWA S, et al. Shapes of ellipsoidal bubbles in infinite stagnant liquids[J]. International Journal of Multiphase Flow, 2016, 79: 23-30. DOI:10.1016/j.ijmultiphaseflow.2015.10.003 |
| [22] |
ILIADIS P, DOUPTSOGLOU V, STAMATOUDIS M. Effect of orifice submergence on bubble formation[J]. Chemical Engineering & Technology, 2000, 23(4): 341-345. |
| [23] |
LIN T J, TSUCHIYA K, FAN L S. Bubble flow characteristics in bubble columns at elevated pressure and temperature[J]. AIChE journal, 1998, 44(3): 545-560. DOI:10.1002/aic.690440306 |
| [24] |
CORCHERO G, MONTA S J L, CORCHERO T LLEZ J. Effect of flow rate conditions on bubble formation[J]. International Journal of Heat and Mass Transfer, 2012, 55(19/20): 5044-5052. |
| [25] |
GADDIS E S, VOGELPOHL A. Bubble Formation in quiescent liquids under constant flow conditions[J]. Chemical Engineering Science, 1986, 41(1): 97-105. DOI:10.1016/0009-2509(86)85202-2 |
| [26] |
JAMIALAHMADI M, ZEHTABAN M R, M LLER-STEINHAGEN H, et al. Study of bubble formation under constant flow conditions[J]. Chemical Engineering Research and Design, 2001, 79(5): 523-532. DOI:10.1205/02638760152424299 |
| [27] |
HONGYI W, FENG D, YUCHEN B, et al. Improved correlation for the volume of bubble formed in air-water system[J]. Chinese Journal of Chemical Engineering, 2011, 19(3): 529-532. DOI:10.1016/S1004-9541(11)60017-7 |
| [28] |
KANTARCI N, BORAK F, ULGEN K O. Bubble column reactors[J]. Process Biochemistry, 2005, 40(7): 2263-2283. DOI:10.1016/j.procbio.2004.10.004 |
| [29] |
SNABRE P, MAGNIFOTCHAM F. I. Formation and rise of a bubble stream in a viscous liquid[J]. The European Physical Journal B-Condensed Matter and Complex Systems, 1998, 4(3): 369-377.
|




