2. 杭州制氧机集团股份有限公司, 浙江 杭州 311305;
3. 南京钢铁联合有限公司气体供应公司制氧厂, 江苏 南京 210035
2. Hangzhou Oxygen Plant Group Company Limited, Hangzhou 311305, China;
3. Oxygen Generation Plant, Gas Supply Company, Nanjing Iron & Steel United Company Limited, Nanjing 210035, China
钢铁生产过程中需要氧、氮、氩多种产品[1],随着钢铁市场的频繁波动,企业需要精细化生产调度[2-4],期望空分供气网络能够及时地跟踪下游钢铁生产的需求变化[5],在保证生产平衡的情况下减少资源浪费和经济损失,使得生产效益最大化。因此,如何根据钢铁生产以及空分供气网络各装置的特点建立合理的调度方案安排各装置的运行状况,已成为空分供气网络生产调度领域的研究热点之一。
对于国外供气系统来讲,通常是大范围内集中辐射形式的供氧,考虑通常是时变电价的空分装置调度问题以及能源存储的生产调度问题。例如,Pinto等[6]、Miller等[7]和Misra等[8-14]提出了一种考虑电价每小时变化的电力密集型连续过程的长期调度模型。与国外不同的是,国内所考虑的通常是小范围内空分装置的调度问题[15-16],国外考虑的场景通常为钢铁厂自备空分厂的厂级的空分装置调度问题,从影响因素看,由于国内目前电价仍然以不变电价为主,因此考虑的问题也与国外不同。Zhou等[17]、周丹艳等[18]对国内钢铁厂自备空分厂的多台空分装置的问题进行研究,通过模型求解,能够获得小时级的最优空分装置调度方案。张培昆等[19-20]针对用氧节能、下游出现生产状况以及空分短期停车对整体企业级生产的影响。从建模方法上来看,空分供气网络调度模型主要采用面向连续工业生产流程的离散时间建模方法。近些年,Ierapetritou等[21]、Zhuge等[22]提出了一种基于操作模式或者模态的建模方法,后由Zhang等[23-25]和Xu等[26]进一步完善和推广,在空分应用案例中,采用数据驱动的方式建立了氧、氮产品的二维凸区域代理模型。
针对上述问题,本研究提出一种多产品空分供气网络的短期调度方法。采用本课题组[27]提出的空分装置多产品的简化机理模型,建立原料空气与5种产品间物料平衡关系,最终形成完整的空分装置的生产模型;考虑了氮压机复用模式,应对氧氮需求比例失调的场景;最后,针对某钢铁集团的供气网络,研发了多产品联合调度系统,以短期需求预测触发生产调度优化命题求解,通过调整设备的运行方式和生产负荷,满足下游用户的动态需求变化。
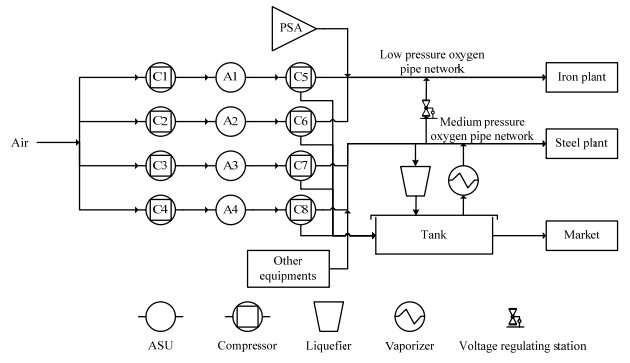
2 空分供气网络空分供气网络是氧、氮、氩等3种产品的复杂供气网络,均来源于空分装置,通过各自的网络供给下游钢铁生产,以下将分别对3种网络详细介绍。氧气供应网络如图 1所示,其源头为空气,其中主要设备为空分装置(air separation unit,ASU)(A1~A4),由于配备的压缩机(C1~C8)不同,系统可以分别产出中压氧气、低压氧气2种类型的氧气,同时每台装置均会产生液氧;产出的气体、液体通常会送入氧气管网以及储槽中。氧气管网有2种,分别为低压氧气管网以及中压氧气管网,其中低压氧气管网不具备缓冲能力,会直接输送给下游用户;中压氧气管网具备缓冲能力,同时也可以通过液化器、气化器进行气、液交换,保证管网压力,同时低压氧气管网与中压氧气管网之间通过调压站连接,具备中压氧气转化为低压氧气的能力。最终通过氧气管网将气体输送至炼钢厂、炼铁厂、企业外部用户等,液体则直接进入市场销售。
|
图 1 氧气供应网络 Fig.1 Oxygen supply network |
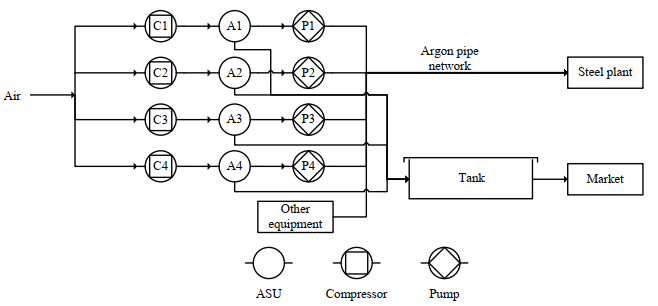
氩气供应网络比较简单,如图 2所示,氩气发生系统也是空分装置,其直接产品只有液氩,每台空分装置会配备一台液氩泵(P1~P4),液氩通过液氩泵转化为氩气,直接输送给下游用户。
|
图 2 氩气供应网络 Fig.2 Argon supply network |
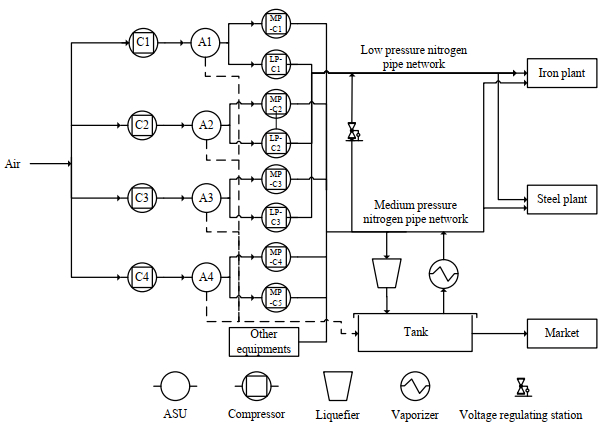
氮气供应网络与氧气供应网络类似,如图 3所示,网络源头仍然为空分装置,每台空分装置会配备数量不同的中压氮压机(MP-C1~MP-C4)和低压氮压机(LP-C1~LP-C3),根据不同的压缩机,可以产出中压氮气与低压氮气。氮气管网分为2种:中压氮气管网和低压氮气管网。随着下游用户氮气需求增加,受限于空分装置本身的氧压机与氮压机配置比例,往往需要开启其他的空分装置带动隶属于该空分装置的氮压机产生氮气。为了改善该情况,企业会将通往氮压机的管道进行联通,使得多台空分装置可以共用多台氮压机。如果空分装置生产的氮气量超过了氮压机的运行负荷,多余的氮气会流向水冷塔。中压氮气管网和氧气管网类似,可以储存一定量的氮气,从而通过其自身的缓冲作用、液化器和气化器进行生产调节。低压氮气管网本身容纳气体的能力有限,一般不具有缓冲作用,在低压氮气产量不足时,中压氮气可以通过调压站调节至低压后进入低压氮气管网用以补足需求。
|
图 3 氮气供应网络 Fig.3 Nitrogen supply network |
多产品空分管网实时生产调度是在满足生产约束的情况下,通过决策系统中各个装置的操作模式、生产水平,达到最大化生产利润的目的,短期调度中不考虑空分装置的启停问题,仅做负荷的调整。结合空分供气网络的流程,问题的决策变量为:空分装置的生产负荷,压缩机的启停和生产负荷,液化器和气化器的启停和生产负荷,调压站的气体转化量,液体产品的销售量。
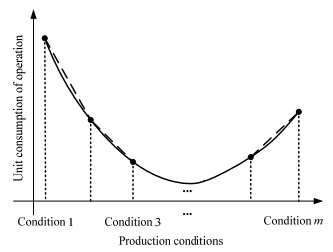
3.1 空分装置的调度模型空分装置是将空气转化为氧、氮、氩等多种气、液体产品的生产装置,由于本研究考虑的是多产品空分供气网络,因此涉及5种产品(氧气、液氧、氮气、液氮、液氩)和一种生产资源(空气)之间的物料平衡关系。从空分装置的原料端出发,利用进料空气量划分模态,这种模态划分的方式能够减少空分装置运行模态的个数,使模型的描述更加简单。空分装置的能耗主要是压缩机的能耗。空分装置在不同工况下其运行单耗变化如图 4所示,装置的运行单耗和运行负荷为非线性关系,当实际运行负荷越接近标准工况设计负荷时,运行单耗越小,反之,运行单耗会相应地增大,而带来该非线性关系与压缩机本身的单耗及生产水平有关,因此可以将空分装置的单耗与生产水平的非线性关系近似地转化为分段线性关系。
|
图 4 空分装置运行能耗图 Fig.4 Energy consumption of air separation unit |
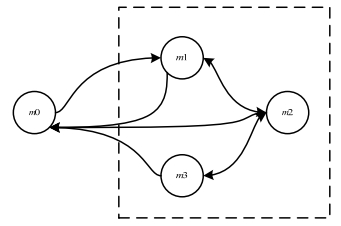
在建模过程中,空分装置的运行用进料空气量来表示,相应地,运行单耗表示为空压机的耗电量,如图 4所示为运行单耗与生产工况的关系,空分装置正常运行时,可以根据空分装置的能耗与装置消耗空气量的关系划分为m−1个模态。模态划分数量需要根据装置具体特性进行选择,没有通用的选取原则。原则上,模态划分的数量越多,对装置的描述越精细,解的最优性越好,但是问题计算量会大大增加。因此,需要综合考虑确定模态数量。在整个调度时间内,空分装置可以在不同的运行模态中切换。假设空分装置存在4种模态,分别为停机模态m0以及不同负荷下的正常运行模态m1、m2、m3,模态的转换关系如图 5所示。
|
图 5 空分装置模态转换图 Fig.5 Mode transformation of air separation unit |
在给定的调度时间间隔内,空分装置只能运行在一种模态下,当空分装置处于正常运行状态时(正常运行时的模态记作m1,m2…等)。通过历史数据回归空气与产品之间的关系,通常情况下,由于氮气过剩,通常会尽可能地多制造液氮,在假设液氮的冷量最大化的情况下,可以回归得到式(5)~(8) 4条约束,分别代表了氮氧平衡、液体平衡、氮平衡和氩平衡;式(1)~(2) 将各个模态下的生产状态进行加和得到当前时刻下装置的生产状态;式(3)~(4) 描述了不同模态下的空气量与单耗之间的关系。由此将空分装置的能耗模型与生产模型通过模态划分的方式关联到一起,最终建立了完整的空分装置模型。
| $ {F_{u, t}} = \sum\limits_{m \in {M_u}} {{{\bar F}_{u, m, t}}} $ | (1) |
| $ Q_{u, t}^{} = \sum\limits_{m \in {M_u}} {\bar Q_{u, m, t}^{}} $ | (2) |
| $ {\bar F_{u, m, t}} = \left( {{f_{u, m - 1}} - {f_{u, m}}} \right){\bar \lambda _{u, m, t}} + {f_{u, m}}{y_{u, m, t}} $ | (3) |
| $ \bar Q_{u, m, t}^{} = \left( {q({f_{u, m - 1}}) - q({f_{u, m}})} \right){\bar \lambda _{u, m, t}} + q({f_{u, m}}){y_{u, m, t}} $ | (4) |
| $ {\bar F_{u, m, {\rm AIR}, t}} = {a_1}{\bar F_{u, m, {\rm GOX}, t}} + {b_1}{\bar F_{u, m, {\rm LIN}, t}} + {c_1}{y_{u, m, t}} $ | (5) |
| $ {a_2}{\bar F_{u, m, {\rm AIR}, t}} + {b_2}{y_{u, m, t}} = {\bar F_{u, m, {\rm LOX}, t}} + {\bar F_{u, m, {\rm LIN}, t}} $ | (6) |
| $ {a_3}{\bar F_{u, m, {\rm AIR}, t}} + {b_3}{y_{u, m, t}} = {\bar F_{u, m, {\rm GAN}, t}} + {\bar F_{u, m, {\rm LIN}, t}} $ | (7) |
| $ {a_4}{\bar F_{u, m, {\rm AIR}, t}} + {b_4}{y_{u, m, t}} = {\bar F_{u, m, {\rm LAR}, t}} $ | (8) |
| $ {F_{u, g, t}} = \sum\limits_m {{{\overline F }_{u, m, g, t}}} $ | (9) |
式中:yu, m, t表示t时刻装置u是否在模态m下;Fu, t表示t时刻进入装置u的气体量,m3·h−1;Qu, t表示t时刻装置u消耗的电量,kW·h;fu, m表示装置u在模态m的边界上的操作点的气体量,m3·h−1;q(fu, m)表示装置u在模态m的边界上的操作点空压机/氧压机的耗电量,kW·h,λu, m, t表示装置u在模态m的边界上的操作点的权重,为布尔变量,无量纲;
变压吸附(pressure swing adsorption,PSA)装置有停机和正常生产2种模态。当装置停机时,氧气产量均为0,运行单耗为0,当装置正常运行时,产品产量均为固定值,运行单耗也是固定值,其生产空间可以表示如下:
| $ {F_{s, g, t}} = \sum\limits_{m \in {M_s}} {{{\bar F}_{s, m, g, t}}} {\text{ }}\forall s \in {\rm NC}{, _{}}t \in \bar T $ | (10) |
| $ {\bar F_{s, m, g, t}} = {F_{s, m}}{y_{s, m, t}}{\text{ }}\forall s \in {\rm NC}{, _{}}m \in {M_s}, {}_{}t \in \bar T $ | (11) |
| $ \sum\limits_{m \in {M_s}} {{y_{s, m, t}}} = 1{\text{ }}\forall s \in {\rm NC}{, _{}}t \in \bar T $ | (12) |
| $ {y_{s, m, t}} \in \{ 0, 1\} {\text{ }}\forall s \in NC{, _{}}m \in {M_s}{, _{}}t \in \bar T $ | (13) |
式中:Fs, m表示装置s在模态m下生产氧气的产量,m3·h−1;
液化器、气化器用来与管网进行气液交换,液化器与气化器的负荷是固定的,只消耗气体或者液体,几乎没有电耗,因此可用以下的约束条件描述气化器和液化器:
| $ F_{a, t}^g = f_a^gy_{a, t}^g $ | (14) |
| $ y_{a, t}^g \in \{ 0, 1\} $ | (15) |
式中:
气化器的物料方程如下所示:
| $ F_{b, t}^g = f_b^gy_{b, t}^g $ | (16) |
| $ y_{b, t}^g \in \{ 0, 1\} {\text{ }} $ | (17) |
式中:
对于氮压机,分为低压氮压机和中压氮压机,但其能耗变化范围很小,因此可以认为是固定能耗。在多台空分装置的气体网络中,受限于本身氧压机与氮压机的配置比例,为了改善在氮气需求过高情况下额外开启空分装置的问题,通常会考虑氮压机复用,即多台空分装置共用多台氮压机。因此可以通过如下的方程建立氮压机复用模型:
| $ \sum\limits_{u \in {\rm ASU}} {{F_{u, {\rm GAN}, t}}} + \tilde F_t^{{LIQ}} = \sum\limits_{v \in {\rm MPNC}} {{F_{v, t}}} + \sum\limits_{w \in {\rm LPNC}} {{F_{w, t}}} + {F_{{\rm CT}}} $ | (18) |
式中:中压氮压机的集合和低压氮压机的集合分别用MPNC和LPNC表示,Fv, t和Fw, t分别表示t时刻中压氮压机v和低压氮压机w压缩的氮气量,m3·h−1;FCT表示流向水冷塔的气体量,m3·h−1;
氮压机的能耗表示如下所示:
| $ Q_{v/w, t}^{} = q_{v/w}^{}{F_{v/w, t}} $ | (19) |
式中:Qv/w, t表示t时刻氮压机v/w的耗电量,qv/w表示氮压机v/w的单耗,Fv/w, t表示t时刻氮压机v/w压缩的氮气量。
3.5 气液体供需平衡模型气体平衡包括上游生产气体与下游气体需求之间的关系。气体生产包括空分装置、变压吸附装置等,可以用如下约束描述:
| $ {D_{g, t}} = \sum\limits_{u \in {\rm ASU}} {{F_{u, g, t}}} + {F_{{\rm PSA}, g, t}} + \sum\limits_{v \in {\rm VAP}} {F_{v, t}^g} - \sum\limits_{w \in {\rm LIQ}} {F_{w, t}^g} + M{L_t} - V{T_t}_{} $ | (20) |
式中:Dg, t表示t时刻g气体需求,FPSA, g, t表示变压吸附装置t时刻生产的气体,
液体主要用于销售以获取利润,因此液体平衡主要包括气化器、液化器以及液化器外的液体交换的平衡,可以用如下约束描述:
| $ {S_{l, t}} = \sum\limits_{u \in {\rm ASU}} {{F_{u, l, t}}} + \sum\limits_{v \in {\rm LIQ}} {F_{v, t}^l} - \sum\limits_{w \in {\rm VAP}} {F_{w, t}^l} {\text{ }}\forall t \in \bar T{, _{}}l \in L $ | (21) |
| $ \sum\limits_{w \in {\rm VAP}} {F_{w, t}^l} = \sum\limits_{w \in {\rm VAP}} {F_{w, t}^l} + {B_{l, t}}{\text{ }}\forall t \in \bar T, l \in L $ | (22) |
式中:Sl, t表示销售的液体量,t;Fu, l, t表示空分装置u产生的液体量,t;
调度的目标是在满足生产要求的同时能够利润最大化,获取最优的运行方案,目标函数由收入减去成本得到
| $ \max\quad {\rm profit} = {\rm rev} - {\rm cost} $ | (23) |
式(23)中收入包括销售空分装置直接生产的气体和液体的收入rev1,液体的收入rev2;成本包括压缩机的运行能耗cost1,空分装置的启动成本cost2,杭氧液化氧成本cost3以及外购液氧成本cost4。
| $ {\rm rev}_1 = \sum\limits_{t \in \bar T} {D_{g, t}^{}{c_g}} $ | (24) |
| $ {\rm rev}_2 = \sum\limits_{t \in \bar T} {\sum\limits_{\rm LIQ \in LOX, LIN, LAR} {S_{l, t}^{}{c_l}} } $ | (25) |
| $ {\rm cost1} = \sum\limits_{t \in \bar T} {\sum\limits_{u \in {\rm ASU}} {Q_{u, t}^{} \times {c_{\rm ep}}} } + \sum\limits_{t \in \bar T} {Q_{v/w, t}^{} \times {c_{\rm ep}}} $ | (26) |
| $ {\rm cost2} = \sum\limits_{t \in \bar T} {\sum\limits_{u \in {\rm ASU}} {{z_{u, {m_1}, {m_2}, t}}{c_h}{{_{, u}}}} } $ | (27) |
| $ {\rm cost3} = \sum\limits_{t \in \bar T} {{F_{hy, {\rm GOX}, t}} \times {c_1} + {F_{nh, {\rm GOX}, t}} \times {c_2}} $ | (28) |
| $ {\rm cost4} = \sum\limits_{t \in \bar T, l \in L} {{B_{l, t}} \times {c_3}} $ | (29) |
式中:Dg, t为t时刻气体g的需求量,m3·h−1;cg为气体g的价格,元;cl为液体l的价格,元;cep为电价, 元·(kW·h)−1;
综上完成了多产品空分管网调度模型的构建。
4 生产调度系统调度系统包括前端、交互、调度逻辑处理、数据库以及本地运行环境。其中主要的调度算法嵌入调度逻辑层中,短期调度作为其中的一块子功能嵌入整个系统中。短期调度功能模块由2块组成,分别为周期性再调度和触发式再调度。
触发式再调度依赖于实时监控及异常情况报警;周期性再调度则是定期地完成再调度。整体调度模型的输入仍然为气体需求,在短期调度场景下无法依赖于人工的输入,因此需要建立独立的需求预测模块,本研究采用文献[27]提出的基于粒度计算理论的预测方法建立了需求预测模块。
5 应用与分析以某钢铁集团制氧厂的4台空分实例化模型,空分装置参数如表 1、2所示。
|
|
表 1 某钢铁集团制氧厂空分系统参数 Table 1 Air separation system parameters of an oxygen plant of Nanjing Iron and Steel Group |
|
|
表 2 某钢铁集团制氧厂氮压机参数 Table 2 Nitrogen compressor parameters of an oxygen plant of Nanjing Iron and Steel Group |
该场景下设置调度时域为16 h,调度时间间隔为1 h,气体预测需求如表 3所示。从需求角度来看,整体氧气需求在标准状态下为65 000~70 000 m3·h−1,氮气需求在标准状态下为105 000~110 000 m3·h−1,一般情况下空分装置的氧压机和氮压机配比在1.3~1.5,在该场景下,整体的氮氧需求配比超过了1.6。如果不进行氮压机复用,则需要额外开启空分装置,利用附带的氮压机产出氮气供给下游。在氮压机复用模式下,将氮压机的入口联通,可以在空分装置未开启的情况下启动氮压机,减少不必要的资源浪费。
|
|
表 3 气体需求(场景1) Table 3 Gas demand list (Scenario 1) |
利用上述气体需求触发求解调度命题,求解结果如表 4所示,其中ASU2和MPGN1处于关机状态。
|
|
表 4 调度结果(场景1) Table 4 Scheduling result (Scenario 1) |
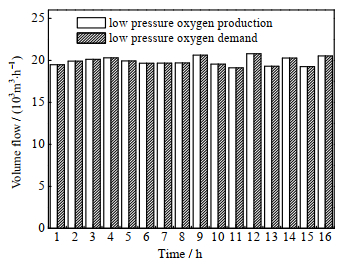
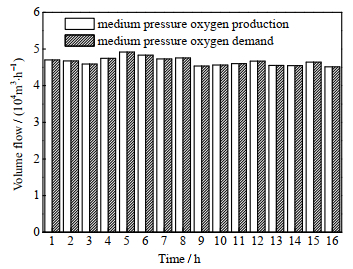
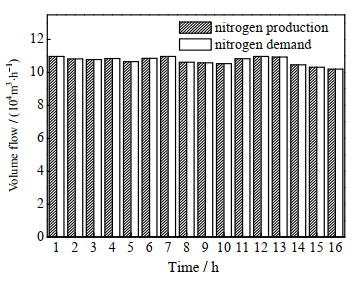
从图 6~8中可以看出,整体空分装置的气体产出与下游的需求保持一致。在低压氧气需求变化时,会通过1#空分装置的负荷调整来满足需求;在中压氧气需求增负荷时,会优先增加4#空分装置的负荷,在降负荷的阶段,会优先降低3#空分装置的负荷,原因在于4#空分装置的能耗低于3#空分装置。
|
图 6 低压氧气平衡图(场景1) Fig.6 Low pressure oxygen balance diagram (Scenario 1) |
|
图 7 中压氧气平衡图(场景1) Fig.7 Medium pressure oxygen balance diagram (Scenario 1) |
|
图 8 氮气平衡图(场景1) Fig.8 Nitrogen balance diagram (Scenario 1) |
观察氮压机的负荷调整,由于低压氮压机的能耗相对较低,中压氮压机的能耗相对较高,因此在整个调度时域内,低压氮压机保持满负荷生产,中压氮压机进行负荷调整,保持和气体需求的一致性。1#和5#中压氮压机的能耗相对较低,在氮气需求较高的情况下保持满负荷生产,由3#和4#中压氮压机负责负荷调整满足需求,4#中压氮压机能耗低于3#中压氮压机,因此在升负荷的过程中,优先提高4#中压氮压机的负荷,在降负荷的阶段,优先降低3#中压氮压机的负荷。
场景1的氮压机复用模式为:启动2#空分装置配备的2#低压氮压机(LPGN2),弥补氮压机的产能不足,此时2#空分装置处于停机状态,并未运行。
5.2 场景2该场景下设置调度时域为16 h,调度时间的间隔为1 h。气体预测需求和求解结果分别见表 5、6。
|
|
表 5 气体需求(场景2) Table 5 Gas demand list (Scenario 2) |
|
|
表 6 调度结果(场景2) Table 6 Scheduling result (Scenario 2) |
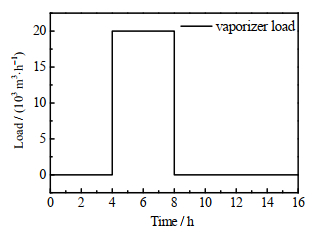
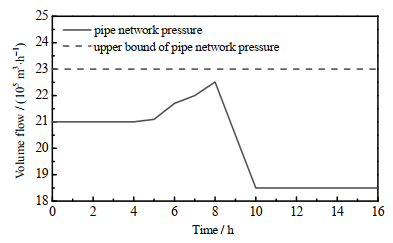
图 9、10分别为气化器调度结果与中压氧气管网压力,在0~4 h内,整体的氧气需求在90 000~100 000 m3·h−1,氧气需求小于4台空分装置的制氧能力,不需要开启气化器补充气体。低压氧气与中压氧气生产相互独立,此时由于2#空分装置的能耗较高,因此会优先采用1#空分装置生产,2#空分装置补足低压氧气缺口;对于中压氧气,由于3#空分装置的能耗高于4#空分装置,因此保证4#空分装置满负荷生产,3#空分装置作为可调整量随需求进行变化。
|
图 9 气化器调度结果(场景2) Fig.9 Vaporizer scheduling result (Scenario 2) |
|
图 10 中压氧气管网压力(场景2) Fig.10 Pressure of medium pressure oxygen network (Scenario 2) |
在4~10 h内,氧气需求在100 000~120 000 m3·h−1,超出了4台空分装置的最大制氧能力,需要额外开启一台20 000 m3·h−1产能的固定负荷气化器。预计在8 h左右管网压力超过安全线时,应当提前关闭气化器,避免管网放散。
6 结论本研究从多产品空分管网的流程出发,对整体供气网络中的各个装置基于模态建立了混合整数线性规划模型,以最大化生产利润为目标,建立了生产调度的优化命题。针对调度的现场实施,提出了整体解决方案,包括具体应用的整体架构以及各个功能模块。通过实际的场景分析,验证了调度方案的合理性,且调度结果具备指导意义。
| [1] |
化国, 崔仁鲜. 浅析空分装置在钢铁企业中的应用[J]. 低温与特气, 2015, 33(5): 50-52, 54. HUA G, CUI R X. Some discussions about the application of air separation unit for steel industrial[J]. Low Temperature and Specialty Gases, 2015, 33(5): 50-52, 54. |
| [2] |
邹环泽. 深冷空分的过程模拟与节能分析[D]. 重庆: 重庆大学, 2017. ZOU H Z. The simulation and analysis of the process cryogenic air separation [D]. Chongqing: Chongqing University, 2017. |
| [3] |
张延平, 凌晨, 周建波, 等. 钢铁企业大型空分的能耗分析与经济运行[J]. 冶金能源, 2014, 33(5): 6-8, 17. ZHANG Y P, LIN C, ZHOU J B, et al. Energy consumption and optimize circulate of air separation unit of steel corporation[J]. Energy for Metallurgical Industry, 2014, 33(5): 6-8, 17. |
| [4] |
程杰平. 空分设备自动变负荷控制系统的设计与实现[D]. 沈阳: 东北大学, 2010. CHENG J P. Design and implementation of automatic load control system for air separation unit [D]. Shenyang: Northeastern University, 2010. |
| [5] |
赵倩倩. 空分管网的多产品调度优化研究[D]. 杭州: 浙江大学, 2020. ZHAO Q Q. Multi-product optimal scheduling research for gas network with air separation units [D]. Hangzhou: Zhejiang University, 2020. |
| [6] |
PINTO J M, MITRA S, GROSSMAN I E. Optimal multi-scale capacity planning for power-intensive continuous processes undertime-sensitive electricity prices and demand uncertainty. Part Ⅱ: Enhanced hybrid bi-level decomposition[J]. Computers and Chemical Engineering, 2014, 65: 89-101. DOI:10.1016/j.compchemeng.2014.01.016 |
| [7] |
MILLER J, LUYBEN W L, BLOUIN S. Economic incentive for intermittent operation of air separation plants with variable power costs[J]. Industrial and Engineering Chemistry Research, 2008, 47(4): 1132-1139. DOI:10.1021/ie070593n |
| [8] |
MISRA S, KAPADI M, GUDI R D, et al. Production scheduling of an air separation plant[J]. IFAC PapersOnLine, 2016, 49(7): 675-680. DOI:10.1016/j.ifacol.2016.07.256 |
| [9] |
MITRA S, GROSSMANN I E, PINTO J M, et al. Optinal production planning under time-sensitive electricity prices for continuous power-intensive processes[J]. Computers and Chemical Engineering, 2012, 38(7): 171-184. |
| [10] |
MISRA S, SAXENA D, KAPADI M, et al. Short term planning framework for enterprise wide production & distribution network of a cryogenic air separation industry[J]. Industrial and Engineering Chemistry Research, 2018, 57(49): 16841-16861. DOI:10.1021/acs.iecr.8b05138 |
| [11] |
MISRA S, KAPADI M, GUDI R D, et al. Resource optimization & inventory routing of packaged liquefied gas supply chain[J]. Industrial and Engineering Chemistry Research, 2019, 58(18): 7579-7592. DOI:10.1021/acs.iecr.8b05604 |
| [12] |
MITRA S, SUN L, GROSSMANN I E. Optimal scheduling of industrial combined heat and power plants under time-sensitive electricity prices[J]. Energy, 2013, 54(2): 194-211. |
| [13] |
MITRA S, PINTO J M, GROSSMANN I E. Optimal multi-scale capacity planning for power-intensive continuous processes under time-sensitive electricity prices and demand uncertainty. Part Ⅰ: Modeling[J]. Computers and Chemical Engineering, 2014, 65(4): 89-101. |
| [14] |
MISRA S, PRAVIN P S, GUDI R D, et al. Integration of supply and demand side management using renewable power sources: Application on an air separation plant[J]. Industrial and Engineering Chemistry Research, 2021, 60(9): 3670-3686. DOI:10.1021/acs.iecr.0c05810 |
| [15] |
陈聪. 钢铁企业氧气管网的平衡与调度研究[D]. 杭州: 浙江大学, 2013. CHEN C. Balance of the oxygen pipe-network and scheduling in iron and steel enterprises [D]. Hangzhou: Zhejiang University, 2013. |
| [16] |
陈聪, 赵均, 邵之江. 钢铁企业氧气管网的平衡与调度研究[J]. 计算机与应用化学, 2012, 29(9): 6-6. CHEN C, ZHAO J, SHAO Z J. Balance of the oxygen pipe network and scheduling in iron and steel enterprises[J]. Computers and Applied Chemistry, 2012, 29(9): 6-6. |
| [17] |
ZHOU D Y, ZHOU K, ZHU L Y, et al. Optimal scheduling of multiple sets of air separation units with frequent load-change operation[J]. Separation and Purification Technology, 2017, 172: 178-191. DOI:10.1016/j.seppur.2016.08.009 |
| [18] |
周丹艳. 联产空分装置的变负荷调度研究[D]. 杭州: 浙江大学, 2016. ZHOU D Y. Optimal scheduling of multiple air separation units under frequently changing demands [D]. Hangzhou: Zhejiang University, 2016. |
| [19] |
张培昆, 王立. 空分短期停车时间阈值对氧气生产调度的影响[J]. 化工学报, 2017, 68(6): 2423-2433. ZHANG P K, WANG L. Effects of temporary shutdown time-threshold on oxygen production schedule in air separation unit[J]. CIESC Journal, 2017, 68(6): 2423-2433. |
| [20] |
张培昆, 王立. 高炉休风时供氧管网压力对氧气调度的影响[J]. 工程科学学报, 2017(2): 283-293. ZHANG P K, WANG L. Effects of pipe-network on the oxygen scheduling during blast furnace blow-down[J]. Chinese Journal of Engineering, 2017(2): 283-293. |
| [21] |
IERAPETRITOU M G, WU D, VIN J, et al. Cost Minimization in an energy-intensive plant using mathematical programming approaches[J]. Industrial and Engineering Chemistry Research, 2002, 41(21): 5262-5277. |
| [22] |
ZHUGE J J, IERAPETRITOU M G. Integration of scheduling and control with closed loop implementation[J]. Industrial and Engineering Chemistry Research, 2012, 51(25): 8550-8565. |
| [23] |
ZHANG Q, SUNDARAMOORTHY A, GROSSMANN I E, et al. A discrete-time scheduling model for continuous power-intensive process networks with various power contracts[J]. Computers and Chemical Engineering, 2016, 84: 382-393. |
| [24] |
ZHANG Q, CREMER J L, GROSSMANN I E, et al. Risk-based integrated production scheduling and electricity procurement for continuous power-intensive processes[J]. Computers and Chemical Engineering, 2016, 86: 90-105. |
| [25] |
ZHANG Q, GROSSMANN I E, HEUBERGER C F, et al. Air separation with cryogenic energy storage: Optimal scheduling considering electric energy and reserve markets[J]. AIChE Journal, 2015, 61(5): 1547-1558. |
| [26] |
XU Z, ZHAO J, XI C, et al. Automatic load change system of cryogenic air separation process[J]. Separation and Purification Technology, 2011, 81(3): 451-465. |
| [27] |
ZHOU P, XU Z, ZHAO J, et al. Long-term hybrid prediction method based on multiscale decomposition and granular computing for oxygen supply network[J]. Computers and Chemical Engineering, 2021, 153: 107442. |




