近年来,基于数据驱动的过程监控方法因其建模思想的灵活性、有效性,在化工过程监控领域得到了广泛的应用[1],其中多变量统计过程监测方法[2](multivariate statistical process monitoring,MSPM)利用多元投影技术,将高维数据映射到低维空间进行表示,以尽可能少的变量来刻画数据的整体信息[3]。主元分析(PCA)[4]和偏最小二乘法(PLS)[5]这两种方法是该思想的典型代表。两种方法都将数据投影到较低维的子空间上,并使用T 2和SPE指标来分离正常和异常情况。但这两种方法都要事先假设过程变量是线性相关且服从高斯分布,而对于那些过程变量呈现非线性、非高斯分布的情况则效果甚微。为实现对这些复杂过程的监控,一些针对传统PCA和PLS的改进方法和新方法逐渐被提出。核主元分析(KPCA)方法[6]、基于神经网络的非线性PCA方法[7]、基于加权差分的PCA方法[8]、核偏最小二乘(KPLS)方法[9]和移动窗递推偏最小二乘(RPLS)方法[10]等用来解决非线性问题;KANO等将独立成分分析(ICA)方法[11]引入到过程监控领域,解决了非高斯问题,在此基础上LEE等[12]定义了ICA模型的I2, Ie2和SPE监控指标,GE等[13]提出基于ICA-PCA的两步法的监控构架,JIE等[14]利用有限个高斯元刻画数据的分布模型,以另一种思路解决了非高斯问题。但是现有的MSPN方法,本质是采用了降维或高斯假设的思想,因此直接刻画复杂过程变量之间的相关性行为,建立相关性结构模型,有着很高的研究价值。
近几年,作为相关性建模的有效工具,Copula函数将联合分布函数与边缘分布函数及其相关性结构联系起来,在金融、经济和气象领域中得到了广泛应用[15-17],并逐渐被引入到化工过程监控领域。但是传统多元Copula函数参数的优化过程低效和繁琐,当数据维数过高时,会陷入“维数灾难”。为了解决多元Copula函数的优化问题,JOE等[18]于1996年提出了Vine Copula分解方法,将多元Copula函数分解成若干个二元Copula函数的组合形式,多元Copula函数参数的优化问题就简化为一系列二元Copula函数参数的求解问题。这一点也促进了Copula在化工过程监控领域的应用。任翔等[19]建立了VCDD (Vine Copula based dependence description)相关性模型,将C-Vine模型引入到过程监控领域,在不降维的基础上直接描述过程变量之间存在的复杂相关性,并构建了一类适用于非高斯、非线性过程的广义贝叶斯推断概率指标,实现了对化工过程的实时故障检测。郑文静等[20]采用了混合D-Vine结构的Copula函数方法对复杂工业过程进行建模,将D-Vine Copula与有限元混合模型相结合,提高了Vine Copula模型结构的灵活性,更充分地提取变量之间的相关信息。Copula函数种类繁多,选取合适的Copula函数是关键。目前最常用的Copula函数选择方法是基于最大伪似然的AIC (Akaike information criterion)信息准则,但是在利用AIC准则选择最优Copula函数时,不仅要计算每个备选Copula函数的密度函数,而且边缘分布函数的拟合效果严重影响了AIC的取值,因此当备选Copula函数的密度函数比较复杂或者边缘分布的拟合效果较差时,此时AIC准则的使用就受到了限制[21]。
本文提出基于核密度估计的Copula函数选择原理,其核心思想是先利用核密度估计方法估计各变量的边缘密度分布函数,进而得到边缘分布函数,最后利用真实分布函数的基于乘积的核密度的估计值和备选Copula函数之间的范数来选择最优的Copula函数。同时为了全面挖掘数据变量之间的相关性信息,采用应用范围更广的R-Vine分解模型。相比于C/D-Vine固定的星型和直线型结构,R-Vine分解结构是根据变量间的真实相关行为确定的,因此R-Vine模型在描述相关性方面灵活性更强,与变量实际相关行为更为接近,能更全面挖掘随机变量间的相关性信息。将R-Vine Copula与核密度估计方法相结合,为统计建模赋予了更强的灵活性。针对复杂工业过程数据建立KRVC模型,利用高密度区域(HDR)与密度分位数等理论,构建了非高斯态广义局部概率指标(GLP)。通过在TE过程和醋酸脱水过程中的的应用,表明KRVC模型在过程监控中有较好的检测效果。
2 R-Vine Copula理论及其选择方法Copula函数是建立在[0, 1]上的多元联合分布函数,每一个联合分布函数都隐秘的包含了变量的边缘分布信息,以及关联这些边缘分布行为的相关结构,而Copula函数则将这些分布行为和结构用理论化的方式联系了起来[22]。根据SKLAR定理[23],d维随机向量X=(X1, X2, …, Xd)T的联合分布函数可以用Copula函数表示
| $F({x_1}, {x_2}, \cdots , {x_d}) = C({u_1}, {u_2}, \cdots , {u_d}) $ | (1) |
其中ui = F(xi) (i=1, 2, …, d)表示变量xi的边缘分布函数,并满足以下条件
| ${u_i} = {F_i}({x_i}) = \int_0^{{x_i}} {{f_i}} ({x_i})\mathrm{d}{x_i} $ | (2) |
fi(xi)表示变量xi的边缘密度分布函数。当C在Rd上可微时,式(1)两边分别对x∈Rd求导,对应的联合密度分布函数f(x)可以表示成边缘密度分布函数fi(xi)和Copula密度函数c的乘积形式
| $f(x) = c({u_1}, {u_2}, \cdots {u_d})\prod\limits_{i = 1}^d {{f_i}({x_i})} $ | (3) |
式中的密度函数c定义为
| $c({u_1}, {u_2}, \cdots , {u_d}) = \frac{{{\partial ^d}C({u_1}, {u_2}, \cdots , {u_d})}}{{\partial {u_1}\partial {u_2} \cdots \partial {u_d}}} $ | (4) |
一旦Copula分布函数的形式固定,通过极大似然法对式(3)中的参数进行估计,就可以得到多维数据的联合密度分布函数。但是当数据维数过高时,优化过程会变得极其复杂,容易陷入“维数灾难”。1996年Joe等[18]提出了Vine Copula分解方法,将二元Copula函数扩展到多元形式,为多元Copula函数估计问题提出了一种解决思路。
2.1 R-Vine Copula根据BEDFORD和COOKE[24]的定义,R-Vine包含一系列的树,每棵树的每一条边都连接着对应的二元Copula函数,一个d维变量的R-Vine结构由d-1棵树组成,这里定义为T = (T1, T2, …, Td-1);第j棵树Tj有d+1-j个节点和d-j条边,记为Nj、Ej,(j=1, 2, …, d-1);上一棵树的边是下一棵树的节点,比如,树Tj的节点Nj是上一棵树Tj-1的边集Ej-1。因此当结构满足以下条件时,就称之为R-Vine结构:
(1) 树T1的边集为E1,节点集N1={1, 2, …, d-1};
(2) 树Tj的节点集等于树Tj-1的边集Ej-1,边集为Ej,(j=1, 2, …, d-1);
(3) 如果树Tj-1的两条边ei、ej共享一个节点,则在树Tj中这两个节点用边连接。
对一个d维变量建立R-Vine模型,这里定义节点集N = {N1, N2, …, Nd-1},边集E = {E1, E2, …, Ed-1},Ni,Ej分别为树Tj的节点集和边集。边集Ei中的一条边记为ei = j(e), k(e)|D(e),j(e)和k(e)是连接该边的两个节点,D(e)为条件集,边ei对应的二元Copula密度函数为cj(e), k(e)|D(e)。d维随机向量X= (X1, X2, …, Xd)T的R-Vine分解模型的联合分布概率密度函数可以表示为:
| $f({x_1}, {x_2}, \cdots , {x_d}) = c[{F_1}({x_1}), {F_2}({x_2}), \cdots , {F_d}({x_d}), \theta ]\prod\limits_i^d {{f_i}({x_i})} $ | (5) |
其中
| $c({F_1}({x_1}), {F_2}({x_2}), \cdots , {F_d}({x_d})) = \prod\limits_{i = 1}^d {\prod\limits_{e \in {E_i}} {{c_{j(e), k(e)|D(e)}}} } [F({x_{j(e)}}|{x_{{D_{(e)}}}}, F({x_{k(e)}}|{x_{{D_{(e)}}}}), {\theta _{(e)}}]\ $ | (6) |
式中,xD(e)表示由条件集D(e)决定x= (x1, x2, …, xd)T的子向量,θ(e)表示对应的二元Copula函数的参数,fi(xi)为随机变量Xi的边缘概率密度函数。
式(6)中的Copula函数对包含了条件分布函数项,为了得到这些条件分布函数,AAS等[25]给出了计算上面这些条件分布函数方法
| ${F_{{x_j}|D}}({x_j}|{x_D}) = \frac{{\partial {C_{{x_j}, v|{D_{ - v}}}}({F_{{x_j}|{D_{ - v}}}}({x_j}|{x_{{D_{ - v}}}}), {F_{v|{D_{ - v}}}}({x_v}|{x_{{D_{ - v}}}});{\theta _{{x_{j, v|{D_{ - v}}}}}})}}{{\partial {F_{v|{D_{ - v}}}}({x_v}|{x_{{D_{ - v}}}})}} $ | (7) |
其中,xD表示条件向量集,v是xD中随机选择的一个向量,xD-为不包含元素v的向量集,并且满足xD ={v, xD-},表示基于xD-的关于xj的条件分布函数,Cxj, v|D-v则表示对应的Copula分布函数,θxj, v|D-v为二元Copula函数的参数。
在R-Vine模型的的构建过程中,为了便于记录各棵树的条件集D(e)以及二元Copula函数对cj(e), k(e)|D(e)的信息,KUROWICKA[26]和BRECHMANN[27]提出了结构树矩阵法。因为树矩阵呈现下三角形式,也称之为下三角矩阵法。令结构树矩阵为M = (mij|i, j=1, 2, …, d),mij∈{1, 2, …, d },d为变量的维数,也是矩阵的阶数。矩阵M的对角线元素是{1, 2, …, d }的某个排列,除去对角线元素,矩阵的每一行代表着一棵树,条件集D(e)由对角线元素所在列的下面元素决定。
2.2 R-Vine树形结构构建及其基于核密度估计的Copula函数选择方法根据BRECHMANN等[27]的研究,R-Vine树结构的选择应该以具有最强相依性为准则,其核心思想是捕捉树节点之间的相依性,以相关系数之和最大建立R-Vine结构模型。这里采用Kendall τ秩相关系数描述节点之间的相关性,简单地说,通过求解下面的优化问题来寻找R-Vine结构
| $\tau = \max \sum\limits_{e = \{ j, k|D\} \;in\;{T_i}} {|{\tau _{jk|D}}|} $ | (8) |
式中,τjk|D表示所有二元变量之间的Kendall τ秩相关系数。
目前针对最优Copula函数的选择问题,应用中最常用的方法基于极大似然法的AIC准则。给定备选Copula函数簇,变量F(xj(e)|xD(e))和F(xk(e)|xD(e))为对应的条件分布函数,则基于最大伪似然的AIC公式为
| $ $\[\left( {{{\hat \theta }_{{x_j}|D}},{{\hat \lambda }_{{x_j}|D}}} \right) = \arg \mathop {\max }\limits_{\begin{array}{*{20}{c}} {{\theta _{{x_j}|D}}}\\ {{\lambda _{{x_j}|D}}} \end{array}} {\mkern 1mu} \left\{ {\sum\limits_{k = 1}^N {\log } \left[ {c\left( {F_{{x_j}\left| {{D_{ - v}}} \right.}^k\left( {{x_j}|{x_{{D_{ - v}}}}} \right),F_{v|{D_{ - v}}}^k\left( {{x_v}|{x_{{D_{ - v}}}}} \right);{\theta _{{x_{jD}}}},{\lambda _{{x_{jD}}}}} \right)} \right] - \gamma } \right\}\]$ $ | (9) |
其中θxj|D和λxj|D分别表示R-Vine模型中某个二元Copula函数对的最优Copula函数结构和参数,γ表示该二元Copula对中待优化的参数个数,通常情况下γ = 1, 2。则最优的Copula函数为使得AICk取得最小时所对应的Copula函数,即
为了克服这个问题,WELLS等[28]利用非参数核密度估计的选择原理给出了一种Copula函数模型的选择方法。由于化工过程涉及的变量分布经常变化,往往呈现非线性性、非高斯性,基于参数估计的方法很难给出满意的结果,而对边缘分布不作具体假设的非参数核密度估计方法可以作为一种选择方法。其基本思想是先利用核密度函数估计二元Copula函数中的服从(0, 1)分布的分布变量,即边缘分布函数,然后通过基于乘积核的核密度的分布函数估计值与备选Copula函数之间的范数来选择最优的Copula函数。同时为了防止过拟合现象的产生,先对数据进行对立性假设检验,用独立二元Copula函数(不需要进行优化)代替对应的Copula函数,使构建的R-Vine copula树不至于过度复杂。下面给出了基于核密度估计的最优二元Copula函数选择方法的具体步骤:
(1) 先用核密度估计函数
| $\left\{ \begin{array}{l} {{\hat f}_X}(x) = \frac{1}{{N{h_X}}}\sum\limits_{i = 1}^N {{K_X}\left( {\frac{{x - {X_i}}}{{{h_X}}}} \right)} \\ {{\hat f}_Y}(y) = \frac{1}{{N{h_Y}}}\sum\limits_{i = 1}^N {{K_Y}\left( {\frac{{y - {Y_i}}}{{{h_Y}}}} \right)} \end{array} \right. $ | (10) |
式中,N为样本个数,hX,hY为基于给定样本下的窗宽,K( )为核函数。在大样本条件下,核函数的选取对核密度估计的影响微乎其微,因此这里选择应用更广泛的正态核函数,而窗宽的选取决定了核密度估计的好坏,若窗宽参数取的过大,会损失很多有用信息,反之窗宽取的越小,则整体会出现较大的偏差,本文利用RUDEMO[29]提出的交错鉴定法确定光滑参数的值。
(1) 根据条件密度分布函数获得条件分布函数,即得到二元Copula函数中服从(0, 1)分布的两个变量û,
| $\begin{array}{l} \hat u = {{\hat F}_X}({x_i}) = \int_{ - \infty }^{{x_i}} {{{\hat f}_x}(x)dx} \\ \hat v = {{\hat F}_Y}({y_i}) = \int_{ - \infty }^{{y_i}} {{{\hat f}_y}(y)dy} \end{array} $ | (11) |
(2) 用基于乘积核的核密度作为真实二元Copula分布函数的估计值,即
| $\hat F(x, y) = \frac{1}{N}\sum\limits_{i = 1}^N {\mathit{\Phi} \left( {\frac{{x - {x_i}}}{{{h_X}}}} \right)} \cdot \mathit{\Phi} \left( {\frac{{y - {y_i}}}{{{h_Y}}}} \right) $ | (12) |
(3) 计算每一个备选Copula函数和
| ${d_k} = {\left\{ {\sum\limits_{i = 1}^N {{{(\hat F - {C_k})}^2}} } \right\}^2} $ | (13) |
(4) 从备选Copula函数中选择使距离dk取得最小值的Copula函数作为最优Copula,即
| ${C_\mathrm{opt}} = \arg \mathop {\min }\limits_k ({d_k}), \;\;\;\;\;k = 1, 2, 3, \cdots $ | (14) |
高密度区域(HDR)是一种适用于任意分布的概率性度量区域,该区域能以尽可能小的体积覆盖给定概率α下的样本空间且区域内每个点的概率密度要大于等于区域外的点的概率密度。相比于其他分布预测方法,HDR是一种非常高效准确的方法。下面给出HYNDMAN[30]对HDR严格的数学定义:
令随机变量X的联合概率密度函数为f(x),则在1-δ置信水平下的HDR是R(fδ)的子集,其中
| $R\left( {{\mathit{f}_{\rm{ \mathsf{ δ} }}}} \right) = \left\{ {x|f\left( x \right) \ge {f_{\rm{ \mathsf{ δ} }}}} \right\} $ | (15) |
fδ为满足P[X∈R(fδ)] ≥ 1-δ的最大常数,1-δ实质为HDR对应的概率值。
为了计算某个分布下特定的HDR的概率值,一般采用数值积分法[31] (NIA)和密度分位数法[30] (DQA)。根据任翔等[19]的研究,由于数值积分法对高维数据具有较高的计算复杂度并且需要积分区域的完整密度分位数法信息,实际计算相当麻烦。相比之下,密度分位数法采用抽样思想实现样本空间在特定区域内的概率值估计。置信水平1-δ实质为HDR对应的概率值,因此对HDR概率值的估计等价于找到随机变量f (x)对应的一个分位数。令Y= f (X),R(fδ) = [α, β],且f(α)=f(β),则由式(15)可得到
| $P(\alpha \le X \le \beta ) = P(f(X) \ge {f_{\rm{ \mathsf{ δ} }} }) = 1 - \delta $ | (16) |
其中fδ表示随机变量Y的δ分位数,可以利用样本数据Yi = f(Xi)得到,i = 1, 2, …, n,n为样本数据个数,Xi表示第i个样本观测值,实际上这里利用了样本分位数qδy去估计随机变量Y的δ分位数fδ。
对于非高斯过程来说,基于局部马氏距离概率指标已不再适用。根据HDR以及概率值估计方法DQA,本文采用了适用于非线性、非高斯过程的广义概率指标(generalized local probability,GLP)
| ${\rm{GLP}}\left( {\mathit{x}_{\rm{t}}^{{\rm{monitor}}}} \right) = P\left( {f\left( \mathit{\boldsymbol{X}} \right) \ge f\left( {\mathit{\boldsymbol{x}}_{\rm{t}}^{{\rm{monitor}}}} \right)} \right) $ | (17) |
其中f (X)表示一维随机向量,由随机变量X的联合概率密度分布函数(probability density function,PDF)映射得到,xtmonitor表示当前监控数据。由n个样本观测数据x= (x1, x2, …, xd)T,可以得到n个联合概率密度函数值y = (y1, y2, …, yn),因此在某个置信水平下,对于监控数据xtmonitor,如果存在
| $q_{\hat \delta }^y = f\left( {\mathit{\boldsymbol{x}}_{\rm{t}}^{{\rm{monitor}}}} \right) $ | (18) |
则有
| ${\rm{GLP}}\left( {\mathit{\boldsymbol{x}}_{\rm{t}}^{{\rm{monitor}}}} \right) \cong 1 - \mathit{\hat \delta } $ | (19) |
DAQ方法得到的是区间估计,实际上通过对联合密度分布函数y的离散化处理,离散化步长为l,对应的得到一张包含l个区间的密度分位数表(包含l +1个置信水平和l+1个密度分位数值)。对于给定的控制线(CL∈(0, 1)),离散化步长为[1/(1-CL)]([]表示取整)。只要离散化步长足够大,对GLP的估计就可以设定为其所在概率估计区间上下界的均值,通过该方法可以实现GLP任意精度的估计。在控制线CL下,若GLP < CL,则认为过程是正常的,反之过程出现异常。
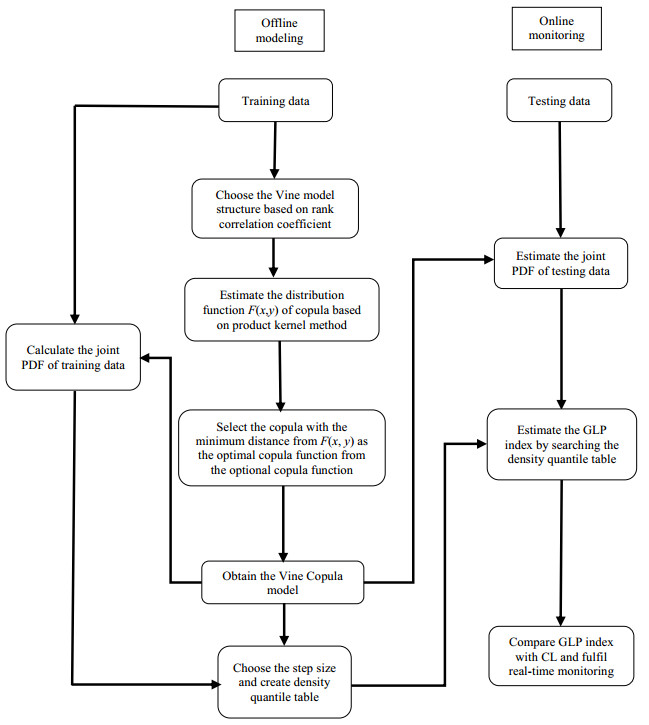
3.2 基于核密度估计的R-Vine模型的故障检测方法基于简化R-Vine模型的故障检测过程主要包括两个阶段:离线建模和在线监控,图(1)为整个过程的监测方法流程图,具体操作步骤如下:
离线建模:
(1) 获得正常操作状态下的训练样本集,利用(10)式得到各变量的边缘分布函数并确定变量间的秩相关系数;
(2) 利用最大生成树算法和秩相关系数确定树结构T;
(3) 根据(12)式利用乘积核的核密度来估计第一棵树中的第一个真实二元Copula分布函数值
(4) 计算每一个备选二元Copula函数和
(5) 其余的二元Copula函数操作步骤与(3),(4)一致,最终获得核密度估计下的最优R-Vine模型:
(6) 根据控制限CL确定离散化步长,利用获得的KRVC模型计算训练样本的联合概率密度函数值,从而构建过程的密度分位数表。
在线监控:
(1) 结合式(18)和(19),以查表的方式确定监控数据xt monitor的广义局部概率密度指标GLP(xt monitor);
(2) 在给定的控制限CL下,判断GLP指标是否超限。
|
图 1 KRVC过程监控方法流程图 Fig.1 Flow chart of the KRVC monitoring approach |
通过在TE过程和醋酸脱水过程中的的应用验证KRVC模型处理复杂变量的有效性。通过与有限元高斯混合模型FGMM、KPCA等传统方法的对比,表明KRVC方法在故障检测中的良好性能。
4.1 TE过程TE (Tennessee Eastman)过程是由美国Eastman公司根据实际的化工反应过程开发的测试仿真平台。该过程包括反应釜、冷凝器、压缩机、汽液分离器和汽提塔等5个主要操作单元。作为一个典型的复杂过程案例,TE过程广泛应用于故障检测与诊断等研究领域。TE过程包扩了22个连续的过程变量、19个成分变量和12个操纵变量以及21个故障信息。在本文的研究中选取了22个连续的过程变量建立KRVC模型,并对21个故障进行实时监测。TE过程仿真数据可从http://web.mit.edu/braatzgroup/links.html下载。
离线建模阶段,利用正常工况下的960组样本建立KRVC,KPCA和FGMM过程监控模型以作对比分析,为了保证对比的有效性和公平性,KPCA、FGMM方法分别取自相应文献[6, 14],模型参数设置也与原始文献一致,KPCA的窗宽50,选择高斯核函数,置信水平均设置为0.99。表 1给出了这3种方法的TE过程监控结果。每个故障的最优检测值用粗体表示。
|
|
表 1 TE过程21个故障的检测率(CL = 0.99) Table 1 Fault detection rates of 21 faults in the TE process (CL = 0.99) |
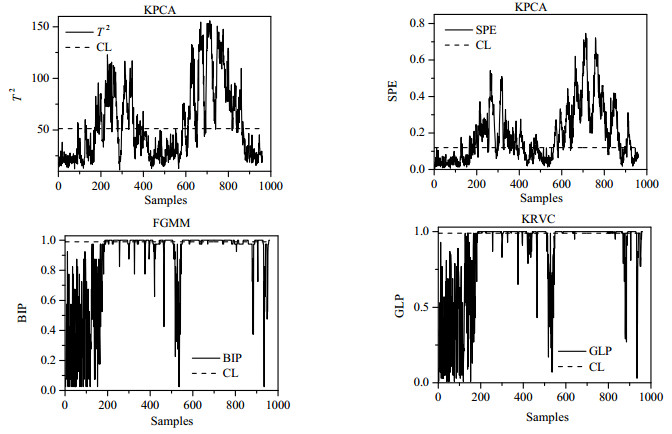
显而易见,在绝大多数故障类型上KRVC都能取得优于KPCA以及FGMM方法的检测结果。虽然KRVC未能在故障8,12,13和18上取得最佳的检测效果,但是相应的检测率差异是微乎其微的。对于故障3,4,5,15,19等,故障数据与正常状态下的数据差异细微,很难检测出来,因此这3种方法的检测效果都不是太理想。虽然3种方法的检测率都比较低,但是相比较而言,KRVC的检测率仍高于其他2种方法,尤其对故障19来说,以41.63检测率远高于KPCA和FGMM的16.13、10.88。为了直观地显示3种方法检测效果的差异,图 2为故障10的监控图。
|
图 2 故障10的过程监控图 Fig.2 Fault detection charts of Fault 10 during the TE process |
对于TE过程中具有非高斯态的数据,基于马氏距离的FGMM方法刻画数据异常点的能力显著降低;虽然KPCA方法增强了非线性处理的能力,但是仍然采取降维的思想,在数据变换和特征提取的过程中必然造成部分信息的损失。而KRVC方法以变量之间的相关性强弱建立树结构,在刻画非线性非高斯性方面有显著的优势,全面挖掘出数据变量之间的信息,同时基于核密度估计的R-Vine Copula选择方法为统计建模赋予了更强的灵活性,极大提高了故障检测的性能。
4.2 醋酸脱水过程精对苯二甲酸是纺织和包装行业广泛使用的聚酯生产的重要原料。它是由对二甲苯催化氧化生成的粗对二甲苯酸经过加氢、结晶、分离和干燥得到的,在氧化过程中醋酸是重要的的溶剂。通常在反应过程中部分醋酸会和水一起从反应器的顶部离开,而溶剂脱水塔则从废水中回收醋酸。当醋酸浓度较低时,醋酸和水的相对挥发度接近于1,很难用普通的精馏分离,为了降低能耗,工业上常采用共沸精镏法。加入共沸剂增加醋酸和水的相对挥发度,在正常情况下,蒸馏塔的上、下产品分别是水和醋酸。经过蒸馏分离操作后,顶部产品的醋酸含量一般低于1.15%,精馏得到的醋酸含水量在5%~8%,然后醋酸返回反应器。
醋酸脱水过程控制系统中有90级塔板和4个进料,乙酸和水的混合物来自氧化反应器。采用包括温度、压力、流量和电导率等连续的21个过程测量对顶部醋酸精馏过程进行实时监控。用于建模的500组训练数据和300组测试数据来自DCS。
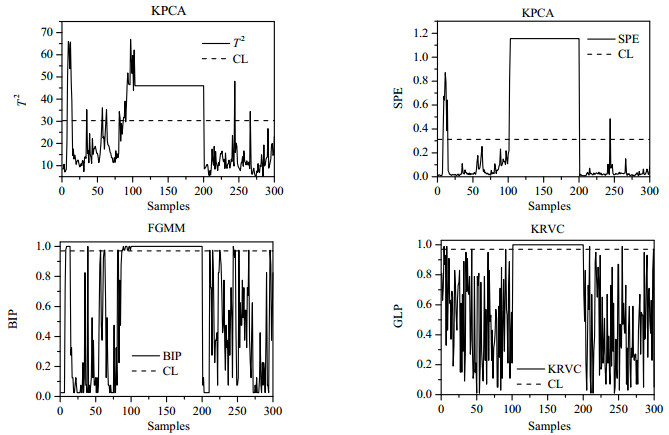
在离线建模阶段,利用500组训练数据建立KRVC模型。300组测试数据设置如下,前100时刻过程正常运行,在101时刻顶部产品醋酸含量由不到1.15%上升到1.5%,并持续100时刻,在最后的100时刻,醋酸含量又降到1.15%以下。表 2为KPCA、FGMM、和KRVC三种方法在控制限CL = 0.97下的检测率(fault detection rate,FDR)和误报率(fault positive rate,FPA),监控图如图 3所示。可以发现,不管是检测率还是误报率,KRVC方法都是最优的。表明本文提出的KRVC方法在醋酸脱水过程监控中有着很好的性能。
|
图 3 醋酸脱水过程的监控图 Fig.3 Monitoring results of the acetic acid dehydration process |
|
|
表 2 醋酸脱水过程的检测率和误报率(CL = 0.97) Table 2 Fault detection and false alarm rates of the acetic acid dehydration process(CL=0.97) |
本文提出一种基于KRVC模型的过程监控方法,在过程监控领域表现了优越的性能。KRVC方法利用变量之间的最强相依关系建立树结构,在此基础上采用核密度估计方法进行二元Copula函数的优化选择。该方法抛弃了数据处理的一般化降维和高斯假设思想,直接刻画变量之间的相关行为,全面挖掘出高维数据中复杂的相关性信息,获得更加精确的分布模型。根据HDR和DQA等理论构建了一类GLP指标,通过查询密度分位数表的形式实现对过程的实时监控。通过该方法在TE过程中以及醋酸脱水过程中的应用,表明与传统的KPCA、FGMM方法相比,KRVC监测方法具有更好的监控效果。
| [1] |
QIN S J. Survey on data-driven industrial process monitoring and diagnosis[J]. Annual Reviews in Control, 2012, 36(2): 220-234. DOI:10.1016/j.arcontrol.2012.09.004 |
| [2] |
GE Z. Review on data-driven modeling and monitoring for plant-wide industrial processes[J]. Chemometrics and Intelligent Laboratory Systems, 2017, 171: 16-25. DOI:10.1016/j.chemolab.2017.09.021 |
| [3] |
MS L H C, RUSSELL E L, BRAATZ R D. Fault detection and diagnosis in industrial systems[M]. London: Springer, 2001.
|
| [4] |
WOLD S, ESBENSEN K, GELADI P. Principal component analysis[J]. Chemometrics and Intelligent Laboratory Systems, 1987, 2(1): 37-52. |
| [5] |
MACGREGOR J F, JAECKLE C, KIPARISSIDES C, et al. Process monitoring and diagnosis by multiblock PLS methods[J]. AIChE Journal, 1994, 40(5): 826-838. DOI:10.1002/(ISSN)1547-5905 |
| [6] |
LEE J M, YOO C K, CHOI S W, et al. Nonlinear process monitoring using kernel principal component analysis[J]. Chemical Engineering Science, 2004, 59(1): 223-234. DOI:10.1016/j.ces.2003.09.012 |
| [7] |
KRAMER M A. Nonlinear principal component analysis using autoassociative neural networks[J]. AIChE Journal, 1991, 37(2): 233-243. DOI:10.1002/(ISSN)1547-5905 |
| [8] |
郭金玉, 王鑫, 李元. 基于加权差分主元分析的化工过程故障检测[J]. 高校化学工程学报, 2018, 32(1): 186-196. GUO J Y, WANG X, Li Y. Fault detection in chemical processes using weighted differential principal component analysis[J]. Journal of Chemical Engineering of Chinese Universities, 2018, 32(1): 186-196. |
| [9] |
ZHANG Y, HU Z. Multivariate process monitoring and analysis based on multi-scale KPLS[J]. Chemical Engineering Research and Design, 2011, 89(12): 2667-2678. DOI:10.1016/j.cherd.2011.05.005 |
| [10] |
徐欧官, 陈祥华. 移动窗递推PLS软测量建模及其工业应用[J]. 高校化学工程学报, 2009, 23(6): 1044-1050. XU O G, CHEN X H. Recursive PLS soft-sensor with moving window of fixed length and its commercial application[J]. Journal of Chemical Engineering of Chinese Universities, 2009, 23(6): 1044-1050. DOI:10.3321/j.issn:1003-9015.2009.06.024 |
| [11] |
KANO M, TANAKA S, HASEBE S. Monitoring independent components for fault detection[J]. AIChE Journal, 2003, 49(4): 969-976. DOI:10.1002/(ISSN)1547-5905 |
| [12] |
LEE J, YOO C, LEE I. Statistical process monitoring with independent component analysis[J]. Journal of Process Control, 2004, 14(5): 467-485. DOI:10.1016/j.jprocont.2003.09.004 |
| [13] |
GE Z Q, SONG Z H. Process monitoring based on independent component analysis-principal component analysis (ICA-PCA) and similarity factors[J]. Industrial & Engineering Chemistry Research, 2007, 46(7): 2054-2063. |
| [14] |
JIE Y U, QIN S J. Multimode process monitoring with Bayesian inference-based finite Gaussian mixture models[J]. AIChE Journal, 2008, 54(7): 1811-1829. DOI:10.1002/(ISSN)1547-5905 |
| [15] |
DISSMANN J, BRECHMANN E C, CZADO C, et al. Selecting and estimating regular Vine Copulae and application to financial returns[J]. Computational Statistics & Data Analysis, 2013, 59: 52-69. |
| [16] |
WEI Y, ZHANG S. Dependence analysis of finance markets:Copula-garch model and its application[J]. Systems Engineering, 2004, 4: 7-12. |
| [17] |
MADADGAR S, MORADKHANI H. Drought analysis under climate change using copula[J]. Journal of Hydrologic Engineering, 2011, 18(7): 746-759. |
| [18] |
JOE H. Families of m-variate distributions with given margins and m (m-1)/2 bivariate dependence parameters[J]. Distributions with Fixed Marginals & Related Topics Lecture Notesmonograph, 1996, 28: 120-141. |
| [19] |
REN X, TIAN Y, LI S J. Vine Copula-based dependence description for multivariate multimode process monitoring[J]. Industrial & Engineering Chemistry Research, 2015, 54(41): 10001-10019. |
| [20] |
ZHENG W, REN X, ZHOU N. Mixture of D-Vine Copulas for chemical process monitoring[J]. Chemometrics and Intelligent Laboratory Systems, 2017, 169: 19-34. DOI:10.1016/j.chemolab.2017.08.002 |
| [21] |
李霞. Copula方法及其应用[M]. 北京: 经济管理出版社, 2014. LI X. Copula method and its application[M]. Beijing: Economy & Management Publishing House, 2014. |
| [22] |
LINDSKOG F.Modelling dependence with Copulas and applications to risk management[D].Swiss: ETH Zürich, 2000.
|
| [23] |
SKLAR A. Fonctions dé Repartition á n Dimension et Leurs Marges[J]. Publications Del'Institut de Statistique de L'Université de Paris, 1959, 8: 229-231. |
| [24] |
BEDFORD T, COOKE R M. Probability density decomposition for conditionally dependent random variables modeled by Vines[J]. Annals of Mathematics and Artificial Intelligence, 2001, 32(1): 245-268. |
| [25] |
AAS K, CZADO C, FRIGESSI A. Pair-Copula constructions of multiple dependence[J]. Insurance Mathematics & Economics, 2009, 44(2): 182-198. |
| [26] |
KUROWICKA D, JOE H. Dependence modeling:Vine Copula handbook[M]. Singapore: World Scientific, 2011.
|
| [27] |
BRECHMANN E C, JOE H. Truncation of Vine Copulas using fit indices[J]. Journal of Multivariate Analysis, 2015, 138: 19-33. DOI:10.1016/j.jmva.2015.02.012 |
| [28] |
WANG W, WELLS M T. Model selection and semiparametric inference for bivariate failure-time data[J]. Journal of the American Statistical Association, 2000, 95(449): 62-72. DOI:10.1080/01621459.2000.10473899 |
| [29] |
RUDEMO M. Empirical choice of histograms and kernel density estimators[J]. Scandinavian Journal of Statistics, 1982, 65-78. |
| [30] |
HYNDMAN R J. Computing and graphing highest density regions[J]. Journal of the American Statistical Association, 1996, 50(2): 120-126. |
| [31] |
SAGARA S, ZHAO Z Y. Numerical integration approach to on-line identification of continuous-time systems[J]. Automatica, 1990, 26(1): 63-74. DOI:10.1016/0005-1098(90)90158-E |




