多喷嘴对置式水煤浆气化炉[1]由燃烧室和洗涤冷却室组成,燃烧室产生的高温粗合成气由竖直洗涤冷却管进入液池内。该过程中,冷却水沿洗涤冷却管内壁以液膜形式与高温粗合成气并流向下流动,液膜与高温合成气进行剧烈传质传热的同时也对洗涤冷却管起到保护作用。当液膜流量过小,进液量低于蒸发量,可能使洗涤冷却管壁面干壁,高温气体与壁面直接接触会损伤洗涤冷却管;而液膜流量过大,则过厚的液膜在轴向和周向上分布差异较大,难以保持稳定[2],使换热壁面受热不均产生变形。
有关壁面对液膜行为的影响,已有较为丰富的研究工作:朱业铭等[3]运用数值模拟方法研究了垂直多孔壁面孔径对液膜波动及其破裂特性的影响。结果表明:相较于光滑壁面,多孔板增强了气相与液相扰动,从而增强了液膜传质能力。王小明等[4]通过实验表明,对壁面使用倾斜刮板有助于液膜均匀分布。还有研究者尝试改进壁面物质构成,Kim等[5]与Cho等[6]对H2O/LiBr水平管进行降膜吸收实验,吸收效果得到明显提升。彭玉凤等[7]通过模拟实验表明,采用内部输水壁面能降低液膜厚度还能抑制液沫夹带现象。其实无论是对壁面进行结构优化还是改变壁面材料,目的都是给原来相对平稳的液膜增加扰动,使相间原本单一的分子扩散传质变为具有对流混流的高效传质,从而大幅提升传热效率。
关于降膜流动特性的研究,也有较丰富的研究工作:Chu等[8]在研究中定义了2种随机波:携有大量液体质量的大波以及填充在大波间起连接作用的衬底液膜上的小波,衬底液膜对热质传递效率的影响占主导作用。气相速度对大波的结构以及波动特性有决定性的影响[9]。Karimi等[10]对高湍动降膜过程中的大扰动波进行研究,结果表明大扰动波不一定携带较大液体质量。Drosos等[11]在研究中指出当液相雷诺数在一定界限内(ReL=200~400),ReL对液膜流动波形结构影响较弱。随着表征技术发展,Zadrazil等[12]应用光学激光测量技术(PLIF)对环状流液膜进行研究,提出气相进入流动的液相需要高度依赖液膜大振幅波的存在。尽管已有大量针对液膜的波动特性的研究,但大多只针对较低雷诺数(ReL < 5×103)的条件。而在洗涤冷却过程中液膜流动往往是剧烈高湍动的,但鲜有对强化扰动壁面上液膜波动特性的研究。因此开展针对高湍动条件下壁面结构对降膜流动波动特性影响的研究具有重要意义。本研究通过对降膜壁面结构进行设计改造,制作了3种不同结构参数的壁面,并借助超声多普勒测速仪(UDV) 研究了壁面结构参数对降膜流动特性的影响,为改善洗涤冷却过程液膜的质热传递效率提供一定的理论基础。
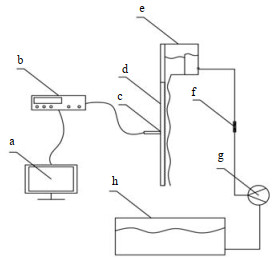
2 实验装置与方法 2.1 实验装置实验装置如图 1所示,装置以及降膜壁面由有机玻璃板制成。实验液相为水,从蓄水池经离心泵输送往装置进口处,流量大小由转子流量计调节,水在装置上部缓冲槽内积蓄,形成静水,而后经水箱底部宽度为4 mm的缝隙分布形成液膜,并沿着壁面向下流动,最终流入蓄水池内,由于装置上部水箱气密性良好,与大气压隔绝,所以水箱出口处液膜流量等于进口流量,即转子流量计流量。实验水温控制在(25±2) ℃。
|
图 1 实验设备装置图 Fig.1 Schematic diagram of experimental setup a. computer b. UDV c. transducer d. scrubbing cooling plate e. water tank f. flowmeter g. water pump h. reservoir |
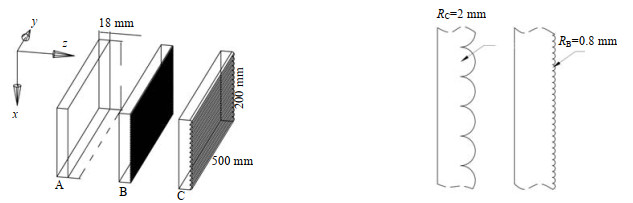
如图 2所示,条纹壁面B、C由多个截面为半圆形的柱体覆盖构成,通过改变柱状条纹截面半径(R,mm)来改变壁面扰动强度;实验过程使用壁面A(光滑壁面);壁面B(RB=0.8 mm);壁面C(RC=2.0 mm)。x为液膜下降方向,即轴向,y为壁面宽度方向,z为垂直于壁面方向。壁面A、B和C的高度均为200 mm,宽度均为500 mm。定义液膜在降膜壁面的进口位置x= 0 mm,出口位置x= 200 mm。
|
图 2 洗涤冷却壁面结构示意图 Fig.2 Geometric structure of scrubbing-cooling plates |
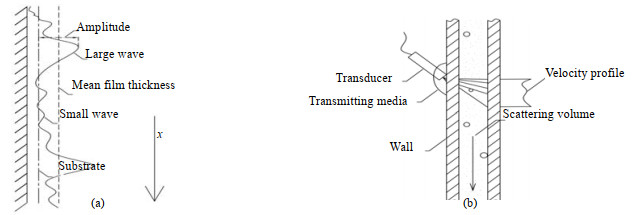
采用UDV对降液膜的厚度和轴向速度进行测量,其测量原理如图 3所示。探测器向液膜发射一定频率的声波。声波与流体所成夹角即多普勒角。声波在流体中传播,遇到流体中夹带的气泡或其他微粒时即被反射,产生的反射波频率也发生改变,这就是多普勒效应。Fischer等[13]与Jaafar等[14]在研究中利用动态频谱和信号分析相关计算,得到了在声波传播途径中流体中不同位置流体质点速度图谱,不同位置粒子产生的反射波被探测器接收时间不同,由信号动态频谱分析计算,可以得到声波传播路径上不同位置微粒的速度,可以将该速度视为该位置的流体速度。超声波经由壁面与液膜的固液界面进入流体,再经液膜与空气间的气液相界面进入空气,声波经过这类相界面时会产生反射波,被探测器接收。声波经过两个相界面产生的反射波存在一定的时间差,结合声波在相应条件下的传播速度可以得到两相界面间的厚度,即为液膜厚度。Li等[15]与Jayakumar等[16]在研究中证明了该方法的可靠性。本研究采用的声波频率为4 MHz,液膜厚度测量的空间分辨率为0.12 mm,数据采集频率为100次⋅s−1,测量液膜厚度时探测器与壁面垂直,测速时探测器与壁面夹角(多普勒角)为85°。
|
图 3 液膜波动类型及UDV原理示意 Fig.3 Falling film and principle of UDV measurement |
实验通过控制转子流量计调节流量大小,并通过缓冲槽和折流板使成膜速度稳定,进而准确地控制液体流动的ReL大小。在不同ReL条件下,分别在x=20~180 mm处每隔20 mm设置一个测量点,在每个测量点用UDV测量液膜的厚度和速度数据。
液膜雷诺数定义为
| $ R{e_{\rm L}}=\frac{{4\varGamma }}{\mu } $ | (1) |
式中:Γ为液膜单位湿周上的质量流率,kg⋅s−1;μ为水的黏度,Pa⋅s。
2.5 误差分析声速误差:通过NIST获得在UDV测试时使用的声速参数,同时该参数的设置根据实际的液膜温度来加以修正,将此方法下UDV测出的实际声速记为VM,NIST声速记为VN。则水中的声速误差为
| $ {E_{\rm s}}=\frac{{|{V_{\rm N} }- {V_{\rm M}}|}}{{{V_{\rm M}}}} $ | (2) |
式中:VN为通过美国国家标准及技术研究所(NIST)获得的水的声速,m⋅s−1;VM为本实验通过UDV测量的水的声速,m⋅s−1。本研究中最大的声速误差为0.49%。
液膜厚度测量误差:本实验利用数码相机拍摄净水高清图像,利用图像处理软件ImageJ得到净水的真实高度记为hT(m),将UDV测得的水高记为hM(m)。则将液膜厚度测量的误差定义为
| $ {E_\delta }=\frac{{|{h_{\rm M}} - {h_{\rm T}}|}}{{{h_{\rm T}}}} $ | (3) |
本研究液膜厚度测量最大误差为0.53%。
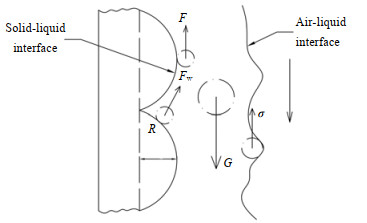
2.6 液膜受力分析为了便于研究降膜的流动特性,对降膜过程中液体受到的主要作用力进行分析,如图 4所示;F为液体受到来自壁面的剪切应力,N;Fw为壁面凸起结构给下降液膜带来的阻力,N;G为重力,N;σ为液膜表面张力,N⋅m−1。本实验降膜高度仅为200 mm,且在空气静止的室内完成,可以忽略气液界面阻力的影响。对于平滑壁面上湍流的垂直降膜,重力与壁面的剪切力是主要的作用力[17-18]。
|
图 4 液膜受力分析 Fig.4 Force analysis of liquid film |
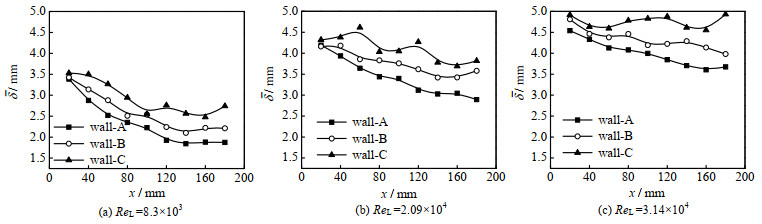
液膜平均厚度δ (mm)的轴向分布和波动特性对质热传递有显著影响,在ReL=8.3×103 ~ 3.14×104的条件下,壁面A、B和C的平均液膜厚度轴向分布如图 5所示。
|
图 5 不同雷诺数下液膜平均厚度随壁面扰动变化曲线 Fig.5 Variation of mean thickness of liquid film with wall disturbance under different Reynolds numbers |
由图 5可知,随着ReL增加,各轴向位置处的平均液膜厚度曲线“上移”。这表明ReL的增加整体上促进了液膜厚度的增大,这是由于随着ReL增加,液膜湍动程度愈剧烈,使得液膜波幅增加且波周期缩短[19],从而导致瞬时厚度较大的液膜产生,并且促进了衬底液膜增厚[17]。这也印证了液膜平均厚度与ReL的正相关性[20]。如图 5所示,在3种ReL条件下,在光滑壁面A上的液膜厚度均随着流动方向不断减小。这是由于在轴向方向上,液膜在重力作用下产生了前后速度差,在这种前后速度差的“拉伸”之下,液膜逐渐变薄。而壁面B、C上的液膜厚度不再单一地随着轴向距离增加而变薄,而是总体下降的大趋势下呈现上下起伏的变化趋势,这表示液膜受力状况更复杂了,这一现象将在3.2节更深入地分析。
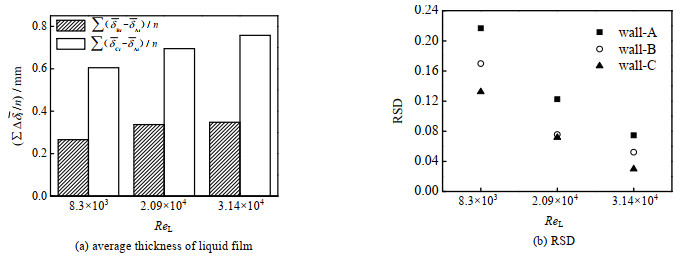
同一ReL条件下,从壁面A到壁面C,平均厚度曲线上移,表明壁面结构扰动使液膜平均厚度变厚, 为了更直观地观察液膜变厚的程度,在各ReL条件下,分别计算出壁面B、C与壁面A上各个x处的平均液膜厚度的差平均值
|
图 6 液膜平均厚度增厚程度与RSD Fig.6 Thickening degree of average liquid film thickness and RSD |
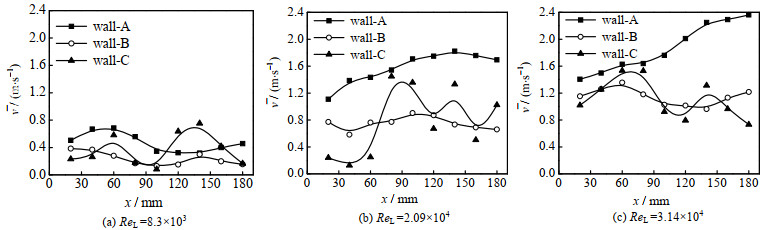
为了更全面了解液膜轴向运动,在各测量点10 s内取1 000次液膜速度,取平均值得到液膜轴向平均速度v (m⋅s−1),如图 7所示。
|
图 7 不同雷诺数下液膜平均速度随壁面扰动变化曲线 Fig.7 Variation in average velocity of liquid film on the wall under different Reynolds numbers |
图 7反映了ReL=8.3×103 ~ 3.14×104情况下各壁面上液膜轴向平均速度随x变化曲线。对于光滑壁面A,在ReL=8.3×103情况下,平均速度曲线呈现起伏变化,平均速度在x=60 mm处达到极大值(0.685 m⋅s−1),然后变小;到x=140 mm处达到极小值(0.31 m⋅s−1),然后开始增大。重力是降膜过程的向下驱动力,表明在x=60与140 mm处液膜所受合力方向(即加速度方向)发生了改变。结合3.1节中分析可知,ReL=8.3×103时壁面A上的液膜平均厚度最低,即单位面积液膜所受重力较弱,当膜厚较低时壁面剪切力F则可能大于单位面积液膜所受重力[21],表面张力σ是物质特性不受膜厚影响;当重力与各阻力项之和的大小关系发生了变化,液膜加速度方向也随之改变,导致平均速度曲线的波动。而随着ReL增大,液膜厚度增加,单位面积液膜所受重力增加,平均速度整体上随x单调增大,表明液膜加速度即所受合力向下。
对于壁面B、C上的平均速度曲线,均呈波动变化,并且平均速度曲线在壁面C上波动较壁面B更为剧烈,表明液膜受力较平滑壁面A更为复杂。一方面壁面结构的改变使重力在x方向的分力发生变化,影响了液膜速度曲线波动[22]。尽管壁面B、C上液膜厚度变大,但由于壁面B、C较壁面A对液膜受力多了Fw阻力项,使得重力与各阻力项之和的大小关系更复杂,从而使平均速度波动更为剧烈,这种速度波动利于液膜自身的传质。与平均厚度的波动相似,可以观察到这种平均速度的波动也受到ReL的影响。
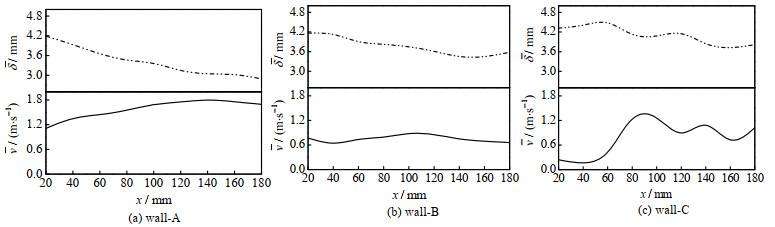
为探究平均速度波动与平均厚度波动的关系,将速度与厚度直接比对,结果如图 8所示。取ReL=2.09×104情况下各壁面上液膜平均速度与平均厚度随下降高度的变化曲线进行直接比对。从图中可以看出,壁面A上,液膜运动的平均速度与平均厚度呈现明显的负相关,随着液膜速度的增大,液膜厚度不断减小,这表明正是在液膜加速度的作用下,不同x位置的液膜之间产生了速度差,这种前后的速度差异使得液膜变薄,验证了3.1节中的论述。
|
图 8 不同壁面液膜平均速度与平均厚度曲线对比 Fig.8 Comparison of average velocity and average liquid film thickness on the wall |
对于壁面B,厚度与速度曲线也存在着局部的负相关,如图 8(b)所示,在x < 40 mm处,伴随着液膜速度下降,液膜厚度也有一定的上升(约从4.16至4.17 mm);然后随着液膜速度增大(在x=100~120 mm达到极大值),液膜厚度开始减小(约在x=140 mm处达到极小值)。这是由于液膜的减速过程中,x方向上,前方液膜速度大于后方,后方液体对前方及时进行了补充,液膜因此增厚。反之液膜加速过程中,前方的液膜速度大于后方,这种加速作用使得液膜变薄。
同时,由于加速度方向的改变使液膜速度变化再到使液膜厚度变化的过程并不是同时发生的,二者存在时间的先后差异,这个过程液膜仍在向x方向运动,所以厚度曲线与速度曲线的极值点并不严格位于同一x处。对于壁面C,如图 8(c)所示,由于R的增大,Fw对液膜的作用更为强烈,液膜速度曲线波动也较壁面B更为剧烈。在x=20~180 mm处,厚度曲线的极值点增多至4个,速度曲线极值点增多至5个。这种速度波动有利于液体间传质进而促进传热[23],利于液膜均匀受热。
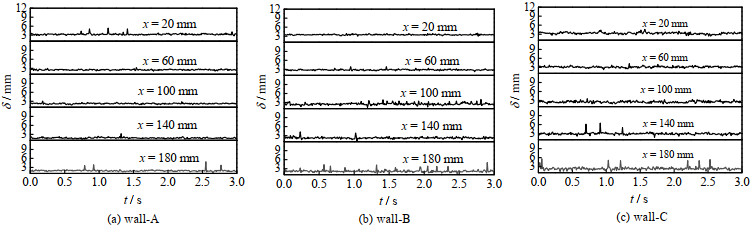
3.3 瞬时厚度分布为更直观体现液膜瞬时厚度空间分布状况以及大波出现概率,在液膜运动状况稳定情况下任意取3 s内300个瞬时液膜厚度δ (mm)数据,如图 9所示。t为时间(s),在ReL=8.3×103时,分别为液膜在壁面A、B、C上瞬时厚度分布情况。可以看到,该ReL情况下光滑壁面A的液膜瞬时厚度相对稳定,当下降高度到达一定程度后,出现一定概率波动。相比之下壁面B与C在同样的下降高度,液膜瞬时厚度相对不稳定,大波出现概率增大。对比壁面A,壁面B、C的壁面结构会给液膜流动增强扰动,使得液膜厚度更不稳定,液膜厚度出现了一定程度的波动。
|
图 9 ReL=8.3×103时各壁面上液膜瞬时厚度分布 Fig.9 Instantaneous thickness distribution of liquid film on the wall when ReL=8.3×103 |
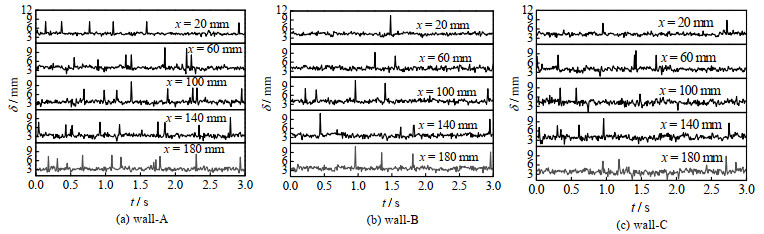
在ReL=3.14×104时,如图 10所示,光滑壁面A出现较高频率的高瞬时液膜厚度,表明液膜大波出现概率较大,同时观察到x > 100 mm后,这种大波出现频率又随着轴向距离增加而降低[24]。对比之下,液膜在壁面B、C上也出现了一定概率的大波动,但比壁面A出现概率明显降低,如图 10(b)、(c)所示,而大波本身不利于传热[19]。结合3.2节中分析,这是由于壁面B与C给液膜带来了Fw阻力项,液膜速度波动更为剧烈,使大波破裂[25]。而壁面B上的液膜出现大波动的概率又相较于壁面C更低,这可能是由于壁面C的结构更大程度增强了液膜的扰动,使得液膜产生了较大的Z方向上的厚度波动;同时发现,壁面C上的液膜出现了明显低于平均厚度的瞬时厚度波动,如x=180 mm处,出现液膜瞬时厚度最低可达1.37 mm(此处的平均液膜厚度为4.93 mm),这可能是由于壁面的凸起处使液膜变薄,甚至液膜产生破裂[26]。当下降高度较大时,使液膜出现断层的概率增大,这种情况在实际生产过程中是不被允许的。而壁面B的表面结构条纹相对细而密,有效地避免了这种情况的发生,同时又能一定程度维持液膜的相对稳定。
|
图 10 ReL=3.14×104时各壁面上液膜瞬时厚度分布 Fig.10 Instantaneous thickness distribution of liquid film on the wall when ReL=3.14×104 |
本研究利用核函数(Ksdensity)对瞬时液膜厚度分布的概率密度函数(PDF)拟合。瞬时厚度空间分布图可以看到较大的液膜波动,也就是大波出现概率,而PDF曲线则可以更直观地观察到衬底液膜波动情况。由于拟合过程会将接近于0的正数据做自动处理,导致PDF曲线出现负值。因此本研究利用反射法对边界进行校正,使得边界附近不会出现多余的峰值。
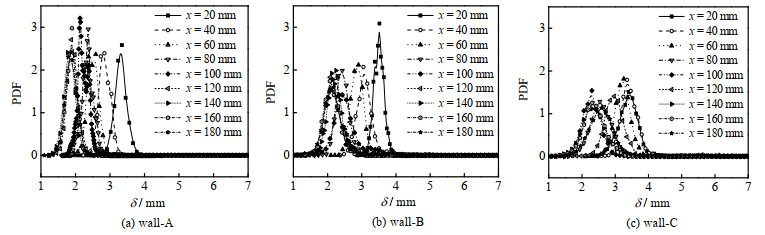
在ReL=8.3×103时,壁面A、B和C的PDF曲线如图 11所示。对于光滑壁面A,PDF曲线峰在x=80 ~ 100 mm处时最为陡峭,这表明壁面A上的液膜在此处波动较小。其次对于壁面A与B的PDF曲线之间比较,可以发现在下降方向x=20 mm处,壁面B的PDF曲线要较壁面A更为陡峭,这表明该ReL条件下,一定程度的壁面扰动有利于下降初期衬底液膜流动的稳定。
|
图 11 ReL=8.3×103时各壁面不同下降高度PDF曲线 Fig.11 PDF distribution of instantaneous liquid film thickness on the wall when ReL=8.3×103 |
同时观察到,随着轴向距离增加,PDF曲线峰逐渐向左移动,这表明随着液膜的运动,低厚度液膜出现概率逐渐增高,这主要是平均液膜厚度逐渐降低的原因。对比图 11(a)、(b)和(c)可以发现:随着壁面结构扰动增强,相同x处PDF曲线峰值右移且更平缓,这表明液膜厚度随着壁面结构扰动强度而增厚,并且液膜湍动程度更强,这有利于液膜的传热[27]。结合图 11(a)、(b)、(c)可以看到光滑壁面A的PDF曲线总体上要相较壁面B、C更为陡峭,表明衬底液膜在光滑壁面上更为稳定。结合3.3节中的分析可知,壁面结构扰动降低了大波出现的概率,因为大波易破裂,其存在需要较为稳定的衬底液膜[8]。但壁面结构扰动增强了衬底液膜上小波的波动,正是小波更频繁的波动使得壁面B与C上的PDF曲线峰看起来更为平缓,而衬底液膜上小波的波动更利于传热[19]。
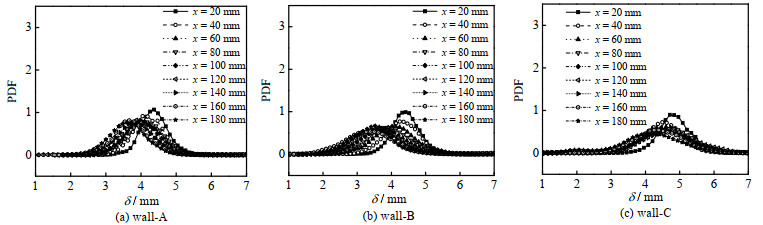
流量进一步增大至ReL=3.14×104,这时候一方面PDF曲线整体右移更为明显,如图 12所示;这表明ReL增大,液膜厚度明显增大。另一方面,PDF曲线整体变得更为平缓,峰的范围更加宽了,这意味着ReL的增大给液膜厚度带来更频繁的波动。而过于强烈的壁面扰动,使得液膜表面剧烈湍动,大波易破碎成液滴[28],同时加剧了衬底液膜上小波的波动,这也使得壁面A到壁面C上的PDF曲线逐渐变得更加平缓。同时观察到相同ReL情况下,随着壁面波动程度加强,不同下降高度处的PDF曲线峰值越加接近,这进一步表明,壁面扰动增强有助于维持x方向上的衬底液膜厚度均匀。
|
图 12 ReL=3.14×104时各壁面不同下降高度PDF曲线 Fig.12 PDF distribution of instantaneous liquid film thickness on the wall when ReL=3.14×104 |
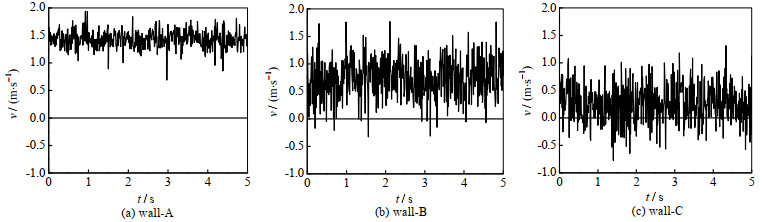
为了更深入地了解同一x处液膜速度的变化情况,在各壁面上同一x处5 s内取500个液膜瞬时速度ν(m⋅s−1)数据,如图 13所示。因为在同一ReL条件下,各x处展现出的瞬时速度分布随壁面变化趋势大致相同,所以取ReL=2.09×104时x=100 mm处各壁面上液膜速度曲线为例。由图 13可以看到,壁面的扰动会使得液膜速度波动明显加剧,其次速度曲线整体下移,表明壁面的结构扰动使得液膜速度减小,再次印证了前文的论述。同时可以观察到,随着壁面波动程度加强,会出现小于0的负方向速度,且波动程度最强的壁面C上出现负速度的现象最为明显,这可能是由于壁面的凹陷结构在液膜快速经过时,形成了负压区,一定条件下会使得液体回流,这部分回流的液体被监测到从而形成了负方向速度。
|
图 13 ReL=2.09×104不同壁面上液膜瞬时速度曲线 Fig.13 Instantaneous velocity of liquid film on the wall when ReL=2.09×104 |
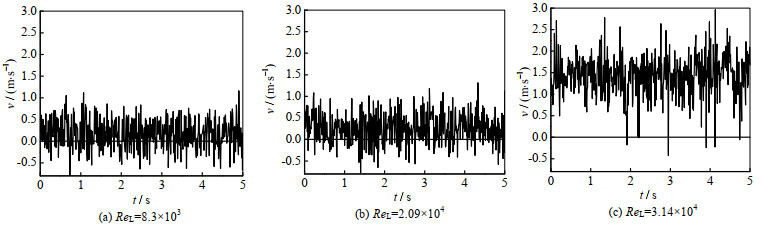
如图 14所示,壁面C在同一轴向位置处,不同ReL情况下瞬时速度曲线;可以看到随着ReL增大,速度曲线整体上移,同时曲线波动更为剧烈,这表明ReL增大,液膜运动速度增大,湍动程度加强。此外可以观察到随着ReL增大,负方向速度出现的概率降低。这表明在较大的质量流量情况下,回流的现象相对减弱,或者说回流流体质量占比降低,使得负方向速度出现频次降低。
|
图 14 壁面C上液膜瞬时速度随雷诺数变化曲线 Fig.14 Instantaneous velocity of liquid film on wall C under different Reynolds number |
(1) 湍动情况下,与光滑降膜壁面A相比较,具有更复杂的扰动结构壁面B与C使得液膜厚度明显增厚,壁面B平均最大增厚0.348 mm,壁面C最大增厚0.758 mm。同时有效地维持了轴向方向上液膜厚度均匀,在ReL=3.14×104条件下壁面C上的平均液膜厚度RSD达到最低0.027,而壁面A为0.075。
(2) 分析了液膜平均厚度与平均速度相互间影响的理论机制,壁面A上液膜速度与厚度呈明显的负相关性。壁面B、C上,液膜的平均速度与厚度曲线呈波动状,厚度与速度局部呈负相关性。由壁面B到壁面C,厚度与速度曲线波动更强烈,在x=20 ~ 180 mm内,厚度曲线极值点由2个增大至4个,速度极值点由2个增至5个,且厚度与速度曲线极值点并不严格相等。
(3) 对液膜瞬时厚度的空间分布分析可知,相比于光滑壁面A,壁面B与C的复杂壁面结构减少了大波出现的概率,这在ReL=2.09×104 ~ 3.14×104时更为明显;而同时壁面C产生了明显小于平均厚度的瞬时厚度波动,最低处可达1.37 mm,较该处平均厚度低3.56 mm。
(4) 通过分析瞬时液膜厚度分布的概率密度函数,发现条纹壁面结构扰动使PDF曲线明显右移,且使得曲线峰更加平缓。即使得液膜增厚的同时,也使得液膜的波动更加剧烈,利于传热。
(5) 分析液膜的瞬时速度分布发现,复杂的壁面结构会使降膜过程产生一定的回流现象,这种回流现象在壁面C上要强于壁面B,同时这种现象会随着ReL增大而减弱。该回流现象对液膜的质热传递效率有何影响需要进一步研究。
| [1] |
王辅臣, 代正华. 煤气化-煤炭高效清洁利用的核心技术[J]. 化学世界, 2015, 56(1): 51-55. WANG F C, DAI Z H. Coal gasification-core technology of coal efficient and clean utilization[J]. Chemical World, 2015, 56(1): 51-55. |
| [2] |
YAN L C, WANG Y F, WU Z W, et al. Research of vertical falling film behavior in scrubbing-cooling tube[J]. Chemical Engineering Research and Design, 2017, 117: 627-636. DOI:10.1016/j.cherd.2016.11.010 |
| [3] |
朱业铭, 刘金平, 许雄文, 等. 竖直多孔平板上液膜流动特性的研究[J]. 化工学报, 2021, 72(8): 4081-4092. ZHU Y M, LIU J P, XU X W, et al. Research on liquid film flow characteristics of vertical porous plate[J]. CIESC Journal, 2021, 72(8): 4081-4092. |
| [4] |
王小明, 许松林, 徐畅. 分子蒸馏装置中刮膜器对液膜流动状况的影响研究[J]. 高校化学工程学报, 2012, 26(1): 13-18. WANG X M, XU S L, XU C. Study on the effect of wiper Structure on the liquid film flow condition in wiped film molecular distillation apparatus[J]. Journal of Chemical Engineering of Chinese Universities, 2012, 26(1): 13-18. |
| [5] |
KIM J K, PARK C W, KANG Y T. The effect of micro-scale surface treatment on heat and mass transfer performance for a falling film H2O/LiBr absorber[J]. International Journal of Refrigeration, 2003, 26(5): 575-585. DOI:10.1016/S0140-7007(02)00147-0 |
| [6] |
PARK C W, CHO H C, KANG Y T, et al. The effect of heat transfer additive and surface roughness of micro-scale hatched tubes on absorption performance[J]. International Journal of Refrigeration, 2004, 27(3): 264-270. DOI:10.1016/j.ijrefrig.2003.09.008 |
| [7] |
彭玉凤, 陈倬, 朱家骅, 等. 内部输水性壁面波形除雾器性能研究[J]. 高校化学工程学报, 2021, 35(6): 979-985. PENG Y F, CHEN Z, ZHU J H, et al. Study on wave-plate demister with internal transport wall[J]. Journal of Chemical Engineering of Chinese Universities, 2021, 35(6): 979-985. |
| [8] |
CHU K J, DUKLER A E. Statistical characteristics of thin, wavy films: Part Ⅱ. Studies of the substrate and its wave structure.[J]. AIChE Journal, 1974, 20(4): 695-706. DOI:10.1002/aic.690200410 |
| [9] |
孙宏军, 王伟, 桂明洋. 水平管环状流液膜厚度与波动参数分布[J]. 化工学报, 2019, 70(11): 4162-4171. SUN H J, WANG W, GUI M Y. Distribution of liquid film thickness and wave parameters in horizontal annular flow[J]. CIESC Journal, 2019, 70(11): 4162-4171. |
| [10] |
KARIMI G, KAWAJI M. An experimental study of freely falling films in a vertical tube[J]. Chemical Engineering Science, 1998, 53(20): 3501-3512. DOI:10.1016/S0009-2509(98)00159-6 |
| [11] |
DROSOS E I P, PARAS S V, KARABELAS A J. Characteristics of developing free falling films at intermediate Reynolds and high Kapitza numbers[J]. International Journal of Multiphase Flow, 2004, 30(8): 853-876. |
| [12] |
ZADRAZIL I, MATAR O K, MARKIDES C N. An experimental characterization of downwards gas-liquid annular flow by laser-induced fluorescence: Flow regimes and film statistics[J]. International Journal of Multiphase Flow, 2014, 60: 87-102. DOI:10.1016/j.ijmultiphaseflow.2013.11.008 |
| [13] |
FISCHER S, SCHMITT P, ENSMINGER D, et al. A new velocity estimation method using spectral identification of noise[J]. Flow Measurement and Instrumentation, 2008, 19(3/4): 197-203. |
| [14] |
JAAFAR W, FISCHER S, BEKKOUR K. Velocity and turbulence measurements by ultrasound pulse Doppler velocimetry[J]. Measurement, 2009, 42(2): 175-182. DOI:10.1016/j.measurement.2008.05.004 |
| [15] |
LI F C, SERIZAWA A. Experimental study on flow characteristics of a vertically falling film flow of liquid metal NaK in a transverse magnetic field[J]. Fusion Engineering and Design, 2004, 70(2): 185-199. DOI:10.1016/j.fusengdes.2003.11.004 |
| [16] |
JAYAKUMAR A, BALACHANDRAN A, MANI A, et al. Falling film thickness measurement using air-coupled ultrasonic transducer[J]. Experimental Thermal and Fluid Science, 2019, 109: 109906. |
| [17] |
MASCARENHAS N, MUDAWAR I. Investigation of eddy diffusivity and heat transfer coefficient for free-falling turbulent liquid films subjected to sensible heating[J]. International Journal of Heat and Mass Transfer, 2013, 64: 647-660. |
| [18] |
MAROTEAUX F, LLORY D, LE COZ J F, et al. Liquid film atomization on wall edges — Separation criterion and droplets formation model[J]. Journal of Fluids Engineering, 2002, 124(3): 565-575. |
| [19] |
MASCARENHAS N, MUDAWAR I. Study of the influence of interfacial waves on heat transfer in turbulent falling films[J]. International Journal of Heat and Mass Transfer, 2013, 67: 1106-1121. |
| [20] |
WANG B, TIAN R F. Investigation on flow and breakdown characteristics of water film on vertical corrugated plate wall[J]. Annals of Nuclear Energy, 2019, 127: 120-129. |
| [21] |
WASDEN F K, DUKLER A E. Insights into the hydrodynamics of free falling wavy films[J]. AIChE Journal, 1989, 35(2): 187-195. |
| [22] |
马学虎, 薄守石, 兰忠, 等. 降液膜波动的影响因素分析[J]. 高校化学工程学报, 2010, 24(1): 10-15. MA X H, BO S S, LAN Z, et al. Analysis on wave flow of laminar-wavy falling liquid film[J]. Journal of Chemical Engineering of Chinese Universities, 2010, 24(1): 10-15. |
| [23] |
YU L M, ZENG A W, YU K T. Effect of interfacial velocity fluctuations on the enhancement of the mass-transfer process in falling-film flow[J]. Industrial & Engineering Chemistry Research, 2006, 45(3): 1201-1210. |
| [24] |
位宗瑶, 王亦飞, 颜留成, 等. 高雷诺数下管内垂直降膜瞬时厚度空间分布及波动特性[J]. 高校化学工程学报, 2018, 32(6): 1255-1263. WEI Z Y, WANG Y F, YAN L C, et al. Spatial distribution and wave characteristics of falling liquid film in scrubbing-cooling tube under high Reynolds numbers[J]. Journal of Chemical Engineering of Chinese Universities, 2018, 32(6): 1255-1263. |
| [25] |
ZENG J, WANG Y F, WEI Z Y, et al. Thickness distribution and fluctuation characteristics of liquid falling film under turbulent conditions[J]. Chemical Engineering Science, 2022, 248: 117-172. |
| [26] |
SINAI Y L. A model of interfacial stress and spray generation by gas flowing over a deep, wavy pool[J]. Journal of Fluid Mechanics, 1987, 179: 327-344. |
| [27] |
WEI Z Y, WANG Y F, WU Z W, et al. Wave characteristics of the falling liquid film in the development region at high Reynolds numbers[J]. Chemical Engineering Science, 2020, 215: 115454. |
| [28] |
LI X S, PAN H J, DONG X, et al. Spray impingement wall film breakup by wave entrainment[J]. Proceedings of the Combustion Institute, 2019, 37(3): 3287-3294. |




