 耗散数的绝热型溶液除湿/再生器性能预测解析模型
耗散数的绝热型溶液除湿/再生器性能预测解析模型
 Eh概念,导出焓
Eh概念,导出焓 耗散数Eh*,研究Eh*和等效热容比C*、焓效率εh及传热单元数(NTU)的变化关系,同时建立基于Eh*的顺/逆流除湿/再生器性能预测解析模型,分析Eh*对装置性能的影响。结果表明,Eh*与εh近似呈负线性关系,且随C*减小而逐渐增大,随NTU变大逐渐减少趋于稳定;当Eh*较小时,除湿/再生程度更深,而当Eh*趋近于1时,除湿/再生的热质传递趋于停止;在相同Eh*下,溶液进口温度和流量比对装置性能影响更大。
耗散数Eh*,研究Eh*和等效热容比C*、焓效率εh及传热单元数(NTU)的变化关系,同时建立基于Eh*的顺/逆流除湿/再生器性能预测解析模型,分析Eh*对装置性能的影响。结果表明,Eh*与εh近似呈负线性关系,且随C*减小而逐渐增大,随NTU变大逐渐减少趋于稳定;当Eh*较小时,除湿/再生程度更深,而当Eh*趋近于1时,除湿/再生的热质传递趋于停止;在相同Eh*下,溶液进口温度和流量比对装置性能影响更大。 解析模型 不可逆性 传热传质
解析模型 不可逆性 传热传质 溶液除湿是一种利用表面水蒸气分压力较低的水溶液吸收空气中水分的除湿方法,由于驱动能源品味要求低[1-3]、可以改善室内空气品质[4]等优势被研究人员所关注。在除湿过程中,吸湿性溶液与湿空气直接接触进行水分与热量的传递[5],因此溶液除湿过程是一个传热与传质相耦合的过程[6-8],给除湿/再生器数学模型建立及求解造成困难。
Lazzarin等[9]分析并建立了绝热型填料塔内空气与溶液之间传热传质的一维模型。代彦军等[10]建立除湿/再生器内叉流降膜除湿的传热传质过程数学模型。Varela等[11]通过雷诺-普朗特数和雷诺-施密特数给出溶液除湿/再生过程中传热传质的一般关系式。Ren等[12]在常见的溶液除湿/再生工况下将溶液平衡湿度比与温度的关系进行线性逼近。Babakhani等[13]给出可以预测各种变量在再生器内分布情况的解析解。Zhang等[14]基于传质单元数(NTUm)模型分析了热泵驱动的溶液除湿系统性能。Liu等[15]在NTUm的基础上提出用效率表示的除湿/再生器解析模型。上述研究从传热传质角度发展了除湿/再生器数学模型,但皆未从装置不可逆性的角度进行建模,无法分析装置不可逆性程度对除湿/再生器性能影响。
为了研究溶液除湿系统的不可逆损失,学者们从㶲效率的角度对溶液除湿系统进行分析[16-18]。然而类似于卡诺循环中㶲损趋于最小时,系统输出的功率趋于零,可逆理想除湿过程的㶲损趋于零时,除湿率也同样趋于零[19],难以指导工程实际的应用。基于此,Guo等[20]通过类比电势提出用于表征热势的物理量——











鉴此,本研究提出了焓




Guo等[20, 24-25]通过热电比拟提出温度
| $ {E_T} = \frac{1}{2}{Q_m}T $ | (1) |
式中:Qm=mcVT,m为物体质量,kg;cV为物体的比定容热容,kJ·kg−1·K−1;T为热力学温度,K;Qm为物体所含的热能,kJ。
ET这个物理量具有热势能的含义,也即物体传热能力的大小。在传热过程中,温度


在水与空气的质量交换中,江亿等[27]从传湿的角度出发,定义湿空气的湿
| $ {E_{{\text{a, w}}}} = \frac{1}{2}{q_{m{\text{, a}}}}w_{\text{a}}^2 $ | (2) |
式中:qm, a为干空气的质量流量,kg·s−1;wa为湿空气中水蒸气与干空气的质量比。
对于溶液与空气之间的传热传质过程,由于质量传递与热量传递间的相互影响较大,难以作为单纯的传热或传质过程进行分析,因此有必要找出同时包含温度和湿量的表达方式,而焓正是这样一个物理量,且溶液等效焓与空气焓之间的差值是溶液除湿/再生过程的一个独立驱动势[28],表征两流体间全热换热的动力,因此定义一个焓

对于质量流量为qm, a的干空气类比于温度

| $ {\text{d}}{E_{{\text{a, }}h}} = {q_{m, {\text{a}}}}{h_{\text{a}}}{\text{d}}{h_{\text{a}}} $ | (3) |
式中:ha为湿空气的比焓,kJ·kg−1;dha表示ha的微小变化量,kJ·kg−1。将式(3)进行积分可得湿空气的焓
| $ {E_{{\text{a, }}h}} = \frac{1}{2}{q_{m{\text{, a}}}}h_{\text{a}}^2 $ | (4) |
由于溶液和空气间的焓势在溶液侧表现为与溶液平衡的等效空气焓,并且基于该等效焓而产生的溶液和空气焓差是溶液本身焓变的驱动力,将溶液焓
| $ {\text{d}}{E_{{\text{s, }}h}} = q_{m{{\text{, s}}}}{h_{{\text{eq}}}}{\text{d}}{h_{\text{s}}} $ | (5) |
式中:qm, s为溶液质量流量,kg·s−1;heq为与溶液表面平衡时的空气的等效比焓,kJ·kg−1;hs为溶液比焓,kJ·kg−1;
2.2 焓
为方便后文解析推导,在分析溶液与空气的热质交换时作如下假设:
1) 由于除湿/再生过程水分迁移率和溶液流率相比较小,假设溶液流量不变;
2) 忽略除湿/再生介质与环境之间散热损失,假设除湿/再生器为绝热;
3) 不考虑除湿/再生器内可能存在的局部积液及局部涡流现象,假设溶液与空气在填料表面均匀分布;
4) 不考虑溶液和空气沿与其流动垂直方向的热湿传递,假设顺逆流除湿/再生过程为一维模型;
5) 由于除湿/再生温湿度变化较窄,假设溶液和空气物性参数为常数;
6) 只考虑溶液与空气的热质交换最终处于稳态的结果,假设除湿/再生过程为稳态。
2.2.1 逆流除湿过程焓
在文献[29]中将换热器中的实际换热量与最大温差的乘积视作换热器中的最大可能温度






以逆流除湿过程为例,微元面积内的传热传质过程如图 1所示,图中qm, a, in、qm, s, in分别为进口空气和溶液的质量流量,kg·s−1;ha, in、ha, out、hs, in和hs, out分别为进、出口空气和溶液的比焓,kJ·kg−1。
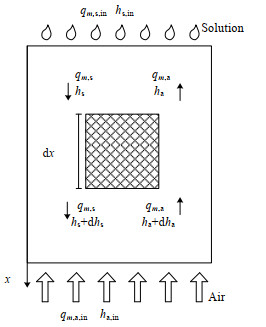
|
图 1 逆流溶液除湿过程传热传质示意图 Fig.1 Schematic diagram of heat and mass transfer of solution counter-flow dehumidification |
根据2.2节假设,可以得到逆流除湿过程的能量守恒微分方程如下:
| $ {q_{{{m, }}{\text{a}}}}{\text{d}}{h_{\text{a}}} = {q_{{{m{\text{, }}}}{\text{s}}}}{\text{d}}{h_{\text{s}}} = {\mathtt{δ}}Q $ | (6) |
积分得
| $ {q_{{{m{\text{, }}}}{\text{a}}}}({h_{{\text{a, in}}}} - {h_{{\text{a, out}}}}) = {q_{{{m{\text{, }}}}{\text{s}}}}({h_{{\text{s, out}}}} - {h_{{\text{s, in}}}}) = Q $ | (7) |
式中:Q为在微元面积上传递的全热量,kW。
根据式(4)和(5),可得微元面积内的溶液和空气的综合焓
| $ {\mathtt{δ}}{E_{h{\text{, diss}}}} = {q_{{{m, }}{\text{a}}}}{h_{\text{a}}}{\text{d}}{h_{\text{a}}} - {q_{{{m{\text{, }}}}{\text{s}}}}{h_{{\text{eq}}}}{\text{d}}{h_{\text{a}}} $ | (8) |
式中:Eh, diss为焓
将式(6)代入式(8)得
| $ {\mathtt{δ}}{E_{h{\text{, diss}}}} = {\mathtt{δ}}Q({h_{\text{a}}} - {h_{{\text{eq}}}}) $ | (9) |
在此,除湿/再生器内最大的
| $ {E_{h{\text{, diss, max}}}} = Q({h_{{\text{a, in}}}} - {h_{{\text{eq, in}}}}) $ | (10) |
为方便计算,在此定义系数j,如式(11)所示:
| $ j = \frac{{{\text{d}}{h_{{\text{eq}}}}}}{{{\text{d}}{h_{\text{s}}}}} \approx \frac{{{h_{{\text{eq}}}} - {h_{{\text{eq, in}}}}}}{{{h_{{\text{s, out}}}} - {h_{{\text{s, in}}}}}} $ | (11) |
式中:heq, in和heq, out分别为与进、出口溶液平衡的空气比焓,kJ·kg−1。
将式(11)代入式(8)并在整个除湿/再生器的面积上进行积分,得到
| $ \begin{array}{l} {E_{h{\text{, diss}}}} = \int_0^A {({q_{{{m{\text{, }}}}{\text{a}}}}{h_{\text{a}}}{\text{d}}{h_{\text{a}}} - \frac{{{q_{{{m{\text{, }}}}{\text{s}}}}{h_{{\text{eq}}}}}}{j}{\text{d}}{h_{{\text{eq}}}})} = \frac{1}{2}{q_{{{m{\text{, }}}}{\text{a}}}}(h_{{\text{a, in}}}^2 - h_{{\text{a, out}}}^2) + \frac{{{q_{{{m{\text{, }}}}{\text{s}}}}}}{{2j}}(h_{{\text{eq, in}}}^{\text{2}} - h_{{\text{eq, out}}}^2) = \hfill \\ \ \ \ \ \ \ \ \ \ \ \ {{\text{ }}_{}}{{\text{ }}_{}}\frac{1}{2}Q({h_{{\text{a, in}}}} + {h_{{\text{a, out}}}}) - \frac{1}{2}Q({h_{{\text{eq, in}}}} + {h_{{\text{eq, out}}}}) \hfill \\ \end{array} $ | (12) |
式中:A为溶液与空气的接触面积,m2。由此,可以得到逆流除湿过程中的焓
| $ E_h^{\text{*}} = \frac{{{E_{h{\text{, diss}}}}}}{{Q({h_{{\text{a, in}}}} - {h_{{\text{eq, in}}}})}} = \frac{{({h_{{\text{a, in}}}} + {h_{{\text{a, out}}}}) - ({h_{{\text{eq, in}}}} + {h_{{\text{eq, out}}}})}}{{2({h_{{\text{a, in}}}} - {h_{{\text{eq, in}}}})}} = \frac{1}{2} + \frac{1}{2}\frac{{{h_{{\text{a, out}}}} - {h_{{\text{eq, out}}}}}}{{{h_{{\text{a, in}}}} - {h_{{\text{eq, in}}}}}} $ | (13) |
逆流再生过程空气与溶液的焓



顺流除湿过程的示意图与逆流除湿过程相似,只是除湿空气和溶液流向一致,相应的焓
溶液与空气之间的能量守恒方程与总的焓
| $ - {q_{{{m{\text{, }}}}{\text{a}}}}{\text{d}}{h_{\text{a}}} = {q_{{{m{\text{, }}}}{\text{s}}}}{\text{d}}{h_{\text{a}}} = {\mathtt{δ}}Q $ | (14) |
同样微元焓
| $ {E_{h{\text{, diss}}}} = - {q_{{{m{\text{, }}}}{\text{a}}}}{h_{\text{a}}}{\text{d}}{h_{\text{a}}} - {q_{{{m{\text{, }}}}{\text{s}}}}{h_{{\text{eq}}}}{\text{d}}{h_{\text{s}}} = {\mathtt{δ}}Q({h_{\text{a}}} - {h_{{\text{eq}}}}) $ | (15) |
对方程(15)左侧进行积分得
| $ \begin{array}{l} {E_{h{\text{, diss}}}} = \int_0^A {( - {q_{{{m{\text{, }}}}{\text{a}}}}{h_{\text{a}}}{\text{d}}{h_{\text{a}}} - \frac{{{q_{m, }}_{\text{s}}{h_{{\text{eq}}}}}}{j}){\text{d}}{h_{{\text{eq}}}}} = \frac{1}{2}{q_{{{m{\text{, }}}}{\text{a}}}}(h_{{\text{a, in}}}^{\text{2}} - h_{{\text{a, out}}}^{\text{2}}) + \frac{{{q_{m, }}_{\text{s}}}}{{2j}}(h_{{\text{eq, in}}}^{\text{2}} - h_{{\text{eq, out}}}^{\text{2}}) = \hfill \\ \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, {{\text{ }}_{}}_{}\frac{1}{2}Q({h_{{\text{a, in}}}} + {h_{{\text{a, out}}}}) - \frac{1}{2}Q({h_{{\text{eq, in}}}} + {h_{{\text{eq, out}}}}) \hfill \\ \end{array} $ | (16) |
式(16)与逆流表达一样,因此可得与逆流相同的焓

由2.2节的推导可知,焓

在除湿/再生器中,其焓效率定义为
| $ 除湿:{\varepsilon _h} = \frac{{{h_{{\text{a, in}}}} - {h_{{\text{a, out}}}}}}{{{h_{{\text{a, in}}}} - {h_{{\text{eq, in}}}}}} 再生:{\varepsilon _h} = \frac{{{h_{{\text{a, out}}}} - {h_{{\text{a, in}}}}}}{{{h_{{\text{eq, in}}}} - {h_{{\text{a, in}}}}}} $ | (17) |
定义C*为与溶液平衡状态下空气与溶液之间的等效热容比,如下:
| $ C* = \frac{{{q_{{{m{\text{, }}}}{\text{a}}}} \cdot {c_{p{\text{, eq}}}}}}{{{q_{{{m{\text{, }}}}{\text{s}}}} \cdot {c_{p{\text{, s}}}}}} $ | (18) |
式中:cp, s为溶液的比定压热容,kJ·(kg·K)−1;cp, eq为与溶液平衡时的空气的比热容,kJ·(kg·K)−1。
| $ {c_{p{\text{, eq}}}} = \frac{{{\text{d}}{h_{{\text{eq}}}}}}{{{\text{d}}{T_{\text{s}}}}} \approx \frac{{{h_{{\text{eq, out}}}} - {h_{{\text{eq, in}}}}}}{{{T_{{\text{s, out}}}} - {T_{{\text{s, in}}}}}} $ | (19) |
式中:Ts为溶液的热力学温度,K;Ts, in和Ts, out分别为进、出口溶液温度,K。为了更清晰地揭示焓
| $ {h_{{\text{eq, out}}}} = C* \cdot \frac{{{q_{m, }}_{\text{s}}{c_{p{\text{, s}}}}({T_{{\text{s, out}}}} - {T_{{\text{s, in}}}})}}{{{q_{{{m{\text{, }}}}{\text{a}}}}}} + {h_{{\text{eq, in}}}} = C* \cdot \frac{{{q_{{{m{\text{, }}}}{\text{s}}}}({h_{{\text{s, out}}}} - {h_{{\text{s, in}}}})}}{{{q_{{{m{\text{, }}}}{\text{a}}}}}} + {h_{{\text{eq, in}}}} $ | (20) |
将式(20)与(17)代入式(13)可得
| $ \begin{array}{l} E_h^* = \frac{1}{2} + \frac{{{\varepsilon _h}}}{2}\frac{{{h_{{\rm{a}}, {\rm{out}}}} - {h_{{\rm{eq}}, {\rm{out}}}}}}{{{h_{{\rm{a}}, {\rm{in}}}} - {h_{{\rm{a}}, {\rm{out}}}}}} = \\ \;\;\;\;\;\;\;\frac{1}{2} + \frac{{{\varepsilon _h}}}{2}\frac{{{h_{{\rm{a}}, {\rm{out}}}} - {C^*} \cdot \frac{{{q_{m, {\rm{s}}}}\left( {{h_{{\rm{s}}, {\rm{out}}}} - {h_{{\rm{s}}, {\rm{in}}}}} \right)}}{{{q_{m, {\rm{a}}}}}} - {h_{{\rm{eq}}, {\rm{in}}}}}}{{{h_{{\rm{a}}, {\rm{in}}}} - {h_{{\rm{a}}, {\rm{out}}}}}} = \\ \;\;\;\;\;\;\;\frac{1}{2} + \frac{{{\varepsilon _h}}}{2} \cdot \frac{{{h_{{\rm{a}}, {\rm{out}}}} - {C^*}\left( {{h_{{\rm{a}}, {\rm{in}}}} - {h_{{\rm{a}}, {\rm{out}}}}} \right) - {h_{{\rm{eq}}, {\rm{in}}}} - {h_{{\rm{a}}, {\rm{in}}}} + {h_{{\rm{a}}, {\rm{in}}}}}}{{{h_{{\rm{a}}, {\rm{in}}}} - {h_{{\rm{a}}, {\rm{out}}}}}} = \\ \;\;\;\;\;\;\;\frac{1}{2} + \frac{{{\varepsilon _h}}}{2} \cdot \left( {\frac{{{h_{{\rm{a}}, {\rm{in}}}} - {h_{{\rm{eq}}, {\rm{in}}}}}}{{{h_{{\rm{a}}, {\rm{in}}}} - {h_{{\rm{a}}, {\rm{out}}}}}} - 1 - {C^*}} \right) = \\ \;\;\;\;\;\;\;1 - \frac{{1 + {C^*}}}{2} \cdot {\varepsilon _h} \end{array} $ | (21) |
从式(21)可以看出,当C*确定时,Eh*与εh为负线性关系,当C*=1时,有

为验证式(21)的线性关系的准确性,将其和公式(16)计算结果进行对比,如图 2所示。图中两公式计算结果非常一致,验证了焓


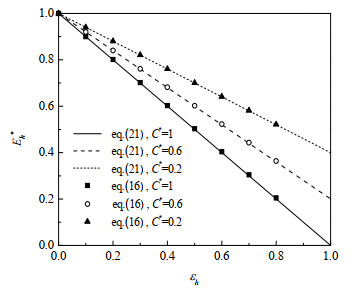
|
图 2 除湿/再生器中焓 |

溶液除湿/再生过程的不可逆损失主要取决于过程的传热单元数NTU,因此有必要对焓
| $ {\text{NTU}} = \frac{{k \cdot A}}{{{q_{{{m, }}{\text{a}}}} \cdot {c_{p{\text{, a}}}}}} $ | (22) |
式中:k为溶液与空气之间的传热系数,kW·(m2·K)−1;cp, a为空气的比定压热容,kJ·(kg·K)−1。
在除湿/再生器中,NTU与焓效率的关系如式(23)和(24)所示[15, 30],且在形式上分别与文献[29]中顺流、逆流换热器的NTU和换热效率的关系式一致:
顺流:
| $ {\varepsilon _h} = \frac{{1 - \exp \;[ - \frac{{{\text{NTU}}}}{{Le}}(1 + C*)]}}{{1 + C*}} $ | (23) |
逆流:
| $ {\varepsilon _h} = \frac{{1 - \exp \;[ - \frac{{{\text{NTU}}}}{{Le}}(1 - C*)]}}{{1 - C*\exp \;[ - \frac{{{\text{NTU}}}}{{Le}}(1 - C*)]}} $ | (24) |
式中:Le为溶液和空气间传热传质的路易斯数(近似为1[28, 30])
| $ Le = \frac{k}{{{c_{p, {\text{a}}}} \cdot {k_{\rm{m}}}}} = 1 $ | (25) |
式中:km为溶液与空气间的传质系数,kg·(m2·s)−1。将式(23)和(24)分别代入式(21)得到焓
顺流:
| $ E_h^* = \frac{1}{2} + \frac{1}{2}\exp \;[ - \frac{{{\text{NTU}}}}{{Le}}(1 + C*)] $ | (26) |
逆流:
| $ E_h^* = 1 - \frac{1}{2}\frac{{(1 + C*)\{ 1 - \exp \;[ - \frac{{{\text{NTU}}}}{{Le}}(1 - C*)]\} }}{{1 - C*\exp \;[ - \frac{{{\text{NTU}}}}{{Le}}(1 - C*)]}} $ | (27) |
从式(26)和(27)可以看出,在顺、逆流除湿/再生器中,焓

1) C*→1,
图 3为除湿/再生器中焓







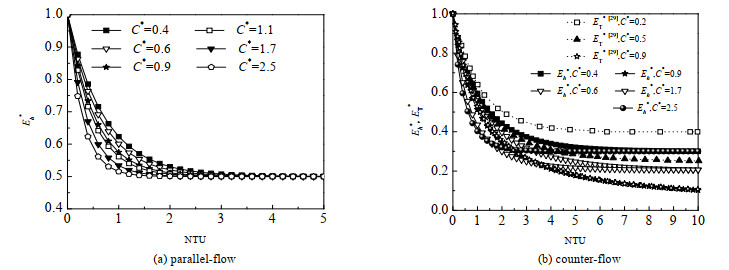
|
图 3 除湿/再生器中焓 |
从图 3(b)中显示的规律可知,仅在等效热容比C*趋于1时,逆流焓

基于焓
溶液与空气之间的能量守恒方程见式(7)。
溶液与空气之间的质量守恒方程为
| $ {q_{{{m, }}{\text{a}}}}({w_{{\text{a, out}}}} - {w_{{\text{a, in}}}}) = {q_{{{m{\text{, }}}}{\text{s}}}}({w_{{\text{s, in}}}} - {w_{{\text{s, out}}}})/{w_{{\text{s, out}}}} $ | (28) |
式中:wa, in、wa, out分别为进口、出口湿空气中水蒸气与干空气的质量比;ws, in、ws, out分别为除湿/再生器进、出口溶液中溶质与溶液质量比。
传热系数k和传质系数km可分别由空气侧的显热、含湿量和焓的增量方程决定:
| $ k = \frac{{{q_{{{m{\text{, }}}}{\text{a}}}} \cdot {c_{p{\text{, a}}}} \cdot ({T_{{\text{a, out}}}} - {T_{{\text{a, in}}}})}}{{A \cdot \Delta {T_{\text{m}}}}} $ | (29) |
式中:Ta, in和Ta, out分别为进口、出口的空气热力学温度,K;ΔTm为对数平均温差,K。
| $ {k_{\text{m}}} = \frac{{{q_{{{m{\text{, }}}}{\text{a}}}} \cdot ({w_{{\text{a, out}}}} - {w_{{\text{a, in}}}})}}{{A \cdot \Delta {w_{\text{m}}}}} $ | (30) |
| $ {k_{\text{m}}} = \frac{{{q_{{\text{m, }}}}_{\text{a}} \cdot ({h_{{\text{a, out}}}} - {h_{{\text{a, in}}}})}}{{A \cdot \Delta {h_{\text{m}}}}} $ | (31) |
式中:
在式(29)~(31)中,之所以选取3个增量方程式计算2个传热传质系数是由于
| $ \begin{array}{l} \Delta {T_{\text{m}}} = \frac{{\max \;({T_{{\text{a, in}}}} - {T_{{\text{s, out}}}}, {T_{{\text{a, out}}}} - {T_{{\text{s, in}}}}) - \min \;({T_{{\text{a, in}}}} - {T_{{\text{s, out}}}}, {T_{{\text{a, out}}}} - {T_{{\text{s, in}}}})}}{{\ln \;[{{\max \;({T_{{\text{a, in}}}} - {T_{{\text{s, out}}}}, {T_{{\text{a, out}}}} - {T_{{\text{s, in}}}})} \mathord{\left/ {\vphantom {{\max \;({T_{{\text{a, in}}}} - {T_{{\text{s, out}}}}, {T_{{\text{a, out}}}} - {T_{{\text{s, in}}}})} {\min \;({T_{{\text{a, in}}}} - {T_{{\text{s, out}}}}, {T_{{\text{a, out}}}} - {T_{{\text{s, in}}}})]}}} \right. } {\min \;({T_{{\text{a, in}}}} - {T_{{\text{s, out}}}}, {T_{{\text{a, out}}}} - {T_{{\text{s, in}}}})]}}}} \hfill \\ \Delta {w_{\text{m}}} = \frac{{\max \;({w_{{\text{a, in}}}} - {w_{{\text{eq, out}}}}, {w_{{\text{a, out}}}} - {w_{{\text{eq, in}}}}) - \min \;({w_{{\text{a, in}}}} - {w_{{\text{eq, out}}}}, {w_{{\text{a, out}}}} - {w_{{\text{eq, in}}}})}}{{\ln \;[{{\max \;({w_{{\text{a, in}}}} - {w_{{\text{eq, out}}}}, {w_{{\text{a, out}}}} - {w_{{\text{eq, in}}}})} \mathord{\left/ {\vphantom {{\max \;({w_{{\text{a, in}}}} - {w_{{\text{eq, out}}}}, {w_{{\text{a, out}}}} - {w_{{\text{eq, in}}}})} {\min \;({w_{{\text{a, in}}}} - {w_{{\text{eq, out}}}}, {w_{{\text{a, out}}}} - {w_{{\text{eq, in}}}})]}}} \right. } {\min \;({w_{{\text{a, in}}}} - {w_{{\text{eq, out}}}}, {w_{{\text{a, out}}}} - {w_{{\text{eq, in}}}})]}}}} \hfill \\ \Delta {h_m} = \frac{{\max \;({h_{{\text{a, in}}}} - {h_{{\text{eq, out}}}}, {h_{{\text{a, out}}}} - {h_{{\text{eq, in}}}}) - \min \;({h_{{\text{a, in}}}} - {h_{{\text{eq, out}}}}, {h_{{\text{a, out}}}} - {h_{{\text{eq, in}}}})}}{{\ln \;[{{\max \;({h_{{\text{a, in}}}} - {h_{{\text{eq, out}}}}, {h_{{\text{a, out}}}} - {h_{{\text{eq, in}}}})} \mathord{\left/ {\vphantom {{\max \;({h_{{\text{a, in}}}} - {h_{{\text{eq, out}}}}, {h_{{\text{a, out}}}} - {h_{{\text{eq, in}}}})} {\min \;({h_{{\text{a, in}}}} - {h_{{\text{eq, out}}}}, {h_{{\text{a, out}}}} - {h_{{\text{eq, in}}}})]}}} \right. } {\min \;({h_{{\text{a, in}}}} - {h_{{\text{eq, out}}}}, {h_{{\text{a, out}}}} - {h_{{\text{eq, in}}}})]}}}} \hfill \\ \end{array} $ | (32) |
式中:weq, in、weq, out分别表示与进口、出口溶液湿热平衡的湿空气中水蒸气与干空气质量比。
对于含湿量或温度出现交叉的情况而言,采取以下选择策略:
1) 当溶液与空气之间的温度不存在交叉时,联立方程(28)、(29)与(31)可以得到方程(33):
| $ \frac{{{T_{{\text{a, in}}}} - {T_{{\text{a, out}}}}}}{{\Delta {t_{\text{m}}}}} = Le\frac{{{h_{{\text{a, in}}}} - {h_{{\text{a, out}}}}}}{{\Delta {h_{\text{m}}}}} $ | (33) |
此时,在已知除湿/再生器焓
2) 当溶液与空气之间的温度存在交叉时,联立方程(30)和(31)得
| $ \frac{{{w_{{\text{a, in}}}} - {w_{{\text{a, out}}}}}}{{\Delta {w_{\text{m}}}}} = Le\frac{{{h_{{\text{a, in}}}} - {h_{{\text{a, out}}}}}}{{\Delta {h_{\text{m}}}}} $ | (34) |
联立方程(7)、(13)、(28)和(34)可以通过除湿/再生器工质进口状态计算得到其出口状态。
5 解析模型验证为了验证除湿/再生器解析模型的精确性,本研究将该解析模型计算结果与数值模型计算结果及实验结果分别进行了对比及分析误差。
5.1 数值模型验证在与数值模型对比时,通过文献[31]中所述的数值模型计算出一组除湿/再生器的工质出口状态参数及焓

| $ 除湿率:{q_{m, }}_{{\text{de}}} = {q_{{{m{\text{, }}}}{\text{a}}}}({w_{{\text{a, in}}}} - {w_{{\text{a, out}}}}) \text{;} \ \ \ \ 再生率:{q_{m{\text{, }}}}_{{\text{re}}} = {q_{{{m{\text{, }}}}{\text{a}}}}({w_{{\text{a, out}}}} - {w_{{\text{a, in}}}}) $ | (35) |
|
|
表 1 除湿/再生器基准工况 Table 1 Basic conditions of the dehumidifier/regenerator |
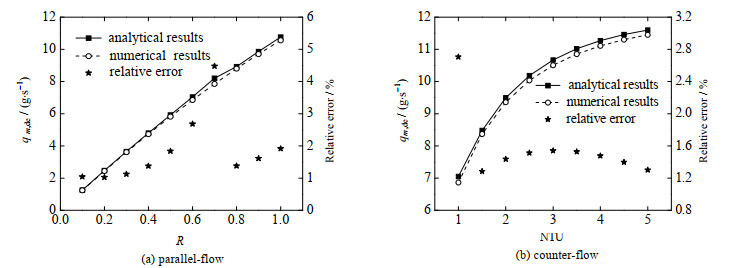
|
图 4 除湿工况下解析模型与数值模型结果对比 Fig.4 Comparison of results of the analytical model and the numerical simulation under dehumidification conditions |
|
图 5 再生工况下解析模型与数值模型结果对比 Fig.5 Comparison of results of the analytical model and the numerical simulation under regeneration conditions |
气液流量比R定义为
| $ R = \frac{{{q_{{{m{\text{, }}}}{\text{a}}}}}}{{{q_{m{\text{, }}}}_s}} $ | (36) |
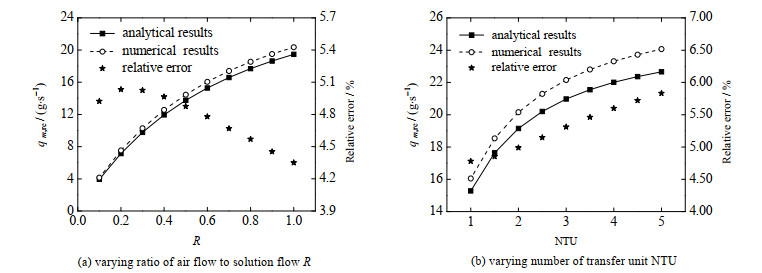
图 4和5分别显示了通过数值模型和解析模型计算得到的除湿率和再生率及两者相对误差随气液流量比R和传热单元数NTU的变化情况。从图中可以看出,当其他参数不变情况下,随R和NTU的增加,除湿/再生过程中的除湿率和再生率均逐渐升高。在模拟范围内,解析模型结果与数值模型结果的相对误差在±6%以内,平均误差为3.4%。另外,图 4(a)与4(b)中的相对误差分别在R=0.8及NTU=1.5时发生突变,前者是因为除湿工况下,随着R的增大,除湿率逐渐增加,空气释放的冷凝热也增加,溶液除湿温度随之升高。在本研究选定的基准除湿工况下,当R≤0.7时,解析模型选取对数平均温差来计算。而当R增大到0.8时,选取对数平均含湿量差来计算解析模型,模型切换过程导致了误差趋势的突变,但绝对值大小仍在允许范围内,结果的精度可接受。图 4(b)的原因与之类似。
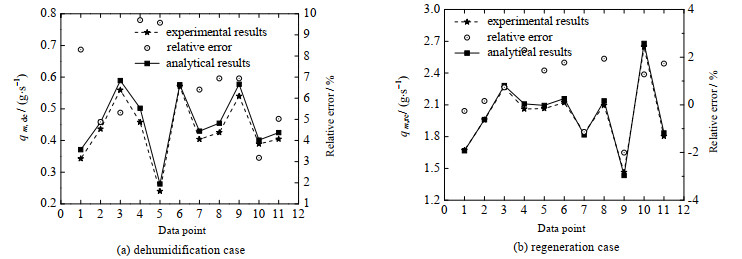
5.2 实验验证文献[32]中实验得到的除湿与再生工况数据可被用于验证逆流除湿/再生器解析模型,实验分别采用聚丙烯RauschertHiflow环和LiCl水溶液作为填料和除湿剂,填料塔为圆柱体直径为25.4 cm、高为60 cm、比表面积为210 m2·m−3,实验工况见表 2。
对比方法与4.1节类似,结果见图 6。经计算得到除湿过程的

|
图 6 解析模型与实验结果对比 Fig.6 Comparison of results of the analytical model and the experiment |
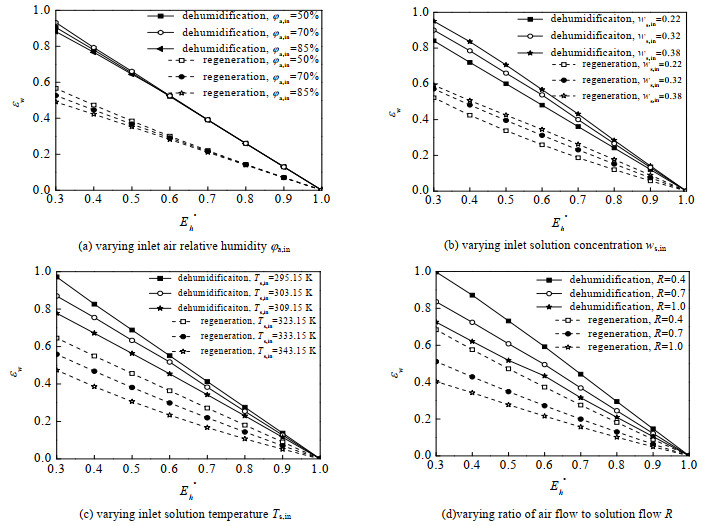
基于第4节提出的逆流除湿/再生器性能预测模型,本节分析在不同空气进口相对湿度ϕa, in、进口溶液中ws, in、温度Ts, in及R下焓

|
图 7 不同工况下除湿/再生过程焓 |
对于除湿和再生过程来说,水分的传递量是主要考虑的问题,因此采用湿效率εw来评价除湿/再生器的性能:
| $ {\varepsilon _w} = \frac{{{w_{{\text{a, in}}}} - {w_{{\text{a, out}}}}}}{{{w_{{\text{a, in}}}} - {w_{{\text{eq, in}}}}}} $ | (37) |
图 7显示随着焓

图 7(a)显示了在不同空气进口相对湿度下湿效率随焓


基于过增元定义的

(1) 类比于热量

(2) 对顺流与逆流除湿/再生器的焓

(3) 推导出基于焓
(4) 通过解析模型计算发现随着焓


| [1] |
LIU X L, QU M, LIU X B, et al. Membrane-based liquid desiccant air dehumidification: A comprehensive review on materials, components, systems and performances[J]. Renewable and Sustainable Energy Reviews, 2019, 110: 444-466. DOI:10.1016/j.rser.2019.04.018 |
| [2] |
SHUKLA D L, MODI K V. Hybrid solar still- Liquid desiccant regenerator and water distillation system[J]. Solar Energy, 2019, 182: 117-133. DOI:10.1016/j.solener.2019.02.043 |
| [3] |
苏博生, 韩巍. 低温余热/电联合驱动的双级溶液除湿系统热力性能研究[J]. 工程热物理学报, 2016, 37(11): 2296-2302. SU B S, HAN W. Performance analysis of a two-stage liquid desiccant dehumidification system driven by low temperature heat and electricity[J]. Journal of Engineering Thermophysics, 2016, 37(11): 2296-2302. |
| [4] |
CHARARA J, GHADDAR N, GHALI K, et al. Cascaded liquid desiccant system for humidity control in space conditioned by cooled membrane ceiling and displacement ventilation[J]. Energy Conversion and Management, 2019, 195: 1212-1226. DOI:10.1016/j.enconman.2019.05.102 |
| [5] |
QU X H, CAI W J, HE X X, et al. Experimental investigations on heat and mass transfer performances of a liquid desiccant cooling and dehumidification system[J]. Applied Energy, 2018, 220: 164-175. DOI:10.1016/j.apenergy.2018.03.087 |
| [6] |
WEN T, LUO Y M, WANG M, et al. Comparative study on the liquid desiccant dehumidification performance of lithium chloride and potassium formate[J]. Renewable Energy, 2021, 167: 841-852. DOI:10.1016/j.renene.2020.11.157 |
| [7] |
LIU J, LIU X H, ZHANG T. Analytical solution of heat and mass transfer process in internally cooled liquid desiccant dehumidifiers using refrigerant as cooling medium[J]. Energy Buildings, 2019, 190: 1-14. DOI:10.1016/j.enbuild.2019.02.025 |
| [8] |
WOODS J, KOZUBAL E. On the importance of the heat and mass transfer resistances in internally-cooled liquid desiccant dehumidifiers and regenerators[J]. International Journal of Heat and Mass Transfer, 2018, 122: 324-340. DOI:10.1016/j.ijheatmasstransfer.2018.01.111 |
| [9] |
LAZZARIN R M, GASPARELLA A, LONGGO A. Chemical dehumidification by liquid desiccants: theory and experiment[J]. International Journal of Refrigeration, 1999, 22(4): 334-347. DOI:10.1016/S0140-7007(98)00044-9 |
| [10] |
代彦军, 张鹤飞, 俞金娣. 错流降膜液体干燥剂除湿/再生传热传质数学模型及分析[J]. 化工学报, 2001, 52(6): 510-515. DAI Y J, ZHANG H F, YU J D. Mathematical model and analysis on heat and mass transfer of falling film liquid desiccant dehumidification in cross-flow[J]. Journal of Chemical Industry and Engineering (China), 2001, 52(6): 510-515. DOI:10.3321/j.issn:0438-1157.2001.06.009 |
| [11] |
VARELA R J, YAMAGUCHI S, GIANNETTI N, et al. General correlations for the heat and mass transfer coefficients in an air-solution contactor of a liquid desiccant system and an experimental case application[J]. International Journal of Heat and Mass Transfer, 2018, 120: 851-860. DOI:10.1016/j.ijheatmasstransfer.2017.12.089 |
| [12] |
REN C Q, JIANG Y, ZHANG Y P. Simplified analysis of coupled heat and mass transfer processes in packed bed liquid desiccant-air contact system[J]. Solar Energy, 2006, 80(1): 121-131. DOI:10.1016/j.solener.2005.01.007 |
| [13] |
BABAKHANI D, SOLEYMANI M. Simplified analysis of heat and mass transfer model in liquid desiccant regeneration process[J]. Journal of the Taiwan Institute of Chemical Engineers, 2010, 41(3): 259-267. DOI:10.1016/j.jtice.2009.10.006 |
| [14] |
SONG X, ZHANG L, ZHANG X S. NTUm-based optimization of heat or heat pump driven liquid desiccant dehumidification systems regenerated by fresh air or return air[J]. Energy, 2018, 158: 269-280. DOI:10.1016/j.energy.2018.06.037 |
| [15] |
LIU X H, JIANG Y, XIA J J, et al. Analytical solutions of coupled heat and mass transfer processes in liquid desiccant air dehumidifier/regenerator[J]. Energy Conversion and Management, 2007, 48(7): 2221-2232. DOI:10.1016/j.enconman.2006.12.009 |
| [16] |
LIANG C H, LI N F, HUANG S M. Entropy and exergy analysis of an internally-cooled membrane liquid desiccant dehumidifier[J]. Energy, 2020, 192: 116681. DOI:10.1016/j.energy.2019.116681 |
| [17] |
XIONG Z Q, DAI Y J, WANG R Z. Development of a novel two-stage liquid desiccant dehumidification system assisted by CaCl2 solution using exergy analysis method[J]. Applied Energy, 2010, 87(5): 1495-1504. DOI:10.1016/j.apenergy.2009.08.048 |
| [18] |
GUAN B, ZHANG T, JUN L, et al. Exergy analysis and performance improvement of liquid-desiccant deep-dehumidification system: An engineering case study[J]. Energy, 2020, 196: 117122. DOI:10.1016/j.energy.2020.117122 |
| [19] |
陈林, 陈群, 李震, 等. 溶液除湿性能分析和优化的湿阻法[J]. 科学通报, 2010, 55(12): 1174-1181. CHEN L, CHEN Q, LI Z, et al. Moisture resistance method for analyzing and optimizing the liquid dehumidification performance[J]. Chinese Science Bulletin, 2010, 55(12): 1174-1181. |
| [20] |
GUO Z Y, ZHU H Y, LIANG X G. Entransy—A physical quantity describing heat transfer ability[J]. International Journal of Heat and Mass Transfer, 2007, 50(13/14): 2545-2556. |
| [21] |
CHEN Q, YANG K D, WANG M, et al. A new approach to analysis and optimization of evaporative cooling system I: Theory[J]. Energy, 2010, 35(6): 2448-2454. DOI:10.1016/j.energy.2010.02.037 |
| [22] |
ZHANG L, WEI H Y, ZHANG X S. Theoretical analysis of heat and mass transfer characteristics of a counter-flow packing tower and liquid desiccant dehumidification systems based on entransy theory[J]. Energy, 2017, 141: 664-672. |
| [23] |
NAIK B K, MUTHUKUMAR P. Energy, entransy and exergy analyses of a liquid desiccant regenerator[J]. International Journal of Refrigeration, 2019, 105: 80-91. DOI:10.1016/j.ijrefrig.2018.08.016 |
| [24] |
过增元. 热学中的新物理量[J]. 工程热物理学报, 2008, 29(1): 112-114. GUO Z Y. New physical quantities in heat[J]. Journal of Engineering Thermophysics, 2008, 29(1): 112-114. DOI:10.3321/j.issn:0253-231X.2008.01.034 |
| [25] |
胡帼杰, 过增元. 传热过程的效率[J]. 工程热物理学报, 2011, 32(6): 1005-1008. HU G J, GUO Z Y. The efficiency of heat transfer process[J]. Journal of Engineering Thermophysics, 2011, 32(6): 1005-1008. |
| [26] |
陈林根.  理论及其应用的进展[J]. 科学通报, 2012, 57(30): 2815-2835. 理论及其应用的进展[J]. 科学通报, 2012, 57(30): 2815-2835.CHEN L G. Theory of entransy and the progress of its application[J]. Chinese Science Bulletin, 2012, 57(30): 2815-2835. |
| [27] |
江亿, 谢晓云, 刘晓华. 湿空气热湿转换过程的热学原理[J]. 暖通空调, 2011, 41(3): 51-64. JIANG Y, XIE X Y, LIU X H. Thermological principle of moist air heat and moisture conversion processes[J]. Heating Ventilating & Air Conditioning, 2011, 41(3): 51-64. DOI:10.3969/j.issn.1002-8501.2011.03.007 |
| [28] |
刘晓华. 溶液调湿式空气处理过程中热湿耦合传递特性分析[D]. 北京: 清华大学, 2007. LIU X H. Combined heat and mass transfer characteristic in air handling process using liquid desiccant [D]. Beijing: Tsinghua University, 2007. |
| [29] |
GOU J F, CHENG L, XU M T. Entransy dissipation number and its application to heat exchanger performance evaluation[J]. Chinese Science Bulletin, 2009, 54(15): 2708-2713. |
| [30] |
CHEN X Y, LIU X H, LI Z, et al. Analytical solution of heat and mass transfer in dehumidifier/regenerator of liquid desiccant equipment: Proceedings of the 4th International Symposium on Heating, Ventilating and Air Conditioning vol. 2 [C]. Beijing: Department of Building Science, Tsinghua University, 2003.
|
| [31] |
SONG X, ZHANG L, ZHANG X S. Analysis of the temperatures of heating and cooling sources and the air states in liquid desiccant dehumidification systems regenerated by return air[J]. Energy, 2019, 168: 651-661. DOI:10.1016/j.energy.2018.11.092 |
| [32] |
FUMO N, GOSWAMI D Y. Study of an aqueous lithium chloride desiccant system: Air dehumidification and desiccant regeneration[J]. Solar Energy, 2002, 72(4): 351-361. DOI:10.1016/S0038-092X(02)00013-0 |




