2. 浙江工业大学 化学工程学院,浙江 杭州 310014
2. College of Chemical Engineering, Zhejiang University of Technology, Hangzhou 310014, China
冷却水系统一般由冷却水塔、泵网络和终端设备三部分组成[1],是制约整个装置处理能力的关键公用工程。许多研究者从冷却水塔[2]、泵网络[3-5]以及换热网络[6-7]等子系统着手,研究侧重于能量的供应与回收[8-9],通过设计优化实现节能。也有部分研究者关注泵网络操作优化问题,给定泵网络结构后只通过变频调速、监测和先进控制等手段,调整泵运行数量和频率,实时优化系统的供应量和操作压降[10]。KOOR等[11]基于供水系统,分别研究了相同类型泵并联操作工况、同种型号的新泵和老泵并联操作工况,以及三种不同性能泵并联操作工况。MA等[12]、TIRMIZI等[13]和BENJAMIN等[14]研究了中央空调的冷却水系统,提出了变速泵的优化控制策略。上述研究针对中央冷却水系统进行操作优化,面向变负荷操作,采用先进控制策略很有必要。而化工厂冷却水系统变化频率低,泵台数少但负荷高,有安全要求不宜频繁调节。因此其操作优化更侧重于寻找一个合适的运行策略,在节能的同时更注重于长期稳定运行。
按照美国水力协会提出的寿命周期成本分析法(life cycle costs, LCC) [15],泵网络的总成本包括初始投资成本、安装调试费用、能耗费用、人工成本、维护费、停运费、环保费等,能耗、维护和其他成本远高于初始投资成本。可靠度[16]是描述泵网络长周期运行的性能指标,表示泵设备运行的高效区。如果泵长期偏离高效区运行,会严重影响寿命,增加维修维护费用。武鹏[17]将泵网络系统效率与可靠度乘积最大设为优化目标,兼顾了操作和维护费用。
本文构建考虑可靠度并联泵网络操作优化命题,针对不变频和可变频建立混合整数线性和非线性规划问题;考虑泵网络系统总功率最小和可靠度最大的目标,提出了面向工业应用的经验规则法和搜索全局最优的数学规划法,完整地描述了泵网络输出流量和能量范围,得到优化泵配置的工业和理论方案。
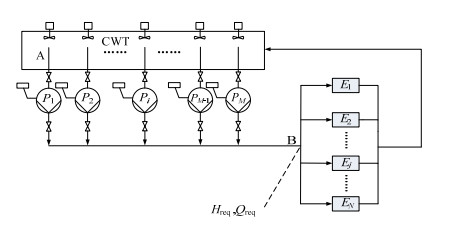
2 优化命题描述为了实现大流量与压头输出,工业装置中采用并联方式构造离心泵网络实现集中式冷却水供应。图 1所示为典型的工业冷却水系统,供水端A为并联冷却水泵网络,多个离心泵集中供水至分支点B送入用水端,以分支管路连接的多个并联终端设备Ej。用水端的需求可以通过B点总流量Qreq和总压头Hreq表示。操作优化的基本命题是调节泵系统中所有泵的开停和变频,达到用水端基本需求,消耗最少的功且保证设备运行良好。
|
图 1 工业冷却水装置并联泵网络排布简图 Fig.1 Pump network configuration of commercial cooling water systems CWT: cooling water tank; Pi: the ith pump, i∈[1, M]; Ej: the jth end user, j∈[1, N] |
泵网络操作优化目标兼顾考虑经济指标和性能指标。要在保证输送要求流量和压头前提下低能耗运行,并提高各泵运行可靠度,这是一个多目标优化问题。为了简化问题,采用总效率与可靠度乘积为目标函数,表述如下:
| $z = {\eta _{{\rm{TOT}}}}.\prod {R{s_i}} $ | (1) |
式中ηTOT代表了整个泵网络系统总效率,Rsi为第i台泵的运行可靠度。ηTOT在一定流量和压头下与总功率成反比,
| ${\eta _{{\rm{TOT}}}} = \frac{{\rho g{Q_{{\rm{TOT}}}}{H_{{\rm{TOT}}}}}}{{\sum {{y_i}{P_i}} }}$ | (2) |
式中yi∈{0, 1},表示第i台离心泵的开停状态。ΣyiPi/QTOT也称为指定压头HTOT下的单位流量冷却水消耗功率,kW·h·m-3,简称冷却水功耗,为书写方便,在下文中简写为ΣPi/Q。
研究对象是以多个单泵并联为基础的网络结构,约束条件包括流量压头并联方程[4]、变频泵性能曲线、流量扬程上下限以及物料能量衡算等:
| ${Q_{{\rm{TOT}}}} = \sum {{y_i}} {Q_i}$ | (3) |
| ${H_{{\rm{TOT}}}} = {H_i}$ | (4) |
| ${H_i} = HA \cdot {\left( {\frac{{{n_i}}}{{{n_{\rm{o}}}}}} \right)^{\rm{2}}} + HB \cdot \left( {\frac{{{n_i}}}{{{n_{\rm{o}}}}}} \right) \cdot {Q_i} + H{C_{{\rm{no}}}} \cdot {Q_i}^{\rm{2}}$ | (5) |
| ${P_i} = PA \cdot {\left( {\frac{{{n_i}}}{{{n_{\rm{o}}}}}} \right)^{\rm{3}}} + PB \cdot {\left( {\frac{{{n_i}}}{{{n_{\rm{o}}}}}} \right)^{\rm{2}}} \cdot {Q_i} + PC \cdot \left( {\frac{{{n_i}}}{{{n_{\rm{o}}}}}} \right) \cdot {Q_i}^{\rm{2}}$ | (6) |
| ${y_i} \in \left\{ {0, 1} \right\}$ | (7) |
| $Q_i^\text{L} \cdot {y_i} \leqslant {Q_i} \leqslant Q_i^\text{U} \cdot {y_i}$ | (8) |
| $H_i^\text{L} \cdot {y_i} \leqslant {H_i} \leqslant H_i^\text{U} \cdot {y_i}$ | (9) |
| $p_i^\text{L} \cdot {y_i} \leqslant {p_i} \leqslant p_i^\text{U} \cdot {y_i}$ | (10) |
| ${n_{i, \text{min}}} \cdot {y_i} \leqslant {n_i} \leqslant {n_{i, \text{max}}} \cdot {y_i}$ | (11) |
| $\text{max}(H_i^\text{L}) \leqslant {H_\text{TOT}} \leqslant \text{min}(H_i^\text{U})$ | (12) |
其中,
泵网络的操作优化命题是对固定结构的泵网络进行操作分析,通过调整泵的开停和变频最大化总效率与可靠度乘积。本文中的操作优化命题按决策变量分为开停不变频和开停且变频两种。
2.2.1 决策变量为开停不变频给定冷却水系统用水端的流量和压头需求(Hreq,Qreq),将泵只开停不变频调整的操作优化问题命名为Problem 1,此命题归属于混合整数线性规划问题(mixed integer linear programming, MILP),决策变量为二元整型变量yi∈{0, 1}可表示如下,
| ${\mathop {\max}\limits_{{y_i}} }\ z$ | (13) |
| $s.t\ \ {.^{}}^{}{Q_{{\rm{TOT}}}} = {Q_{{\rm{req}}}}$ | (14) |
| ${H_{{\rm{TOT}}}} \geqslant {H_{{\rm{req}}}}$ | (15) |
| ${n_i} = {\rm{1 450 r}} \cdot {\rm{mi}}{{\rm{n}}^{ - {\rm{1}}}}\\ 式(3)-式(12)$ | (16) |
给定冷却水系统用水端的流量和压头需求需求(Hreq, Qreq),针对开停加变频操作问题定为Problem 2,决策变量为二元整型变量yi∈{0, 1}和连续变量ni,分别表示离心泵开停状态和运行转速,因此问题归属于混合整数非线性规划问题(mixed integer nonlinear programming, MINLP)。优化命题可表示如下,
| ${\mathop {\max}\limits_{{y_i}, {n_i}} }\ z$ | (17) |
| $s.t.\ \ {Q_{{\rm{TOT}}}} = {Q_{{\rm{req}}}}$ | (14) |
| ${H_{{\rm{TOT}}}} \geqslant {H_{{\rm{req}}}}\\ 式(3)-式(12)$ | (15) |
Problem 1是MILP,本文提出经验规则法,用于工业快速应用。消去若干选项后穷举对比并将结果与所有选项穷举搜索法结果对比。Problem 2是MINLP,采用数学规划法求解。主要策略归纳如下:
(1) 经验规则法
工业现场对泵排布方案的选择并不会经过严格的数学计算,往往更多的是依赖于专业工程师的工业知识背景和现场工作经验总结,根据现场流量和压头需求,做出适当的调整,比如开停泵、调节阀门开度和关停部分终端冷却水使用设备等。本文提出经验原则为:(a)在输出压头满足的条件下,优先选择开启大泵;(b)当终端设备需水量增加时,逐一增开满足压头限制的未运行泵,增开选择遵循“先大泵后小泵”原则。
基于经验规则法,在计算平台MATLAB R2013b上编程,搜索最佳泵开停方案。
(2) 穷举搜索法
经验规则法要求快速且方便地做出判断,并不能保证结果最优。而穷举搜索法可以遍历整个流量和压头可行范围,在48个方案里筛查结果,保证搜索结果在全流量和压头可行域内全局最优。
基于穷举搜索法,在计算平台MATLAB R2013b上编程,搜索最佳泵开停方案。
(3) 数学规划法
除了开停操作,还可以为主泵添置变频设备,实现泵网络全变频操作。调整离心泵的运行频率(转速),在满足工况要求的同时可以保证泵运行在高效区,并实现节约能耗。根据WESTERLUND等[18]提出的L层泵网络超结构模型,建立主泵的3层泵网络结构模型。模型将同一型号泵归为一层,1层(Level 1)包含3台泵PA1\PA2\PA3,第2层(Level 2)包含2台泵PB1\PB2,第3层(Level 3)包含3台泵PC1\PC2\PC3。模型定义同一层运行泵的变频转速相同,且转速变化存在上下限为0.8×1450 ≤ni≤ 1450。
数学规划法以总效率和可靠度系数乘积最大为目标求解变频且开停优化方案,目标函数需改成如下形式,
| ${\mathop {\max}\limits_{{y_i}, {n_i}} }\ z = \frac{{\rho g{Q_{{\rm{TOT}}}}{H_{{\rm{TOT}}}}}}{{\sum\limits_{i = {\rm{1}}}^L {{P_i}} \cdot {N_{{\rm{P}}, i}} \cdot {y_i}}} \cdot \prod\limits_{i = {\rm{1}}}^L {Rs_i^{{N_{{\rm{p}}, i}}}} $ | (18) |
其中,L表示泵网络模型层数,此处L = 3表示3层泵网络模型;Pi表示第i层运行单泵的功率值,关联流量Qi和转速ni;Rsi表示第i层运行单泵的可靠度系数值,关联流量Qi和转速ni;Np, i表示第i层运行并联泵数量,各层并联泵数量上限值Np, 1, max = 3,Np, 2, max = 2,Np, 3, max = 3。
基于数学规划法,在计算平台GAMS 24.9上编程,求解最佳开停加变频泵网络运行方案。
3 结果与讨论以某工业冷却水系统中8台离心泵并联的网络进行操作优化。8台离心泵按型号分为3台12SH-13(位号PA1\PA2\PA3)、2台OTS200-420A (位号PB1\PB2)和3台OTS250-370A (位号PC1\PC2\PC3)。用二元整型变量yi∈{0, 1}表示位号i离心泵的开停状态。三类泵的开停方案可由三位0-1整型变量构成,共有48种开停方案,以C01-C48表示。
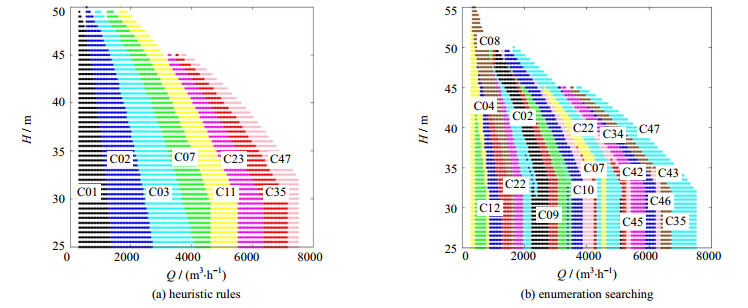
3.1 Problem 1离心泵开停方案对比将Problem 1中针对不同总流量和压头需求的开停优化方案标示在图 2中,不同颜色表示不同的开停方案,图上所标数字为方案序号。可以看出与经验规则法相比,穷举搜索法的开停方案虽然是全局最优,但用于人工操作过于复杂,总流量改变500 m3左右即需要更换开停方案。经验规则法方案调整少,更容易实现人工操作调优。
|
图 2 不同流量压头下Problem 1的泵网络操作最优方案分布 Fig.2 Optimal solution distribution of pump network operation of Problem 1 under different flow rates and heads |
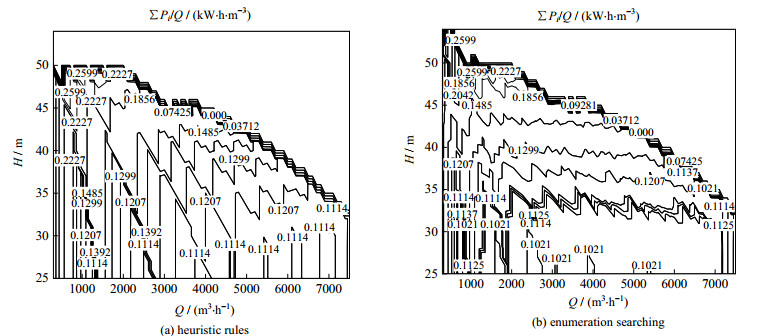
同时也对比了两种方法求解Problem 1所获得的最佳总可靠度和冷却水功耗ΣPi/Q两项子目标,将各方案的冷却水功耗画成等高线图对比于图 3。可以看出同一压头下,冷却水功耗ΣPi/Q呈现锯齿型波动,但穷举搜索法的齿型更平缓些,而采用经验规则法时,功耗随流量和压头需求变化的波动明显较大。
|
图 3 不同流量压头下Problem 1冷却水功耗等高线图 Fig.3 Optimal power consumption contour maps of Problem 1 under different flow rates and heads |
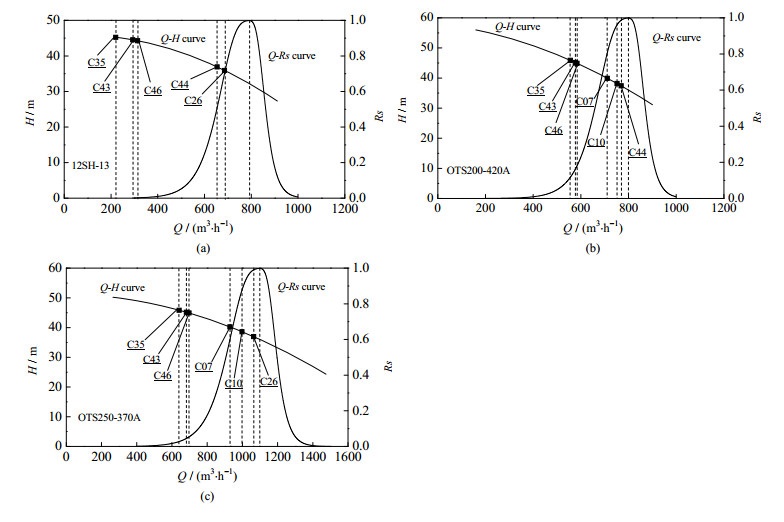
在工况Qreq = 3 500 m3·h-1,Hreq = 34 m下进行最佳总可靠度对比,采用经验规则法和穷举搜索法获得最优方案分别为C07和C10,同时为了更好的对比优化结果,引入穷举搜索法中的较优方案C26和C44和较差方案C35,C43和C46作为对比。图 4(a)~(c)分别为型号12SH-13泵、型号OTS200-420A泵和型号OTS250-370A泵流量与可靠度系数关联曲线。结果如图 4所示,Problem 1的全局最优解C10是所有方案中最优的,它不仅具有较低的冷却水功耗,方案中的单泵运行可靠度为(-,98%,84%),表明第1类泵12SH-13没有开机,第2类泵OTS200-420A运行可靠度98%,而第3类泵OTS250-370A单泵运行可靠度84%。相比之下,C07的单泵运行可靠度分别为(-,78%,58%),要比方案C10略低。相比之下次优方案C26的单泵运行可靠度为(65%,-,60%),C44为(52%,-,98%)。也就是说经验规则法得到的方案可以达到全局次优解水平。为了说明可靠度的绝对值范围,也列举了较差方案C35,C43和C46的单泵可靠度,可见各泵的可靠度都在20%以下。
|
图 4 3类单泵流量、压头和可靠度系数分布图 Fig.4 Flow rate\head\reliability comparison of single pumps |
从图 3和4可见,以系统总可靠度和系统总效率的乘积为目标进行优化时,所获得的最优方案可以兼顾泵的可靠度大和泵网络功耗小这两个目标。
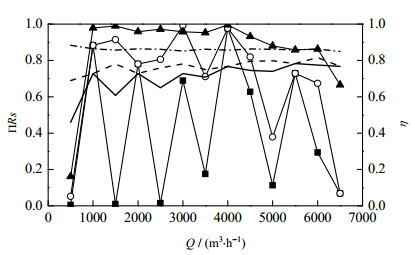
3.2 Problem 2离心泵系统优化方案以系统总效率和可靠度系数乘积最大为优化目标,采用数学规划法计算Problem 2,并与Problem 1的结果对比。在图 5中给出了扬程Hreq = 34 m时,各个输出流量下的总效率ηTOT、总泵可靠度乘积ΠRsi。图中可见,Problem 1的优化结果中,除较低负荷之外,经验规则法提供的最优解方案中冷却水功耗平均比全局最优解高11%左右,功耗和可靠度波动明显较大。而Problem 2的最优操作方案平均冷却水功耗比Problem1的全局最优解低8%左右,泵可靠度的波动也更小。
|
图 5 3个方案总效率和可靠度系数乘积相关值对比图
Fig.5 Comparison of total efficiency and reliability
—■— Problem 1 by heuristic rules-ΠRs
—○— Problem 1 by enumeration searching-ΠRs —▲— Problem 2 by mathematical programming-ΠRs —— Problem 1 by heuristic rules-η  Problem 2 by mathematical programming-η Problem 2 by mathematical programming-η
 Problem 1 by enumeration searching-η Problem 1 by enumeration searching-η
|
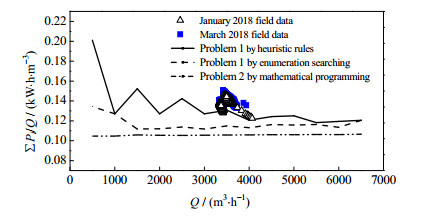
图 6则对比了同样条件下的冷却水功耗ΣPi/Q,并引入了某工厂2018年1月和3月8台离心泵运行的现场数据点3种优化策略所得到的结果中,Problem 1经验规则法获得方案的功耗最高,3 000 m3·h-1时约为0.127 kW·h·m-3,而穷举搜索Problem 1的最佳方案可以降至0.111 kW·h·m-3。当启动变频调节时,冷却水功耗还可以继续降至0.105 kW·h·m-3。各流量下数学规划法所消耗的功耗分布均一且整体位于穷举搜索法和经验规则法下方。表示相同工况下,数学规划法的最佳方案消耗总功率最小且变化平稳。
|
图 6 三个方案单位流量总功率消耗值对比图 Fig.6 Results of power consumption per cubic meter cooling water obtained by different strategies |
对并联离心泵网络集中供水的冷却水系统进行研究,本文构建了以开停和变频为手段、同时考虑泵可靠度和冷却水泵网络功耗的操作优化命题。得到如下结论:
(1) 以系统总可靠度和系统总效率的乘积为目标,对比了开停不变频和开停加变频两种操作方式的最优解,可以看出获得的最优方案可以兼顾泵的可靠度大和泵网络功耗小这两个目标。
(2) 提出了面向工业应用的经验规则算法,与穷举搜索法的全局最优解对比结果表明,采用经验规则法获得的最优解方案调整动作少,容易实现人工操作。
(3) 只开停不变频的操作优化中,除了较低负荷之外,经验规则法提供的最优解方案中冷却水功耗平均比全局最优解高11%左右,功耗和可靠度波动明显较大。
(4) 开停和变频两者均为决策变量时,最优泵系统操作方案的平均冷却水功耗比不变频时的全局最优解低8%左右,泵可靠度的波动也更小。最低冷却水功耗可以降至0.105 kW·h·m-3。
符号说明:
| D | —叶轮直径,mm | η | —效率 |
| g | —重力系数,9.81 m·s-2 | ρ | —密度,kg·m-3 |
| H | —扬程,m | 上标 | |
| HA | —扬程-流量关系式常数项系数 | L | —下限值 |
| HB | —扬程-流量关系式一次项系数 | U | —上限值 |
| HC | —扬程-流量关系式二次项系数 | 下标 | |
| NP | —每层并联泵的数量 | i | —第i台泵 |
| n | —转速,r·min-1 | M | —泵数 |
| P | —功率, kW | max | —最大值 |
| PA | —功率-流量关系式常数项系数 | min | —最小值 |
| PB | —功率-流量关系式一次项系数 | p | —并联 |
| PC | —功率-流量关系式二次项系数 | req | —需求值 |
| Q | —流量,m3·h-1 | TOT | —总量值 |
| Rs | —可靠度系数 | o | —原始不变频工况 |
| y | —整型变量 |
| [1] |
KIM J, SMITH R. Cooling water system design[J]. Chemical Engineering Science, 2001, 56(12): 3641-3658. DOI:10.1016/S0009-2509(01)00091-4 |
| [2] |
ZHENG C L, CHEN X, ZHU L Y, et al. Simultaneous design of pump network and cooling tower allocations for cooling water system synthesis[J]. Energy, 2018, 150: 653-669. DOI:10.1016/j.energy.2018.02.150 |
| [3] |
SUN J, FENG X, WANG Y F, et al. Pump network optimization for a cooling water system[J]. Energy, 2014, 67(4): 506-512. |
| [4] |
MA J Z, WANG Y F, FENG X. Simultaneous optimization of pump and cooler networks in a cooling water system[J]. Applied Thermal Engineering, 2017, 125: 377-385. DOI:10.1016/j.applthermaleng.2017.07.026 |
| [5] |
陈福利, 王彧斐, 冯霄. 带有辅泵的循环水系统研究[J]. 计算机与应用化学, 2017, 34(3): 213-216. CHEN F L, WANG Y F, FENG X. Study on an auxiliary pump network for recirculating cooling water system[J]. Computers and Applied Chemistry, 2017, 34(3): 213-216. |
| [6] |
SUN J, FENG X, WANG Y F. Cooling-water system optimization with a novel two-step sequential method[J]. Applied Thermal Engineering, 2015, 89: 1006-1013. DOI:10.1016/j.applthermaleng.2015.01.012 |
| [7] |
SUN J, FENG X, WANG Y F. Simultaneous optimization of cooler and pump networks for industrial cooling-water systems[J]. Chemical Engineering Transactions, 2015, 45: 1915-1920. |
| [8] |
MA J Z, WANG Y F, FENG X. Energy recovery in cooling water system by hydro turbines[J]. Energy, 2017, 139: 329-340. DOI:10.1016/j.energy.2017.07.166 |
| [9] |
GAO W, FENG X. The power target of a fluid machinery network in a circulating water system[J]. Chemical Engineering Transactions, 2017, 205: 847-854. |
| [10] |
祝铃钰, 施佳琪, 郑成霖, 等. 离心泵网络的节能设计与操作优化:综述与展望[J]. 高校化学工程学报, 2017, 31(6): 1245-1258. ZHU L Y, SHI J Q, ZHENG C L, et al. Energy saving design and operational optimization of centrifugal pump network:A review[J]. Journal of Chemical Engineering of Chinese Universities, 2017, 31(6): 1245-1258. DOI:10.3969/j.issn.1003-9015.2017.06.001 |
| [11] |
KOOR M, VASSILJEV A, KOPPEL T. Optimization of pump efficiencies with different pumps characteristics working in parallel mode[J]. Advances in Engineering Software, 2016, 101: 69-76. DOI:10.1016/j.advengsoft.2015.10.010 |
| [12] |
MA Z J, WANG S W. Energy efficient control of variable speed pumps in complex building[J]. Energy and Buildings, 2009, 41(2): 197-205. DOI:10.1016/j.enbuild.2008.09.002 |
| [13] |
TIRMIZI S A, GANDHIDASAN P, ZUBAIR S M. Performance analysis of a chilled water system with various pumping schemes[J]. Applied Energy, 2012, 100: 238-248. DOI:10.1016/j.apenergy.2012.05.052 |
| [14] |
BARAN B, LUCKEN C V, SOTELO A. Multi-objective pump scheduling optimization using evolutionary strategies[J]. Advanced Software Engineering, 2005, 36(1): 39-47. |
| [15] |
Hydraulic Institute, Europump, the U.S. Department of Energy's Office of Industrial Technologies. Pump life cycle costs: A guide to LCC analysis for pumping systems[M]. Parsippany: Hydraulic Institute, 2001.
|
| [16] |
BARRINGER H P. An overview of reliability engineering principles[M]. Houston: Barringer & Associates, Inc, 1996.
|
| [17] |
武鹏.并联泵组高效高可靠性运行问题研究[D].杭州: 浙江大学, 2013. WU P. Study on the parallel pump unit with high efficiency and high reliability[D]. Hangzhou: Zhejiang University, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10335-1014226151.htm |
| [18] |
WESTERLUND T, PETTERSSON F, GROSSMANN I E. Optimization of pump configurations as a MINLP problem[J]. Computers & Chemical Engineering, 1994, 18(9): 845-858. |




