1 前 言
间歇过程多用于生产小批量、高附加值产品,广泛应用于食品、精细化工以及聚合反应等领域,因其巨大的经济效益和生产灵活性,越来越受到现代过程工业的青睐。但间歇生产过程又多产生高污染的废水,近年来,国家环保条例对废水排放要求越来越高,这就要求降低间歇过程产生的废水量。因此,间歇用水过程的优化与设计在提升企业经济效益、保护环境以及节约资源等方面具有重要意义。
用水网络优化自20世纪90年代受到学术界和工业界的关注,Wang等[1] 最先提出了水夹点技术优化连续过程的用水网络,之后又有许多学者提出改进的图形法和数学规划法 [2~5]。然而上述研究多集中在连续用水过程,间歇用水过程由于涉及生产调度耦合时间维度,难度大大增加,相关研究也相对较少。
间歇过程用水网络的设计优化方法按照生产调度与用水网络的相互关系主要分为两类:分步优化法和同步优化法。当间歇过程的用水费用很小可忽略时或者出于降低模型求解复杂度考虑,通常采用分布优化先获得最优排产方案,再在所得排产方案下优化用水网络,此时,时间为参数。对于分步法预先固定生产调度下的用水网络优化问题,Wang等[6]和Foo等[7]提出了基于水夹点法的用水网络设计方法。杨霞等[8]采用时间-纯度两维用水图进行单杂质用水网络的设计。李冠华等[9]提出多周期反算策略设计单杂质用水网络。都健等[10]用数学规划法对多杂质间歇用水网络进行优化设计,并且考虑利用中间储罐跨越时间约束。叶梦晴等[11]采用矩阵编码的遗传算法优化多杂质间歇用水网络,获得较优的用水网络。
但当用水费用较高或考虑环境因素时,上述分步优化策略忽视了生产调度与用水网络之间的耦合关系,前一步所得最优调度往往限制用水网络优化空间,导致最优利润方案丢失。而同步优化法则将两个模块联立求解,时间作为全局变量,以总利润为目标函数,能更好地权衡生产费用与用水网络费用。
张珏庭等[12]采用基于状态任务网(state task network,STN)的全局事件点时间表达方式建模,同时优化间歇生产调度与单杂质用水网络,但没有考虑多杂质的情形且求解的策略为迭代法,限制了优化的空间。董宏光等[13, 14]提出状态时间空间(state time space,STS)超级结构同时设计间歇生产调度与多杂质用水网络,并且考虑了用水网络固定费用,但采用两步法迭代策略求解,且模型计算复杂度较大。 Majozi等[15, 16]基于状态顺序网 (state sequence network,SSN),采用基于设备的连续时间表达方式(与Floudas等[17]提出的特定单元事件点时间表达方式相似)建模同步优化间歇生产调度与多杂质用水网络,同时考虑水储罐和再生过程,但由于模型的时间以特定设备为基准,需要给出约束保证水进出储罐的时间一致,否则储罐中杂质浓度衡算不守恒,但这些约束却会导致部分解空间的丢失。陈诚亮等[18]提出了基于资源任务网(resource task network,RTN)的全局连续时间模型,同时还考虑了周期性调度的情形,但工艺过程与用水情形简单,问题规模较小,模型复杂度较大。Chaturvedi等 [19]考虑多个水源的间歇生产调度与用水网络同步优化,但没有考虑水的回用,不涉及非线性混合。
从以往研究可以看出时间表达方式决定了问题描述的准确性和模型的计算复杂度。而以往研究生产调度与用水网络同步优化采用的均为单一类型时间表达方式,但当用水网络考虑储罐回用和再生时,用水网络与生产调度两种时间维度相互耦合又存在差异,而这种差异恰恰导致单一时间表达方式模型存在缺陷(全局连续时间模型复杂度大和特定单元事件点模型解空间存在丢失)。为克服这一缺陷,本文采用混合时间表达方式,基于状态任务网(state task network,STN),以特定单元事件点构建生产调度模型,以非均匀离散时间点构建用水网络模型,并通过辅助约束对两部分模型进行关联,使得模型兼备了连续时间和非均匀离散时间的优势,构建了混合整数非线性规划数学模型(MINLP)。并采用分步法指导赋初值与随机扰动赋初值相结合的策略,然后调用GAMS DICOPT求解器进行求解,同步优化调度和用水网络。最后,引入两种不同间歇用水模式下的实例研究,论证混合时间模型的优势。
2 数学模型
2.1 问题描述
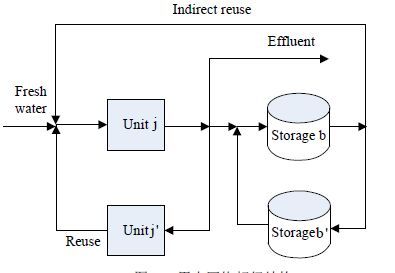
生产多种产品的间歇化工厂,已知其工艺流程、设备操作能力、原料初始量、生产过程涉及用水操作,已知其杂质负荷,采用“混合器-用水单元-分配器”用水网络超级结构(图 1),设备用水来源包括:新鲜水、其它设备产生的废水、来自储罐的废水;设备产生的废水流向包括:用以其它设备直接回用,去水储罐用以间接回用,废水处理。优化目标为获得最优生产调度和用水网络从而在整个生产周期内达到利润最大。
以下是问题的一些基本假设:
(1) 进出水只发生在生产过程开始和结束或结束之后(清洗),且只在过程端点进行物料衡算。
(2) 任务切换时间相较于加工时间很小,可忽略。
(3) 用水过程中的杂质浓度增加或损失以杂质负荷形式给出,忽略用水过程中水量的增加和损耗。
2.2 生产调度模型
建立生产调度模型时,基于状态任务网(state task network,STN)表示工艺生产流程,采用特定单元事件点时间表达方式划分时间域,以下为生产调度模型关键约束:
1) 物料衡算:表示物质s在事件点n时的库存量等于上一事件点n-1的库存量加上生产量再减去当前事件点n的销售量与生产消耗量。
|
$s{t_{s,n}} = s{t_{s,n - 1}} - {D_{s,n}} + \sum\limits_{i \in {{\rm{I}}_{\rm{j}}}} {{\rm{\rho }}_{s,i}^{\rm{P}}\sum\limits_{j \in {{\rm{J}}_{\rm{i}}}} {B{a_{i,j,n - 1}}} } - \sum\limits_{i \in {{\rm{I}}_{\rm{j}}}} {{\rm{\rho }}_{s,i}^{\rm{C}}\sum\limits_{j \in {{\rm{J}}_{\rm{i}}}} {B{a_{i,j,n}}} } \;\;\;\forall s \in {\rm{S}},n \in {\rm{N}}$
|
(1) |
2) 分配约束:表示在事件点n设备j只能进行一个生产任务,wvi,j,n为二元变量。
|
$\sum\limits_{i \in {{\rm{I}}_{\rm{j}}}} {w{v_{i,j,n}} \le 1} \;\;\;\;\;\;\forall j \in {\rm{J}},n \in {\rm{N}}$
|
(2) |
3) 生产能力约束:表示生产设备的加工能力限制。
|
${\rm{V}}_{i,j}^{{\rm{min}}}w{v_{i,j,n}} \le B{a_{i,j,n}} \le {\rm{V}}_{i,j}^{{\rm{max}}}w{v_{i,j,n}}\;\;\;\;\;\;\;\;\;\;\;\;\;\forall i \in {\rm{I}},j \in {{\rm{J}}_{\rm{i}}},n \in {\rm{N}}$
|
(3) |
4) 库存约束:表示物质s在事件点n的库存量不超过最大库存量stmaxs。
|
$s{t_{s,n}} \le {\rm{stma}}{{\rm{x}}_s}\;\;\;\;\;\;\forall s \in {\rm{S}},n \in {\rm{N}}$
|
(4) |
5) 时间范围约束:表示生产任务的起始和结束时间都在调度周期内。
|
$T{f_{i,j,n}} \le H\;\;\;\;\;\;\forall i \in {\rm{I}},j \in {{\rm{J}}_{\rm{i}}},n \in {\rm{N}}$
|
(5) |
|
$T{s_{i,j,n}} \le H\;\;\;\;\;\;\forall i \in {\rm{I}},j \in {{\rm{J}}_{\rm{i}}},n \in {\rm{N}}$
|
(6) |
6) 过程持续时间约束:生产任务结束时间等于开始时间加上过程持续时间。
|
$T{f_{i,j,n}} = T{s_{i,j,n}} + {a_{i,j}}w{v_{i,j,n}} + b{m_{i,j}}B{a_{i,j,n}}\;\;\;\;\;\;\;\;\;\;\forall i \in {\rm{I}},j \in {{\rm{J}}_{\rm{i}}},n \in {\rm{N}}$
|
(7) |
7) 时间顺序约束:式(8)-(10)表示同一设备相同生产任务的时间顺序,式(11)表示同一设备不同生产任务的时间顺序,式(12)表示不同设备不同生产任务的时间顺序。式(13)表示同一设备生产任务的时间紧约束。
|
$T{s_{i,j,n + 1}} \ge T{f_{i,j,n}} - H(1 - w{v_{i,j,n}})\;\;\;\forall i \in {\rm{I}},j \in {{\rm{J}}_{\rm{i}}},n \in {\rm{N}}$
|
(8) |
|
$T{s_{i,j,n + 1}} \ge T{s_{i,j,n}}\;\;\;\;\;\;\forall i \in {\rm{I}},j \in {{\rm{J}}_{\rm{i}}},n \in {\rm{N}}$
|
(9) |
|
$T{f_{i,j,n + 1}} \ge T{f_{i,j,n}}\;\;\;\;\;\;\forall i \in {\rm{I}},j \in {{\rm{J}}_{\rm{i}}},n \in {\rm{N}}$
|
(10) |
|
$T{s_{i,j,n + 1}} \ge T{f_{i',j,n}} - H(1 - w{v_{i',j,n}})\;\;\;\;\forall i \in {{\rm{I}}_{\rm{j}}},i' \in {{\rm{I}}_{\rm{j}}},i \ne i',j \in {\rm{J}},n \in {\rm{N}}$
|
(11) |
|
$T{s_{i,j,n + 1}} \ge T{f_{i',j',n}} - H(1 - w{v_{i',j',n}})\;\;\;\forall i \in {{\rm{I}}_{\rm{j}}},i' \in {{\rm{I}}_{\rm{j}}},i \ne i',j,j' \in {\rm{J}},n \in {\rm{N}}$
|
(12) |
|
$T{s_{i,j,n + 1}} \ge \sum\limits_{n' \in {\rm{N}}}^{n' \le n} {\sum\limits_{i' \in {{\rm{I}}_{\rm{j}}}} {(T{f_{i',j,n'}} - T{s_{i',j,n'}})} } \;\;\;\forall i \in {\rm{I}},j \in {{\rm{J}}_{\rm{i}}},n \in {\rm{N}}$
|
(13) |
2.3 生产调度与用水网络关联约束
生产调度模型中采用特定单元事件点划分时域会导致相同事件点的实际时间不一致,通过关联约束将时间非均匀离散,从而避免用水网络中时间点处的物料不守恒。
1) 用水过程与生产调度的时间顺序约束:当用水过程与生产任务时间一致时采用式(14)~(15),当用水过程为生产任务结束后的清洗采用式(16)~(21)代替式(8)、(11)和(13),iw是涉及用水的生产任务,Dwiw,j为清洗时间,Tiw,j,nin和Tiw,j,nout为用水过程进出水的时间。
|
$T_{{i_w},j,n}^{{\rm{in}}} = T{s_{{i_w},j,n}}\;\;\;\forall {i_w} \in {{\rm{I}}_w},\;j \in {{\rm{J}}_{{i_w}}},n \in {\rm{N}}$
|
(14) |
|
$T_{{i_w},j,n}^{{\rm{out}}} = T{f_{{i_w},j,n}}\;\;\;\forall {i_w} \in {{\rm{I}}_w},\;\;j \in {{\rm{J}}_{{i_w}}},n \in {\rm{N}}$
|
(15) |
|
$T_{{i_w},j,n}^{{\rm{in}}} = T{f_{{i_w},j,n}}\;\;\;\forall {i_w} \in {{\rm{I}}_w}\;,\;j \in {{\rm{J}}_{{i_w}}},n \in {\rm{N}}$
|
(16) |
|
$T_{{i_w},j,n}^{{\rm{out}}} = T_{{i_w},j,n}^{{\rm{in}}} + D{w_{{i_w},j}}w{v_{{i_w},j,n}}\;\;\;\;\;\forall {i_w} \in {{\rm{I}}_w},j \in {{\rm{J}}_{{i_w}}},n \in {\rm{N}}$
|
(17) |
|
$T{s_{{i_w},j,n + 1}} \ge T_{{i_w},j,n}^{{\rm{out}}} - H(1 - w{v_{{i_w},j,n}})\;\;\;\forall {i_w} \in {\rm{I}},j \in {{\rm{J}}_{{{\rm{i}}_{\rm{w}}}}},n \in {\rm{N}}$
|
(18) |
|
$T{s_{{i_w},j,n + 1}} \ge T_{{i_w}',j,n}^{{\rm{out}}} - H(1 - w{v_{{i_w}',j,n}})\;\;\;\;\forall {i_w} \in {{\rm{I}}_{\rm{j}}},{i_w}' \in {{\rm{I}}_{\rm{j}}},{i_w} \ne {i_w}',j \in {{\rm{J}}_{{{\rm{i}}_{\rm{w}}}}},n \in {\rm{N}}$
|
(19) |
|
$T{s_{{i_w},j,n + 1}} \ge \sum\limits_{n' \in {\rm{N}}}^{n' \le n} {\sum\limits_{{i_w}' \in {{\rm{I}}_{\rm{j}}}} {(T_{_{{i_w}',j,n'}}^{{\rm{out}}} - T{s_{{i_w}',j,n'}})} } \;\;\;\forall {i_w} \in {{\rm{I}}_{\rm{j}}},j \in {{\rm{J}}_{{{\rm{i}}_{\rm{w}}}}},n \in {\rm{N}}$
|
(20) |
|
$T_{{i_w},j,n}^{{\rm{out}}} \le H\;\;\;\;\forall {i_w} \in {{\rm{I}}_{\rm{w}}},j \in {{\rm{J}}_{{{\rm{i}}_{\rm{w}}}}},n \in {\rm{N}}$
|
(21) |
2) 时间非均匀离散约束:将特定单元事件点表示的实际时间进行非均匀离散,式(22)~(25)将水网中的非均匀离散时间Tt与调度中时间Tiw,j,nin和Tiw,j,nout进行交互关联。
|
$T_{{i_w},j,n}^{{\rm{in}}} \le {T_t} + H(1 - w_{_{{i_w},j,n,t}}^{{\rm{in}}})\;\;\;\;\;\;\;\forall {i_w} \in {{\rm{I}}_w},\;j \in {{\rm{J}}_{{i_w}}},\;n \in {\rm{N}},\;t \in {\rm{T}}$
|
(22) |
|
$T_{{i_w},j,n}^{{\rm{in}}} \ge {T_t} - H(1 - w_{_{{i_w},j,n,t}}^{{\rm{in}}})\;\;\;\;\forall {i_w} \in {{\rm{I}}_w},\;j \in {{\rm{J}}_{{i_w}}},\;n \in {\rm{N}},\;t \in {\rm{T}}$
|
(23) |
|
$T_{{i_w},j,n}^{{\rm{out}}} \le {T_t} + H(1 - w_{_{{i_w},j,n,t}}^{{\rm{out}}})\;\;\;\;\;\forall {i_w} \in {{\rm{I}}_w},\;j \in {{\rm{J}}_{{i_w}}},\;n \in {\rm{N}},\;t \in {\rm{T}}$
|
(24) |
|
$T_{{i_w},j,n}^{{\rm{out}}} \ge {T_t} - H(1 - w_{_{{i_w},j,n,t}}^{{\rm{out}}})\;\;\;\;\;\;\;\forall {i_w} \in {{\rm{I}}_w},\;j \in {{\rm{J}}_{{i_w}}},\;n \in {\rm{N}},t \in {\rm{T}}$
|
(25) |
|
${T_{t + 1}} > {T_t}\;\;\forall t \in {\rm{T}}$
|
(26) |
|
${T_t} \le H\;\;\;\forall t \in {\rm{T}}$
|
(27) |
3) 分配关联约束:式(28)、(29)表示是否进出水等价于是否有用水的生产任务进行,式(30)、(31) 表示用水任务进水或出水的时刻点t均对应一个事件点n。
|
$w{v_{{i_w},j,n}} = \sum\limits_t {w_{_{{i_w},j,n,t}}^{{\rm{in}}}} \;\;\;\;\;\;\forall {i_w} \in {{\rm{I}}_w},\;j \in {{\rm{J}}_{{i_w}}},n \in {\rm{N}},\;t \in {\rm{T}}$
|
(28) |
|
$w{v_{{i_w},\;j,n}} = \sum\limits_t {w_{_{{i_w},j,n,t}}^{{\rm{out}}}} \;\;\;\;\;\forall {i_w} \in {{\rm{I}}_w},\;j \in {{\rm{J}}_{{i_w}}},\;n \in {\rm{N}},t \in {\rm{T}}$
|
(29) |
|
$\sum\limits_n {w_{_{{i_w},j,n,t}}^{{\rm{in}}}} \; \le 1\;\;\;\;\;\;\forall {i_w} \in {{\rm{I}}_w},\;j \in {{\rm{J}}_{{i_w}}},n \in {\rm{N}},\;t \in {\rm{T}}$
|
(30) |
|
$\sum\limits_n^{} {} w_{{i_w},j,n,t\;}^{{\rm{out}}} \le 1\;\;\;\;\forall {i_w} \in {{\rm{I}}_w}\;,j \in {{\rm{J}}_{{i_w}}},\;n \in {\rm{N}}\;,t \in {\rm{T}}$
|
(31) |
2.4 用水网络模型
用水网络基于图 1的超级结构建模,考虑水的直接回用和水储罐间接回用,模型采用非均匀离散时间表达方式,以准确表示进出水的实际时间,保证物料守恒。
1) 水物料衡算:式(32)表示生产消耗的水来自于储罐mb,iw,j,t,其他任务的废水mriw',j',iw,j,t以及新鲜水mf,iw,j,t,式(33)表示产生的废水流向储罐miw,j,b,t,其他任务回用mriw,j,iw',j',t以及废水处理厂miw,j,e,t。式(36)为进水流股的杂质衡算式,物料衡算式(34)、(35)和(37)、(38)只在有用水过程时约束才激活有效,式中的M取大于右侧的一个常数,以保证约束成立,是一个常数,表示用水过程持续的时间点数。其中,$m{r_{{i_w}',j',{i_w},j,t}}$表示在t时间点设备j’中的任务iw’产生
的废水直接回用于设备j中的用水任务iw的水量。
|
$\;m_{{i_w},j,t}^{{\rm{in}}} = \sum\limits_{b \in {\rm{B}}} {{m_{b,{i_w},j,t}}} + \sum\limits_{{i_w}' \in {{\rm{I}}_{\rm{w}}}} {\sum\limits_{j' \in {{\rm{J}}_{{{\rm{i}}_{\rm{w}}}}}} {m{r_{{i_w}',j',{i_w},j,t}}} } + \sum\limits_{f \in {\rm{F}}} {{m_{f,{i_w},j,t}}} \;\;\forall {i_w} \in {{\rm{I}}_{\rm{w}}}\;,j \in {{\rm{J}}_{{{\rm{i}}_{\rm{w}}}}},t \in {\rm{T}}$
|
(32) |
|
$m_{{i_w},j,t}^{{\rm{out}}} = \sum\limits_{b \in {\rm{B}}} {{m_{{i_w},j,b,t}}} + \sum\limits_{{i_w}' \in {{\rm{I}}_{\rm{w}}}} {\sum\limits_{j' \in {{\rm{J}}_{{{\rm{i}}_{\rm{w}}}}}} {m{r_{{i_w},j,{i_w}',j',t}}} } + \sum\limits_{e \in {\rm{E}}} {{m_{{i_w},j,e,t}}} \;\;\;\;\forall {i_w} \in {{\rm{I}}_w}\;,j \in {{\rm{J}}_{{i_w}}},t \in {\rm{T}}$
|
(33) |
|
$\begin{align}
& m_{{{i}_{w}},j,t}^{\text{in}}\ge m_{{{i}_{w}},j,{{t}_{p}}}^{\text{out}}-M_{{{i}_{w}},j}^{\text{max}}(2-\sum\limits_{n\in \text{N}}{w_{_{{{i}_{w}},j,n,t}}^{\text{in}}}-\sum\limits_{n\in \text{N}}{w_{_{{{i}_{w}},j,n,{{t}_{p}}}}^{\text{out}})} \\
& \forall {{i}_{w}}\in {{\text{I}}_{w}}\ ,j\in {{\text{J}}_{{{i}_{w}}}},t,{{t}_{p}}\in \text{T},t<{{t}_{p}}\le t+\text{ }\!\!\Delta\!\!\text{ t} \\
\end{align}$
|
(34) |
|
$\begin{align}
& \ m_{{{i}_{w}},j,t}^{\text{in}}\le m_{{{i}_{w}},j,{{t}_{p}}}^{\text{out}}+M_{{{i}_{w}},j}^{\text{max}}(2-\sum\limits_{n\in \text{N}}{w_{_{{{i}_{w}},j,n,t}}^{\text{in}}}-\sum\limits_{n\in \text{N}}{w_{_{{{i}_{w}},j,n,{{t}_{p}}}}^{\text{out}})}\ \ \ \ \ \ \ \ \ \\
& \forall {{i}_{w}}\in {{\text{I}}_{w}}\ ,\ j\in {{\text{J}}_{{{i}_{w}}}},t,{{t}_{p}}\in \text{T},t<{{t}_{p}}\le t+\text{ }\!\!\Delta\!\!\text{ t} \\
\end{align}$
|
(35) |
|
$\begin{align}
& m_{{{i}_{w}},j,t}^{\text{in}}c_{{{i}_{w}},j,c,t}^{\text{in}}=\sum\limits_{b\in \text{B}}{{{m}_{b,{{i}_{w}},j,t}}}c_{b,c,t}^{\text{b,out}}+\sum\limits_{{{i}_{w}}'\in {{\text{I}}_{\text{w}}}}{\sum\limits_{j'\in {{\text{J}}_{{{\text{i}}_{\text{w}}}}}}{m{{r}_{{{i}_{w}}',j',{{i}_{w}},j,t}}}}c_{{{i}_{w}}',j',c,t}^{\text{out}} \\
& \forall {{i}_{w}}\in {{\text{I}}_{w}}\ ,j\in {{\text{J}}_{{{i}_{w}}}},c\in \text{C},t\in \text{T} \\
\end{align}$
|
(36) |
|
$\begin{array}{l}
m{l_{{i_{w,j,c}}}} + m_{{i_w},j,t}^{{\rm{in}}}c_{{i_w},j,c,t}^{{\rm{in}}} \ge m_{{i_w},j,{t_p}}^{{\rm{out}}}c_{{i_w},j,c,{t_p}}^{{\rm{out}}} - M(2 - \sum\limits_{n \in {\rm{N}}} {w_{_{{i_w},j,n,t}}^{{\rm{in}}}} - \sum\limits_{n \in {\rm{N}}} {w_{_{{i_w},j,n,{t_p}}}^{{\rm{out}}})} \;\;\\
\begin{array}{*{20}{c}}
{\begin{array}{*{20}{c}}
{\begin{array}{*{20}{c}}
{}&{}
\end{array}}&{}&{}
\end{array}}&{}&{}&{}
\end{array}\forall {i_w} \in {{\rm{I}}_{\rm{w}}}\;,\;j \in {{\rm{J}}_{{{\rm{i}}_{\rm{w}}}}},c \in {\rm{C}},t,{t_p} \in {\rm{T}}\;,t < {t_p} \le t + {\rm{\Delta t}}
\end{array}$
|
(37) |
|
$\begin{align}
& m{{l}_{{{i}_{w,j,c}}}}+m_{{{i}_{w}},j,t}^{\text{in}}c_{{{i}_{w}},j,c,t}^{\text{in}}\le m_{{{i}_{w}},j,{{t}_{p}}}^{\text{out}}c_{{{i}_{w}},j,c,{{t}_{p}}}^{\text{out}} \\
& +M(2-\sum\limits_{n\in \text{N}}{w_{_{{{i}_{w}},j,n,t}}^{\text{in}}}-\sum\limits_{n\in \text{N}}{w_{_{{{i}_{w}},j,n,{{t}_{p}}}}^{\text{out}})}\ \ \\
& \forall {{i}_{w}}\in {{\text{I}}_{w}},\ j\in {{\text{J}}_{{{i}_{w}}}},c\in \text{C},t,{{t}_{p}}\in \text{T},t<{{t}_{p}}\le t+\text{ }\!\!\Delta\!\!\text{ t} \\
\end{align}$
|
(38) |
2) 杂质浓度约束:进出水的杂质浓度不超过进出口最大浓度$C_{{i_w},j,c}^{{\rm{in,max}}}\;$和$C_{{i_w},j,c}^{{\rm{out,max}}}$。
|
$c_{{i_w},j,c,t}^{{\rm{in}}} \le C_{{i_w},j,c}^{{\rm{in,max}}}\;\;\;\;\;\forall {i_w} \in {{\rm{I}}_w}\;,j \in {{\rm{J}}_{{i_w}}},c \in {\rm{C}},t \in {\rm{T}}$
|
(39) |
|
$c_{{i_w},j,c,t}^{{\rm{out}}} \le {\rm{C}}_{{i_w},j,c}^{{\rm{out,max}}}\;\;\;\;\forall {i_w} \in {{\rm{I}}_w},j \in {{\rm{J}}_{{i_w}}},c \in {\rm{C}},t \in {\rm{T}}$
|
(40) |
3) 进出水量约束:式(41)、(42)为进出混合流股的水量限制,式(43)~(45)分别为由储罐,其他任务和新鲜水源向用水任务iw供水的水量限制,式(46)~(48)分别为任务iw产生的废水流向储罐,其他任务和废水处理设施的水量限制,且二元变量求和式$\sum\limits_{n \in {\rm{N}}} {w_{_{{i_w},\;j,n,\;t}}^{{\rm{in}}}} $和$\sum\limits_{n \in {\rm{N}}} {w_{_{{i_w},j,n,t}}^{{\rm{out}}}} $为0时,生产任务无进出水,限制进出水量为0。
|
$M_{{i_w},j}^{{\rm{min}}}\sum\limits_{n \in {\rm{N}}} {w_{_{{i_w},j,n,t}}^{{\rm{in}}}} \le m_{{i_w},j,t}^{{\rm{in}}} \le M_{{i_w},j}^{\max }\sum\limits_{n \in {\rm{N}}} {w_{_{{i_w},j,n,t}}^{{\rm{in}}}} \;\;\;\;\forall {i_w} \in {{\rm{I}}_w}\;,j \in {{\rm{J}}_{{i_w}}},t \in {\rm{T}}$
|
(41) |
|
$M_{{i_w},j}^{{\rm{min}}}\sum\limits_{n \in {\rm{N}}} {w_{_{{i_w},j,n,t}}^{{\rm{out}}}} \le m_{{i_w},j,t}^{{\rm{out}}} \le M_{{i_w},j}^{\max }\sum\limits_{n \in {\rm{N}}} {w_{_{{i_w},j,n,t}}^{{\rm{out}}}} \;\;\;\;\;\;\;\forall {i_w} \in {I_w}\;,j \in {J_{{i_w}}},t \in {\rm{T}}$
|
(42) |
|
${m_{b,{i_w},j,t}} \le M_{{i_w},j}^{{\rm{max}}}\sum\limits_{n \in {\rm{N}}} {w_{_{{i_w},\;j,n,\;t}}^{{\rm{in}}}} \;\;\;\;\;\;\;\forall b \in B,{i_w} \in {I_w},j \in {J_{{i_w}}},t \in T$
|
(43) |
|
$m{r_{{i_w}',j',{i_w},j,t}} \le M_{{i_w},j}^{{\rm{max}}}\sum\limits_{n \in {\rm{N}}} {w_{_{{i_w},j,n,t}}^{{\rm{in}}}} \;\;\;\;\;\;\;\;\;\;\forall {i_w},{i_w}' \in {I_w},j,j' \in {J_{{i_w}}},\;t \in {\rm{T}}$
|
(44) |
|
${m_{f,{i_w},j,t}} \le M_{{i_w},j}^{{\rm{max}}}\sum\limits_{n \in {\rm{N}}} {w_{_{{i_w},j,n,t}}^{{\rm{in}}}} \;\;\;\;\;\forall f \in {\rm{F}},{i_w} \in {I_w},j \in {J_{{i_w}}},t \in {\rm{T}}$
|
(45) |
|
${m_{{i_w},j,b,t}} \le M_{{i_w},j}^{{\rm{max}}}\sum\limits_{n \in {\rm{N}}} {w_{_{{i_w},j,n,t}}^{{\rm{out}}}} \;\;\;\;\;\;\forall {i_w} \in {I_w},j \in {J_{{i_w}}},b \in B,t \in T$
|
(46) |
|
$m{r_{{i_w},j,{i_w}',j',t}} \le M_{{i_w},j}^{{\rm{max}}}\sum\limits_{n \in {\rm{N}}} {w_{_{{i_w},j,n,t}}^{{\rm{out}}}} \;\;\;\;\;\;\;\;\;\forall {i_w},{i_w}' \in {I_w},j,j' \in {J_{{i_w}}},\;t \in T$
|
(47) |
|
${m_{{i_w},j,e,t}} \le M_{{i_w},j}^{{\rm{max}}}\sum\limits_{n \in {\rm{N}}} {w_{_{{i_w},j,n,t}}^{{\rm{out}}}} \;\;\;\;\;\;\;\forall {i_w} \in {I_w},j \in {J_{{i_w}}},e \in E,t \in T$
|
(48) |
4) 水储罐约束:式(49)为储罐进水流股杂质衡算,式(50)表示储罐的水来自于用水过程产生的废水以及其它储罐,式(51)表示储罐中的水可供生产使用和其它储罐使用。式(52)、(53)表示t时刻储罐的水量和杂质等于前一时刻的量加上当前时刻流入的再减去当前时刻流出的,式(54)给出储罐的最大储水量,式(55)限制调度周期完成时储罐中的储水量为0,T0为调度周期结束时的时间点。
|
$m_{b,t}^{{\rm{b,in}}}c_{b,c,t}^{{\rm{b,in}}} = \sum\limits_{{i_w} \in {{\rm{I}}_{\rm{w}}}} {\sum\limits_{j \in {{\rm{J}}_{{{\rm{i}}_{\rm{w}}}}}} {{m_{{i_w},j,b,t}}c_{{i_w},j,c,t}^{{\rm{out}}}} } + \sum\limits_{b' \in {\rm{B}},b' \ne b} {m{b_{b',b,t}}c_{b',c,t}^{{\rm{b,out}}}} \;\forall b \in B,c \in C,t \in T$
|
(49) |
|
$m_{b,t}^{{\rm{b,in}}}c_{b,c,t}^{{\rm{b,in}}} = \sum\limits_{{i_w} \in {{\rm{I}}_{\rm{w}}}} {\sum\limits_{j \in {{\rm{J}}_{{{\rm{i}}_{\rm{w}}}}}} {{m_{{i_w},j,b,t}}c_{{i_w},j,c,t}^{{\rm{out}}}} } + \sum\limits_{b' \in {\rm{B}},b' \ne b} {m{b_{b',b,t}}c_{b',c,t}^{{\rm{b,out}}}} \;\forall b \in B,c \in C,t \in T$
|
(50) |
|
$m_{b,t}^{{\rm{b,out}}} = \sum\limits_{{i_w} \in {{\rm{I}}_{\rm{w}}}} {\sum\limits_{j \in {{\rm{J}}_{{{\rm{i}}_{\rm{w}}}}}} {{m_{b,{i_w},j,t}}} } + \sum\limits_{b' \in {\rm{B}},b' \ne b} {m{b_{b,b',t}}} \;\;\;\;\;\;\forall b \in B,t \in T$
|
(51) |
|
${v_{b,t}}c_{b,c,t}^{{\rm{b,out}}} = {v_{b,t - 1}}c_{b,c,t - 1}^{{\rm{b,out}}} + m_{b,t}^{{\rm{b,in}}}c_{b,c,t}^{{\rm{b,in}}} - m_{b,t}^{{\rm{b,out}}}c_{b,c,t}^{{\rm{b,out}}}\;\;\;\;\;\;\;\;\forall b \in B,c \in C,t \in T$
|
(52) |
|
${v_{b,t}} = {v_{b,t - 1}} + m_{b,t}^{{\rm{b,in}}} - m_{b,t}^{{\rm{b,out}}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\forall b \in B,t \in T$
|
(53) |
|
${v_{b,t}} \le {\rm{v}}_{\rm{b}}^{{\rm{max}}}\;\;\;\;\;\;\forall b \in B,t \in T$
|
(54) |
|
${v_{b,{{\rm{T}}_{\rm{0}}}}} = 0\;\;\;\;\;\;\;\;\;\forall b \in B$
|
(55) |
2.5 目标函数
以一个操作周期内总利润为目标函数,总利润为产品利润减去新鲜水费用,再减去废水处理费用,式(56)$\sum\limits_{sr \in {\rm{Sr}}} {{\rm{p}}{{\rm{f}}_{sr}}({\rm{STI}}{{\rm{N}}_{sr}} - s{t_{sr,{\rm{N}}}}} )$中为原料费用,$\sum\limits_{sp \in {\rm{Sp}}} {{{\rm{p}}_{sp}}s{t_{sp,{\rm{N}}}}} $为产品销售额,$\sum\limits_{t \in {\rm{T}}} {\sum\limits_{f \in {\rm{F}}} {\sum\limits_{{i_w} \in {{\rm{I}}_{\rm{w}}}} {\sum\limits_{j \in {{\rm{J}}_{{{\rm{i}}_{\rm{w}}}}}} {{m_{f,{i_w},j,t}}{\rm{cf}}} } } } $为新鲜水的费用,$\sum\limits_{t \in {\rm{T}}} {\sum\limits_{e \in {\rm{E}}} {\sum\limits_{{i_w} \in {{\rm{I}}_{\rm{w}}}} {\sum\limits_{j \in {{\rm{J}}_{{{\rm{i}}_{\rm{w}}}}}} {{m_{{i_w},j,e,t}}} {\rm{ce}}} } } $为废水处理费用。
|
$\begin{align}
& \max :PROFIT=\sum\limits_{sp\in \text{Sp}}{{{\text{p}}_{sp}}s{{t}_{sp,N}}}-\sum\limits_{sr\in \text{Sr}}{\text{p}{{\text{f}}_{sr}}(\text{STI}{{\text{N}}_{sr}}-s{{t}_{sr,N}}}) \\
& \ -\sum\limits_{t\in \text{T}}{\sum\limits_{f\in \text{F}}{\sum\limits_{{{i}_{w}}\in {{\text{I}}_{\text{w}}}}{\sum\limits_{j\in {{\text{J}}_{{{\text{i}}_{\text{w}}}}}}{{{m}_{f,{{i}_{w}},j,t}}\text{cf}}}}}-\sum\limits_{t\in \text{T}}{\sum\limits_{e\in \text{E}}{\sum\limits_{{{i}_{w}}\in {{\text{I}}_{\text{w}}}}{\sum\limits_{j\in {{\text{J}}_{{{\text{i}}_{\text{w}}}}}}{{{m}_{{{i}_{w}},j,e,t}}}\text{ce}}}} \\
\end{align}$
|
(56) |
3 求解策略
采用特定单元事件点和非均匀离散时间混合时间表达方式,构建了混合整数非线性模型(MINLP)。但是二元变量与非线性的耦合会导致模型的计算复杂度剧增,为克服求解难度,保证优化效率,采用分步法指导赋初值与随机扰动赋初值相结合的策略进行模型求解,具体步骤如下:
(1) 采用分步法用以指导赋初值(MILP-NLP),第一步设计出最优生产调度(MILP问题),然后给定生产调度设计初始用水网络(NLP问题),从分步法中筛选关键变量的解作为MINLP模型的部分初值。
(2) 确定性算法与随机扰动策略相结合,选择DICOPT求解器作为MINLP模型的求解器,其中CONOPT 作为NLP的求解器,CPLEX为MILP的求解器。由(1)得到的关键变量初值指导随机扰动赋初值并多次迭代求解,对比结果,筛选出较好的局部最优解。
4 算例研究
4.1 算例一
算例一取自文献[18],某间歇化工厂,三种原料(原料1,2,3)分别经三个平行操作的间歇装置(U1,U2,U3)生产出三种产品(产品1,2,3),操作周期为8 h,过程持续时间分别为2,2.5,1.5 h,操作相关参数见表 1。由表 1可见,装置1只产生杂质c1,装置2只产生杂质c2,然而,装置3却产生三种质(c1,c2,c3)。对于生产过程1,2,3,每消耗原料1 kg,则消耗水量为0.333,0.5,0.667 kg,算例一不考虑废水的处理费用,所以目标函数(式56)无最后一项,表 2为费用参数。
表 1(Tab. 1)

表 1 算例一用水过程参数
Table 1 Parameters for water using process-example 1
| Process | Contaminant | Ciw,cin,max/ppm | Ciw,cout,max/ppm | Mliw,c/g | Limiting flow/ton |
| 1 | c1 | 5 | 15 | 675 | 67.5 |
| c2 | 0 | 0 | 0 | |
| c3 | 0 | 0 | 0 | |
| 2 | c1 | 0 | 0 | 0 | 50.0 |
| c2 | 50 | 100 | 2500 | |
| c3 | 0 | 0 | 0 | |
| 3 | c1 | 120 | 220 | 5600 | 56.0 |
| c2 | 200 | 450 | 14000 | |
| c3 | 200 | 9500 | 520800 | |
|
表 1 算例一用水过程参数
Table 1 Parameters for water using process-example 1 |
表 2(Tab. 2)

表 2 算例一的费用参数
Table 2 Costs in example 1
| Process | Price/$·ton-1 | Cost of raw material/ $·ton-1 | Cost of fresh water/$·ton-1 |
| 1 | 2300 | 108 | 1000 |
| 2 | 2000 | 82 | 1000 |
| 3 | 1050 | 95 | 1000 |
|
表 2 算例一的费用参数
Table 2 Costs in example 1 |
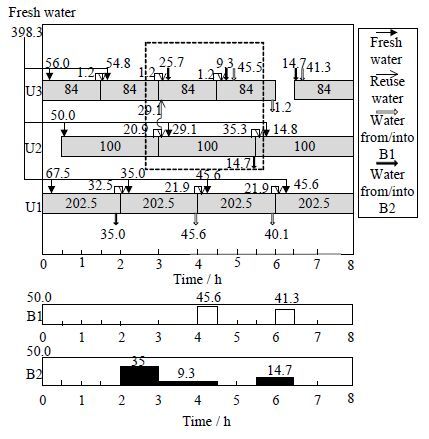
优化结果如图 2所示,图中给出调度甘特图、具体用水过程以及储罐水量随时间的变化(B1,B2为储罐),优化后的用水网络包括多处直接回用和间接回用,耗水量大幅降低,结果显示新鲜水用量398.3 ton,目标利润值为2353770 $\$$,而分步优化的新鲜水用量为544 ton,目标利润值为2208019 $\$$,所以采用同步优化利润同比增长了6.60%,耗水量降低了26.78%。与文献[15]和[18]的相比(表 3),该模型优化利润最高,分别提升了2.77%和0.08%;与文献[18] 的模型相比,模型约束和二元变量较多,连续变量较少,非线性约束数相同;与文献[15]的模型相比,混合时间模型避免了解空间的丢失,因为文献[15]为避免水物料衡算出现偏差,给出回用时间顺序约束(式(30)~(46)[15]),而这些约束却会损失部分水回用结构(例:图 2虚线框中水回用结构)。
表 3(Tab. 3)

表 3 算例一结果对比
Table 3 Comparison with related results in references-example 1
| Modeling approach |
RTN based[18] |
SSN based[15] |
STN based (this paper)
|
| Time representation |
Continuous time |
Unit-specific event point |
Unit-specific event point/discrete
|
| Problem structure |
MINLP |
MINLP |
MINLP
|
| Nno. of time points/intervals |
11 |
8 |
6/11
|
| No. of cont. variables |
1470 |
832 |
1275
|
| No. of bin. variables |
81 |
192 |
414
|
| No. of constraints |
2768 |
3512 |
3125
|
| No. of nonlinear constraints |
474 |
207 |
474
|
| Solution space loss |
no |
loss |
no
|
| Profit / $ |
2351775 |
2290370 |
2353770
|
|
表 3 算例一结果对比
Table 3 Comparison with related results in references-example 1 |
4.2 算例二
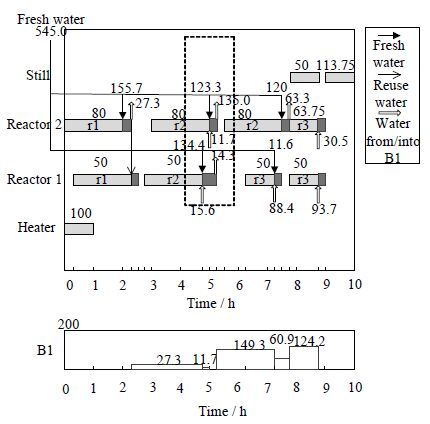
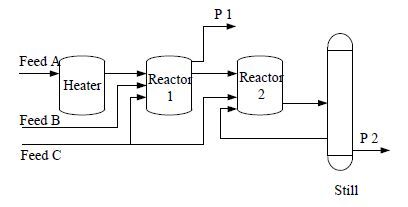
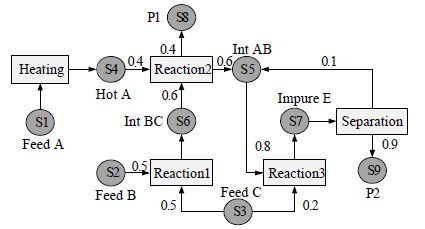
算例二取自文献[16],算例二的工艺网络更复杂,其间歇操作的特性更突出,用水过程为反应器的清洗过程,保证一批反应任务结束后,反应器能不含污垢继续进行下一批反应,与算例一相比,问题复杂度大幅增加,求解难度增加。工艺流程图如图 4所示,包括一台加热器,两台反应器(R1,R2),一座精馏塔,反应器可以进行多个反应,生产网络灵活,可以生产多种产品,状态任务示意图(STN)如图 5所示,用水过程相关数据如表 4、表 5所示,产品售价为100 $·kg-1,新鲜水费用为2 $·kg-1,废水处理费用为3 $·kg-1 (其生产过程相关数据见文献[16],不考虑废水再生过程)。图 3给出了优化后的调度与具体用水过程以及储罐水量随时间的变化(B1为储罐),优化后的用水网络包括水的直接回用与间接回用,降低了耗水量与废水排放量。同步优化后的新鲜水消耗量为 545.0 kg,目标利润为20450 $\$$,而分步优化新鲜水消耗量为747.5 kg,目标利润为19438 $\$$,所以采用同步优化利润同比增长了5.21%,耗水量降低了27.09%。与文献[16]和[18]的相比(表 6),优化利润最高,分别提升了1.34%和1.71%;与文献[18]的模型相比,模型时间点数、约束和连续变量较少,二元变量较多,非线性约束大幅减少,计算复杂度大幅削减;与文献[16]的模型相比,混合时间模型避免了解空间的丢失,因为文献[16]为避免水物料衡算出现偏差,给出回用时间顺序约束(式(33)~(47)[16]),而这些约束却会损失部分水回用结构(例:图 3虚线框中水回用结构)。
表 4(Tab. 4)

表 4 算例二杂质负荷与清洗时间
Table 4 Mass load and washing duration in example 2
| Reaction tasks | Mass load (c1/g) | Mass load (c2/g) | Mass load (c3/g) | Duration of washing / h |
| Reaction 1(R1) | 4 | 80 | 10 | 0.25 |
| Reaction 1(R2) | 15 | 24 | 358 | 0.3 |
| Reaction 2(R1) | 28.5 | 7.5 | 135 | 0.5 |
| Reaction 2(R2) | 9 | 2 | 16 | 0.25 |
| Reaction 3(R1) | 15 | 80 | 85 | 0.25 |
| Reaction 3(R2) | 22.5 | 45 | 36.5 | 0.25 |
|
表 4 算例二杂质负荷与清洗时间
Table 4 Mass load and washing duration in example 2 |
表 5(Tab. 5)

表 5 算例二杂质进出口最大浓度
Table 5 Maximum inlet/outlet contaminant concentrations in example
| Reaction tasks | | c1 / g·kg-1 | c2 / g·kg-1 | c3/ g·kg-1 |
| Reaction 1 (R1) | Max. inlet | 0.5 | 0.5 | 2.3 |
| Max. outlet | 1 | 0.9 | 3 |
| Reaction 2 (R1) | Max. inlet | 0.01 | 0.05 | 0.3 |
| Max. outlet | 0.2 | 0.1 | 1.2 |
| Reaction 3 (R1) | Max. inlet | 0.15 | 0.2 | 0.35 |
| Max. outlet | 0.3 | 1 | 1.2 |
| Reaction 1 (R2) | Max. inlet | 0.05 | 0.2 | 0.05 |
| Max. outlet | 0.1 | 1 | 12 |
| Reaction 2 (R2) | Max. inlet | 0.03 | 0.1 | 0.2 |
| Max. outlet | 0.075 | 0.2 | 1 |
| Reaction 3 (R2) | Max. inlet | 0.3 | 0.6 | 1.5 |
| Max. outlet | 2 | 1.5 | 2.5 |
|
表 5 算例二杂质进出口最大浓度
Table 5 Maximum inlet/outlet contaminant concentrations in example |
表 6(Tab. 6)

表 6 算例二结果对比
Table 6 Comparison with related results in references - example 2
| Modeling approach
|
RTN based[18]
|
SSN based[16]
|
STN based (this paper)
|
| Time representation
|
Continuous time
|
Unit-specific event point
|
Unit-specific event point /discrete
|
| Problem structure
|
MINLP
|
MINLP
|
MINLP
|
| No. of time points/intervals
|
16
|
10
|
7/10
|
| No. of cont. variables
|
5049
|
1913
|
2451
|
| No. of bin. Variables
|
630
|
278
|
896
|
| No. of constraints
|
7315
|
6887
|
5404
|
| No. of nonlinear constraints
|
1746
|
399
|
747
|
| Solution space loss
|
no
|
loss
|
no
|
| Profit/$
|
20106
|
20180
|
20450
|
|
表 6 算例二结果对比
Table 6 Comparison with related results in references - example 2 |
5 结 论
模型采用了混合时间表达方式,生产调度模型采用特定单元事件点时间表达方式,用水网络模型采用非均匀离散时间表达方式,然后用关联约束将两种时间维度进行有效关联,建立了调度与用水网络同步优化的数学模型,并且引入实例进行模型验证,证明同步优化与分步优化相比,大幅降低了用水量,实现了经济、环保和资源的综合优化。最后,对比前人单一时间表达方式模型,发现基于混合时间表达方式的数学模型具有以下两个优势:
(1) 用水网络模型采用非均匀离散时间表达方式,弥补了特定单元事件点表达方式的缺陷,无需增加时间顺序约束以保证用水过程物料守恒,从而避免因约束太强导致解空间缺失。
(2) 与全局连续时间表达方式和均匀离散时间表达方式相比,混合时间模型时间点数较少,尤其当间歇生产工艺及用水过程愈加复杂时,这一优势更加明显,而时间点的减少会导致模型约束数以及非线性约束数大幅减少,从而降低模型求解复杂度。
符号说明:
表 (Tab. )

表
Table
| a,bm |
- 生产调度任务处理时间参数 |
Tin,Tout |
- 生产用水任务进出水时间,h
|
| Ba |
- 生产调度模型物料的处理量 |
v |
- 储罐中的储水量
|
| cin,cout |
- 用水任务进出水的杂质浓度 |
Vmin,Vmax |
- 设备的最小与最大生产量
|
| cb,in,cb,out |
- 储罐进出水的杂质浓度 |
Vbmax |
- 储罐最大储水量
|
| Cin,max,Cout,max |
- 进出水的杂质最大浓度 |
win,wout |
- 二元变量:生产任务是否进/出水
|
| cf,ce |
- 新鲜水费用与废水处理费用 |
wv |
- 二元变量:生产任务是否执行
|
| D |
- 生产调度模型的物质销售量 |
ρp ρc |
- 设备的进料与出料分配系数
|
| Dw |
- 清洗时间,h |
下标与集合 |
|
| H |
- 生产调度的时间长度,h |
b,b’∈ B |
- 水储罐及集合
|
| Min,Mmax |
- 用水任务的最小和最大用水量 |
c∈ C |
- 杂质组分及集合
|
| m |
- 用水任务分支流股水量(不包括直接回用流股) |
e∈ E |
- 废水及集合
|
| mb,in,mb,out |
- 储罐进出水量 |
f∈ F |
- 新鲜水及集合
|
| min,mout |
- 用水任务进出水量 |
i,i’∈ I |
- 操作任务及集合
|
| mb |
- 储罐之间转移的水量 |
i∈ Ij |
- j设备执行的任务及集合
|
| ml |
- 用水过程的杂质负荷,g |
iw,iw’∈Iw |
- 涉及用水的生产任务及集合
|
| mr |
- 直接回用流股水量 |
j,j’∈ J |
- 设备单元及集合
|
|
P,Pf |
- 产品与原料价格 |
j∈ Ji |
- 执行任务i的设备单元及集合
|
|
PROFIT |
- 一个操作周期的总利润 |
j∈ |
- 执行任务iw的设备单元及集合
|
|
STIN,stmax |
- 最初库存量与最大库存量 |
n∈ N |
- 单元事件点及集合
|
|
st |
- 生产调度模型物料的库存量 |
s∈ S |
- 物料状态及集合
|
|
Tt |
- 非均匀离散时间变量,h |
sr∈ Sr,sp∈Sp |
- 原料,产品状态及集合
|
|
Ts,Tf |
- 事件点处任务开始和结束间,h |
t,tp ∈T |
— 离散时间点及集合
|
|
表
Table |