2. 齐鲁工业大学(山东省科学院)海洋仪器仪表研究所, 山东 青岛 266100
2. Institute of Oceanographic Instrumentation, Qilu University of Technology (Shandong Academy of Sciences), Qingdao 266100, China
流体振荡器是一种能在出口产生连续振荡射流的流体器件,具有无运动部件、结构简单、运行稳定、操作方便、安全可靠等优点,可以应用于航空航天[1-2]、强化传热[3]、石油化工[4-5]、生物能源[6-7]、煤矿浮选[8]、膜除污[9-10]等领域。
在流体振荡器中,流体流入喷嘴后形成主射流,由于射流扩散和卷吸作用,这股射流会发生偏转并被低压吸引到邻近壁面上附壁流动,形成科恩达效应[11]。主射流在振荡腔内来回切换,周而复始形成周期性振荡。完成一次周期性振荡的时间为振荡周期,而主射流在单位时间内的振荡次数即为振荡频率f。反馈回路的存在则有助于流体振荡器在没有任何运动部件的情况下自动实现振荡。Hao等[12]对流体振荡器进行了三维大涡模拟和可视化实验,结果表明分布在振荡腔和主射流之间的涡流以及左右两侧压差会驱动主射流偏转。别海燕等[13]建立了正反馈式流体振荡器的三维数值模型,分析了振荡器内部流动特性。Ming等[14]采用非定常雷诺平均N-S湍流模型研究了自激流体振荡器阵列的流体动力学和传热性能。Pandey等[15]采用三维非定常雷诺平均N-S方程对流体振荡器进行数值研究,结果表明射流流动结构和振荡频率与已有实验结果有较好一致性,入口宽度显著影响流体振荡器性能。Zheng等[16]采用雷诺应力湍流模型对横向气流和静止气流中的流体振荡器进行数值研究,阐明了流体振荡器的射流振荡机制。Tesař等[17]利用流体振荡器搅拌气流,再将气流注入曝气器中产生微气泡,这类微气泡可用于传热传质和废水处理。李辉等[18]介绍了流体振荡器耦合微孔膜产生气泡的应用进展。
气液两相流是现今流体力学的研究热点,含有微气泡的流体流动在环境治理、工业应用、生物医药等[19-22]众多领域中起着重要作用。国内外学者已经对流体振荡器的理论和数值模拟进行了广泛研究,而对流体振荡器在气液两相流中的研究较少。因此本研究采用数值模拟方法对流体振荡器中的气液两相流进行研究,借助ANSYS Fluent模拟气泡在流场中的碎化行为,探究振荡频率、液速和气泡初始直径对流体中气泡运动和破碎的影响,揭示流体振荡器气泡碎化特性,阐明流体振荡器可作为一种新型气泡发生装置,并为后续流体振荡器的实验研究和性能提升提供理论基础。同时,本研究也进行了可视化实验,以此来验证数值模拟结果的准确性和可靠性。
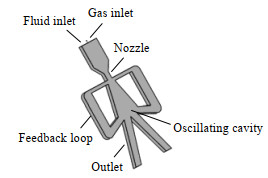
2 实验 2.1 流体振荡器结构流体振荡器结构如图 1所示,主要包括气相入口、液相入口、喷嘴、反馈回路、振荡腔和出口支路。液相入口长度、宽度分别为14、8 mm,喷嘴宽度为4 mm,振荡腔长度为34 mm,两侧反馈回路长度为60 mm,两个出口支路长为38 mm,宽为5 mm,并形成一个34°夹角。为了保证流体充分发展,采用3D打印技术制作一个长度为300 mm的射流管道。流体振荡器则用聚甲基丙烯酸甲酯(polymethyl methacrylate, PMMA)制作而成。
|
图 1 流体振荡器结构示意图 Fig.1 Schematic diagram of the fluidic oscillator |
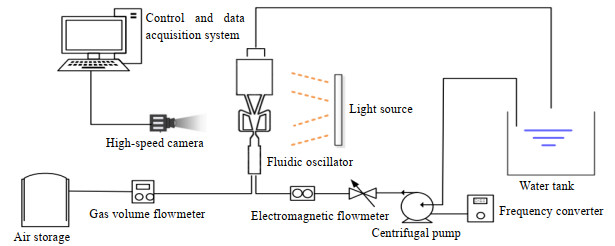
实验在室温下进行,以水和空气为工作介质,具体流程如图 2所示。水由离心泵输送到流体振荡器中,使用电磁流量计调节水速,液相质量流量为0.1 ~ 0.5 kg⋅s−1。空气由注射器注入气相入口,使用气体流量计调节气速,气相体积流量为0.01~0.05 L⋅min−1。高速摄像系统主要由计算机、高速相机(Photron FASTCAM Mini WX)和LED光源组成,通过高速拍摄可以获得清晰完整的气泡运动过程。
|
图 2 实验装置示意图 Fig.2 Schematic diagram of the experimental setup |
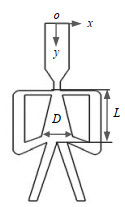
流体振荡器的几何结构对内部流动结构和性能有重要影响,通过改变流体振荡器振荡腔的长径比(L/D),可以得到不同尺寸参数的流体振荡器。如图 3所示,L为振荡腔长度,D为反馈管之间的距离。保持振荡腔长度L = 34 mm,设计4种不同尺寸的流体振荡器,长径比分别为1.1、1.3、1.5和1.85。
|
图 3 流体振荡器振荡腔结构 Fig.3 Oscillating cavity structure of the fluidic oscillator |
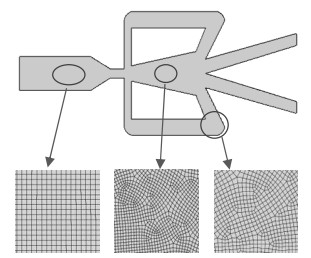
网格质量和网格数量会影响模拟结果的准确性,所以在模拟之前需要进行网格无关性检验,以此来确保计算精度和结果准确性。如图 4所示,本研究采用六面体网格对流体振荡器进行网格划分,并对主射流区域进行局部加密,在提高网格质量的同时保证了瞬态模拟的精度和准确性。
|
图 4 流体振荡器网格划分示意图 Fig.4 Grid mesh of the fluidic oscillator |
此外,分别构建网格数量为54 977、80 975、114 125、130 617和150 634的5组流体振荡器模型进行网格无关性检验,通过模拟直径为5 mm的气泡在流体振荡器中的运动变化,比较网格数量对振荡频率和气泡界面的影响。在模拟时监控出口流量随时间的变化情况,得到周期性变化的出口流量时均值,再通过快速傅里叶变换获得出口流量的脉动频域,脉动频域中出现的最大峰值为流体振荡器的振荡频率。
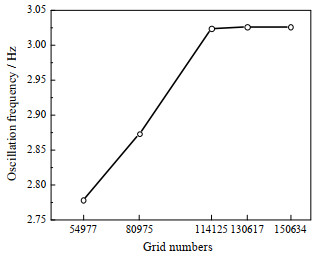
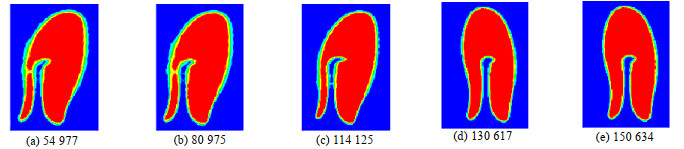
如图 5所示,随着网格数量增加,流体振荡器振荡频率逐渐趋于稳定。当网格数量大于114 125时,网格数对振荡频率几乎无影响。图 6显示了气泡初始直径为5 mm时不同网格数量对气泡界面的影响。相较于其他网格数,网格数量为130 617时气泡界面最清晰。当网格数量为150 634时,气泡界面稍微变薄但不明显。因此,综合考虑计算精度和成本,最终选取网格数量为130 617的模型进行后续模拟计算。
|
图 5 网格无关性检验 Fig.5 Grid independence verification |
|
图 6 不同网格数量气泡界面 Fig.6 Bubble interfaces with different grid numbers |
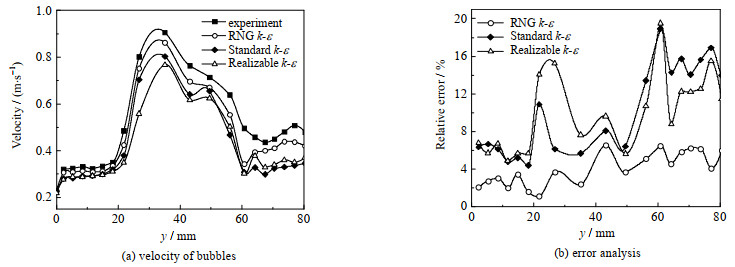
由于流体振荡器内部流场复杂,流动具有强烈的各向异性,因此需要选择适当的湍流模型对其进行数值模拟。目前常用的湍流模型有Standard k-ε模型、Realizable k-ε模型和RNG k-ε模型。而RNG k-ε模型引入了时均应变率,加入了旋流的影响,对计算精度有较大改善。为了验证湍流模型的准确性和可靠性,搭建实验装置,对比不同湍流模型的气泡上升速度数值模拟结果和实验结果。其中,入口液速均为0.25 m⋅s−1,气泡初始直径为4 mm。如图 7 (a)所示,图中y为从入口到出口的距离,相比于Standard k-ε模型和Realizable k-ε模型,RNG k-ε模型得到的气泡上升速度结果与实验结果具有较好的一致性。图 7 (b)显示了3种模型的模拟值与实验值的相对误差,从图中可以发现RNG k-ε模型相对误差最小。因此,选用RNG k-ε湍流模型对流体振荡器进行模拟计算。
|
图 7 湍流模型验证与相对误差分析 Fig.7 Turbulence model validation and relative error analysis |
采用Fluent 15.0的RNG k-ε湍流模型对流体振荡器进行非稳态模拟,待流场稳定后采用VOF两相流模型对气-液相界面进行追踪。选用水和空气为流体介质,入口采用速度入口边界,出口采用压力出口。湍流指定方法采用湍流强度和水力直径,其中湍流强度I由式(1)计算得出。压力-速度耦合采用压力耦合方程组的半隐式方法,体积分数函数采用几何重构法,压力差值采用PRESTO,压力离散采用二阶迎风格式,瞬态方程采用一阶隐式。计算时间步长设为1.0×10−5 s,每步迭代20次,以保证较高稳定性和收敛精度。
| $ I = 0.16{{R}}{{{e}}^{ - 1/8}} $ | (1) |
式中:Re为雷诺数。
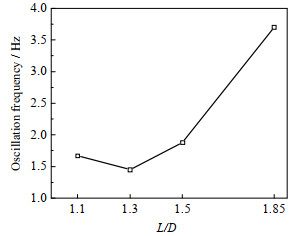
4 结果与讨论 4.1 振荡频率对气泡破碎的影响振荡频率f是衡量流体振荡器的重要性能参数,而流体振荡器的结构形状对振荡频率有很大影响。设计4种流体振荡器,长径比(L/D)分别为1.1、1.3、1.5和1.85。如图 8所示为不同振荡腔长径比对振荡频率的影响,随着长径比增大,振荡频率呈先下降后上升的趋势。
|
图 8 振荡腔长径比对振荡频率的影响 Fig.8 Effects of length to diameter ratio of oscillating cavity on oscillation frequency |
为了研究振荡频率对气泡碎化效果的影响,对不同结构的流体振荡器进行气泡破碎数值模拟。图 9(a)中,长径比为1.1时,f = 1.67 Hz,此时初始气泡由喷嘴进入振荡腔,从气泡主体直接脱离出一个较小子气泡,随后初始气泡主体受射流偏转的影响靠近壁面移动,并再次发生较为明显的碎化。在图 9(b)、9 (c)和9 (d)中,长径比为1.3、1.5和1.85时,对应的振荡频率分别为1.45、1.88和3.7 Hz。位于振荡腔入口的初始气泡发生变形,均形成“颈部”结构,并在流场作用下发生破碎。破碎后形成的子气泡处于主射流区域,在偏转射流影响下沿着振荡腔边壁运动。由于主射流速度梯度较大,边壁处的子气泡表面产生黏性剪切应力,当剪切应力大于子气泡表面张力时,子气泡发生二次破碎。随着振荡频率增大,子气泡二次破碎后形成的小气泡数量增多,流体振荡器气泡碎化效果也随之增强。因此,选用振荡频率为3.7 Hz,即长径比为1.85的流体振荡器进行后续模拟。

|
图 9 不同振荡频率时气泡破碎情况 Fig.9 Bubble breakup at varying oscillation frequencies |
液速是影响气泡破碎的重要因素,Uesewa等[23]研究发现液速越大,气泡碎化程度越高。在振荡器入口位置,注入初始直径为4 mm的气泡,设置不同的入口液速,相对应的喷嘴液速v分别为1.05、2.14、3.20、4.29、5.41 m⋅s−1。发现不同喷嘴液速下气泡具有不同的破碎形式和破碎机制。如图 10所示,当v= 1.05 m⋅s−1时,因为液速较低,气泡发生变形但并未破碎。当v分别为2.14和3.20 m⋅s−1时,气泡从喷嘴进入振荡腔后拉伸变形并发生凹陷,湍流旋涡与气泡间相互作用加强,气泡界面不稳定性增强,最后破碎形成子气泡。随着喷嘴液速增加到4.29和5.41 m⋅s−1,气泡进入喷嘴后迅速变形并破碎成子气泡,其碎化程度明显。这是因为液速增大导致湍流强度和速度梯度增大,湍流脉动和旋涡碰撞使气泡更容易发生破碎。

|
图 10 不同喷嘴液速时气泡变形及破碎图 Fig.10 Deformation and breakup of bubbles at different liquid velocities in the nozzle |
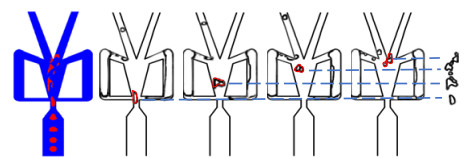
图 11对比了v= 2.14 m⋅s−1时流体振荡器中模拟和实验的气泡破碎结果。其中左边第一个黑色的图为模拟图,其余4个为实验图,从图中可以看出,气泡进入流体振荡器后在偏转射流的作用下向左侧壁面斜向上运动,并在运动过程中不断发生破碎,形成粒径较小的子气泡。通过两者结果对比,发现实验与模拟得到的气泡破碎形式吻合较好,进一步验证了模拟的准确性。
|
图 11 模拟和实验气泡破碎对比 Fig.11 Comparison on bubble breakup in simulation and experiments |
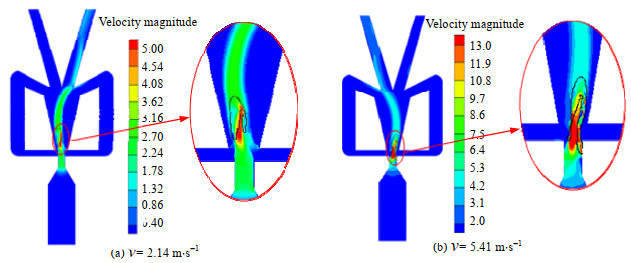
如图 12所示,在流体振荡器局部放大速度云图中,圈出区域表示气相区域。对比喷嘴液速v为2.14和5.41 m⋅s−1的速度分布云图,气泡顶部与底部凹陷部位明显存在较大速度梯度。当v=2.14 m⋅s−1时,气泡顶部与底部速度差达到1.5 m⋅s−1;当v=5.41 m⋅s−1时,气泡顶部与底部速度差接近4.8 m⋅s−1。当速度梯度产生的剪切应力大于气泡表面张力时,气泡就会发生破碎。此外,由于速度梯度增大,气泡边缘会产生大小不一的涡流,涡流碰撞也会增强气泡碎化。
|
图 12 气泡内外区域速度云图 Fig.12 Velocity contours of bubble inside and outside regions |
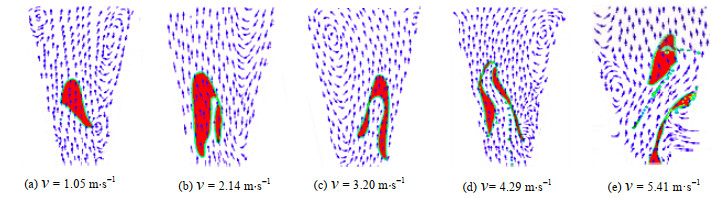
如图 13所示,振荡腔壁面存在大小不一的旋涡,箭头指示了涡流旋转方向。在不同液速下,气泡变形破碎位置均位于旋涡边缘与主射流之间。因为气泡与液体之间存在速度梯度差,加之旋涡碰撞,在二者共同作用下气泡最终碎化成子气泡,并且随着液速增大,气泡变形碎化程度更大。
|
图 13 振荡腔内涡流区域 Fig.13 Eddy current regions in the oscillating cavity |
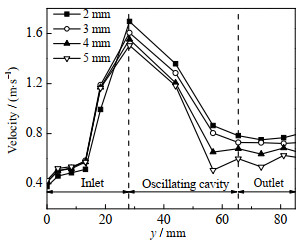
气相流量增加,进入流体振荡器的气泡初始直径随之增大。为研究气泡初始直径对气泡运动的影响,保持v= 2.14 m⋅s−1,待流场稳定后在流体振荡器入口位置注入不同粒径的气泡,气泡初始直径分别为2、3、4、5 mm。如图 14所示,在入口段气泡运动速度均呈先缓慢上升后快速上升趋势,并在振荡腔入口处达到最大速度。气泡从入口到达喷嘴处,流道横截面积缩小,液速增大,因此气泡运动速度随之增大。当气泡从喷嘴进入振荡腔后,液速逐渐降低,气泡也进入减速阶段。随着气泡初始直径增加,气泡运动速度和最大速度均减小。这是因为液速远高于气泡运动速度,初始直径较小的气泡受到液体阻力较小,更容易被液体裹挟前进。
|
图 14 不同气泡初始直径时气泡运动速度 Fig.14 Velocities of bubbles at different initial bubble diameters |
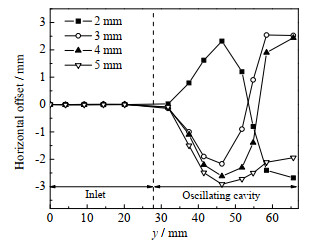
此外,当气泡在振荡腔内运动时,由于流体振荡器中主射流产生周期性振荡,导致射流在振荡腔内来回切换,流场发生偏转并左右振荡,气泡受到振荡流场的影响会向振荡器一侧发生偏转。如图 15所示,当气泡初始直径为2 mm时,水平偏移量为2.32。随着气泡初始直径增加,偏移量逐渐增大。当气泡初始直径达到5 mm,气泡水平偏移量增大到2.91 mm,表明气泡初始直径越大,在振荡腔内的偏移量越大,此时气泡越靠近振荡腔壁面,越容易受到振荡流场的影响而发生破碎。
|
图 15 不同气泡初始直径时气泡水平偏移量 Fig.15 Horizontal offsets of bubbles at different initial bubble diameters |
采用RNG k-ε湍流模型和VOF两相流模型对流体振荡器进行数值模拟,研究了气液两相流中气泡碎化特性,分析得到以下结论:
(1) 设计了长径比为1.1、1.3、1.5和1.85的流体振荡器,对应振荡频率分别为1.67、1.45、1.88、3.7 Hz,表明随着长径比增大,流体振荡器内振荡频率先减后增。通过4种振荡频率下的气泡破碎形式对比,发现振荡频率越高,初始气泡破碎越剧烈,流体振荡器气泡碎化效果越好。
(2) 液速显著影响气泡破碎,当液速较低时,气泡发生变形而未破碎;随着液速增大,气泡变形和碎化程度显著增强,破碎形成的子气泡增多。剪切应力和涡流碰撞是气泡破碎的主导机制。
(3) 流体振荡器产生的射流振荡导致气泡偏移,进而影响气泡运动过程。气泡初始直径越大,水平偏移量越大,气泡越靠近振荡腔壁面,发生破碎概率越高。
| [1] |
王忠, 李甘牛, 陈滨. 一种单出口流体振荡器件特性实验研究[J]. 南京航空航天大学学报, 2015, 47(6): 877-883. WANG Z, LI G N, CHEN B. Experimental investigation on characteristics of single-outlet fluidic oscillators[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2015, 47(6): 877-883. |
| [2] |
刘影, 李春鹏, 张铁军, 等. 后缘连续偏转机翼振荡射流控制的数值模拟研究[J]. 航空科学技术, 2020, 31(5): 36-43. LIU Y, LI C P, ZHANG T J, et al. Numerical simulation of oscillating jet control for trailing edge continuous deflection wing[J]. Aeronautical Science & Technology, 2020, 31(5): 36-43. |
| [3] |
WU Y J, YU S F, ZUO L. Large eddy simulation analysis of the heat transfer enhancement using self-oscillating fluidic oscillators[J]. International Journal of Heat and Mass Transfer, 2019, 131: 463-471. DOI:10.1016/j.ijheatmasstransfer.2018.11.070 |
| [4] |
赵钰, 龚盼, 刘志刚, 等. 新型射流振荡器工作原理与试验研究[J]. 流体机械, 2018, 46(9): 13-17, 83. ZHAO Y, GONG P, LIU Z G, et al. Working principle and experimental research of a new type fluidic oscillator[J]. Fluid Machinery, 2018, 46(9): 13-17, 83. DOI:10.3969/j.issn.1005-0329.2018.09.003 |
| [5] |
HE J F, YIN K, PENG J M, et al. Design and feasibility analysis of a fluidic jet oscillator with application to horizontal directional well drilling[J]. Journal of Natural Gas Science and Engineering, 2015, 27(3): 1723-1731. |
| [6] |
张超. 生物膜反应器内微生物运动及附着特性研究[D]. 重庆: 重庆大学, 2015. ZHANG C. Study on bacterial locomotion and attachment in biofilm reactor [D]. Chongqing: Chongqing University, 2015. |
| [7] |
赵世坤. 集成微流体振荡器的大范围梯度稀释芯片的构建及其在生物学中的应用[D]. 上海: 上海交通大学, 2017. ZHAO S K. A mircofluidic oscillator based long-range gradient generator and its application in biology [D]. Shanghai: Shanghai Jiaotong University, 2017. |
| [8] |
WANG J Y, WANG L G, HANOTU J, et al. Improving the performance of coal flotation using oscillatory air supply[J]. Fuel Processing Technology, 2017, 165: 131-137. DOI:10.1016/j.fuproc.2017.05.022 |
| [9] |
HARUN M H C, ZIMMERMAN W B. Membrane defouling using microbubbles generated by fluidic oscillation[J]. Water Science and Technology: Water Supply, 2019, 19(1): 97-106. DOI:10.2166/ws.2018.056 |
| [10] |
WANG J M, JIN Q Q, ZHANG Y Y, et al. Reducing the membrane fouling in cross-flow filtration using a facile fluidic oscillator[J]. Separation and Purification Technology, 2021, 272: 118854. DOI:10.1016/j.seppur.2021.118854 |
| [11] |
GREGORY J W, TOMAC M N. A review of fluidic oscillator development and application for flow control: 43rd AIAA Fluid Dynamics Conference [C]. San Diego: American Institute of Aeronautics and Astronautics, 2013.
|
| [12] |
HAO Z R, LIU G, WANG Y, et al. Studies on the drive mechanism of the main jet deflection inside a fluidic oscillator[J]. Industrial & Engineering Chemistry Research, 2020, 59(20): 9629-9641. |
| [13] |
别海燕, 黄晨, 安维中, 等. 正反馈式流体振荡器内部流动特性的数值模拟[J]. 化工学报, 2021, 72(3): 1504-1511. BIE H Y, HUANG C, AN W Z, et al. Numerical simulation of the internal flow characteristics in a feedback fluidic oscillator[J]. CIESC Journal, 2021, 72(3): 1504-1511. |
| [14] |
MING T Z, WANG Z Y, LIAO X W, et al. Unsteady RANS simulation of fluid dynamic and heat transfer in an oblique self-oscillating fluidic oscillator array[J]. International Journal of Heat and Mass Transfer, 2021, 177: 121515. DOI:10.1016/j.ijheatmasstransfer.2021.121515 |
| [15] |
PANDEY R J, KIM K Y. Numerical modeling of internal flow in a fluidic oscillator[J]. Journal of Mechanical Science and Technology, 2018, 32(3): 1041-1048. DOI:10.1007/s12206-018-0205-x |
| [16] |
ZHENG J G, XIA L, HU J, et al. Numerical investigation of characteristics of fluidic oscillator operating in quiescent air and a crossflow[J]. Aerospace Science and Technology, 2021, 113(3): 106731. |
| [17] |
TESAŘ V. Fluidic oscillators mediating generation of microbubbles (Survey)[J]. Fluids, 2021, 6(2): 77. DOI:10.3390/fluids6020077 |
| [18] |
李辉, 李干禄, 何峰, 等. 微气泡耦合生物反应器的研究进展[J]. 化工进展, 2020, 39(12): 4758-4765. LI H, LI G L, HE F, et al. Research progress of microbubble coupled bioreactor[J]. Chemical Industry and Engineering Progress, 2020, 39(12): 4758-4765. |
| [19] |
冯俊杰, 孙冰, 姜杰, 等. 射流场中单个气泡破裂的CFD模拟与PIV实验研究[J]. 高校化学工程学报, 2018, 32(2): 286-294. FENG J J, SUN B, JIANG J, et al. CFD simulation and PIV investigation on single bubble breakup in turbulent jet flow[J]. Journal of Chemical Engineering of Chinese Universities, 2018, 32(2): 286-294. |
| [20] |
MOVAHED S, SARMAH A K. Global trends and characteristics of nano- and micro-bubbles research in environmental engineering over the past two decades: A scientometric analysis[J]. Science of the Total Environment, 2021, 785: 147362. |
| [21] |
HUANG Z L, CHEN Q Y, YAO Y, et al. Micro-bubbles enhanced removal of diesel oil from the contaminated soil in washing/flushing with surfactant and additives[J]. Journal of Environmental Management, 2021, 290: 112570. |
| [22] |
LACERDA Q, TANTAWI M, LEEPER D B, et al. Emerging applications of ultrasound-contrast agents in radiation therapy[J]. Ultrasound in Medicine & Biology, 2021, 47(6): 1465-1474. |
| [23] |
UESAWA S, KANEKO A, NOMURA Y, et al. Fluctuation of void fraction in the microbubble generator with a venturi tube: ASME-JSME-KSME 2011 Joint Fluids Engineering Conference [C]. Hamamatsu: Japanese Society of Mechanical Engineers, 2011.
|




