2. 桂林理工大学 信息科学与工程学院, 广西 桂林 541006
2. Institute of Information Science and Engineering, Guilin University of Technology, Guilin 541006, China
氯氟烃和氢氯氟烃等传统制冷剂,因具备较高全球变暖潜能值(GWP)和臭氧消耗值(ODP)逐渐被新兴制冷剂淘汰[1]。天然制冷剂CO2,无毒不易燃,化学性质稳定,单位容积制冷量大[2-4],其ODP为零且GWP极小[5-6]。离子液体(ILs)作为由不同阴阳离子组成的绿色溶液,具有较高的化学稳定性、热稳定性、气体溶解能力和分子结构可设计性[7-8],研究发现多数离子液体对CO2有较高吸收能力[9-11]。Morgan等[12-13]研究发现温度为293.15~363.15 K、压力为0.1~50 MPa时,CO2在[emim][Tf2N]中的溶解度高达0.8 mol·L−1。He等[14]研究发现温度为283.15~363.15 K、压力为0.2~5 MPa时,CO2在[BMP][Tf2N]中的摩尔溶解度最高可达0.532 4 mol·L−1。众多研究表明ILs可作为良好的CO2吸收剂,应用于吸收式制冷循环系统装置中[15-16]。
很多学者对不同CO2-ILs体系的汽液相平衡进行实验研究,得到不同温度、压力下CO2-ILs体系的相平衡数据[17-19]。以相平衡数据为基础,选择合适的模型可预测热力学性质[20-21]。王卫[22]测定了CO2-[omim][BF4]、CO2-[omim][Tf2N]的汽液相平衡数据,通过UNIFAC模型预测了相平衡时CO2的溶解度,平均相对偏差分别为2.54%、3.87%。何丽娟等[3]用PR+NRTL方法关联Schilderman等的实验数据,得出CO2和[emim][Tf2N]二元混合体系在高温高压下的超额混合焓,表明CO2液相摩尔分数大于0.43时体系的超额混合焓均为负值,混合为放热过程。胡艺等[23]通过实验测定离子液体的吸收焓,发现CO2与离子液体之间的相互作用受二者之间形成的键长、键角影响。Safarov等[24]测定了CO2在离子液体[emim][CH3SO3]中的溶解度,根据亨利定律常数关联出混合物的溶解吉布斯自由能、溶解焓和溶解熵。溶解焓和溶解熵均为负值,表明CO2溶于离子液体时存在放热过程且溶液有序性较高。众多研究表明,热力学性质对于研究CO2及其他气体在离子液体中的溶解度具有重要的参考价值。
目前许多学者致力于研究CO2-ILs体系的吉布斯自由能等性质,但相关的超额性质研究较少。为了进一步研究不同类别的CO2-ILs二元体系相平衡特性和热力学性质,本研究选取阴离子相同、阳离子烷基链长度不同的4种离子液体([C2-mim][Tf2N]、[C4-mim][Tf2N]、[C6-mim][Tf2N]、[C8-mim][Tf2N]),整理了Shin等[17]的实验数据,采用SRK状态方程+WS混合规则+UNIFAC活度系数模型,探究了温度、压力、CO2溶解度和ILs阳离子烷基链长度对混合体系超额吉布斯自由能、超额焓、超额熵的影响。
2 热力学模型 2.1 SRK状态方程SRK状态方程[25]如下所示:
| $ p = \frac{{RT}}{{{V_{\text{m}}} - b}} - \frac{a}{{{V_{\text{m}}}({V_{\text{m}}} + b)}} $ | (1) |
| $ a = {a_{\text{c}}}\alpha ({T_{\text{r}}},\omega ) $ | (2) |
| $ {a_{\text{c}}} = {0.427_{}}48\frac{{{R^2}T_{\text{c}}^2}}{{{p_{\text{c}}}}} $ | (3) |
| $ b = {0.086_{}}64\frac{{R{T_{\text{c}}}}}{{{p_{\text{c}}}}} $ | (4) |
| $ {\alpha ^{0.5}} = 1 + \left( {0.48 + 1.574\omega - 0.176{\omega ^2}} \right)\left( {1 - T_{\text{r}}^{0.5}} \right) $ | (5) |
式中:Vm为摩尔体积,m3·mol−1;p为压力,Pa;
|
|
表 1 纯物质的临界性质表 Table 1 Critical properties of pure substances |
WS混合规则[26]如下所示:
| $ {a_{\text{m}}} = {b_{\text{m}}}RTD $ | (6) |
| $ {b_{\text{m}}} = \frac{Q}{{1 - D}} $ | (7) |
| $ D = \sum\limits_i {\frac{{{a_i}}}{{{b_i}RT}}} + \frac{1}{C}\frac{{{G^{\text{E}}}}}{{RT}} $ | (8) |
| $ Q = \sum\limits_i {\sum\limits_j {{x_i}{x_j}{{(b - \frac{a}{{RT}})}_{ij}}} } $ | (9) |
| $ {(b - \frac{a}{{RT}})_{ij}} = \frac{1}{2}({b_i} + {b_j}) - \frac{{\sqrt {{a_i}{a_j}} }}{{RT}}(1 - {k_{ij}}) $ | (10) |
式中:D为介电常数;
Fredenslund等[27]基于量子化学理论(UNIQUAC)和基团贡献概念提出UNIFAC模型。Lei等[28]对UNIFAC模型进行了改进。该模型由组合项和剩余项组成,其中组合项
| $ \ln {\gamma _i} = \ln \gamma _i^{\text{c}} + \ln \gamma _i^{\text{R}} $ | (11) |
| $ 组合项:\ln \gamma _i^{\text{c}} = \ln \frac{{{\varphi _i}}}{{{x_i}}} + \frac{Z}{2}{q_i}\ln \frac{{{\theta _i}}}{{{\varphi _i}}} + {l_i} - \frac{{{\varphi _i}}}{{{x_i}}}\sum\limits_j {{x_j}} {l_j} $ | (12) |
| $ {l_i} = \frac{Z}{2}({r_i} - {q_i}) - ({r_i} - 1){,_{}}Z = 10 $ | (13) |
| $ {\theta _i} = \frac{{{q_i}{x_i}}}{{\sum\limits_j {{q_j}{x_j}} }} \text{ } {\varphi _i} = \frac{{{v_i}{x_i}}}{{\sum\limits_j {{v_j}{x_j}} }} $ | (14) |
| $ {r_i} = \sum\limits_k {v_k^{(i)}} {R_k} \text{ } {q_i} = \sum\limits_k {v_k^{(i)}} {Q_k} $ | (15) |
式中:
| $ 剩余项:\ln \gamma _i^{\text{R}} = \sum\limits_k {v_k^{(i)}} (\ln {\mathit{\Gamma } _k} - \ln \mathit{\Gamma } _k^{(i)}) $ | (16) |
| $ \ln {\mathit{\Gamma } _k} = {Q_k}[1 - {\ln _{}}(\sum\limits_m {{\mathit{\Theta } _m}{\mathit{\Psi } _{mk}}} ) - \sum\limits_m {(\frac{{{\mathit{\Theta } _m}{\mathit{\Psi } _{mk}}}}{{\sum\limits_n {{\mathit{\Theta } _n}{\mathit{\Psi } _{nm}}} }}} )] $ | (17) |
| $ \ln \mathit{\Gamma } _k^{(i)} = {Q_k}[1 - {\ln _{}}(\sum\limits_m {\mathit{\Theta } _m^{(i)}} {\mathit{\Psi } _{mk}}) - \sum\limits_m {\frac{{\mathit{\Theta } _m^{(i)}{\mathit{\Psi } _{km}}}}{{\sum\limits_n {\mathit{\Theta } _m^{(i)}{\mathit{\Psi } _{nm}}} }}} ] $ | (18) |
式中:Гk为k基团的剩余活度系数,
| $ {\mathit{\Psi } _{nm}} = {\exp _{}}(\frac{{ - {a_{mn}}}}{T}) $ | (19) |
式中:
UNIFAC活度系数模型用于离子液体,目前常用的拆分方法有3种。本研究采用Lei等[28]的拆分方式,将离子液体[C2-mim][Tf2N]的阴阳离子看作一个整体(即[−mim][Tf2N],这样可忽略阴阳离子间的静电作用),将阳离子的烷基链(丁基)拆成1个─CH3,1个─CH2 ([C4-mim][Tf2N]、[C6-mim][Tf2N]、[C8-mim][Tf2N]拆分方法类似,拆分示意图如图 1所示)。各个基团间的相互作用参数采用Lei等[28]回归得到的UNIFAC活度系数模型相互作用参数。
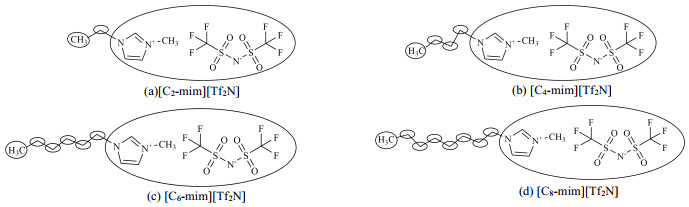
|
图 1 [Cn-mim][Tf2N](n=2, 4, 6, 8)拆分示意图 Fig.1 Chemical structural diagram of [Cn-mim][Tf2N](n=2, 4, 6, 8) |
对于二元混合体系汽液相平衡准则:
| $ \hat f_i^{\text{v}} = \hat f_i^{\text{l}} $ | (20) |
汽相和液相组分逸度分别用组分逸度系数和活度系数来计算,平衡关系式如下:
| $ p\hat \varphi _i^{\text{v}}{y_i} = f_i^{\text{l}}{x_i}{\gamma _i} $ | (21) |
式中:
本研究采用状态方程+活度系数(EOS+γ)法计算了4组CO2-ILs体系的相平衡数据。图 2是EOS+γ法计算CO2-ILs体系相平衡数据的流程图。通过迭代计算压力值,使气相组成归一化条件成立,结束迭代,输出结果。
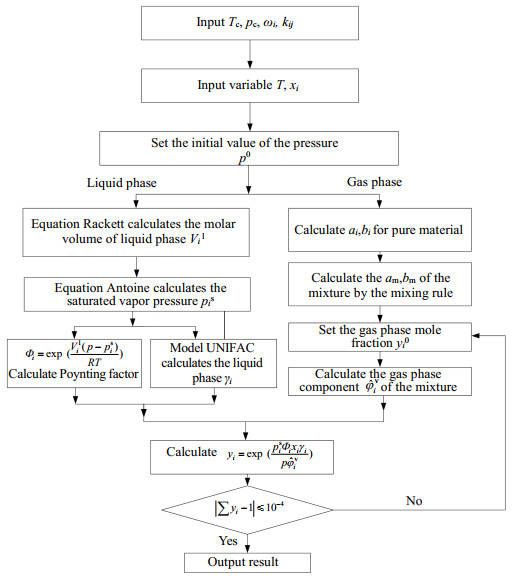
|
图 2 汽液相平衡计算流程图 Fig.2 Flow chart of vapor-liquid equilibrium calculation |
通过整理Shin等[17]的汽液相平衡实验数据,计算了4组CO2-ILs体系的相平衡数据,并关联了该体系的超额热力学性质。4组CO2-ILs二元体系相平衡实验数据及计算数据见表 2。表中pcal是通过迭代气泡点压力得到的计算值,pexp是实验值,x为CO2在液相中的摩尔分数。将GE的定义与
| $ \frac{{{G^{\text{E}}}}}{{RT}} = \sum\limits_i {{x_i}\ln {\gamma _i}} $ | (22) |
|
|
表 2 CO2-[Cn-min][Tf2N](n=2, 4, 6, 8)体系VLE数据 Table 2 VLE measurement results of the CO2-[Cn-min][Tf2N](n=2, 4, 6, 8) system |
由GE,可得到超额焓HE与超额熵SE:
| $ {H^{\text{E}}} = - {T^2}\left( {\frac{{\partial \left( {\frac{{{G^{\text{E}}}}}{T}} \right)}}{{\partial T}}} \right) $ | (23) |
| $ {S^{\text{E}}} = \frac{{{H^{\text{E}}} - {G^{\text{E}}}}}{T} = - \left( {\frac{{\partial {G^{\text{E}}}}}{{\partial T}}} \right) $ | (24) |
利用SRK状态方程、WS混合规则以及UNIFAC活度系数模型得到GE的计算结果如图 3所示。

|
图 3 CO2-[Cn-mim][Tf2N](n=2, 4, 6, 8)体系的超额吉布斯自由能 Fig.3 Excess Gibbs free energy of the CO2-[Cn-mim][Tf2N](n=2, 4, 6, 8) system |
由图 3可知:当CO2液相摩尔分数为定值时,CO2-[Cn-mim][Tf2N](n=2, 4, 6, 8)型二元混合体系的GE分别随温度、压力和ILs阳离子烷基链长度增大而减小。其中压力对GE影响较大。当x=0.233、ILs阳离子碳基链长度n=2时,GE出现最大值,为−1 066.88 J·mol−1。
随着CO2液相摩尔分数的增加,GE受温度影响减弱。ILs密度随温度的升高而减小,自由体积增大,吸附CO2的能力增强,同时自由体积随CO2液相摩尔分数的增大而减小,GE的变化趋于平缓。随着ILs烷基链长度递增,自由体积增大,GE的数值随之增大。
3.1.2 超额焓HE的结果分析利用SRK状态方程、WS混合规则以及UNIFAC活度系数模型得到HE的计算结果如图 4所示。
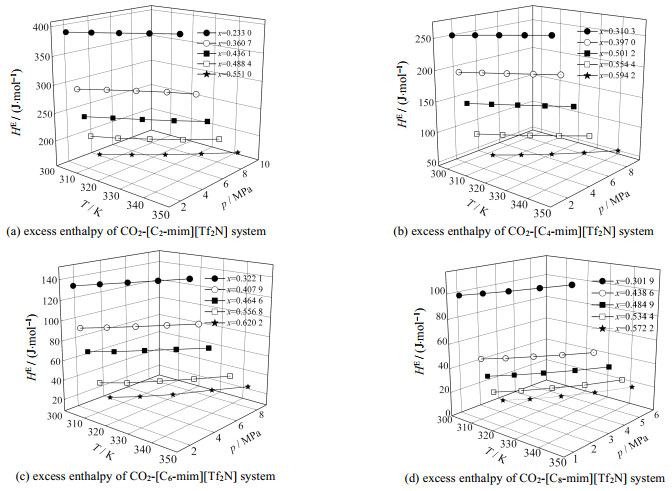
|
图 4 CO2-[Cn-mim][Tf2N](n=2, 4, 6, 8)体系的超额焓 Fig.4 Excess enthalpy of the CO2-[Cn-mim][Tf2N](n=2, 4, 6, 8) system |
由图 4可知,当CO2摩尔分数为定值时,CO2-[Cn-mim][Tf2N](n=2, 4, 6, 8)型二元混合体系的超额焓HE受温度和压力的影响较小。HE随ILs阳离子烷基链长度、CO2摩尔分数的增大而减小,其中CO2摩尔分数对混合体系超额焓影响较大。当x=0.233、ILs阳离子烷基链长度n=2时,HE出现最大值,为407.24 J·mol−1。
HE受黏度影响较大,混合体系的黏度由分子间氢键和范德华力决定,随着ILs阳离子烷基链长度和CO2液相摩尔分数增大,烷基链与CO2之间形成新的分子间作用力,HE随之减小。
3.1.3 超额熵SE的结果分析利用SRK状态方程、WS混合规则以及UNIFAC活度系数模型得到SE的计算结果如图 5所示。
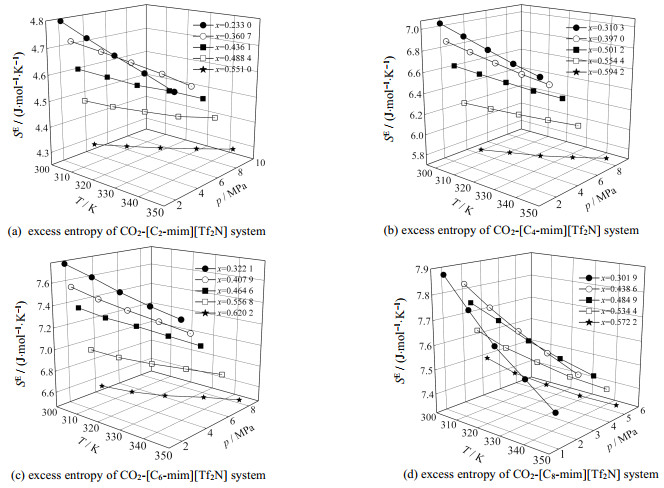
|
图 5 CO2-[Cn-mim][Tf2N](n=2, 4, 6, 8)体系的超额熵 Fig.5 Excess entropy of the CO2-[Cn-mim][Tf2N](n=2, 4, 6, 8) system |
由图 5可知,当CO2摩尔分数为定值时,SE随ILs阳离子烷基链长度的增大而增大,随压力的增大而减小。随着CO2摩尔分数增大,温度对超SE的影响逐渐减小。当x=0.301 9、ILs阳离子烷基链长度n=8时,SE出现最大值,7.88 J·mol−1·K−1。
SE代表真实溶液与理想溶液的熵的偏差。随着ILs阳离子烷基链长度的增大,混合体系的有序性降低。随着CO2摩尔分数增大,温度和压力对溶液有序性的影响逐渐减小。
3.2 相互作用参数kij回归及模型精确度计算kij影响相平衡模型的精确度,kij不同,迭代计算输出压力值也不同。为使模型预测效果更加精准,通过目标函数OF(式(25)),对CO2-[Cn-mim][Tf2N](n=2, 4, 6, 8)型二元混合体系的kij进行回归。当OF计算结果取最小值时,输出此时的kij。计算结果显示,ILs阳离子烷基链长度n=2, 4, 6, 8时,二元混合体系的kij分别为0.42、0.51、0.60和0.62时,模型的计算误差最小,此时压力p的平均相对偏差ARD(式(26))如表 3所示。随着温度升高,CO2-ILs体系压力p的平均相对偏差ARD逐渐增大,模型预测精度逐渐降低;当温度为定值时,随着ILs阳离子烷基链的增加,压力p的ARD逐渐减小,模型预测精度逐渐升高。同时随着ILs阳离子烷基链的增加,CO2与[Cn-mim][Tf2N]的相互作用参数逐渐增大。
| $ \text{OF} = \sum\limits_{q = 1}^{{N_{\text{E}}}} {{{\left( {\frac{{p_q^{\exp } - p_q^{\text{cal}}}}{{p_q^{\exp }}}} \right)}^{\text{2}}}} $ | (25) |
| $ \text{ARD} = \frac{1}{N}\sum\limits_{q = {\text{1}}}^N {\frac{{\left| {p_q^{\exp } - p_q^{\text{cal}}} \right|}}{{p_q^{\exp }}}} $ | (26) |
|
|
表 3 CO2-[Cn-mim][Tf2N](n=2, 4, 6, 8)二元体系压力的ARD Table 3 Pressure ARD values of the CO2-[Cn-mim][Tf2N](n=2, 4, 6, 8) binary system |
式中:NE为系统实验数据组数。
由表 3知,SRK+WS+UNIFAC模型计算CO2-[Cn-mim][Tf2N](n=2, 4, 6, 8)型二元混合体系具有较高精度。ILs阳离子烷基链长度越长,SRK+WS+UNIFAC模型的计算精度越高,同时该模型的精度受压力影响较大。4种离子液体的极性都随着阳离子上烷基链长度的增加而减小[30],因此SRK+WS+UNIFAC模型更适合计算温度压力较低、极性较弱的CO2-ILs体系。
4 结论采用选定状态方程+活度系数法计算了CO2-[Cn-mim][Tf2N](n=2, 4, 6, 8) 4种混合工质对的相平衡,得出以下结论:
(1) 超额吉布斯自由能GE随温度、压力、ILs烷基链长度增大呈下降趋势,受压力影响变化较大。
(2) 超额焓HE受温度、压力的影响较小,受CO2摩尔分数影响较大,随ILs阳离子烷基链长度的增加而减小。
(3) 超额熵SE随ILs阳离子烷基链长度的增大而增大,随着压力的升高而减小。
(4) SRK+WS+UNIFAC模型对CO2-[Cn-mim][Tf2N](n=2, 4, 6, 8)型二元混合体系具有较高计算精度。
| [1] |
United Nations Environment Programme. 2018 Report of the refrigeration, air conditioning and heat pumps technical options committee [R]. Kenya United Nations Environment Programme, 2019.
|
| [2] |
彭丽, 武卫东, 吴俊, 等. 基于K-K方程的CO2-离子液体吸收制冷工质对相平衡特性预测[J]. 高校化学工程学报, 2019, 33(2): 274-282. PENG L, WU W D, WU J, et al. Prediction of phase equilibrium characteristics of CO2-ionic liquid working pairs based on K-K equation[J]. Journal of Chemical Engineering of Chinese Universities, 2019, 33(2): 274-282. DOI:10.3969/j.issn.1003-9015.2019.02.003 |
| [3] |
何丽娟, 梁晶晶, 张少华. CO2-[emim][Tf2N]二元混合体系超额混合焓的预测[J]. 西安交通大学学报, 2015, 49(9): 99-104. HE L J, LIANG J J, ZHANG S H. Prediction of molar excess enthalpies in binary solution of CO2-[emim][Tf2N][J]. Journal of Xi'an Jiaotong University, 2015, 49(9): 99-104. |
| [4] |
孙建军. 二氧化碳跨临界两级压缩制冷系统性能研究[D]. 天津: 天津商业大学, 2019. SUN J J. Study on the performances of CO2 transcritical two-stage compression refrigeration system [D]. Tianjin: Tianjin University of Commerce, 2019. |
| [5] |
许文华, 李惟毅, 郭强. 考虑环境影响的CO2/低GWP混合工质热泵热水器工质优选[J]. 太阳能学报, 2018, 39(1): 84-89. XU W H, LI W Y, GUO Q. Working fluids selecting of CO2 blends with low-GWP(Global Warming Potential) heat pump system considering impact of environment[J]. Acta Energiae Solaris Sinica, 2018, 39(1): 84-89. |
| [6] |
何丽娟, 马文清, 孙尚志, 等. CO2-[emim][Tf2N]二元体系汽液相平衡及超额焓研究[J]. 高校化学工程学报, 2020, 34(3): 603-610. HE L J, MA W Q, SUN S Z, et al. Vapor-liquid equilibrium and excess enthalpy of the CO2-[emim][Tf2N] binary system[J]. Journal of Chemical Engineering of Chinese Universities, 2020, 34(3): 603-610. DOI:10.3969/j.issn.1003-9015.2020.03.006 |
| [7] |
COGNIGNI A, KAMPICHLER S, BICA K. Surface-active ionic liquids in catalysis: Impact of structure and concentration on the aerobic oxidation of octanol in water[J]. Journal of Colloid and Interface Science, 2017, 492: 136-145. DOI:10.1016/j.jcis.2016.12.063 |
| [8] |
吴建猛, 郑爽, 曾少娟, 等. 负载型离子液体吸附分离CO2的研究现状及展望[J]. 化工学报, 2022, 73(10): 4268-4284. WU J M, ZHENG S, ZENG S J, et al. Status and prospect on CO2 adsorption and separation by supported ionic liquids[J]. CIESC Journal, 2022, 73(10): 4268-4284. |
| [9] |
ANTHONY J L, MAGINN E J, BRENNECKE J F. Solubilities and thermodynamic properties of gases in the ionic liquid 1-n-butyl-3-methylimidazolium hexafluorophosphate[J]. The Journal of Physical Chemistry B, 2002, 106(29): 7315-7320. DOI:10.1021/jp020631a |
| [10] |
ZHAO Y S, ZHANG X P, DONG H F, et al. Solubilities of gases in novel alcamines ionic liquid 2-[2-hydroxyethyl (methyl) amino] ethanol chloride[J]. Fluid Phase Equilibria, 2011, 302(1/2): 60-64. |
| [11] |
BARA J E, CARLISLE T K, GABRIEL C J, et al. Guide to CO2 separations in imidazolium-based room-temperature ionic liquids[J]. Industrial & Engineering Chemistry Research, 2009, 48(6): 2739-2751. |
| [12] |
MORGAN D, FERGUSON L, SCOVAZZO P. Diffusivities of gases in room-temperature ionic liquids: Data and correlations obtained using a lag-time technique[J]. Industrial & Engineering Chemistry Research, 2005, 44(13): 4815-4823. |
| [13] |
CARVALHO P J, ÁLVAREZ V H, MACHADO J J B, et al. High pressure phase behavior of carbon dioxide in 1-alkyl-3-methylimidazolium bis (trifluoromethylsulfonyl) imide ionic liquids[J]. The Journal of Supercritical Fluids, 2009, 48(2): 99-107. DOI:10.1016/j.supflu.2008.10.012 |
| [14] |
HE L J, YANG W X, HAN Y Z, et al. Vapor-liquid equilibrium experiment and prediction of excess property of new working pair CO2-[Tf2N] in absorption refrigeration system[J]. International Journal of Refrigeration, 2023, 145: 407-416. DOI:10.1016/j.ijrefrig.2022.09.031 |
| [15] |
张文林, 陈瑶, 高展艳, 等. 功能化碱性离子液体在吸收CO2领域的研究进展[J]. 现代化工, 2017, 37(2): 41-45, 47. ZHANG W L, CHEN Y, GAO Z Y, et al. Progress of functionalized ionic liquids for CO2 absorption[J]. Modern Chemical Industry, 2017, 37(2): 41-45, 47. |
| [16] |
吴夏梦. [BMP][Tf2N]离子液体基础物性及CO2溶解度的实验研究[D]. 包头: 内蒙古科技大学, 2020. WU X M. Experiment Study on [BMP][Tf2N] ionic liquid basic physical properties and CO2 solubility characteristic [D]. Baotou: Inner Mongolia University of Science & Technology, 2020. |
| [17] |
SHIN E K, LEE B C, LIM J S. High-pressure solubilities of carbon dioxide in ionic liquids: 1-alkyl-3-methylimidazolium bis (trifluoromethylsulfonyl) imide[J]. The Journal of Supercritical Fluids, 2008, 45(3): 282-292. DOI:10.1016/j.supflu.2008.01.020 |
| [18] |
ZENG S J, WANG J, BAI L, et al. Highly selective capture of CO2 by ether-functionalized pyridinium ionic liquids with low viscosity[J]. Energy & Fuels, 2015, 29(9): 6039-6048. |
| [19] |
YIM J H, SONG H N, LEE B C, et al. High-pressure phase behavior of binary mixtures containing ionic liquid [HMP][Tf2N], [OMP][Tf2N] and carbon dioxide[J]. Fluid Phase Equilibria, 2011, 308(1/2): 147-152. |
| [20] |
VEGA L F, VILASECA O, LLOVELL F, et al. Modeling ionic liquids and the solubility of gases in them: Recent advances and perspectives[J]. Fluid Phase Equilibria, 2010, 294(1/2): 15-30. |
| [21] |
张双. 离子液体对两种共沸物系汽液相平衡的研究及其模型化[D]. 北京: 北京化工大学, 2015. ZHANG S. The study on effects and modeling of ionic liquids for two azeotropic systems [D]. Beijing: Beijing University of Chemical Technology, 2015. |
| [22] |
王卫. UNIFAC模型用于离子液体-气体体系的研究[D]. 北京: 北京化工大学, 2013. WANG W. UNIFAC model for ionic liquid-gas systems [D]. Beijing: Beijing University of Chemical Technology, 2013. |
| [23] |
胡艺. 常规咪唑离子液体吸收CO2的热力学性能研究[D]. 武汉: 华中科技大学, 2018. HU Y. Experimental investigation of co2 absorption thermodynamic performance in conventional imidazole-based ionic liquids [D]. Wuhan: Huazhong University of Science and Technology, 2018. |
| [24] |
SAFAROV J, ABDULLAYEVA G, BASHIROV M, et al. The ionic liquid 1-ethyl-3-methylimidazolium methanesulfonate revisited: Solubility of carbon dioxide over an extended range of temperature and pressure[J]. Journal of Molecular Liquids, 2021, 333: 115920. DOI:10.1016/j.molliq.2021.115920 |
| [25] |
SOAVE G. Equilibrium constants from a modified Redlich-Kwong equation of state[J]. Chemical Engineering Science, 1972, 27(6): 1197-1203. |
| [26] |
WONG D S H, SANDLER S I. A theoretically correct mixing rule for cubic equations of state[J]. AIChE Journal, 1992, 38(5): 671-680. |
| [27] |
FREDENSLUND A, JONES R L, PRAUSNITZ J M. Group-contribution estimation of activity coefficients in nonideal liquid mixtures[J]. AIChE Journal, 1975, 21(6): 1086-1099. |
| [28] |
LEI Z G, ZHANG J G, LI Q S, et al. UNIFAC model for ionic liquids[J]. Industrial & Engineering Chemistry Research, 2009, 48(5): 2697-2704. |
| [29] |
SHIFLETT M B, YOKOZEKI A. Solubility and diffusivity of hydrofluorocarbons in room-temperature ionic liquids[J]. AIChE Journal, 2006, 52(3): 1205-1219. |
| [30] |
DAGUENET C, DYSON P J, KROSSING I, et al. Dielectric response of imidazolium-based room-temperature ionic liquids[J]. The Journal of Physical Chemistry B, 2006, 110(25): 12682-12688. |




