2. 山东科技大学 经济管理系,山东 泰安 271000
2. Department of Economic and Management,Shandong University of Science and Technology,Tai'an 271000,China
危险和可操作性分析(Hazard and Operability,简称HAZOP),由英国帝国化学工业公司(ICI)首先提出,主要用于分析、查找、预测化工过程中的设计缺陷、操作规程缺陷及其它可能存在的隐患。传统HAZOP分析是一种费时、费力的完全依靠知识和经验的脑力活动[1]。
1980年计算机辅助HAZOP分析系统的研究就已经开始,初期以文字记录类软件为主,直到上世纪90年代,相对成熟的智能HAZOP分析方法才出现。先后开发出的智能化HAZOP定性分析方法有QHI系统[2]、 HAZOPExpert系统[3]、 PHASuite系统[4, 5]、HELPHAZOP系统[6]、 EXPERTOP系统[7]。这些HAZOP定性分析方法将所有偏离正常值的系统参数都定义为偏差,没有“量”的概念,即使有些偏差不会造成危险后果也会包含在内,导致分析结果不准确,并且增加了分析报告的冗余度。为改善之,许多学者开始尝试研究定量分析,提出了HAZOP定性分析与定量分析相结合的方法[8~11]、HAZOP分析与过程模拟相结合的方法[12~18],通过以上方法可以确定偏差的安全范围,但是基于偏差产生后数值保持不变的假设,即分析某一工艺参数的n个不同数值的偏差对系统的影响,从而确定偏差的安全范围,本质是重复n次稳态模拟。在实际生产中,偏差一般不会保持恒定而不变化,此种情况虽然可以利用HAZOP分析与动态模拟相结合的方法加以研究,但是需要对偏差“一变化一模拟”,偏差有无限种变化,模拟需要做无限次,仅靠动态模拟确定具有无限种变化的“动态偏差”的安全范围非常困难。本文提出在有限次的稳态模拟基础上,利用“基于动态偏差的智能化HAZOP量化分析”解决此困难,确定“动态偏差”的安全范围。
另外,Huang[12]研究了偏差持续时间不同,偏差的安全范围不同;石艳娟等在文献中利用HYSYS动态模拟调节阀故障,确定阀位限制在30% 左右,并在20 min内及时做出调整,以免液位继续升高造成事故[18]。从而明确了偏差对系统的影响不仅取决于偏差的数值,而且与偏差持续时间有关。因此,只用偏差的数值大小判断是否会引起系统危险,存在片面性,只有当偏差的持续时间超过某一限值后,才会引起系统危险。本文提出以持续时间限值划分偏差的不同范围,以持续时间是否达到限值作为是否引起系统危险的判断依据,研究动态偏差对系统的影响。
2 动态偏差定义及其对系统的影响 2.1 动态偏差定义在传统HAZOP中偏差为引导词加工艺参数组合而成[19],不涉及持续时间。而在实际的生产过程中,正常的工艺参数一般要设定在某一特定的区间范围,一旦发生了工艺参数的偏差,由于偏差累积和工艺调节,偏差是极易随时间变化的,即偏差具有动态性。本文将数值随时间发生变化的偏差称为动态偏差。对应地将数值不随时间变化的偏差称为稳态偏差。
为了研究偏差数值大小随时间发生的变化及持续时间对系统的影响,本文提出了“动态偏差”的概念,将动态偏差定义为持续时间
根据偏差引起系统危险所需要的时间不同,
当
过程系统动态模拟一般可表示为:
| $\frac{\partial y}{\partial t}=f\left( x \right)$ | (1) |
其中,
设系统的初始条件为:
| $y=f\left( x \right)\left( t-{{t}_{0}} \right)+{{y}_{0}}$ | (2) |
当系统初始状态是偏差产生时刻时,
| $y=f\left( x \right){{t}^{d}}+{{y}_{0}}$ | (3) |
设系统出现危险时刻时输出变量为
| $Y=f\left( x \right){{t}^{\lim }}+{{y}_{0}}$ | (4) |
设
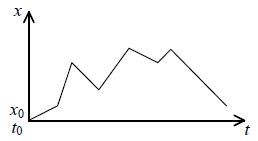
|
图 1 偏差数值随时间变化示意图 Fig.1 Schematic diagram of deviation value profile as a function of time |
| $\left\{ \begin{matrix} {{y}_{1}}=f\left( {{x}_{1}} \right)t_{1}^{d}+{{y}_{0}} \\ {{y}_{2}}=f\left( {{x}_{2}} \right)t_{2}^{d}+{{y}_{1}} \\ \vdots \\ {{y}_{n}}=f\left( {{x}_{n}} \right)t_{n}^{d}+{{y}_{n-1}} \\ \end{matrix} \right.$ | (5) |
和
| $\left\{ \begin{matrix} Y=f\left( {{x}_{1}} \right)t_{1}^{\lim }+{{y}_{0}} \\ Y=f\left( {{x}_{2}} \right)t_{2}^{\lim }+{{y}_{0}} \\ \vdots \\ Y=f\left( {{x}_{n}} \right)t_{n}^{\lim }+{{y}_{0}} \\ \end{matrix} \right.$ | (6) |
由方程组(5) 得:
| ${{y}_{n}}=f\left( {{x}_{n}} \right)t_{n}^{d}+f\left( {{x}_{n-1}} \right)t_{n-1}^{d}+\cdots +f\left( {{x}_{1}} \right)t_{1}^{d}+{{y}_{0}}$ | (7) |
由方程组(6) 得:
| $\left\{ \begin{matrix} f\left( {{x}_{1}} \right)=f\left( {{x}_{n}} \right)\frac{t_{n}^{\lim }}{t_{1}^{\lim }} \\ f\left( {{x}_{2}} \right)=f\left( {{x}_{n}} \right)\frac{t_{n}^{\lim }}{t_{2}^{\lim }} \\ \vdots \\ f\left( {{x}_{n-1}} \right)=f\left( {{x}_{n}} \right)\frac{t_{n}^{\lim }}{t_{n-1}^{\lim }} \\ \end{matrix} \right.$ | (8) |
将方程组(8) 代入式(7) 得:
| ${{y}_{n}}=f\left( {{x}_{n}} \right)\left[ \left( \frac{t_{1}^{d}}{t_{1}^{lim}}+\frac{t_{2}^{d}}{t_{1}^{lim}}+\cdots +\frac{t_{n}^{d}}{t_{m}^{lim}} \right)t_{n}^{lim} \right]+{{y}_{0}}$ | (9) |
即
| ${{y}_{n}}=t_{n}^{\lim }\sum\limits_{i=1}^{n}{\frac{t_{i}^{d}}{t_{i}^{\lim }}}f\left( {{x}_{n}} \right)+{{y}_{0}}$ | (10) |
由式(10) 知:当
由以上分析可以看出,动态偏差对系统的影响可以借助稳态偏差加以分析,式(10) 可以定义
| $t_{e}^{d}\text{ = }t_{n}^{\lim }\sum\limits_{i=1}^{n}{\frac{t_{i}^{d}}{t_{i}^{\lim }}}$ | (11) |
动态偏差引起系统发生危险满足的条件由式(9) 可知:
| $\frac{t_{n}^{\lim }}{t_{1}^{\lim }}t_{1}^{d}+\frac{t_{n}^{\lim }}{t_{2}^{\lim }}t_{2}^{d}+\cdots +\frac{t_{n}^{\lim }}{t_{n-1}^{\lim }}t_{n-1}^{d}\text{+}t_{n}^{d}\text{ = }t_{n}^{\lim }$ | (12) |
设$\frac{t_{n}^{\lim }}{t_{1}^{\lim }}t_{1}^{d}+\frac{t_{n}^{\lim }}{t_{2}^{\lim }}t_{2}^{d}+\cdots +\frac{t_{n}^{\lim }}{t_{n-1}^{\lim }}t_{n-1}^{d}\text{=}\alpha $;$t_{1}^{d}+t_{2}^{d}+\cdots +t_{n-1}^{d}=\beta $;则式(12) 变为
| $\alpha +t_{n}^{d}=t_{n}^{lim}$ | (13) |
当
通过分析可知,动态偏差的持续时间限值介于偏差变化过程中最小持续时间限值和最大持续时间限值之间。
研究偏差持续时间限值
按照偏差持续时间限值
对每一层的偏差进行定义,表达不同的意义。第一层是正常工艺参数称为“正常值”
从正常值
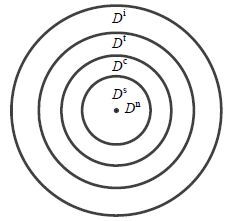
|
图 2 偏差“层级”模型 Fig.2 Schematic diagram of the “Hierarchy” model of deviation |
首先,建立过程系统的数学模型。根据P&ID图划分节点,分别建立每个节点的数学模型。其次,寻找每个节点内的“危险点”。危险点是偏差引起危险出现的标志。最后,寻找偏差的边界值,区分偏差所属的层级。
偏差的偏离程度从零开始增大,记录每个偏差引起危险点开始出现的时间,时间无限大的偏差是安全阈值
利用MATLAB编制智能化求解包,设计GUI用户界面,开发出建立偏差“层级”模型的软件。该智能化求解包选用Runge-Kutta算法中ode45函数建立系统的数学模型,设置事件events和具有合理步长的偏差循环,记录每个偏差数值及达到事件events的时间,达到事件events的时间即为持续时间限值
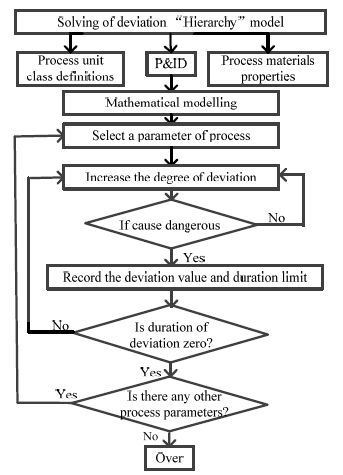
|
图 3 偏差“层级”模型求解流程 Fig.3 Solving process of the "Hierarchy" model |
将动态偏差
Woezik[20]研究了用含氮酸氧化2-辛醇生成2-辛酮的反应机理,并且建立了相应的数学模型。Eizenberg[21]对该数学模型进行了改进并利用MATLAB建立了模拟软件,对该反应实施了智能化HAZOP定量分析,结果如表 1所示。
| 表 1 引起“飞温”的部分偏差 Table 1 Deviations that may cause temperature runaway |
该反应中氧化2-辛醇生成2-辛酮是主反应,进一步氧化生成含碳酸是副反应,反应温度对主、副反应的影响巨大。当反应温度不超过273 K时,只有大约7.5% 的2-辛酮氧化成含碳酸;当反应温度超过278 K时,2-辛酮几乎全部氧化成含碳酸,并且系统出现“飞温”现象,会引起爆沸、爆炸等危险。因此,该体系反应温度278 K是出现“飞温”现象进而引起更危险后果的标志。在众多影响反应温度的因素中,本文选取冷却介质初温作为偏差“层级”模型研究的实例。
4.2 建立冷却介质初温偏差“层级”模型根据前述的建立偏差“层级”模型方法,将文献中的实例代入MATLAB智能化求解包,得到如下结果:初始状态下,冷却介质初温由260 K逐渐增大,记录每一个偏差值引起该体系反应温度达到或超过“最高温度限值”278 K时的持续时间。冷却介质初温在265 K以下,此间歇反应在操作时间72000 s内,不会发生危险;超过275.5 K后,此间歇反应会立即发生危险;在265~275.5 K时,持续时间在对应的7168~973 s,此间歇反应不会发生危险,持续时间超出后,会发生危险。
假设控制该体系冷却介质初温由纠错偏差
| 表 2 冷却介质初温偏差“层级”模型 Table 2 "Hierarchy" model for the initial temperature deviation of coolant |
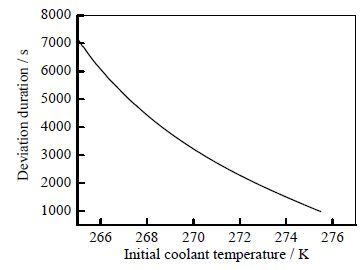
|
图 4 引发偏差Dt Fig.4 Triggered deviation Dt |
利用“动态偏差阶梯化求解”法,将冷却介质初温动态偏差
| 表 3 冷却介质初温动态偏差 Table 3 Dynamic deviation of the initial temperature of coolant |
| $t_{e}^{d}\text{ = }t_{n}^{\lim }\sum\limits_{i=1}^{n}{\frac{t_{i}^{d}}{t_{i}^{\lim }}}=1145\times \left( \frac{200}{1145}+\frac{400}{3218}+\frac{300}{7168}+\frac{600}{\infty } \right)s=390s,$ |
即该动态偏差的有效偏差为275 K (390 s),因390 s < 545 s,所以该动态偏差不会引起系统危险。
如
Eizenberg研究冷却介质初温的安全范围是260 ~ 265 K,超出265 K后该体系会出现“飞温”。由表 2可知,该体系冷却介质初温由265 K到275.5 K的偏差持续时间
本文以偏差持续时间是否达到限值作为是否引起系统危险的判断依据,明确了偏差引起系统危险的必要条件,将HAZOP与动态模拟相结合,建立基于偏差持续时间的“层级”模型,将偏差分为正常值
符号说明:
| Dn,Ds,Dc,Dt,Di | ——偏差“层级”模型的正常值,安全阈值, | | ——动态偏差不同数值的持续时间 |
| 纠错偏差,引发偏差,不可逆偏差 | tlim | ——偏差持续时间限值,又称为引发时间 | |
| R1 | —— | ——动态偏差用第n个数值表示时的持续时 | |
| R2 | —— | 间限值 | |
| R3 | —— | x | ——工艺参数 |
| t,t0 | ——系统时间,系统初始时间 | x1,x2,…,xn | ——按时间顺序排列的动态偏差不同数值 |
| tc | ——纠错时间 | ——动态偏差 | |
| ——动态偏差用第n个数值表示时的纠错时间 | ——用动态偏差第n个数值表示的有效偏差 | ||
| | ——偏差持续时间,以动态偏差某一数值表示时的有效持续时间 | y,y0 | ——系统输出变量,系统初始状态输出变量 |
| [1] | CUI Lin (崔琳). Research and integration of HAZOP automation methods for petrochemical processes (石油化工过程HAZOP专家系统与集成研究)[D]. Beijing (北京):Beijing University of Chemical Technology (北京化工大学), 2009. |
| [2] | Catino C A, Ungar L H. Model-based approach to automated hazard identification of chemical plants[J]. AICHE Journal , 1995, 41(41): 97-109. |
| [3] | Venkatasubramanian V, Vaidhyanathan R. A knowledge-based framework for automating HAZOP analysis[J]. AICHE Journal , 1994, 40(3): 496-505. DOI:10.1002/(ISSN)1547-5905. |
| [4] | Zhao C, Bhushan M, Venkatasubramanian V. PHA Suite:an automated HAZOP analysis tool for chemical processes:Part I:knowledge engineering framework[J]. Process Safety & Environmental Protection , 2005, 83(6): 509-532. |
| [5] | Zhao C, Bhushan M, Venkatasubramanian V. PHASuite:An automated HAZOP analysis tool for chemical processes:Part Ⅱ:implementation and case study[J]. Process Safety & Environmental Protection , 2005, 83(6): 533-548. |
| [6] | Wang F, Gao J, Wang H. A new intelligent assistant system for HAZOP analysis of complex process plant[J]. Journal of Loss Prevention in the Process Industries , 2012, 25(3): 636-642. DOI:10.1016/j.jlp.2012.02.001. |
| [7] | Khan F I, Abbasi S A. Towards automation of HAZOP with a new tool EXPERTOP[J]. Environmental Modelling & Software , 2000, 15(1): 67-77. |
| [8] | Srinivasan R, Dimitriadis V D, Shah N, et al. Integrating knowledge-based and mathematical programming approaches for process safety verification[J]. Computers & Chemical Engineering , 1997, 21(10): S905-S910. |
| [9] | Viswanathan S N S, Venkatasubramanian V. Hybrid framework for hazard identification and assessment in batch processes[J]. AICHE Journal , 2002, 48(8): 1765-1774. DOI:10.1002/(ISSN)1547-5905. |
| [10] | Abuswer M, Amyotte P, Khan F. A quantitative risk management framework for dust and hybrid mixture explosions[J]. Journal of Loss Prevention in the Process Industries , 2013, 26(2): 283-289. DOI:10.1016/j.jlp.2011.08.010. |
| [11] | Hoseyni S M, Pourgol-Mohammad M, Tehranifard A A, et al. A systematic framework for effective uncertainty assessment of severe accident calculations; hybrid qualitative and quantitative methodology[J]. Reliability Engineering & System Safety , 2014, 125(1): 22-35. |
| [12] | Huang H, Adjiman C S, Nilay S. Quantitative framework for reliable safety analysis[J]. AICHE Journal , 2002, 48(48): 78-96. |
| [13] | LIU Xiu-hong(刘旭红), ZHOU Le-ping(周乐平), ZHAO Dong-feng(赵东风), et al. Study on HAZOP quantitative analysis-combining HAZOP with simulation(HAZOP分析的量化研究-HAZOP分析与过程模拟相结合)[J]. Petrochemical Safety and Environmental Protection Technology(石油化工安全环保技术) , 2009, 25(2): 19-22. |
| [14] | Nan B M S, Syahril A, Suzuki K, et al. HAZOP analysis management system with dynamic visual model aid[J]. American Journal of Applied Sciences , 2010, 7(7): 943-948. DOI:10.3844/ajassp.2010.943.948. |
| [15] | Fu J M, Zhao D F, Zhang C, et al. Quantitative process risk analysis based on dynamic simulation of gas gathering process[J]. Advanced Materials Research , 2011, 399-401: 2226-2230. DOI:10.4028/www.scientific.net/AMR.399-401. |
| [16] | GUO Li-jie(郭丽杰), KANG Jian-xin(康建新). Quantitative HAZOP analysis approach based on dynamic process simulation(基于动态过程模拟的定量化HAZOP分析方法)[J]. Computers and Applied Chemistry(计算机与应用化学) , 2015, 32(4): 392-396. |
| [17] | Tian W, Du T, Mu S. HAZOP analysis-based dynamic simulation and its application in chemical processes[J]. Asia-Pacific Journal of Chemical Engineering , 2015, 10(6): 923-935. DOI:10.1002/apj.1929. |
| [18] | SHI Yan-juan(石艳娟), FU Jian-min(付建民), ZHENG Xiao-yun(郑晓云), et al. HAZOP and HYSYS based simulation and consequence quantization of technological parameter deviation(基于HYSYS和HAZOP的工艺参数偏差模拟与后果量化)[J]. China Safety Science Journal(中国安全科学学报) , 2015, 12(25): 75-80. |
| [19] | ZHAO Wen-fang(赵文芳), JIANG Chun-min(姜春明), JIANG Wei-wei(姜巍巍), et al. The core technology of HAZOP analysis(HAZOP分析核心技术)[J]. Safety Health & Environment(安全健康和环境) , 2005, 5(3): 1-3. |
| [20] | Woezik B A A V, Westerterp K R. Runaway behavior and thermally safe operation of multiple liquid-liquid reactions in the semi-batch reactor:the nitric acid oxidation of 2-octanol[J]. Chemical Engineering & Processing Process Intensification , 2002, 41(1): 59-77. |
| [21] | Eizenberg S, Shacham M, Brauner N. Combining HAZOP with dynamic simulation-applications for safety education[J]. Journal of Loss Prevention in the Process Industries , 2006, 19(6): 754-761. DOI:10.1016/j.jlp.2006.07.002. |




