2. 新能源系统工程与装备陕西省高校工程研究中心, 陕西 西安 710049;
3. 陕西省能源化工过程强化重点实验室, 陕西 西安 710049
2. Engineering Research Center of New Energy System Engineering and Equipment, University of Shaanxi Province, Xi′an 710049, China;
3. Shaanxi Key Laboratory of Energy Chemical Process Intensification, Xi′an 710049, China
锂离子电池的老化过程和剩余寿命预测对于电池应用的安全性具有重要意义。锂电池的老化过程可分为日历老化和循环老化[1-2]。日历老化是指电池在存储状态下发生老化,主要受电池荷电状态(SOC)和温度影响;循环老化则是指电池在循环充放电过程中的容量衰减。电池循环老化过程复杂,主要受温度、倍率和SOC等诸多因素影响。这些因素在电池内部相互耦合,所引起的固体电解质界面膜(SEI)增长和锂沉积等过程是电池老化的主要机制[3-4]。电池的循环老化可以分为2个阶段:第1阶段是负极SEI膜增长主导的线性衰退过程;第2阶段是锂沉积主导的非线性衰退过程[5]。
目前已有许多电池剩余寿命预测的方法,可分数据驱动方法、物理模型方法和混合方法等3类。基于数据驱动模型的预测方法是直接提取电池老化数据,不考虑电池的电化学过程,例如采用前馈神经网络(FFNN)[6]、支持向量回归(SVR)[7]、关联向量机(RVM)[8]、高斯过程回归(GPR)[9]、深度神经网络(DNN)和长短期记忆模型(LSTM)[10]等方法。与数据驱动的电池寿命预测方法相比,基于物理模型的预测方法考虑了电池的电化学和动力学特性以及电池工作状况和老化机理等影响,例如电化学模型(EM)、等效电路模型(ECM)和经验模型等[11]。经验模型具有形式和使用简单的特点,广泛应用于电池循环寿命的快速预测[12]。
对于基于SEI膜生长机制的电池循环寿命经验模型,其常见形式是循环数的1/2次方和双指数模型。Bloom等[13]的研究表明,锂离子电池的日历寿命和循环寿命遵循循环数的1/2次方和Arrhenius动力学。为了提高不同温度下电池寿命模型的外推能力,Wang等[14]建立了考虑温度关联Arrhenius动力学的电池老化模型,并关联了倍率与循环老化的指数依赖关系。Sui等[15]考虑时间、温度和SOC等因素影响,采用简单而准确的两步非线性回归方法建立电池老化模型。Stroe等[16]提出用于锂离子电池加速寿命测试的3阶段方法,考虑了加速老化阶段特性,建立了电池寿命预测模型,该模型可预测锂离子电池的容量衰退和功率下降。Sarasketa-Zabala等[17]比较了恒定与非恒定操作条件下电池循环老化行为,并定义用于电池容量衰减建模的最佳放电深度(DOD)范围,确定电池老化函数的形式。Chen等[18]提出一种经验-数据混合驱动模型的预测方法,即利用先验知识和历史数据集对锂离子电池在容量骤降情况下的寿命进行了预测。Cai等[2]提出可同时预测电池两阶段衰退的经验模型,以评估不同储存条件下电池的循环衰退。虽然前人针对基于电池电化学过程机理的经验模型开展了广泛研究,但是传统的经验模型很少考虑电池的非线性衰退阶段。
为了快速准确预测锂离子电池的循环寿命,并快速识别循环老化过程两阶段的转折点,本研究考虑SEI增长和锂沉积机制,建立了锂电池两阶段循环老化预测模型,通过两阶段电化学模型模拟计算获得不同条件下电池SEI增长和锂沉积所引起容量衰减的电池老化轨迹数据集,采用两步非线性回归方法建立了可快速精确预测电池单体循环老化过程的经验模型,并进行了验证和分析。
2 锂电池老化过程经验模型的建立根据容量衰退曲线的转折点(Knee点),锂离子电池的老化过程可分为2个阶段:在Knee点之前,电池的容量衰退曲线呈线性衰退,其主导机制是SEI膜生长;在Knee点之后,电池的容量衰退曲线为非线性衰退,其主导机制是锂沉积[5]。Knee点处的循环数由SEI增长和锂沉积在单位循环内引起老化的大小关系确定。因此,在2个阶段分别考虑SEI增长和锂沉积两种容量衰退主导机制时,电池在2个阶段的总容量衰退Qtotal可由SEI增长和锂沉积引起的容量衰退QSEI和QLi加和得到。本研究将分别建立SEI老化和锂沉积老化过程预测的2阶段老化半经验模型。
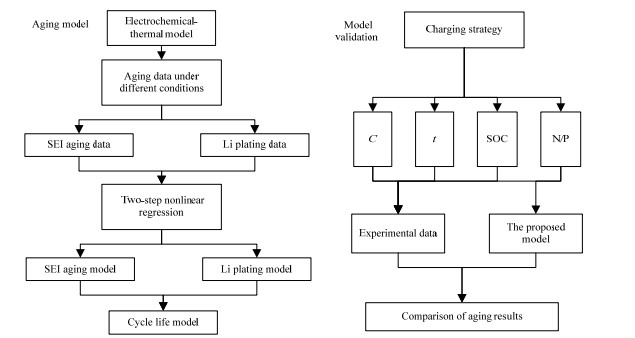
研究采用两步非线性回归方法分别拟合SEI和锂沉积引起的老化过程。第1步,建立计算条件下容量衰退对循环数的依赖关系;第2步,建立容量衰退对环境温度、充电倍率C、SOC区间、负极容量与正极容量比(N/P)的依赖关系。利用非线性最小二乘法对参数进行优化,使回归函数与模拟所得数据吻合。在获得SEI引起和锂沉积引起的老化过程计算模型后,对其加和可得到电池总的老化过程。此后,通过实验数据进行验证,并比较循环老化计算模型和传统经验模型的结果,电池总的循环老化过程及验证流程如图 1所示。本模型假设忽略各因素之间的相互影响。
|
图 1 电池两阶段老化经验模型的计算过程 Fig.1 Calculation flowchart of the two- stage aging model |
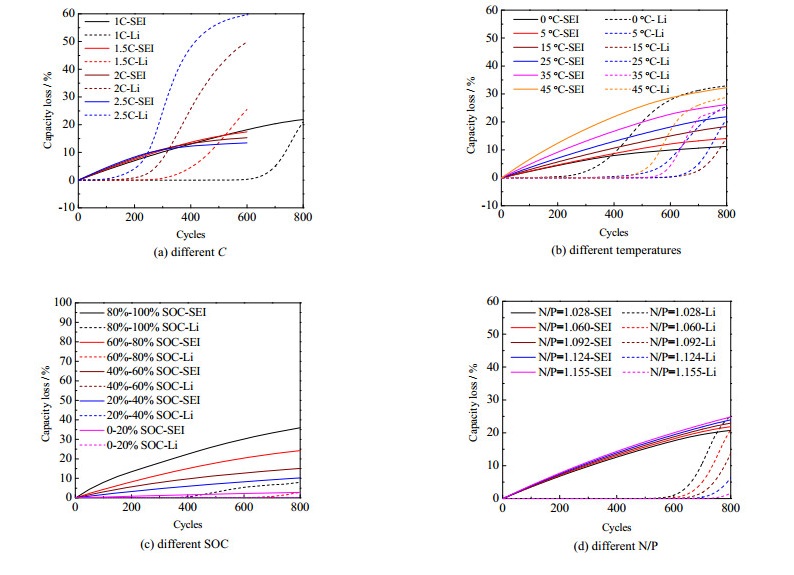
本研究采用文献[5]所建立的电化学-热耦合模型,对不同充放电条件下的2.05 A⋅h的镍钴锰酸锂(NCM)电池进行模拟,计算条件如表 1所示,得到本研究所用的数据集。电池充电采用不同的策略,电池放电采用1C恒流恒压(CC-CV)策略,模拟计算得到不同充电倍率(Case 1~Case 4) (1C~2.5C)、环境温度(Case 5~Case 9) (0~45 ℃)、充电SOC区间(Case 10~Case 17) (0~20%、20%~40%、40%~60%、60%~80%、80%~100%、10%~90%、25%~75%、45%~55%)和正负极电极容量比N/P (Case 18~Case 21) (1.028、1.092、1.124、1.155)等不同参数组合下的21组电池衰退数据作为循环老化模型拟合的数据集。图 2(a)、(b)、(c)和(d)分别给出了不同充电倍率、温度、SOC区间和N/P下的SEI和锂沉积引起的老化过程。
|
|
表 1 电池计算条件汇总 Table 1 Summary of different simulation conditions |
|
图 2 不同情况下,SEI和锂沉积引起老化随循环数的变化情况 Fig.2 Aging profiles due to SEI and lithium plating as a function of cycle numbers under different conditions |
为了确定老化数据对应最合适数学函数形式及其拟合参数,研究基于最小二乘拟合方法实施了多步优化过程。
电池老化过程建模可分为两步。
第1步:建立不同老化情况下电池容量衰减与循环次数的关系。通过对不同函数的比较和评价,选择最佳的拟合结果。以Case 1的老化数据为例,4种函数形式的拟合结果如表 2所示,表中a、b、c为拟合函数需要确定的参数;x、y为拟合函数的自变量和因变量。由表可知,指数函数类型的拟合结果整体效果最好,幂函数次之。结合相关文献的研究,本研究选择幂函数形式。为了使函数的整体误差较小且拟合参数少,选择带有固定常数项的幂函数作为电池老化的拟合函数。
|
|
表 2 不同拟合形式的容量衰退曲线相关系数R2及性能 Table 2 Correlation coefficients and performance of capacity decline curves under different fitting functions |
第2步:分别对不同温度、倍率、SOC和N/P比下的容量衰退特性进行拟合。温度对电池老化有着显著的影响,不同温度下SEI引起的老化如图 2(b)所示,考虑温度变化的容量衰退曲线的拟合系数如表 3所示,at和bt分别为拟合函数的系数。表中考虑温度影响时,SEI引起老化QSEI(n, t)随循环数的变化可以表示为
| $ {Q_{{\text{SEI}}}}(n, t) = {a_t}{n^{{b_t}}} - 0.6 $ | (1) |
| $ {a_t} = {\text{ 0}}{\text{.001 71}}{{e} ^{{\text{0}}{\text{.103 1}}t{\text{ }}}}{\text{ + 0}}{\text{.054 7}}{{e} ^{{\text{0}}{\text{.022 6}}t{\text{ }}}} $ | (2) |
| $ {b_t} = - {\text{7}}{\text{.367}} \times {\text{1}}{{\text{0}}^{ - {\text{6}}}} \times {t^{{\text{2}}{\text{.548}}}}{\text{ + 0}}{\text{.818 8}} $ | (3) |
|
|
表 3 不同温度下的老化曲线拟合系数 Table 3 Aging curve fitting coefficients at different temperatures |
式中:n为循环数;t为温度,℃。
图 2(a)给出了不同倍率下由SEI引起的电池老化,考虑倍率变化的容量衰退曲线的拟合系数如表 4所示,表中aC和bC分别为拟合函数的系数。类似的,考虑倍率影响时,SEI引起老化QSEI(n, C)随循环数的变化可以表示为
| $ {Q_{{\text{SEI}}}}(n, C) = {a_C} \cdot {n^{{b_C}}} - 0.6 $ | (4) |
| $ {a_C} = {\text{ 0}}{\text{.04}}{{e} ^{{\text{0}}{\text{.983 8}}C}} $ | (5) |
| $ {b_C} = - 0.030{\text{ }}6{C^{{\text{2}}{\text{.471 2}}}} + 0.833{\text{ }}8 $ | (6) |
|
|
表 4 不同倍率下的老化曲线拟合系数 Table 4 Aging curve fitting coefficients at different C-rates |
已有研究表明,平均SOC(
| $ {Q_{{\text{SEI}}}}(n, \overline {\rm{SOC}} , {\rm{DOD}}) = {a_{{\text{soc}}}} \cdot {n^{{b_{{\text{soc}}}}}} - 0.6 $ | (7) |
|
|
表 5 不同SOC区间的老化曲线拟合系数 Table 5 Aging curve fitting coefficients at different SOC ranges |
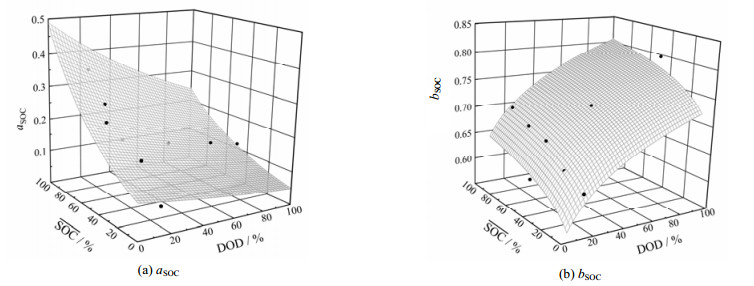
|
图 3 曲线拟合系数与平均SOC和DOD的关系 Fig.3 Relationship between curve fitting coefficients and average SOC and DOD bSOC |
式中:
| $ {a_{{\text{SOC}}}} = {\text{0}}{\text{.102 3ex}}{{\text{p}}_{}}{\text{(1}}{\text{.564}}\overline {{\text{SOC}}} {\text{ - 0}}{\text{.716 7DOD)}} $ | (8) |
| $ {b_{{\text{SOC}}}} = 0.407({\overline {\rm{SOC}} ^{{\text{0}}{\text{.107}}}} + {\rm{DO}}{{\rm{D}}^{{\text{0}}{\text{.228}}}}) $ | (9) |
图 2(d)给出了不同N/P下由SEI引起的电池老化,考虑N/P变化的SEI引起的容量衰退QSEI(n, N/P) 可表示为
| $ {Q_{{\text{SEI}}}}(n, {\text{N/P}}) = {a_{{\text{NP}}}} \cdot {n^{{b_{{\text{N/P}}}}}} - 0.6 $ | (10) |
| $ {a_{{\text{N/P}}}} = {\text{ 0}}{\text{.016 6}}{\exp _{}}({\text{1}}{\text{.814 6N/P) }} $ | (11) |
| $ {b_{{\text{N/P}}}} = - {\text{2}}{\text{.211 6}}{({\text{N/P)}}^{{\text{0}}{\text{.072 4}}}} - {\text{3}}{\text{.017 8}} $ | (12) |
式中:aN/P和bN/P分别为拟合函数的系数,具体值如表 6所示。
|
|
表 6 不同N/P下的老化曲线拟合系数 Table 6 Aging curve fitting coefficients under different N/P ratios |
以上得到了不同温度、倍率、SOC和N/P下SEI引起容量衰退的拟合结果。由于忽略了不同因素之间可能存在的相互作用,可以将不同函数结合起来形成一个新的函数,其结果见表 7。表 7中系数a1、b1、a2、b2分别为计算SEI和锂沉积引起老化的系数,为了减小组合不同因素形成新函数的误差,需对新函数系数进行修正。QSEI(n, t, C,
|
|
表 7 两阶段电池老化经验模型 Table 7 Two-stage empirical models for lithium ion battery aging |
表 8给出了不同情况下(Case 1~Case 21)衰退曲线的拟合系数,其中Case 10~Case 12没有给出是因为在限制的SOC区间中循环充放电没有锂沉积反应发生。
|
|
表 8 不同情况下的锂沉积引起老化曲线拟合系数 Table 8 Aging curve fitting coefficients induced by lithium plating at different conditions |
对于第2阶段的老化过程,可以采用类似于第1阶段老化的方法得到锂沉积机制引起老化过程,其拟合函数如表 7所示。在得到不同状况下的锂沉积预测公式后,再对SEI引起和锂沉积引起的老化进行加和,得到电池总的老化。
3.3 电池容量衰退曲线的转折点与循环寿命对于电池容量衰退曲线的Knee点,可根据式(13)确定
| $ \begin{array}{l} {Q_{{\text{SEI}}}}({n^{\text{*}}}) - {Q_{{\text{SEI}}}}({n^{\text{*}}} - 1) > {Q_{{\text{Li}}}}({n^{\text{*}}}) - {Q_{{\text{Li}}}}({n^{\text{*}}} - 1) \hfill \\ {Q_{{\text{SEI}}}}({n^{\text{*}}} + 1) - {Q_{{\text{SEI}}}}({n^{\text{*}}}) \leqslant {Q_{{\text{Li}}}}({n^{\text{*}}} + 1) - {Q_{{\text{Li}}}}({n^{\text{*}}}) \hfill\end{array} $ | (13) |
式中:QSEI(n*)和QLi(n*)分别表示循环数为n*时的SEI和锂沉积引起的老化,满足上述不等式的n*值即为该情况下的Knee点的循环数。此时,可以根据操作条件和上述模型来预测电池的Knee点和循环寿命。
4 两阶段老化过程经验模型验证为了验证所建立模型的有效性,将文献所建立的经验模型和实验结果进行比较。
本研究采用2.05 A⋅h的Sanyo UR18650E NCM电池,与使用相同电池的文献的实验数据进行比较。选择了2种对比模型:模型1是式(14)表示的考虑温度影响的老化预测半经验模型[21],模型2是式(15)表示的考虑温度和80% 剩余容量为转折点的老化预测半经验模型[22]。
| $ {Q_{{\text{emp1}}}} = B \cdot {\exp _{}}( - \frac{{{E_{\text{a}}}}}{{R \times t}}) \cdot A{h^z} $ | (14) |
式中:Qemp1表示由模型1所求电池老化,B和z为拟合系数和指数,Ea表示电池活化能,R表示气体常数,Ah表示电池的吞吐量。
| $ {Q_{{\text{emp2}}}} = {\exp _{}}{\text{(}}A \times t{\text{ + }}H{\text{)}} \cdot {n^J} + {\exp _{}}{\text{(}}D \times t{\text{ + }}E{\text{)}} \cdot {n^{F \times t{\text{ + }}G}} $ | (15) |
式中:Qemp2表示由模型2所求电池老化,A、D、E、F、G、H、和J均为拟合系数或指数。
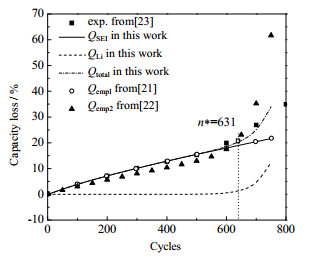
为了准确对比模型的效果,根据本研究的数据,对2个对比模型的系数取值进行修正,对模型变量进行等效转换。本研究容量衰退模型与实验结果的对比如图 4所示,其中0~100% SOC实验数据来自文献[23],QSEI、QLi和Qtotal由作者建立模型求得,Knee点循环数由不等式(13)求得,而Qemp1和Qemp2则是使用式(14)和式(15)求得。
|
图 4 25 ℃下,模型模拟结果与实验结果比较 Fig.4 Comparison of modeling and experimental results at 25 ℃ |
由图 4可知,SEI引起老化QSEI与半经验模型的老化Qemp1和实验数据在Knee点之前基本重合,此时电池衰退主要由SEI生长控制,属于第1阶段老化。而Knee点之后的第2阶段加速老化,相比于模型1,本研究所提的模型更接近于实际电池老化数据,此时锂沉积是电池老化的主要原因。Qemp2在两阶段的容量衰减曲线与实验数据变化趋势相似,但与实验数据的差距大于本研究所提模型的模拟结果。因此,比较3种模型的模拟效果,可以得出本研究所提模型 > 模型2 > 模型1。
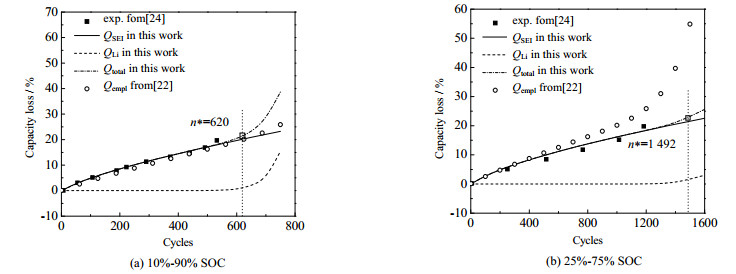
根据文献[24]的实验数据,对不同SOC区间下的结果进行比较,并与模型2和本研究所提模型模拟结果比较,结果如图 5所示。由图 5可知,本模型相比于模型2,预测效果更好,说明本研究所提模型更可以适应不同SOC区间的老化预测。此外,10%~90% SOC相对于25%~75% SOC,拟合效果较好,其可能的原因是电化学模型中所考虑的电池老化机理未考虑各影响因素之间耦合关系。
|
图 5 35 ℃下,不同SOC区间下的模型与实验结果对比 Fig.5 Comparison of modeling and experimental results under different SOC ranges at 35 ℃ |
关于锂离子电池老化经验模型的研究,主要考虑SEI生长主导的线性老化,很少关注锂沉积主导的加速老化。本研究考虑两种老化机制,构建并验证了预测两阶段老化过程和转折点的经验模型。
结果表明,研究所建立的经验模型,可以快速准确预测不同参数条件下电池的两阶段老化过程,可以定量确定不同情况下的两阶段转折点。后续研究可以结合数据驱动模型改进本文所提经验模型,得到更加精确和高效的经验模型,应用于电池快充策略的设计和优化。
| [1] |
REDONDO-IGLESIAS E, VENET P, PELISSIER S. Modelling lithium-ion battery ageing in electric vehicle applications—Calendar and cycling ageing combination effects[J]. Batteries, 2020, 6(1): 14. DOI:10.3390/batteries6010014 |
| [2] |
CAI W F, CHEN K C. Influence of the calendar aging on the cycle aging of LiNiMnCoO2 lithium-ion batteries[J]. Journal of the Electrochemical Society, 2021, 168(12): 120525. DOI:10.1149/1945-7111/ac405a |
| [3] |
YANG X G, LENG Y J, ZHANG G S, et al. Modeling of lithium plating induced aging of lithium-ion batteries: Transition from linear to nonlinear aging[J]. Journal of Power Sources, 2017, 360: 28-40. DOI:10.1016/j.jpowsour.2017.05.110 |
| [4] |
SCHUSTER S F, BACH T, FLEDER E, et al. Nonlinear aging characteristics of lithium-ion cells under different operational conditions[J]. Journal of Energy Storage, 2015, 1: 44-53. DOI:10.1016/j.est.2015.05.003 |
| [5] |
LYU H C, HUANG X K, KANG L X, et al. Quantitative estimation of turning point of ageing based on a two-stage model for lithium-Ion batteries[J]. Journal of the Electrochemical Society, 2022, 169(1): 010533. DOI:10.1149/1945-7111/ac4b1b |
| [6] |
WU J, ZHANG C B, CHEN Z H. An online method for lithium-ion battery remaining useful life estimation using importance sampling and neural networks[J]. Applied Energy, 2016, 173: 134-140. DOI:10.1016/j.apenergy.2016.04.057 |
| [7] |
ZHAO Q, QIN X L, ZHAO H B, et al. A novel prediction method based on the support vector regression for the remaining useful life of lithium-ion batteries[J]. Microelectronics Reliability, 2018, 85: 99-108. DOI:10.1016/j.microrel.2018.04.007 |
| [8] |
LIU D T, ZHOU J B, PAN D W, et al. Lithium-ion battery remaining useful life estimation with an optimized relevance vector machine algorithm with incremental learning[J]. Measurement, 2015, 63: 143-151. DOI:10.1016/j.measurement.2014.11.031 |
| [9] |
LI L L, WANG P C, CHAO K H, et al. Remaining useful life prediction for lithium-Ion batteries based on gaussian processes mixture[J]. Plos One, 2016, 11(9): e0163004. DOI:10.1371/journal.pone.0163004 |
| [10] |
QIAO J S, LIU X F, CHEN Z H. Prediction of the remaining useful life of lithium-ion batteries based on empirical mode decomposition and deep neural networks[J]. IEEE Access, 2020, 8: 42760-42767. DOI:10.1109/ACCESS.2020.2977429 |
| [11] |
LI W H, SENGUPTA N, DECHENT P, et al. One-shot battery degradation trajectory prediction with deep learning[J]. Journal of Power Sources, 2021, 506: 230024. DOI:10.1016/j.jpowsour.2021.230024 |
| [12] |
SULZER V, MOHTAT P, AITIO A, et al. The challenge and opportunity of battery lifetime prediction from field data[J]. Joule, 2021, 5(8): 1934-1955. DOI:10.1016/j.joule.2021.06.005 |
| [13] |
BLOOM I, COLE B W, SOHN J J, et al. An accelerated calendar and cycle life study of Li-ion cells[J]. Journal of Power Sources, 2001, 101(2): 238-247. DOI:10.1016/S0378-7753(01)00783-2 |
| [14] |
WANG J, PUREWAL J, LIU P, et al. Degradation of lithium ion batteries employing graphite negatives and nickel–cobalt–manganese oxide+spinel manganese oxide positives: Part 1, Aging mechanisms and life estimation[J]. Journal of Power Sources, 2014, 269: 937-948. DOI:10.1016/j.jpowsour.2014.07.030 |
| [15] |
SUI X, ŚWIERCZYŃSKI M, TEODORESCU R, et al. The degradation behavior of LiFePO4/C batteries during long-term calendar aging[J]. Energies, 2021, 14(6): 1732. DOI:10.3390/en14061732 |
| [16] |
STROE D I, ŚWIERCZYŃSKI M, STAN A I, et al. Accelerated lifetime testing methodology for lifetime estimation of lithium-ion batteries used in augmented wind power plants[J]. IEEE Transactions on Industry Applications, 2014, 50(6): 4006-4017. DOI:10.1109/TIA.2014.2321028 |
| [17] |
SARASKETA-ZABALA E, GANDIAGA I, MARTINEZ-LASERNA E, et al. Cycle ageing analysis of a LiFePO4/graphite cell with dynamic model validations: Towards realistic lifetime predictions[J]. Journal of Power Sources, 2015, 275: 573-587. DOI:10.1016/j.jpowsour.2014.10.153 |
| [18] |
CHEN D, MENG J H, HUANG H Y, et al. An empirical-data hybrid driven approach for remaining useful life prediction of lithium-ion batteries considering capacity diving[J]. Energy, 2022, 245: 123222. |
| [19] |
SCHMALSTIEG J, KäBITZ S, ECKER M, et al. A holistic aging model for Li(NiMnCo)O2 based 18650 lithium-ion batteries[J]. Journal of Power Sources, 2014, 257: 325-334. |
| [20] |
DE HOOG J, TIMMERMANS J M, IOAN-STROE D, et al. Combined cycling and calendar capacity fade modeling of a nickel-manganese-cobalt oxide cell with real-life profile validation[J]. Applied Energy, 2017, 200: 47-61. DOI:10.1016/j.apenergy.2017.05.018 |
| [21] |
LEE Y J, CHOI H Y, HA C W, et al. Cycle life modeling and the capacity fading mechanisms in a graphite /LiNi0.6Co0.2Mn0.2O2 cell[J]. Journal of Applied Electrochemistry, 2015, 45(5): 419-426. DOI:10.1007/s10800-015-0811-6 |
| [22] |
DIAO W P, SAXENA S, PECHT M. Accelerated cycle life testing and capacity degradation modeling of LiCoO2-graphite cells[J]. Journal of Power Sources, 2019, 435: 226830. |
| [23] |
KEIL J, JOSSEN A. Electrochemical modeling of linear and nonlinear aging of lithium-ion cells[J]. Journal of the Electrochemical Society, 2020, 167(11): 110535. |
| [24] |
ECKER M, NIETO N, KäBITZ S, et al. Calendar and cycle life study of Li(NiMnCo)O2-based 18650 lithium-ion batteries[J]. Journal of Power Sources, 2014, 248: 839-851. |




