随着21世纪环境恶化以及能源枯竭等一系列问题的出现,化学工业正面临着前所未有的机遇和挑战。微通道所具有的良好的传热传质性能及高度集成性[1, 2],使其在化工领域有着广泛的应用。其中微反应器表现出的诸多优点引起了国内外学者的广泛关注[3],科学界致力于探索新的反应途径使化工生产更加经济和环保。流型作为影响两相流压力损失和流动参数的重要影响因素,对其进行研究就显得尤为重要。然而,由于微通道内两相流流型分布受到惯性力、通道几何形状和尺寸、壁面润湿性及流体物性等因素的影响[4~8],传统的流型转换模型如Taitel-Dukler[9]模型及Mandhane[10]模型已不能预测微通道内气液两相流型转换界限。
Serizawa[11]等通过对不同直径微通道内气液两相流进行可视化实验研究,发现了几种不同寻常的流型,并验证了表面张力对于流型的影响远大于重力;Kawaji[12, 13]等通过对同样当量直径不同截面形状的微通道进行研究,得出不同截面微通道内相同流型间转换界限不同的结论;黏度和表面张力对流型的影响,也有相关学者进行了实验研究,得出一些规律[14]。然而,由于蛇形微通道结构的复杂性,现有文献中对其进行的相关报道依旧匮乏。
本文在理论分析并充分利用实验数据的基础上,通过详细的数值计算来考察90度Y型汇流下蛇形微通道内气液两相流流型间转换界限及影响因素。希望通过本文的研究,对蛇形微通道内气液两相流动有更深的了解,并为今后蛇形装置的设计奠定一定的理论基础。
2 数值方法 2.1 控制方程本文采用CLSVOF方法及Level Set和VOF耦合的方法对气液两相界面进行追踪,此方法综合了VOF和Level Set的高守恒性及界面光滑性的优点。其控制方程如下:
流动控制方程如下:
连续性方程
| $\frac{\partial \rho }{\partial \tau }+\nabla \rho \vec{u}~=0$ | (1) |
动量方程
| $\frac{\partial \left( \rho \vec{u} \right)}{\partial \tau }+\nabla \left( \rho \vec{u}\vec{u} \right)=-\nabla p+\nabla \mu \centerdot \left[ \nabla \vec{u}+{{\left( \nabla \vec{u} \right)}^{T}} \right]+\rho \vec{g}+\overrightarrow{{{F}_{\sigma }}}$ | (2) |
式中,r 为流体密度,$\vec{u}$为流体速度,t 为时间,p为压力,m 为动力黏度系数,$\vec{g}$为重力加速度。
表面张力模型采用Brackbill等[15]提出的连续表面张力模型(CSF)。
| ${{F}_{\sigma }}=\sigma k\left( \varphi \right)\nabla \left( \varphi \right)$ | (3) |
| $k\left( \varphi \right)=\nabla \centerdot \frac{\nabla \varphi }{\left| \nabla \varphi \right|}$ | (4) |
| $\delta \left( \varphi \right)=\left\{ \begin{matrix} 0{{,}_{{}}}\left| \varphi \right|\ge a \\ \frac{1}{2a}\left( 1+\cos \cos \frac{\pi \varphi }{a} \right){{,}_{{}}}\left| \varphi \right|<a \\ \end{matrix} \right.$ | (5) |
两相混合物的密度和黏度分别为:
| $\rho \left( \varphi \right)={{\rho }_{G}}+\left( {{\rho }_{L}}-{{\rho }_{G}} \right)H\left( \varphi \right)$ | (6) |
| $\mu \left( \varphi \right)={{\mu }_{G}}+\left( {{\mu }_{L}}-{{\mu }_{G}} \right)H\left( \varphi \right)$ | (7) |
| $H\left( \varphi \right)=\left\{ \begin{matrix} 0,\text{ }\varphi <-a \\ \frac{1}{2}[1+\frac{\varphi }{a}+\sin ([1+\frac{\varphi }{a}+\sin (\frac{\pi \varphi }{a})] \\ 1,\text{ }\varphi >a \\ \end{matrix} \right.{{,}_{{}}}\left| \varphi \right|\le a$ | (8) |
式中,G和L分别代表气相和液相,σ为表面张力,$~k\left( \varphi \right)$为界面曲率,a为界面厚度,$H\left( \varphi \right)$为Heaviside(阶跃)函数。
Level Set 方程
| $\frac{\partial \varphi }{\partial \tau }+\vec{u}\centerdot \nabla \varphi =0$ | (9) |
| $\varphi \left( \vec{x},\text{ }\!\!\tau\!\!\text{ } \right)=\left\{ \begin{matrix} d{{x}_{{}}}在液相中 \\ 0{{x}_{{}}}在界面处 \\ -d{{x}_{{}}}在气相中 \\ \end{matrix} \right.$ | (10) |
式中,φ为距离函数,$x$为位置矢量,d为τ时刻点到界面的最短距离。
VOF流体体积函数方程
| $\frac{\partial {{\alpha }_{G}}}{\partial \tau }+\vec{u}\centerdot \nabla {{\alpha }_{G}}=0$ | (11) |
| $\frac{\partial {{\alpha }}}{\partial \tau }+\vec{u}\centerdot \nabla {{\alpha }}=0$ | (12) |
式中,${{\alpha }_{G}}$为气相体积分数,${{\alpha }_{L}}$为液相体积分数。
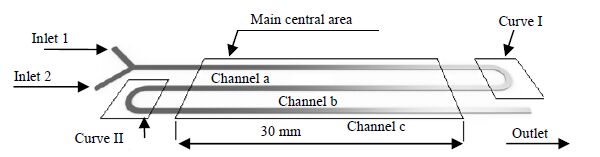
2.2 物理模型计算选用的物理模型如图 1所示。通道布置方式为立式蛇形微通道,弯道Ⅰ、Ⅱ及三条水平段构成一个蛇形单元,通道截面为矩形(800 μm×100 μm),Y型混合器夹角θ = 90°,进口段长度为10 mm,上、中、下水平段有效长度为50 mm,回转弯道1为半圆形结构,其内径为3 mm。气液两相分别从进口1、2流入。
|
图 1 蛇形微通道 Fig.1 Schematic diagram of the serpentine micro-channel |
表 1给出了气液两相在模拟过程中所使用的物性参数值。计算域采用时间非稳态计算,基于以下假设建立流动模型:1)假定入口处各相的体积分数均匀分布,2)微通道内重力影响不再显著,通道方向不加设定。3)流体物理性质为常数。在满足收敛的条件下,为提高精度,模拟过程中选用压力隐式算子分割算法(PISO)将压力-速度进行耦合,用压力插值算法(PRESTO)以及二阶迎风格式(second-order up-wind)进行计算,同时使用几何重构方案(Geo-Reconstruct)处理界面附近的插值。每次模拟过程中,为保证收敛,需要适当地调整时间步长和松弛因子。
| 表 1 模拟过程中气液两相的物性参数(20℃, 101.325 kPa) Table 1 Physical properties of gas and liquid phases used in simulation(20℃, 101.325 kPa) |
设置边界条件时,采用速度入口(velocity inlet)控制,分别设定气液两相入口速度,出口设置为自由出口(outflow),通道壁的设置为无滑移、无穿透的静止壁面,微通道内部液体可视为不可压缩非定常流动。同时,根据实验所选用的PDMS材料,依据文献[16],作者将气相、液相和壁面三相交界处形成的接触角设为110°。
2.4 网格独立性使用PRO.E进行几何造型,利用ICEM进行网格划分,对微通道壁面附近的网格进行边界层细化处理,然后将网格导入ANSYS FLUENT15.0 进行计算。计算之前取网格进行无关性验证,取5万~30万个,测定结果及计算速度。研究中发现逐渐细化网格,当网格数为20万左右时,计算结果不再随网格数的增加而改变,说明此时的网格划分达到计算精度的要求,花费时间最少,因此采用正六面体网格数为20万的网格划分保证计算精度的最大控制体积。
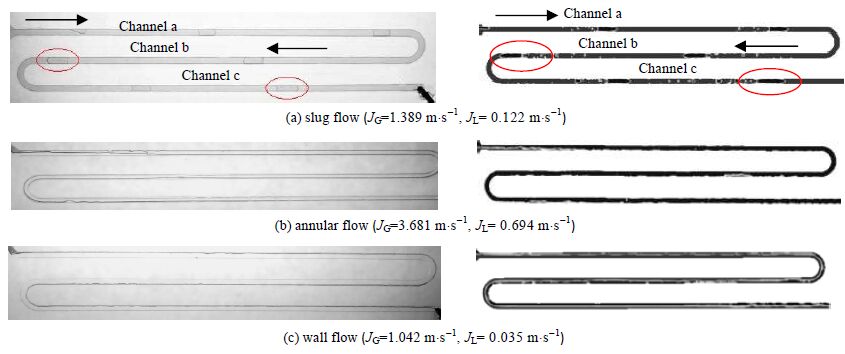
2.5 数值方法验证为验证数值方法的可靠性,本文通过可视化实验中的操作工况及实验结果对数值方法进行验证。实验测试段为蛇形微通道中心主体区域,其长度为30 mm,空气速度JG = 0.01~10 m⋅s-1,水速度 JL= 0.1~10 m⋅s-1,常温常压下进行。由图 2和图 3可以看到数值模拟与实验得出的流型特征基本一致,说明该方法能很好的模拟气液两相流在蛇形微通道内的流动情况。
|
图 2 实验结果 Fig.2 Experimental pictures of the flow processes |

|
图 3 模拟结果(气液两相体积分数分布) Fig.3 Simulation results of the flow process (gas-liquid two-phase volume fractions) |
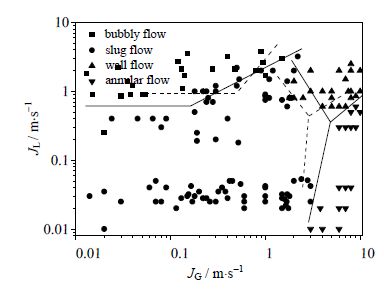
为定量验证,根据大量实验和模拟计算数据,绘制出了如图 4所示的流型图。如图 4所示,实线和虚线分别为根据实验数据和模拟数据绘制的流型图。显然,实验和模拟得出的流型过渡线基本一致,因此,本文所选取的求解算法可以正确反映蛇形微通道内气液两相流的实际情况。
|
图 4 实验与模拟流型图比较 Fig.4 Comparison of flow maps between experimental and simulation results |
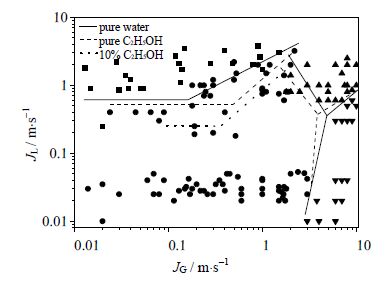
气液两相界面由于物性参数的突然改变,会受到表面张力的影响。流型是否会受到影响在数量上的判断主要取决于两个无量纲数:雷诺数Re和毛细数Ca或雷诺数Re和韦伯数We。当$Re\ll 1$时,若$Ca\gg 1$;或当$Re\gg 1$时,$We\ll 1$,则可忽略表面张力的影响。本文所采用的物理模型尺寸较小,不能忽略表面张力的影响。表面张力对流型的影响,已有相关学者进行了研究报道。其中,Zhang[17]通过对Y型通道进行实验研究发现表面张力降低时,Taylor流区域减小,泡状流及环状流区域向弹状流区域扩张;Pohoreki和Waelchili[18]也对泡状流与Taylor流的转换界限进行了研究,却得出截然相反的结论。为此,本文主要针对矩形截面蛇形微通道内泡状流与弹状流的转换界限进行分析。对液相分别采取了水、乙醇溶液和质量分数为10%的乙醇溶液,气相为空气的三组工质进行模拟计算。从表 1可以看出,随着不同溶液表面张力的逐渐缩小,液相流体黏度变化非常小,可以近似看成恒定的,因此可以通过这三组液相流体来衡量表面张力对流型转换界限的影响。流型图如图 5所示。
|
图 5 不同表面张力下流型转换的差异 Fig.5 Differences of flow pattern transition under different surface tensions (σ = 0.072 N⋅m-1 for water, σ = 0.0473 N⋅m-1 for pure C2H5OH, σ = 0.0225 N⋅m-1 for 10% C2H5OH) |
由图 5可以观察到,随着表面张力的降低,弹状流区域减小,泡状流向弹状流转换发生在更高的气相流速,更低的液相流速下。对此,作者可以进行了如下分析。
气液两相流中,泡状流的形成主要受表面张力的控制[17]。在Y型汇流处,气相顶端被挤压进液相,在气液相交界面处由剪切力夹断,因表面张力的作用形成球状。气泡的半径r与气液相压差有关,可由Young-Laplace公式解释:
| ${{P}_{G}}-{{P}_{L}}=\frac{2\text{ }\!\!\sigma\!\!\text{ }}{r}$ | (13) |
由于r<Dh,因此形成泡状流需要较大的压差。表面张力是唯一防止已有气泡扩大和破裂的力。随着表面张力的降低,气相惯性力增大,从泡状流转变成弹状流所需的液相紊流应力变小,即发生在更小的液相速度下。
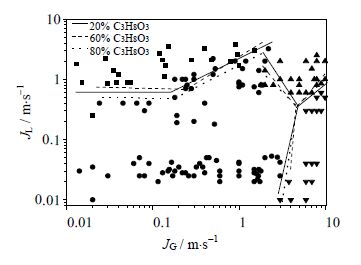
3.2 黏度对两相流型的影响本文选取了与已有实验不同的液相流体,研究了黏度对流型产生的影响。根据本文所建立的几何模型和所选取的算法,对液相采用质量分数分别为20%,60%和80%的丙三醇溶液,气相为空气的三组气-液相流体进行模拟。由表 1可以看出,随着丙三醇溶液质量分数的不断增加,表面张力的变化非常小,可以近似认为是恒定的,但运动黏度却不断增大,因此可以通过这三组不同的液相流体衡量黏度对流型转换界限的影响。流型图如图 6所示。
|
图 6 不同黏度下流型转换的差异 Fig.6 Differences of flow pattern transition under different liquid viscosities (μ = 0.001550 kg⋅(m⋅s)-1 for 20% glycerol, μ = 0.008823 kg⋅(m⋅s)-1 for 60% glycerol, μ = 0.045860 kg⋅(m⋅s)-1 for 80% glycerol) |
如图 6所示,随着黏度的增加,泡状流与弹状流的转换界限没有太大变化,弹状流向环状流过渡的界限稍向更高的气相流速移动,大体来看,黏度对气液两相流型的转换界限没有太大影响。这与Zhang[15]得出的结论一致。分析如下:
由Xiong和Chung[19]得出的结论可知,表面张力影响泡状流的形成,惯性力影响环状流的形成,而弹状流等流型的形成由二者共同作用影响。而惯性力,与液相黏度无关,故黏度对不同流型间的转换界限影响不大。
3.3 接触角对两相流型的影响剪切应力是流型转换的重要因素,很多学者[20]对不同接触角的通道壁面进行研究发现,当接触角为30°时,在JL0.01 m⋅s-1,5JG10 m⋅s-1的区域有波状流出现,而在其他接触角的壁面工况下则没有;Choi[21]也指出由于壁面的疏水性即接触角大于90度时,形成的弹状流头部和尾部呈半圆形,且气相与壁面之间没有明显液膜存在。因此,可以看出,通道壁面的性质对气液两相流有着显著影响。本文通过改变接触角来探究其对流型的影响,结论如下。
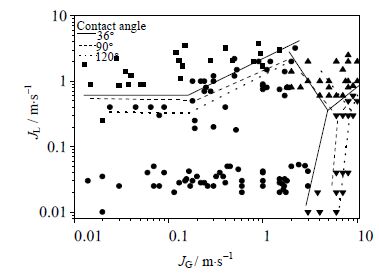
由图 7可以观察到,接触角增大时,弹状流区域扩张即泡状流与弹状流的转换界限发生在更高的液相速度条件下,同时,弹状流与环状流的转换界限发生在更低的气相速度下。总体来看,弹状流区域增大。产生这种现象有两方面原因:
|
图 7 不同壁面接触角下流型转换的差异 Fig.7 Differences of flow pattern transition under different wall contact angles |
一方面,对于疏水壁面,气泡更易于吸附在壁面上,气液两相交界面所占比例更大,摩擦因子减小,气液两相界面流动阻力小于水与壁面之间的流动阻力,因此通道中总的流动阻力与剪切应力与普通壁面相比更小,能量耗散也更小,导致流型转换更难。
另一方面,Ning等[22]提出的公式可以分析得出,
| $\Delta P={{P}_{L}}-{{P}_{G}}=\frac{4\text{ }\!\!\sigma\!\!\text{ coscos(}\pi \text{-}\Phi \text{)}}{W}$ | (14) |
式中,$\Phi $为壁面粗糙元与两相接触面积之间的夹角,w为粗糙元靠近壁面一侧的宽度。随接触角的增大,通道中压降增大;同时,由于壁面的疏水性,导致液塞在干燥壁面上流动造成较大能量损失,也会使得疏水壁面压降大于亲水壁面。从而使得泡状流向弹状流的转换界限发生在更高的液相速度条件下。与此同时,疏水壁面与亲水壁面相比,液相对气相的挤压力较小,不容易将气相剪断,故更易形成环状流。
3.4 截面形状对两相流型的影响 3.4.1 方形截面和矩形截面微通道流型间转换对比Thomas和Ho[23]曾通过实验对Dh = 150 mm (Dh为当量直径)的方形截面蛇形微通道内气液两相流进行研究,并绘制了流型图。为研究截面形状对流型的影响,本文将模拟结果与方形截面蛇形微通道流型图进行对比,结果如图 8所示。

|
图 8 截面高宽比对流型转换的影响 Fig.8 Effects of cross-section aspect ratios on flow pattern transition |
如图 8,与矩形截面微通道相比,方形截面微通道泡状流区域扩张,即更易形成泡状流,而弹状流向环状流转换则需要更高的液相速度和气相速度。马璨[24]对相同截面不同高宽比的微通道进行实验,发现当高宽比r=1时,相同流量下流速最大。
| $\Delta P=\frac{f\times \rho vL}{2{{D}_{h}}}$ | (15) |
式中,f是摩擦系数,L是微通道长度。由公式可知,流速达到最大时压降也达到最大。从泡状流的形成原因可分析出:压降增大,使得气泡半径减小,同时壁面剪切应力增大,使得微通道内更易形成泡状流,而弹状流向环状流转换则需要更高的气液相流速。
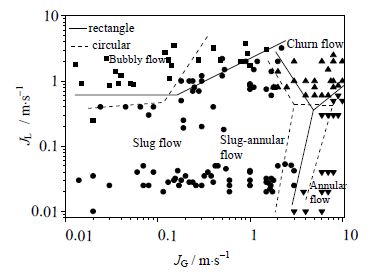
3.4.2 圆形截面和矩形截面微通道流型间转换对比Zhao[25]等曾对竖直放置矩形微通道进行实验研究并与圆形截面微通道气液两相流流型进行对比,发现角区的存在对流型有着显著影响。本文为研究截面形状的影响,将计算结果与Saisorn[26]等在Dh=150 mm的圆形截面微通道内进行实验所绘制出的气液两相流型图进行对比,结果如图 9所示。
|
图 9 圆形截面和矩形截面流型图对比 Fig.9 Comparison of flow patterns of circular and rectangular cross-sections |
显然,与圆形截面微通道相比,矩形截面微通道内气液两相流中环状流区域更大,泡状流向弹状流转换发生在更高的气相流速下。对此分析如下:
矩形截面通道中心到各壁面径向距离不等,而近壁面处表面张力较大,导致两相流动在近壁面处受壁面影响较大,从而使得流动存在一定的速度梯度。同时,角区聚集液体的能力更利于气泡的聚合,相分布和速度分布变化也更加剧烈,使得矩形截面微通道内流型转换较为容易。与矩形截面微通道相比,圆形截面微通道壁面距离中心位置相等,气泡四周液膜厚度一致,流动稳定,因而转变为环状流需更大的气相流速。
4 结 论(1) 弹状流区域随着表面张力的增加而变小,泡状流向弹状流转换发生在更高的气相流速,更低的液相流速下。即表面张力对弹状流影响较大。
(2) 本文通过对不同黏度液相流体进行模拟计算,发现黏度的改变对蛇形微通道内气液两相流流型间的转换界限影响很小。
(3) 当接触角增大时,微通道内弹状流区域扩张即泡状流与弹状流的转换界限发生在更高的液相速度条件下,同时,弹状流与环状流的转换界限发生在更低的气相速度下。
(4) 对于当量直径相同而截面形状不同的微通道,气液两相流型转换边界存在差异,说明截面形状影响两相流流动。
| [1] | Klaus J, Volker H, Holger l . Chemistry in microstructured reactors[J]. Angewandte Chemime International Edition , 2004, 43 (4) : 406-446 DOI:10.1002/(ISSN)1521-3773 |
| [2] | CHEN Guang-wen (陈光文), YUAN Quan (袁权). Micro-chemical technology[J]. Journal of Chemical Industry and Engineering, 2003, 54(4):427-439. |
| [3] | Dang Minhui, Yue Jun, Chen Guangwen . Numerical simulation of Taylor bubble formation in a microchannel with a converging mixing junction[J]. Chemical Engineering Journal , 2015, 262 : 616-627 DOI:10.1016/j.cej.2014.10.017 |
| [4] | Chung P M Y, Kawaji M . The effect of channel diameter on adiabatic two-phase flow characteristics in microchanels[J]. International Journal of Multiphase Flow , 2004, 30 (7-8) : 735-761 DOI:10.1016/j.ijmultiphaseflow.2004.05.002 |
| [5] | Yue J, Luo Linhai, Gonthieret Y . An experimental investigation of gas-liquid two-phase flow in single microchannel contactors[J]. Chemical Engineering Science , 2008, 63 (16) : 4189-4202 DOI:10.1016/j.ces.2008.05.032 |
| [6] | Pohorecki R, Sobieszuk P, Kula K . Hydrodynamic regimes of gas-liquid flow in a microreactor channel[J]. Chemical Engineering Science , 2008, 135 : 185-190 DOI:10.1016/j.cej.2007.02.024 |
| [7] | Rebrov E V . Two-phase flow regimes in microchannels[J]. Theoretical Foundations of Chemical Engineering , 2010, 44 (4) : 355-367 DOI:10.1134/S0040579510040019 |
| [8] | Shao N, Gavriilidis , Angeli P . Flow regimes for adiabatic gas-liquid flow in microchannels[J]. Chemical Engineering Science , 2009, 64 (11) : 2749-2761 DOI:10.1016/j.ces.2009.01.067 |
| [9] | Taitel Y, Dukler A E . Model for predicting flow regime transitions in horizontal and near horizontal gas-liquid flow[J]. AIChE Journal , 1976, 22 : 47-55 DOI:10.1002/(ISSN)1547-5905 |
| [10] | Mandhane J M, Gregory P M, Aziz K . A flow pattern map for gas-liquid flow in horizontal pipes[J]. International Journal of Multiphase Flow , 1974, 1 (4) : 537-553 DOI:10.1016/0301-9322(74)90006-8 |
| [11] | Serizawa A, Feng Z P, Kawara Z . Two-phase flow in microchannel[J]. Experimental Thermal and Fluid Science , 2002, 26 : 703-714 DOI:10.1016/S0894-1777(02)00175-9 |
| [12] | Kawhara A, Chung P M, Kawaji M . Investigation of two-phase flow pattern, void fraction, and pressure drop in a microchanel[J]. International Journal Multiphase Flow , 2002, 28 (9) : 1411-1435 DOI:10.1016/S0301-9322(02)00037-X |
| [13] | Chung P M, Kawaji M, Kawhara A . Two-phase flow through square and circular microchanels-effects of channel geometry[J]. Journal of Fluids Engineering , 2004, 126 (4) : 4575-4585 |
| [14] | Yang C-Y, Snieh C-C . Flow pattern of air-water and two-phase R-134a in small circular tubes[J]. International Journal of Multiphase Flow , 2001, 27 (7) : 1163-1177 DOI:10.1016/S0301-9322(00)00070-7 |
| [15] | Brackbill J U, Kothe D B, Zemach C . A continuum method for modeling surface tension[J]. Computer Physics , 1992, 100 (2) : 335-354 DOI:10.1016/0021-9991(92)90240-Y |
| [16] | JIA Zhi-hai(贾志海), LEI Wei(雷威), HE Ji-chang(贺吉昌) . Dynamic characteristics of vibrated-droplets on a microstructured hydrophobic surface(微结构疏水表面振动液滴的动态特性)[J]. Chinese Science Bulletin(科学通报) , 2014, 59 (27) : 2663-2667 DOI:10.1360/N972014-00022 |
| [17] | Zhang Tong, Cao Bin, Fan Yilin . Gas-liquid flow in circular microchannel(Part 1):Influence of liquid physical properties and channel diameter on flow patterns[J]. Chemical Engineering , 2011, 66 (23) : 5791-5803 DOI:10.1016/j.ces.2011.07.035 |
| [18] | Waelchi , von Rohr P R . Two phase flow characteristics in gas-liquid microreactors[J]. International Journal of Multiphase Flow , 2006, 32 (7) : 791-806 DOI:10.1016/j.ijmultiphaseflow.2006.02.014 |
| [19] | Xiong R, Chung J N . An experimental study of the size effect on adiabatic gas-liquid two-phase flow patterns and void fraction in microchannels[J]. Physics of Fluids , 2007, 19 (3) : 1139-1158 |
| [20] | Chi Y L, Sang Y L . Influence of surface wettability on transition of two-phase flow pattern in round mini-channels[J]. International Journal of Multiphase Flow , 2008, 34 (7) : 706-711 DOI:10.1016/j.ijmultiphaseflow.2008.01.002 |
| [21] | Chiwoong C, Dong I Y, Moohwan Kim . Surface wettability effect on flow pattern and pressure drop in adiabatic two-phase flows in rectangular microchannels with T-junction mixer[J]. Experimental Thermal and Fluid Science , 2011, 35 (6) : 1086-1096 DOI:10.1016/j.expthermflusci.2011.03.003 |
| [22] | Guan Ning, Liu Zhigang, Jiang Guilin . Experimental and theoretical investigations on the flow resistance reduction and slip flow in super-hydrophobic micro tubes[J]. Experimental Thermal and Fluid Science , 2015, 69 (3) : 45-57 |
| [23] | Thomas C, Chih-Ming H . Transport of bubbles in square microchannels[J]. Physics of Fluids , 2004, 16 (12) : 4575-4584 DOI:10.1063/1.1813871 |
| [24] | Can Ma, Yuan Huixin, Sun Leile . The impact of aspect rations on pressure drop in rectangular microchannel[J]. Chinese Hydraulics and Pneumatics , 2009, 1 : 17-19 |
| [25] | Zhao T S, Bi Q C . Co-current air-water two-phase flow patterns in vertical triangular microchannels[J]. International Journal of Multiphase Flow , 2001, 27 (5) : 765-782 DOI:10.1016/S0301-9322(00)00051-3 |
| [26] | Saisorn S, Wongwises S . An experimental investigation of two-phase air-water flow through a horizontal circular microchannel[J]. Experimental Thermal and Fluid Science , 2009, 33 (2) : 306-315 DOI:10.1016/j.expthermflusci.2008.09.009 |




