1 引言

固体颗粒悬浮液近年来在包括纳米颗粒合成、非均相催化反应、高分子聚合反应等微流控领域得到了越来越多的应用^[1~8]。以微反应器中的非均相催化反应为例，目前最常用的方法是将催化剂涂到反应器壁上，但这种方法只适用于部分催化剂且存在失活催化剂难以再生、更换等缺点。因而将催化剂颗粒直接悬浮于液体中在微反应器中进行反应的方法近来受到了越来越多的关注，而如何操控悬浮液在微反应器中流动以防止固体颗粒污染乃至堵塞微通道成为该技术的关键^[9~11]。当悬浮液在通道中流动时，剪切梯度会引起颗粒的跨流线迁移，从而导致颗粒在局部区域的聚集，这种现象在微通道中尤其显著^[12~17]。由于微通道的小尺度效应，使得流体的流动速度虽小，但剪切速率及其梯度却很大。目前文献中模拟悬浮液流动的模型主要包括两类，一类是基于扩散通量的Diffusive Flux Model (DFM)模型^{[15, 18]}，该模型认为颗粒迁移是由于不同区域颗粒之间的碰撞频率不平衡，因而其迁移通量随剪切速率梯度的增大而增大。另一类是基于质量和动量守恒的Suspension Balance Model (SBM)模型^[19~21]，该模型认为悬浮液中颗粒的迁移通量正比于其受到的法向应力。上述两种模型在模拟悬浮液流动及颗粒迁移方面都取得了许多成功，但目前的研究集中于常规尺度，对于悬浮液微尺度流动特性研究较少。

本文首先运用DFM模型模拟了毫米尺度通道中悬浮液的流动，通过与文献结果的对比，验证了模型的准确性。然后对直型微通道中悬浮液的流动进行模拟，通过与实验结果的比较，分析了由于微尺度效应，用于微通道中悬浮液的流动时需要对DFM模型所做的修正，确定了模型中的相关参数，最后探讨了颗粒直径、颗粒浓度、流动速度等各种参数对颗粒分布的影响。

2 数值方法 2.1 控制方程

本文研究对象为体积分数0.3~0.5的高浓度悬浮液，模拟中将分散颗粒和悬浮液体都看作连续介质，在Fluent中采用VOF(Volume of fluid)模型计算流体的输运过程，流体力学(CFD)模拟的控制方程包括混合物连续性方程、混合物动量传递方程和颗粒的质量传递方程。

混合物连续性方程为

$ \frac{{\partial \rho }}{{\partial t}} + \nabla \cdot \left( {\rho \boldsymbol{u}} \right) = 0 $

(1)

混合物动量传递方程为

$ \frac{\partial }{{\partial t}}\left( {\rho \boldsymbol{u}} \right) + \nabla \cdot \left( {\rho \boldsymbol{uu}} \right) =- \nabla p + \nabla \cdot \left( {\eta \left( \varphi \right){{\left[{\nabla \boldsymbol{u} + {{\left( {\nabla \boldsymbol{u}} \right)}^T}} \right]}_{}}} \right) + \rho g + F $

(2)

其中，ρ为悬浮液密度，u为速度矢量，p为压强，ρg为重力，F为其它体积力，因本文所研究的悬浮液流动过程中不受电场、磁场等外部场的影响，F仅需考虑分散颗粒和分散介质两相之间的相互作用力。η为悬浮液的黏度，根据Krieger^[24]提出的经验方程，按Eq.3计算。

$ \eta = {\eta _0}{\left( {1 - \frac{\varphi }{{{\varphi _{\rm{m}}}}}} \right)^{ - 1.82}} $

(3)

其中η₀为分散介质(液体)的黏度，Φ为颗粒体积分数，Φ_m为颗粒最大可能体积分数，其值为0.68^[18]。

颗粒的质量传递方程为

$ \frac{\partial }{{\partial t}}\left( {\rho \varphi } \right) + \nabla \cdot \left( {\rho \boldsymbol{u}\varphi } \right) =-\nabla \cdot \left( {{N_c} + {N_\eta } + {N_B}} \right) $

(4)

式中N_c称为碰撞通量(Eq.5)，表征颗粒因相互碰撞频率不平衡引起的颗粒由高剪切速率区域向低剪切速率区的迁移。

$ {N_{\rm{c}}} = - \rho {K_{\rm{c}}}{a^2}({\phi ^2}\nabla \dot \gamma {\rm{ + }}\dot \gamma \phi \nabla \phi ) $

(5)

Eq. 5中a为颗粒半径，K_c为碰撞系数，$\dot \gamma $为剪切速率。Eq.4中，N_η称为黏性通量(Eq.6)，表征由于黏度梯度引起的颗粒迁移通量的变化，因颗粒浓度高的区域黏度大，因而黏度通量抑制颗粒向高浓度区的迁移^[15]。

$ {N_\eta } = - \rho {K_\eta }\dot \gamma {\phi ^2}(\frac{{{a^2}}}{\eta })\frac{{{\rm{d}}\eta }}{{{\rm{d}}\phi }}\nabla \phi $

(6)

式中K_η为黏性系数。K_c与K_η为实验决定的经验常数，K_c/K_η的值需满足0 < K_c/ K_η < 1^[18]。Eq.4中，N_B为布朗通量，表征颗粒的布朗运动对颗粒迁移的影响，由式7计算。

$ {N_{\rm{B}}} = - {D_{\rm{B}}}\nabla \varphi = - \frac{{\dot \gamma {a^2}}}{{Pe}}\nabla \varphi $

(7)

其中D_B为扩散系数^[25]，Pe为péclet数(Eq.8)，表征剪切引起的颗粒迁移与布朗运动的相对大小，其值与颗粒直径及流体流速密切相关。当颗粒较大时，$ Pe \gg 1 $，布朗运动对颗粒迁移的影响可忽略，通常只有当颗粒的直径较小时，CFD计算中才需考虑布朗运动的影响^[26]。Eq.8中，k为玻尔兹曼常数。

$ Pe = \frac{{6\pi {\eta _0}\dot \gamma {a^3}}}{{kT}} $

(8)

2.2 剪切速率的修正

在使用DFM模型模拟悬浮液在直通道中的流动时，黏性通量N_η与剪切速率成正比。而在通道中心处，剪切速率为0，导致N_η也为0。其结果是通道中心的黏度增加并不能抑制粒子朝通道中心的迁移，导致颗粒体积分数Φ在通道中心处的数值发散。为了解决这个问题，Miller和Morris^[27]提出了一个非局部剪切速率的概念，即在剪切速率计算中，加上一项非局部剪切速率($ {\dot \gamma _{{\rm{NL}}}} $)，其值与颗粒直径与通道高度的相对大小ε和剪切速率有关(Eq.9)。

$ {\dot \gamma _{{\rm{NL}}}} = {a_s}(\varepsilon ){\dot \gamma _{\rm{s}}} $

(9)

其中a_S(ε)=ε²，ε=a/B，$ {\dot \gamma _s} = \frac{{{u_{\max }}}}{B} $，B为通道高度的一半，u_max为通道中心的速度。在$ \dot \gamma \to 0$的区域，$ {\dot \gamma _{{\rm{NL}}}} $为一较小的有限值，而在其他区域$ {\dot \gamma _{{\rm{NL}}}} \ll \dot \gamma $，因而非局部剪切速率的加入仅对通道中心附近产生影响。

2.3 求解过程

本文使用Fluent软件对上述方程组进行了求解，该软件基于有限体积计算方法，其标准求解方程形式为

$ \frac{\partial }{{\partial t}}{\rm{(}}\rho \varphi {\rm{) + }}\nabla \cdot (\rho \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over u} \varphi ){\rm{ = }}\nabla \cdot {\rm{(}}{\Gamma _\varphi }\nabla \varphi {\rm{) + }}{S_\varphi } $

(10)

其中φ为求解变量，$ \frac{\partial }{{\partial t}}{\rm{(}}\rho \varphi {\rm{)}} $为非稳态项，$ \nabla \cdot (\rho \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over u} \varphi )$为对流项，$ \nabla \cdot {\rm{(}}\Gamma \varphi \nabla \varphi {\rm{)}}$为扩散项，S_φ为源项，Г_φ为扩散系数。本文求解的三个方程中，连续性方程和动量方程符合Fluent求解方程的标准形式，而颗粒的质量传递方程Eq.4需变形为Eq.11。

$ \begin{array}{l} \frac{\partial }{{\partial t}}{\rm{(}}\rho \phi {\rm{) + }}\nabla \cdot (\rho \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over u} \phi ){\rm{ = }}\nabla \cdot ((\rho {K_\eta }(\dot \gamma {\rm{ + }}{{\dot \gamma }_{NL}}){\phi ^2}\frac{{{a^2}}}{\eta }\frac{{{\rm{d}}\eta }}{{{\rm{d}}\phi }}{\rm{ + }}{K_{\rm{B}}}\frac{{(\dot \gamma {\rm{ + }}{{\dot \gamma }_{{\rm{NL}}}}){a^2}}}{{Pe}})\nabla \phi )\\ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{}&{} \end{array}}&{}&{}&{} \end{array} + \nabla \cdot (\rho {K_{\rm{c}}}{a^2}({\phi ^2}\nabla (\dot \gamma {\rm{ + }}{{\dot \gamma }_{{\rm{NL}}}}) + (\dot \gamma {\rm{ + }}{{\dot \gamma }_{{\rm{NL}}}})\phi \nabla \phi )) \end{array} $

(11)

式中，扩散项为$ \nabla \cdot ((\rho {K_\eta }(\dot \gamma {\rm{ + }}{\dot \gamma _{{\rm{NL}}}}){\phi ^2}\frac{{{a^2}}}{\eta }\frac{{{\rm{d}}\eta }}{{{\rm{d}}\phi }}{\rm{ + }}{K_{\rm{B}}}\frac{{(\dot \gamma {\rm{ + }}{{\dot \gamma }_{{\rm{NL}}}}){a^2}}}{{Pe}})\nabla \phi ) $，源项为$ \nabla \cdot (\rho {K_{\rm{c}}}{a^2}({\phi ^2}\nabla (\dot \gamma + {\dot \gamma _{{\rm{NL}}}}) + (\dot \gamma + {\dot \gamma _{{\rm{NL}}}})\phi \nabla \phi )) $，在Fluent求解过程中需编写用户自定义函数(UDF)来分别定义。其中颗粒浓度($ \phi $)由一个用户自定义标量(UDS)代表^[28]，模拟过程中，Fluent提取每个控制体积的颗粒浓度，然后通过自带的梯度宏命令计算每个控制体积的颗粒体积分数梯度。之后，将编写的UDF导入FLUENT中进行编译，迭代求解Eq.1，Eq.2和Eq.11。

3 数值验证

为了证明建立的模拟方法及求解过程的正确性，研究中首先参考Lyon和Leal^[29]的实验研究，对悬浮液在图 1所示的矩形通道中的流动进行了模拟。该通道尺寸为L × H × W=304.8 mm (x) × 1 mm (y) × 50.8 mm (z)。由于通道宽度远大于通道高度，流体在流动过程中各参数在z方向的变化可以忽略，因此计算过程中进行x-y方向的二维模拟。

模拟过程中将计算区域分为200 (x) × 50 (y)个长方形控制体积。因流体的流动状态变化及颗粒的迁移主要发生通道入口处，而在通道后部逐渐达到稳态，因而设定的计算网格在通道入口处较为密集，沿着流动方向，网格密度越来越小，表现在x方向网格的长度呈倍数增长，第一个网格的长度是最后一个网格长度的1/100。

模拟中进口速度设为稳态时抛物线型速度分布；进口颗粒浓度为平均浓度；壁面采用无滑移边界条件，且壁面颗粒通量为0。因悬浮颗粒的直径较大，$ Pe \gg {\rm{ }}1 $，布朗运动对颗粒迁移的影响可以忽略。为了与文献[30]的结果相比较，非局部剪切速率采用Eq.9的形式^[27]。扩散系数参考文献[18]，取K_c=0.41，K_η=0.62。

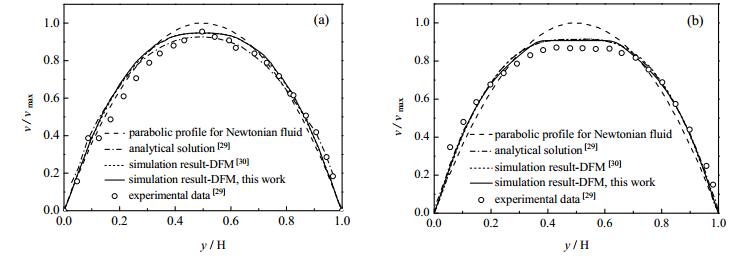
图 2显示了悬浮液在通道中稳态流动时的速度分布，图中的速度以最大速度为基准作了归一化处理。与牛顿流体的抛物线速度分布相比，悬浮液的速度分布在通道中心附近更为均匀。这是因为颗粒不断迁移至通道中心，导致通道中心附近颗粒的浓度不断增加，从而使该区域内流体的黏度增大，速度减小。与实验结果比较，CFD结果较准确地模拟了悬浮液的速度分布，且与文献中用解析法^[18]及CFD模拟^[30]得到的结果吻合也较好。

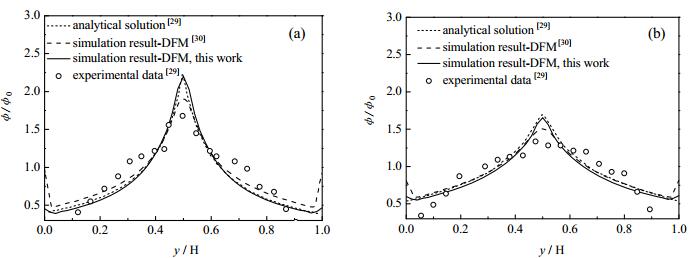
图 3显示了悬浮液在通道中稳态流动时的颗粒浓度分布。该图显示CFD模拟及解析法都能够预测颗粒在通道中心的聚集，但理论结果与实验结果相比，在近壁面处仍有一定差距。Lyon和Leal^[29]的实验结果是通过LDV技术间接得到的，其在近壁面处的测量精度尚需考证，因而近壁面处的颗粒浓度分布没有确凿数据可供参考。

4 悬浮液在直型微通道中流动的CFD模拟 4.1 计算过程与方法

在上节验证了建立的CFD模型准确性的基础上，本节运用DFM模型对悬浮液在微通道中的流动进行了模拟。参考文献[31]，直径为1.4 μm，微通道的尺寸为L × H × W=100 mm (x) × 0.05 mm (y) × 0.5 mm (z)。模拟中，计算区域被离散为2000 (x) × 50 (y)个长方体控制体积，x方向长度呈固定比例增长，最后一个网格与第一个网格长度之比为1000。

与上节相同，进口速度设为稳态时的抛物线型速度分布；进口颗粒浓度为平均浓度；壁面采用无滑移边界条件，且壁面颗粒通量为0。

4.2 模型参数的确定

悬浮液在微通道中的流动由于微尺度效应，流体剪切速率比宏观通道中大得多，因而用DFM模拟悬浮液在微通道中的流动时，Eq.11中的参数K_c、K_η以及非局部剪切速率的方程都需做相应修正。此外，因模拟的颗粒直径小，布朗运动对颗粒迁移通量的影响需明确。

4.2.1 K_c与K_η值的修正

K_c与K_η是由实验确定的经验常数。在对毫米级通道中悬浮液流动的模拟中，Miller等^[18]设定K_c=0.41，K_η=0.62。而本节模拟的为布朗悬浮液在微通道中的流动，需对K_c和K_η做适当调整。

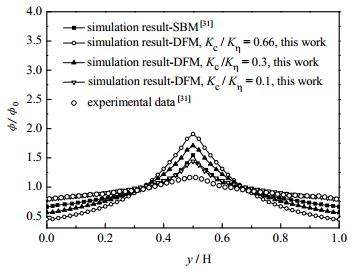
图 4为K_η=0.62时，不同K_c/K_η条件下微通道内颗粒浓度分布的CFD结果，并与文献的实验值及SBM模拟值进行了对比。从图中可以看出，DFM能准确预测粒子浓度在通道中心的聚集。然而当K_c/K_η=0.66时，CFD结果与实验结果存在较大差距，这是由于微尺度效应导致微通道中剪切速率梯度比宏观通道中大得多，因而根据Eq.5计算的颗粒碰撞通量过大。据此，研究中逐渐降低K_c的值，考察了不同K_c/K_η值时，微通道中颗粒的浓度分布。结果发现当K_c/K_η=0.1时，DFM-CFD模拟结果与实验结果相符更佳，与Semwogerer等^[31]的实验测量结果相比，他们使用SBM模型的模拟结果平均相对误差为10.25%，而当K_c/K_η=0.1时，本文使用修正DFM的模拟结果的平均相对误差仅为5.05%，可更好的预测微通道中颗粒浓度的分布。

4.2.2 非局部剪切速率的修正

因微通道中的剪切速率比宏观通道中大得多，非局部剪切速率的数值相应也要提高。为此我们提出了Eq.12的非局部剪切速率方程，式中Φ₀为颗粒的初始体积分数。与Millers等提出的校正方程Eq.9相比，Eq.12提出的非局部剪切速率与颗粒体积分数有关，粒子体积分数越大的区域，非局部剪切速率就越大。这样既可增大对通道中心颗粒聚集区剪切速率的校正，也能防止对通道其他区域剪切速率的过度修正。

$ {\dot \gamma _{{\rm{NL}}}} = \left( {\frac{a}{B}} \right){\left( {\frac{\phi }{{{\phi _0}}}} \right)^3}{\dot \gamma _{\rm{s}}} $

(12)

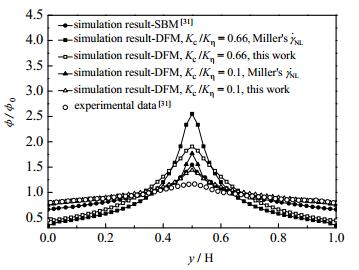
图 5为采用新的非局部剪切速率形式时，微通道中稳态颗粒浓度分布的CFD模拟结果。从图中可以看出，采用Eq.9的非局部剪切速率形式，颗粒在通道中心的浓度较大，与实验结果相差较大。而采用Eq.12的非局部剪切速率形式，颗粒浓度曲线在通道中心变得相对平坦，与实验结果的一致性更佳。当K_c/K_η=0.1时，使用Eq.12的非局部剪切速率代替Eq.9的非局部剪切速率，与实验结果相比^[31]，平均相对误差由5.39%降为5.05%。

4.3 悬浮液在直型微通道中流动的CFD模拟 4.3.1 悬浮液在微通道稳态流动时的速度分布

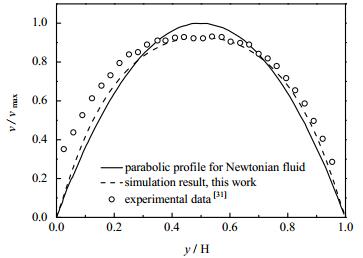
图 6显示了悬浮液在微通道中流动时的稳态速度分布。与毫米级通道相同，颗粒向通道中心的迁移导致该区域内流体的黏度增大，流动速度减小，因而速度分布在通道中心附近更为平缓，CFD结果与实验结果的一致性较好，与实验结果^[31]相比，平均相对误差仅为1.65%。

4.3.2 颗粒平均浓度对颗粒分布的影响

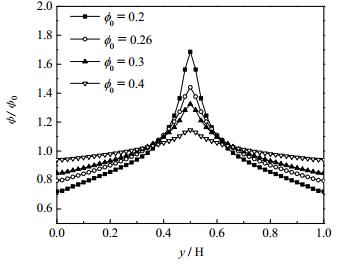
颗粒初始浓度对颗粒分布的影响如图 7所示。在通道中心处，颗粒的最大相对浓度(φ/φ₀)由1.69下降为1.15，且从图中可以看出，随着颗粒初始浓度的增大，稳态时颗粒浓度分布的均匀性增加。这是因为颗粒平均浓度越大，黏性产生的影响越大，从而抑制颗粒由低浓度区向高浓度区的迁移，这与Phillips^[18]及Lyon^[29]对非布朗颗粒悬浮液流动的实验研究结果一致。

4.3.3 颗粒粒径对颗粒分布的影响

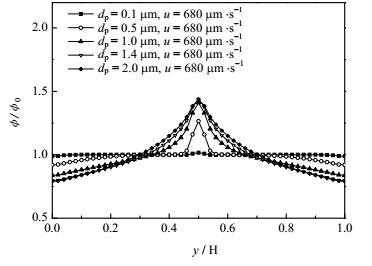
图 8比较了不同颗粒粒径时，微通道内稳态时颗粒的浓度分布。从图中可以看出，当颗粒粒径为0.1 μm时，颗粒浓度分布相对均匀，而随着颗粒粒径的变大，颗粒浓度分布变得越来越不均匀，如当颗粒粒径为0.5 μm时，通道中心处颗粒的最大相对浓度(φ/φ₀)达1.27，而通道中颗粒的最小相对浓度仅为0.92。且当颗粒粒径由0.5 μm增至1.0 μm时，通道中心处颗粒的最大相对浓度由1.27增加为1.41。但当d_p≥1 μm后，颗粒粒径的增大对颗粒浓度分布的影响变得不明显。

4.3.4 流动速度对颗粒分布的影响

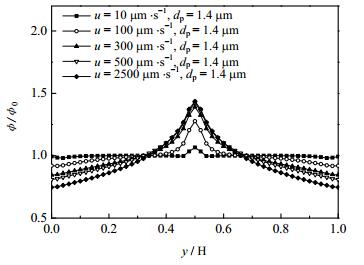
图 9比较了不同流速时，微通道内稳态时颗粒的浓度分布。从图中可以看出，当流速为10 μm·s^-1时，颗粒浓度分布相对均匀，而随着流速增大，颗粒浓度分布变得越来越不均匀，如当流速为100 μm·s^-1时，通道中心处颗粒的最大相对浓度(φ/φ₀)达1.28，而通道中颗粒的最小相对浓度仅为0.91。且流速由100 μm·s^-1增至300 μm·s^-1时，通道中心处颗粒的最大相对浓度由1.28变化到1.39。但当流速大于300 μm·s^-1时，增大流速对颗粒浓度分布的影响变得不明显。

4.3.5 不同Peclét准数下颗粒浓度分布的响应曲线

Peclét(Pe)准数表征剪切引起的颗粒迁移与布朗运动的相对大小。由Eq.8可知，Pe准数可以通过改变颗粒粒径和流速来调节。因此，将颗粒粒径与流体流速通过Pe准数量化出来，减小颗粒粒径和流速均能增大布朗运动的强度。

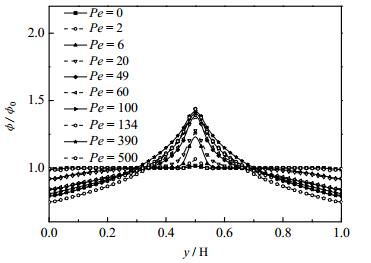
图 10比较了不同Peclét准数时，微通道内稳态时颗粒的浓度分布。从图中可以看出，随着Pe准数的增加，颗粒浓度分布越不均匀。这是因为Pe增大意味着剪切引起颗粒迁移的强度逐渐高于布朗运动强度，此时剪切力逐渐成为引起颗粒迁移的主要因素，因而颗粒浓度分布越不均匀。从图中还可以看出，当Pe < 100时，颗粒的浓度分布不均匀性随着Pe准数的增大而明显增加。而Pe ≥100时，随着Pe准数的继续增大，颗粒浓度分布变化并不明显。这是因为当Pe < 100时，布朗运动对于颗粒浓度分布仍具有一定影响。当Pe ≥100时，布朗运动相对于剪切作用变得可以忽略不计，因此再增大Pe准数的数值对颗粒浓度分布影响不大。

5 结论

本文采用修正后的Diffusive Flux Model对微通道中布朗粒子悬浮液的流动进行CFD模拟，研究了微尺度下布朗粒子悬浮液的流动特性，主要结论如下：

(1) 由于微通道中的微尺度效应，悬浮液在微通道中流动时的剪切速率较常规尺度通道中的要大的多，造成未修正的Diffusive Flux Model用于布朗颗粒悬浮液在微通道流动的数值模拟时有较大误差；

(2) 提出新的局部剪切速率形式，对Diffusive Flux Model进行相关修正。得到的数值结果显示，修正后的Diffusive Flux Model能够更好地描述微通道中布朗粒子悬浮液的流动。

(3) Peclét准数对微通道中颗粒浓度分布有着重要影响。当$ Pe \gg {\rm{ }}100 $时，布朗运动的影响可以忽略。而当$ Pe \ll {\rm{ }}1 $时，相比剪切引起的颗粒迁移，颗粒的布朗运动强度变得很大，从而抑制颗粒由通道壁向通道中心的迁移，颗粒的分布变得相对均匀。需要指出的是，本文主要贡献是对原有的Diffusive Flux Model模型做了尽可能在物理上有意义的修正，对于如何避免经验性和人为性将在未来的工作中做进一步深入的研究。