2. 工业大数据系统与应用北京市重点实验室,北京 100084;
3. 中国石油兰州化工研究中心,甘肃 兰州 730060
2. Beijing Key Laboratory of Industrial Big Data System and Application, Beijing 100084, China;
3. Lanzhou Petrochemical Research Center of Petrochina, Lanzhou 730060, China
化学工业中,动力学模型是常用的工具,其常见用途包括:反应速率常数计算,建立反应机理模型,计算不同组分产率随时间变化等。一旦知道了反应机理,上述化工问题常常在数学上可以利用微分方程进行描述,反应参数也可通过最小二乘法等进行处理[1]。然而,纯机理模型面临着一些困境。由于化工动力学系统的高度非线性性,动力学模型的求解往往会落入局部极值点。即使在一些反应机理已经明确的体系中,庞大微分方程组的数值计算往往也需要耗费大量的计算资源[2]。在实际研究与工业实践中,学者们大多使用集总模型以提高计算速度,但这样的模型也往往牺牲了特定组分的计算准确度[3]。
与纯机理模型相对应,部分学者在没有任何先验知识的前提下建立化学动力学模型,这类建模和计算方法通常基于深度神经网络这一强大的数学工具,用以实现生产能力与产物预测[4-5],操作条件优化[6],建立软测量模型[7]等。然而,训练完成后的多层神经网络往往只能在给定一组输入的前提下直接计算输出,而无法预测序列数据,如时序数据,或者产物沿管长分布等。如果使用深度神经网络来预测序列数据,则每一个原有的输入条件(如温度、压力等),将与上千个时间节点相关联,进而大大增加权重层中参数的数量,使得训练成本过高[4]。
针对这一问题,本文提出使用递归神经网络(RNN)的方法。近年来,随着计算机计算能力的进步和神经网络研究的发展,递归神经网络在自然语言处理问题(NLP)中获得了极大的成功。在文本生成[8],机器翻译[9],语音识别[10]等领域获得了广泛应用。本文首先讨论递归神经网络与深度神经网络的异同,和介绍递归网络建模与训练方法,说明了递归神经网络用于化工过程序列数据建模的可行性,然后提出了将递归神经网络应用于化工动力学建模的方法和实现步骤,并结合案例应用中验证了方法的优越性。
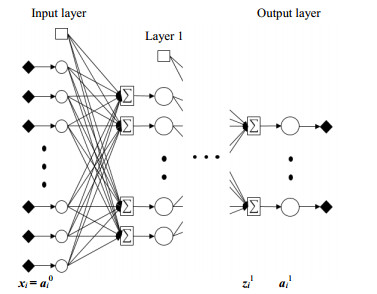
2 神经网络模型 2.1 深度神经网络模型一种常见的深度神经网络模型如图 1所示,数据信息只沿单一方向正向传播。每一处理单元被称为一个神经元。神经元首先计算前一层的输出信号的加权总和,加上偏置项,再通过激活函数产生输出进入下一层神经网络的计算。
|
图 1 深层神经网络结构 Fig.1 The structure of deep neural network |
一个多层神经网络的前向传播可用以下数学语言描述:
| $ \mathit{\boldsymbol{z}}_i^l = {W^l}\mathit{\boldsymbol{a}}_i^{(l - 1)} + {\mathit{\boldsymbol{b}}^l} $ | (1) |
| $ \mathit{\boldsymbol{a}}_i^l = {g^l}(\mathit{\boldsymbol{z}}_i^l) $ | (2) |
其中
| $ {\mathit{\boldsymbol{W}}^l} = \left[ {\begin{array}{*{20}{c}} {w_{1, 1}^l}&{w_{1, 2}^l}&{...}&{w_{1, {n_{l - 1}}}^l}\\ {w_{2, 1}^l}&{w_{2, 2}^l}&{...}&{w_{2, {n_{l - 1}}}^l}\\ \vdots & \vdots & \ddots & \vdots \\ {w_{{n_l}, 1}^l}&{w_{{n_l}, 2}^l}& \ldots &{w_{{n_l}, {n_{l - 1}}}^l} \end{array}} \right] $ | (3) |
| $ {g^l}(\mathit{\boldsymbol{z}}_i^l) = {(\sigma (\mathit{\boldsymbol{z}}_{(i, 1)}^l), \sigma (\mathit{\boldsymbol{z}}_{(i, 2)}^l), ...{\rm{, }}\sigma (\mathit{\boldsymbol{z}}_{(i, {n_l})}^l))^{\rm{T}}} $ | (4) |
权重系数矩阵Wl行数为第l层神经元个数nl,列数为第l-1层神经元个数nl-1。偏置项bl为该层所有神经元公用的常数。σ代表激活函数,常用的激活函数有Sigmoid函数与Relu函数等,其形式如下:
| $ S(z) = 1/(1 + {e^{ - z}}) $ | (5) |
| $ R(z) = \max \{ 0, z\} $ | (6) |
本文中建立的神经网络模型,在未加说明时默认使用Relu函数。研究证明,深度神经网络可以模拟任意的非线性系统,化工过程满足这一条件,通过构建合适的神经网络可以在确保运算精度的前提下避免复杂过程的求解,从而节省计算时间。一般而言,深层神经网络的模拟效果比浅层模型更好,但层数的增加往往也伴随着梯度爆炸或梯度消失的问题,使得训练更加困难。
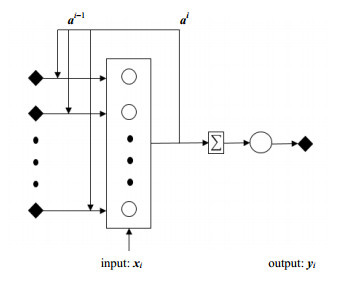
2.2 递归神经网络递归神经网络中,神经元的工作方式与深度神经网络基本一致。而深度神经网络中,所有的输入是相互独立的。这与许多化工过程中后一时刻的状态取决于前一时刻的状态的情况不符。与深度神经网络中数据的单向传递不同,递归神经网络(RNN)中,上一层计算的状态信息at-1将会进入下一层作为输入。可以形象地理解RNN方法能够“记忆”迄今为止计算的信息。从理论上讲,RNN可以以任意长的序列使用信息,但实际上它们仅限于回顾几步。图 2展示了一个典型的RNN结构,这一形态显示了数据不仅有向前传递的过程,也有循环使用的过程。而数据前向传播的公式则清晰地展示了完整序列数据的处理方式。
|
图 2 递归神经网络结构 Fig.2 The structure of recurrent neural network |
递归神经网络的前向传播公式如下:
| $ \mathit{\boldsymbol{a}}_i^t = {g_1}({\mathit{\boldsymbol{W}}_a}\mathit{\boldsymbol{aa}}_i^{(t - 1)} + {\mathit{\boldsymbol{W}}_{\rm{a}}}\mathit{\boldsymbol{xx}}_i^t + {\mathit{\boldsymbol{b}}_{\rm{a}}}) $ | (7) |
| $ \mathit{\boldsymbol{y}}_i^t = {g_2}({\mathit{\boldsymbol{W}}_{\rm{y}}}\mathit{\boldsymbol{aa}}_i^t + {\mathit{\boldsymbol{b}}_y}) $ | (8) |
式(7)可简化写为:
| $ \mathit{\boldsymbol{a}}_i^t = {g_{\rm{1}}}{\rm{(}}{\mathit{\boldsymbol{W}}_{\rm{a}}}[\mathit{\boldsymbol{a}}_i^{(t - 1)}, \mathit{\boldsymbol{x}}_i^t] + {\mathit{\boldsymbol{b}}_{\rm{a}}}) $ | (9) |
其中,
| $ {\mathit{\boldsymbol{W}}_{\rm{a}}} = [{\mathit{\boldsymbol{W}}_{{\rm{aa}}}}|{\mathit{\boldsymbol{W}}_{{\rm{a}}x}}] $ | (10) |
| $ [\mathit{\boldsymbol{a}}_i^{t - 1}, \mathit{\boldsymbol{x}}_i^t] = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{a}}_i^{t - 1}}\\ {\mathit{\boldsymbol{x}}_i^t} \end{array}} \right] $ | (11) |
xit是第i个样本在时间步t的输入,即第i组训练数据在t时刻的输入向量。例如,它可以表示多组分产率组成的向量,操作条件或工况信息等。
与深度神经网络在每一层使用不同的参数不同,RNN在所有步骤中共享相同的参数(Wa,Wya,g1,g2,…)。这意味着网络在每一步针对不同的输入都执行相同的任务,权重的共享机制大大减少了神经网络需要学习的参数总数,从而降低了模型的复杂度,并使RNN模型可以适应任意长度的序列数据输入,从而带来了更好的可推广性。
2.3 递归神经网络的训练网络的训练是一个优化问题,通过优化权重参数来最小化损失函数。由于建立预测模型往往是一个回归问题,可选取损失函数为预测值向量与理论值向量之间误差的平方和。
对于每个样本,
| $ L(\overline {{\mathit{\boldsymbol{y}}_i}} , {\mathit{\boldsymbol{y}}_i}) = \frac{1}{2}\sum\limits_{t = 1}^N {{{({{\mathit{\boldsymbol{\overline y}} }^t} - {\mathit{\boldsymbol{y}}^t})}^{\rm{T}}}({{\mathit{\boldsymbol{\overline y}} }^t} - {\mathit{\boldsymbol{y}}^t})} $ | (12) |
对于所有样本,
| $ J(w, b) = \frac{1}{m}\sum\limits_{i = 1}^m {L(\overline {{\mathit{\boldsymbol{y}}_i}} , {\mathit{\boldsymbol{y}}_i})} $ | (13) |
使用随机梯度下降法(SGD)训练参数,每次迭代权重和偏置值更新为
| $ {\mathit{\boldsymbol{W}}_{{\rm{ \mathsf{ θ} }} + 1}} = {\mathit{\boldsymbol{W}}_{\rm{ \mathsf{ θ} }}} - \alpha \frac{{\partial {J_\theta }}}{{\partial {\mathit{\boldsymbol{W}}_{\rm{ \mathsf{ θ} }}}}}, {\mathit{\boldsymbol{b}}_{{\rm{ \mathsf{ θ} }} + 1}} = {\mathit{\boldsymbol{b}}_{\rm{ \mathsf{ θ} }}} - \alpha \frac{{\partial {J_{\rm{ \mathsf{ θ} }}}}}{{\partial {\mathit{\boldsymbol{b}}_{\rm{ \mathsf{ θ} }}}}} $ | (14) |
其中,α为学习率。
| $ \frac{{\partial {J_{\rm{ \mathsf{ θ} }}}}}{{\partial {\mathit{\boldsymbol{W}}_{\rm{ \mathsf{ θ} }}}}} = \frac{1}{m}\sum\limits_{i = 1}^m {\frac{{\partial {L_{\rm{ \mathsf{ θ} }}}}}{{\partial {\mathit{\boldsymbol{W}}_{\rm{ \mathsf{ θ} }}}}} = } \frac{1}{m}\sum\limits_{i = 1}^m {\sum\limits_{t = 1}^N {\frac{{\partial L_{\rm{ \mathsf{ θ} }}^t}}{{\partial {\mathit{\boldsymbol{W}}_{\rm{ \mathsf{ θ} }}}}}} } $ | (15) |
单一样本的梯度
| $ \frac{{\partial L_{\rm{ \mathsf{ θ} }}^t}}{{\partial {\mathit{\boldsymbol{W}}_y}}} = \frac{{\partial L_{\rm{ \mathsf{ θ} }}^t}}{{\partial {{\mathit{\boldsymbol{\overline y}} }^t}}}\frac{{\partial {{\mathit{\boldsymbol{\overline y}} }^t}}}{{\partial {\mathit{\boldsymbol{a}}^t}}}\frac{{\partial {\mathit{\boldsymbol{a}}^t}}}{{\partial {\mathit{\boldsymbol{W}}_y}}} = {({\mathit{\boldsymbol{\overline y}} ^t} - {\mathit{\boldsymbol{y}}^t})^T} \times {a^t} $ | (16) |
对于Wa,(即[Waa|Wax]),计算则更加复杂。使用链式法则,可知
| $ \frac{{\partial L_{\rm{ \mathsf{ θ} }}^t}}{{\partial {\mathit{\boldsymbol{W}}_{\rm{a}}}}} = \frac{{\partial L_{\rm{ \mathsf{ θ} }}^t}}{{\partial {{\mathit{\boldsymbol{\overline y}} }^t}}}\frac{{\partial {{\mathit{\boldsymbol{\overline y}} }^t}}}{{\partial {\mathit{\boldsymbol{a}}^t}}}\frac{{\partial {\mathit{\boldsymbol{a}}^t}}}{{\partial {\mathit{\boldsymbol{W}}_{\rm{a}}}}} $ | (17) |
由于ait= g1(Wa[ait-1, xit]+ba),可知at的求导取决于at-1, at-2, …, a0而at-1也是Wa的因变量,而不能认为是常数,所以该梯度的实际计算式为:
| $ \frac{{\partial L_{\rm{ \mathsf{ θ} }}^t}}{{\partial {\mathit{\boldsymbol{W}}_{\rm{a}}}}} = \sum\limits_{k = 0}^{t - 1} {\frac{{\partial L_{\rm{ \mathsf{ θ} }}^t}}{{\partial {{\mathit{\boldsymbol{\overline y}} }^t}}}} \frac{{\partial {{\mathit{\boldsymbol{\overline y}} }^t}}}{{\partial {\mathit{\boldsymbol{a}}^t}}}\frac{{\partial {\mathit{\boldsymbol{a}}^t}}}{{\partial {\mathit{\boldsymbol{a}}^k}}}\frac{{\partial {\mathit{\boldsymbol{a}}^k}}}{{\partial {\mathit{\boldsymbol{W}}_{\rm{a}}}}} $ | (18) |
| $ \frac{{\partial {\mathit{\boldsymbol{a}}^t}}}{{\partial {\mathit{\boldsymbol{a}}^k}}} = \prod\limits_{j = k + 1}^t {\frac{{\partial {\mathit{\boldsymbol{a}}^j}}}{{\partial {\mathit{\boldsymbol{a}}^{j - 1}}}}} $ | (19) |
| $ \frac{{\partial L_{\rm{ \mathsf{ θ} }}^t}}{{\partial {\mathit{\boldsymbol{W}}_{\rm{a}}}}} = \sum\limits_{k = 0}^{t - 1} {\frac{{\partial L_{\rm{ \mathsf{ θ} }}^t}}{{\partial {{\mathit{\boldsymbol{\overline y}} }^t}}}} \frac{{\partial {{\mathit{\boldsymbol{\overline y}} }^t}}}{{\partial {\mathit{\boldsymbol{a}}^t}}}(\prod\limits_{j = k + 1}^t {\frac{{\partial {\mathit{\boldsymbol{a}}^j}}}{{\partial {\mathit{\boldsymbol{a}}^{j - 1}}}}} )\frac{{\partial {{\rm{a}}^k}}}{{\partial {\mathit{\boldsymbol{W}}_{\rm{a}}}}} $ | (20) |
在传统的反向传播算法(Back Propagation,简称BP算法)中,由于没有参数共享,所以每一层的梯度不需要加和。而在RNN的网络训练中,每一时间序列层相互之间存在影响,因此这一参数训练方法又被称为BPTT算法(back propagation through time)[11]。从公式(20)可以看出,计算一层的梯度需要考虑之前所有层的梯度。在实际训练时,往往将k值截断在一个固定可接受的长度, 在本文后续建立的模型中,默认截断长度为100。
3 递归神经网络在化工反应过程中的应用在化工反应过程模拟中,动态过程的反应物和产物组成,随时间变化而产生序列数据,分布参数建模中,反应物与产物组成随空间位置变化而产生序列数据。由于这些时序数据与空间序列数据的产生都受到前序数据的影响,因此可以利用递归神经网络建立过程模型。以下通过3个具体案例,说明构建递归神经网络模型的方式和步骤。
3.1 案例1:多组分时序产率预测工业实践中,往往需要对反应器中的物质浓度进行实时监测。对此类反应往往已经有一定先验知识,化工过程往往也伴随操作条件突然变化以及测量过程中的噪音等。在该案例中,探讨一个简单的连续反应化工过程,其化学方程式可简化为:
| $ \mathrm{A} \stackrel{k_{1}}{\longrightarrow} \mathrm{B} \stackrel{k_{2}}{\longrightarrow} \mathrm{C} $ | (21) |
要求A, B, C 3类物质的浓度变化,不难得出其满足的微分方程为
| $ \frac{\mathrm{d}[\mathrm{A}]}{\mathrm{d} t}=-k_{1}[\mathrm{A}] $ | (22) |
| $ \frac{\mathrm{d}[\mathrm{B}]}{\mathrm{d} t}=k_{1}[\mathrm{A}]-k_{2}[\mathrm{B}] $ | (23) |
| $ \frac{\mathrm{d}[\mathrm{C}]}{\mathrm{d} t}=k_{2}[\mathrm{B}] $ | (24) |
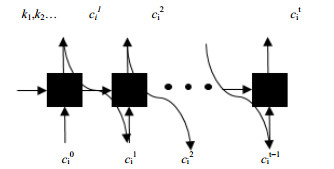
令[A]0 = 1 mol·L-1,[B]0 = [C]0 = 0, k1, 2为反应速率常数,在构造训练样本时,假定其为0~1的随机数。模型的工作原理如图 3所示,计算3种物质在10 min内的浓度变化,将其分为100个小的时间间隔,神经网络的输入包括反应速率常数以及3个反应物上一时刻浓度(0~99时刻),输出为下一时刻浓度(1~100时刻)随时间的变化,其中反应速率常数k1, k2作为t0时刻的状态量输入。
|
图 3 多组分时序产率预测模型 Fig.3 Scheme of the multicomponent time series prediction model |
正确选择神经网络的隐含单元数量是模型取得较好精度的关键。当隐含单元过少时,模型没有足够的自由度处理复杂问题。当隐含单元数量过多时,待拟合的参数数量也会增加,由于这些参数在初始化时都是随机给定的,因此,模型的训练将会耗费更多的时间并有可能出现过拟合的现象。鉴于一定数量的隐藏单元对于网络计算非线性函数是必要的,在训练阶段,必须首先确定合适的隐藏单元数量。
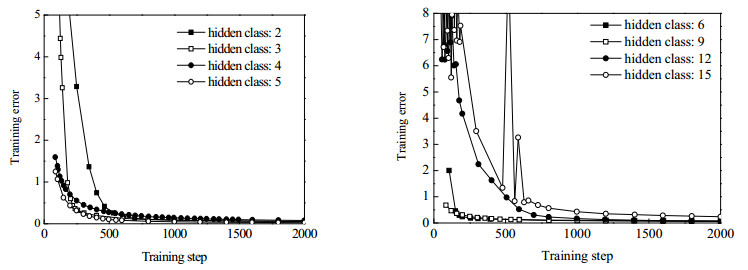
图 4罗列了当单元数从2至15时的训练曲线,可见当训练到1 000步时,所有模型在训练集上的误差都可以下降到其误差平方和小于0.5。表 1列出了不同网络结构在一定步数下误差的收敛情况。可以看出,当隐藏单元数小于5时,训练步数为149时,误差函数随隐藏层单元数的增加而减小,网络收敛更快。选择第149步的依据是,当步数过小时,4个模型均未收敛,当步数过大时,模型均已收敛从而无法对收敛快慢做出比较。当隐藏单元数大于5时,选择第199步训练情况进行比较,这是因为网络中随机化的初始参数过多,训练还未达到稳定状态,从而使得预测结果有很大的随机性。此时,误差函数反而随隐藏层单元数的增加而增大,网络的表现并没有得到明显的提高。可以看出,过多的隐藏单元数不仅造成了训练成本的增加,并且容易造成数据过拟合的情况出现。因此,在这个案例中,设定最好的隐藏单元数为5。
|
图 4 网络训练误差与隐藏单元数的变化关系 Fig.4 The relationship between network training error and the number of hidden units |
|
|
表 1 训练初期不同隐藏单元的训练误差 Table 1 Training errors of different hidden units at the beginning |
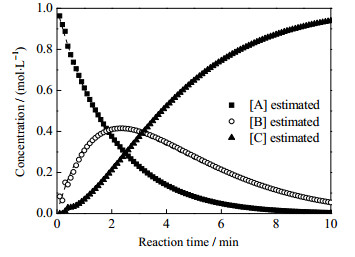
训练完成的网络可以预测平稳状态下的多组分产率。如图 5所示,假定一组连续反应中k1 = 0.5,k2 = 0.4时进行模拟,则根据式(21)~(23),可以得到3种物质随时间变化的曲线。
|
图 5 连续反应下多组分产率变化 Fig.5 Profiles of multicomponent yield under continuous reaction |
可以观察到,网络的预测值与理论值有相当好的一致性。
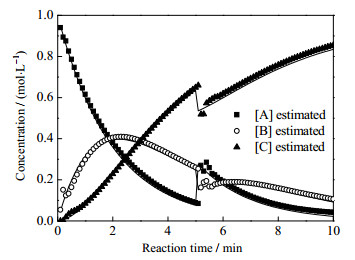
图 6则展示了当操作出现扰动时,如5 min时,由于操作条件改变,组分A浓度上升,而组分B,C浓度下降,网络也能较好地预测不同物质的变化行为与变化趋势。
|
图 6 多组分产率操作条件的变化 Fig.6 Profiles of operating condition under continuous reaction |
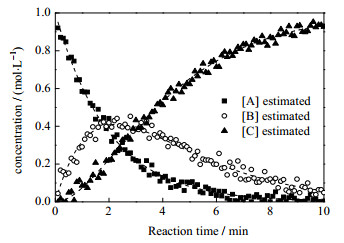
然而,在实际过程中,测量方式导致的噪声往往不可避免,因此,对测试数据引入高斯噪声,模型的表现如图 7所示,噪声的确造成了曲线一定幅度的波动,但递归神经网络仍然可以较好地预测产物浓度随时间变化的趋势。
|
图 7 引入高斯噪声后多组分产率变化 Fig.7 Profiles of multicomponent yield after adding Gaussian noise |
在工业过程中,一些关键参数往往难以实时在线测量,对过程的建模和控制相对比较复杂,因此纯机理模型难以建立。而应用递归神经网络则可以构造黑箱模型,对这些参数进行预测,而建立该过程的自适应控制系统。
3.2 案例2:反应速率常数回归比连续反应更复杂的反应模式是带回路的循环反应模型:
| $ \mathrm{A} \stackrel{k_{1}}{\longrightarrow} \mathrm{B} \stackrel{k_{2}}{\longrightarrow} \mathrm{C} \stackrel{k_{3}}{\longrightarrow} \mathrm{A} $ | (25) |
与上例类似,递归神经网络同样可以在给定反应速率常数的情况下模拟多组分的产率随时间变化趋势(图 8)。

|
图 8 循环反应下多组分产率变化 Fig.8 Profiles of multicomponent yield under cyclic reaction |
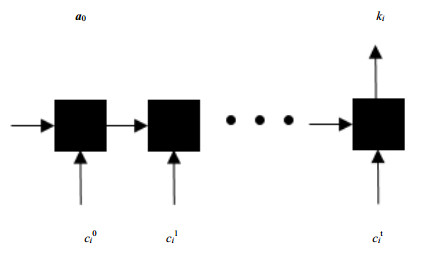
在这个案例中,研究将产率随时间变化作为输入,将反应速率常数作为输出的可能。使用实验数据来直接预测反应速率常数,而不需要解微分方程或者动力学反应的知识,并可以大大减少实验次数。案例中的神经网络结构参考了计算机视觉领域中的图像分类以及自然语言处理中的文本情感分析等N输入:1输出场景。模型仍然使用权重共享处理序列数据,且上一层的状态信息会进入下一层进行计算。然而,与之前案例每一时刻均有一个有效输出不同,这个案例只有最后的输出是有实际物理意义的,即代表反应速率常数。模型的工作原理如图 9所示,输入为A,B,C 3种物质在10 min内的浓度变化(均匀分割为100个时间点作为输入),输出为3个反应速率常数。采取与上例类似策略,设定隐含单元数量为15。
|
图 9 反应速率常数回归模型 Fig.9 Scheme of the reaction rate constant regression model |
a0为维数与隐藏单元数数值相同的零向量。训练集中的输入-输出对为:
| $ {\mathit{\boldsymbol{X}}_i} = \left[ {\begin{array}{*{20}{c}} {[{\rm{A}}]_i^1}&{[{\rm{A}}]_i^2}& \cdots \\ {[{\rm{B}}]_i^1}&{[{\rm{B}}]_i^2}& \cdots \\ {[{\rm{C}}]_i^t}&{[{\rm{C}}]_i^2}& \cdots \end{array}\begin{array}{*{20}{c}} {[A]_i^t}\\ {[B]_i^t}\\ {[C]_i^t} \end{array}} \right], {\mathit{\boldsymbol{Y}}_i} = \left[ {\begin{array}{*{20}{c}} {k_i^1}\\ {k_i^2}\\ {k_i^3} \end{array}} \right] $ | (26) |
由于模型的向量化实现,实际的X的是一个由样本数、时间序列长度、组分数组成的三维向量(500×100×3)。本文利用不同的k1,k2,k3,产生了500个样本用于模型训练,而在实际操作中,样本可来自实验或工业数据。
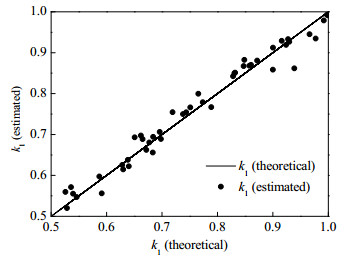
训练后的网络在测试集(50个样本点)上取得了很好的一致性。图 10展示了k1预测值和实际值之间的吻合情况。
|
图 10 k1理论值与计算值在测试集上的一致性 Fig.10 Consistency of k1's theoretical value and calculated value in test set |
其余速率常数的回归公式如下:
| $ {k_{{\rm{1, est}}}} = {0.993_{}}{\rm{1}}{k_{{\rm{1, }}}}_{{\rm{the}}} + {0.004_{}}6{, _{}}R = {0.985_{}}1 $ | (27) |
| $ {k_{{\rm{2, est}}}} = {0.941_{}}3{k_{{\rm{2, the}}}} + {0.030_{}}6{, _{}}R = {0.969_{}}0 $ | (28) |
| $ {k_{{\rm{3, est}}}} = 1.037{k_{{\rm{3, the}}}} - {0.018_{}}2{, _{}}R = {0.955_{}}1 $ | (29) |
其中,kest代表模型预测值,kthe代表理论值。线性回归的结果清晰地展示了训练后的递归神经网络通过组成数据可以较精确地预测动力学常数,如反应速率常数,就体现了良好的一致性。使用递归神经网络求解反应速率常数,可以避免求解微分方程的求解。随着反应网络的庞大化,这项优势可以大大减小计算所需时长。
3.3 案例3:工业油田轻烃裂解装置模拟与优化上述两个案例探讨了反应网络中的典型反应模式,在这个案例中,将研究递归神经网络在大规模反应网络中的工业应用。
乙烯是有机化工工业重要的原料,其制取对我国化工工业具有重要的意义。在蒸汽热裂解制乙烯的过程中,油田轻烃是相对优质的裂解原料。模拟乙烯裂解是一个复杂的建模过程。已有学者对轻烃裂解网络做出了研究,提出了包含39种物质与自由基,340个反应的简化基元反应网络模型[12]。在此基础上,有学者提出对裂解装置的辐射段进行建模,通过建立原料分子重构模型,过程微分方程结合反应网络,构建管式反应器过程模型[13]。
| $ \frac{{d{N_{{\rm{in}}}}}}{{dL}} = \frac{1}{L}\sum\limits_i {{v_{{\rm{in}}}}{r_i}} $ | (30) |
对于这类刚性方程组,通常采用数值型解法通过迭代方式获得稳定解,从而得到裂解产物组成。但这类方法受步长,初值等影响较大,有时会出现长时间无法收敛的情况。而递归神经网络方法则有效地避免了此类问题,从而加快了计算速度。
例如式(30)所示的质量平衡方程式中,Nin表示物质n的摩尔流率,mol·s-1;L表示反应炉管长度,m;vin表示关于物质n的第i个反应式的反应计量系数;ri表示反应i的反应速率。由于求解的常微分方程组中含有大量的反应方程,反应系数之间数量级差距较大,使得整个方程组条件数较大。
对于这类刚性方程组,通常采用数值型解法通过迭代方式获得稳定解,从而得到裂解产物组成。但这类方法受步长,初值等影响较大,有时会出现长时间无法收敛的情况。
本文使用这一现有纯机理模型,利用同一原料在不同进料量与出口温度下模拟得到的产物沿管长分布数据作为训练样本。原料信息与操作条件变化范围如表 2所示。
|
|
表 2 训练集原料信息与操作条件 Table 2 Feed information and operating conditions of training set |
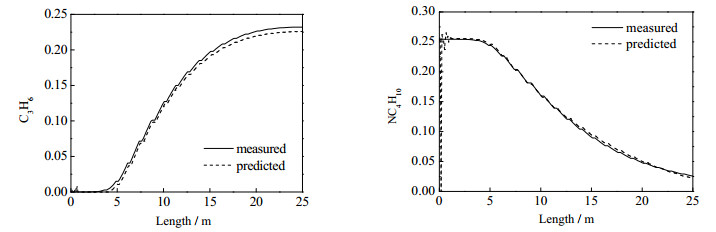
已有文献证明[14],这一工业过程的典型操作条件包括进料量,出口温度,水油比,进口压力等等。递归神经网络将进料量与出口温度这两个操作条件作为变量输入,在工作区间内随机取点,共生成2 000组数据。在此训练集基础上,递归神经网络拟合产物沿管长分布的产率数据。与前两个案例不同,前者的数据是物质浓度随时间的变化,且反应模式较为简单,本案例选取的数据在空间上的离散分布,且反应网络更复杂。图 11展示了在验证样本中,主要产物收率沿管长的变化趋势,实线为机理模型收率分布,虚线为递归神经网络预测值,可以看出后者的预测结果与前者相对误差较小,但由于工业案例计算难度较大,部分产物存在静差的现象,说明训练还存在一定问题。
|
图 11 正丁烷与丙烯的沿管长分布收率 Fig.11 Yield profiles of n-butane and propylene along the length of the tube units |
原有机理模型计算的重点与难点在于对炉管进行分段后,需要求解的庞大微分方程组,也就是质量平衡、动量平衡和能量平衡方程组。求解时需要先获取所研究的炉型设备尺寸和相应的反应网络及参数,并将重要操作参数如辐射段裂解气出入口温度压力等作为已知条件输入。
案例通过比较两类模型的运行时间,发现递归神经网络可以极大地缩短计算时长。在100次随机运算中,纯机理模型需要计算平均9.266 s才能达到收敛,而RNN网络模型平均只需0.079 32 s。这是因为机理模型在耦合迭代过程中,需要求解庞大的质量平衡、动量平衡、能量平衡微分方程组,而RNN模型则节省了这一笔计算开支。
在这一研究基础上,模型预测的快速计算速度为操作条件的优化选择提供了可能,因为优化往往需要对一定范围内的输入进行多次计算,方能选取对于目标函数的最优值。
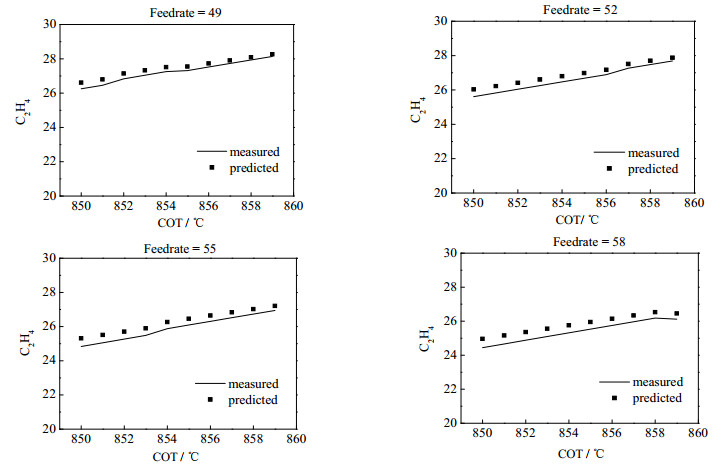
本例选取重要产物乙烯的最终收率最大化作为目标,对COT从850到860 ℃,每隔1 ℃取点,对进料量从49到59 t·h-1每隔1 t·h-1取点,做了共100次运算,图 12展示了运算结果。
|
图 12 不同操作条件下乙烯产率 Fig.12 Ethylene yields under different operating conditions |
计算表明,当此套工业装置在COT为850~860 ℃,进料量为49~59 t·h-1的条件下运行时,乙烯收率随出口温度的升高而升高,随进料量的升高而降低。这是因为当出口裂解温度升高时,炉膛加强了对管内反应的传热,使反应进行得更快从而使乙烯收率提高。当进料量提高时,物料停留时间变小,而传热强度并不能满足管内裂解反应的需要,导致乙烯收率变低。RNN网络模型对此提供了很好的趋势预测,与现有文献的结论相一致[14]。
4 结论与展望本文探讨了递归神经网络的工作原理,训练算法以及其在化工过程建模中的应用,共研究了3个可应用的场景:化学反应中物质浓度的时序变化,反应动力学参数回归,油田轻烃裂解过程模拟以及操作条件优化。递归神经网络在这3种案例中都取得了良好的表现。
通过案例,本文研究RNN在化工动力学建模中的适用性,评估其模拟效果并为RNN在工业实践中的应用提供一般的指导,结果证明递归神经网络是建立复杂和高度非线性化工动力学模型的合适工具。虽然普通RNN网络在计算梯度时往往只计算有限步以内的梯度,且噪声可能会造成模型的波动从而影响精确性,但随着计算机计算能力的提高,有更多复杂RNN模型,如多层RNN、LSTM模型等等,可以更有效地处理海量工业数据,对于更加庞大且需要长周期预测的化工体系,达到更好的预测精度。
符号说明:
|
|
| [1] |
VAJDA S, RABIRZ H. Identifiability and distinguishability of general reaction systems[J]. Journal of Physical Chemistry, 1994, 98(20): 5265-5271. DOI:10.1021/j100071a016 |
| [2] |
CONNORS K A. Chemical kinetics: The study of reaction rates in solution[M]. New York: John Wiley & Sons, 1990.
|
| [3] |
WHITE J E, CATALLO W J, LEGENDRE B L. Biomass pyrolysis kinetics: A comparative critical review with relevant agricultural residue case studies[J]. Journal of Analytical and Applied Pyrolysis, 2001, 91(1): 1-33. |
| [4] |
HOUGH B R, BECK D A C, SCHWARTZ D T, et al. Application of machine learning to pyrolysis reaction networks: Reducing model solution time to enable process optimization[J]. Computers & Chemical Engineering, 2017, 104: 56-63. |
| [5] |
ZHANG M, LIU X, ZHANG Z. A soft sensor for industrial melt index prediction based on evolutionary extreme learning machine[J]. Computers & Chemical Engineering, 2016, 24: 1013-1019. |
| [6] |
SHI B, YANG X, YAN L. Optimization of a crude distillation unit using a combination of wavelet neural network and line-up competition algorithm[J]. Chinese Journal of Chemical Engineering, 2017, 25(8): 1013-1021. DOI:10.1016/j.cjche.2017.03.035 |
| [7] |
王玉乔, 程光旭, 汤杰国. 基于KPCA的连续重整催化剂结焦碳含量软测量模型[J]. 高校化学工程学报, 2009, 23(5): 852-857. WANG Y Q, CHENG G X, TANG J G. KPCA based soft-sensing model of carbon content of catalyst coking in continuous catalytic reforming reactors[J]. Journal of Chemical Engineering of Chinese Universities, 2009, 23(5): 852-857. DOI:10.3321/j.issn:1003-9015.2009.05.022 |
| [8] |
ZHANG J, DAN Q U, ZHEN L I. Recurrent neural network language model based on word vector features[J]. Pattern Recognition & Artificial Intelligence, 2015, 28(4): 299-305. |
| [9] |
GUZMAN F, JOTY S, MARQUEZ L, et al. Machine translation evaluation with neural networks[J]. Computer Speech & Language, 2017, 45: 180-200. |
| [10] |
OGAWA A, HORI T. Error detection and accuracy estimation in automatic speech recognition using deep bidirectional recurrent neural networks[J]. Speech Communication, 2017, 89: 70-83. DOI:10.1016/j.specom.2017.02.009 |
| [11] |
SU H T, MCAVOY T J, WERBOS P. Long-term predictions of chemical processes using recurrent neural networks: A parallel training approach[J]. Industrial & Engineering Chemistry Research, 1992, 31(5): 1338-1352. |
| [12] |
张磊, 陈丙珍, 邱彤. 基于PCA的反应网络简化策略[J]. 化工学报, 2011, 62(1): 137-141. ZHANG L, CHEN B Z, QIU T. Reaction network model reduction based on PCA[J]. CIESC Journal, 2011, 62(1): 137-141. |
| [13] |
FANG Z, QIU T, CHEN B Z. Improvement of ethylene cracking reaction network with network flow analysis algorithm[J]. Computers & Chemical Engineering, 2016, 91: 182-194. |
| [14] |
胡益锋, 徐用懋, 何细藕. 石脑油裂解炉动态建模与仿真研究[J]. 石油学报(石油加工), 2004, 20(6): 51-57. HU Y F, XU Y M, HE X O. The dynamic modeling and simulation of naphtha pyrolysis furnace[J]. Acta Petrolei Sinica (Petroleum Processing Section), 2004, 20(6): 51-57. DOI:10.3969/j.issn.1001-8719.2004.06.009 |




