膜分离技术广泛应用于环境、化工等领域,是当今分离科学中最重要的手段之一[1]。柱式膜组件比表面积大、设备体积小、适用范围广等优点,广泛应用在石油化工、医药、水处理等领域[2, 3]。作为膜分离应用的基本单元,膜组件在构型与操作条件的优化设计方面将直接影响膜分离应用的能力和效率。
近年来,计算流体力学(Computational Fluid Dynamics,CFD)应用于膜组件优化设计得到了快速发展[4],主要包括:中空纤维膜组件结构与操作优化设计、陶瓷膜结构优化设计等。为了研究外压式中空纤维膜组件进出口位置对膜组件内壁面剪应力与压降的影响,Kaya等[5]利用CFD软件对膜组件进行了计算模拟。但是,在计算模拟中仅仅考虑了200多根膜丝且不考虑膜丝摆动与渗透性能。杨毅等[6]通过引入新的算法对中空纤维膜组件壳程内膜丝摆动对壳程内部流场的影响进行了研究。但是,在计算模拟中仅考虑少量膜丝且没有考虑膜丝渗透性能。Buetehorn等[7]研究了分别在单相流与两相流条件下,浸没式膜生物反应器中膜组件内部流场的的特性。研究中考虑了膜丝的摆动、多孔性以及摩察系数等膜组件特性,但是这些数值仅仅建立在膜丝某一瞬间位置的基础上,具有一定的偶然性。Cai等[8]将整个膜丝填充区视为一个多孔介质区,采用多孔介质模型对膜组件内部流场进行了计算模拟。采用多孔介质方法不仅减少模型建立难度,同时降低了对计算资源需求。本课题组在膜组件的优化设计方面也做了许多工作积累,彭文博等[9, 10]将陶瓷膜视为多孔介质,采用CFD方法对多通道陶瓷膜的过滤行为进行了系统研究,研究结果为陶瓷膜组件结构的优化设计提供了理论指导。邹琳玲等[11]采用CFD技术对恒通量陶瓷膜的厚度也做了相关的优化设计工作。
到目前为止,在优化设计柱式膜组件分布器构型、操作条件等方面的研究工作还鲜有报道。本文旨在采用欧拉模型与多孔介质模型,通过CFD软件计算模拟出柱式膜组件在曝气过程中气液两相流场的特点,从而为柱式膜组件分布器构型与操作条件的优化设计提供理论指导。
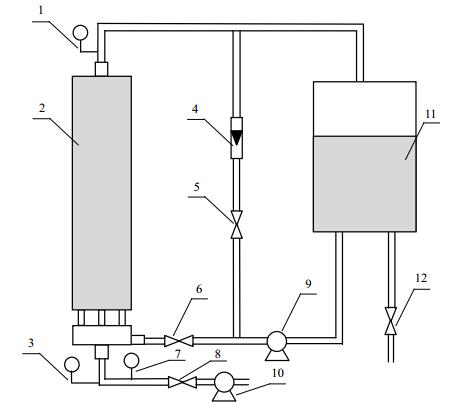
2 实验部分实验装置如图 1所示,膜组件进口管直径40 mm,长50 mm;气液分布管管径125 mm,高度50 mm;曝气孔直径10 mm,高度50 mm;膜丝装填区管径125 mm,高度1000 mm;出口管直径40 mm,高度50 mm。组件内液相为水,气相为空气。
|
图 1 实验装置流程图 Fig.1 Schematic diagram of the experimental setup 1. pressure gage 2. membrane module 3. pressure gage 4. flowmeter 5, 6, 8, 12. valve 7. flowmeter 9. pump 10. air compressor 11.water |
为了再现对膜组件曝气过程中气液两相流流动过程。设定如下实验流程:关闭阀门12和8,打开阀门6,使用离心泵将水注满膜组件,并且形成回路;关闭离心泵和阀门6,用阀门8调节气量至一定值,压缩空气经过气体流量计7,进入到膜组件的进口管,气体依次经过气液分布管、曝气孔在膜丝填充区域内形成曝气过程,排出的气液混合物进入到水槽。
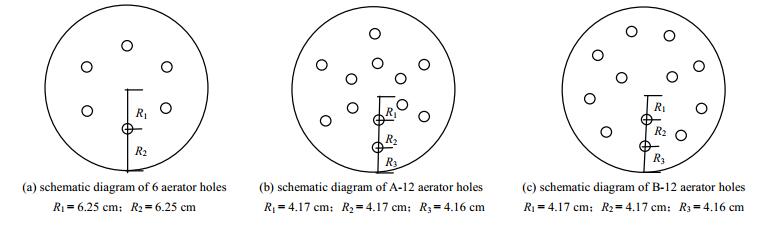
4柱式膜组件分布器构型(一个黑色小圆圈代表一个曝气孔,曝气孔直径为10 mm)如图 2所示,图 2(a)为柱式膜组件分布器6曝气孔的示意图,图 2 (b)和(c)分别为柱式膜组件A-12、B-12型分布器12曝气孔的示意图。
|
图 2 柱式膜组件分布器示意图 Fig.2 Schematic diagram of distributors of membrane modules |
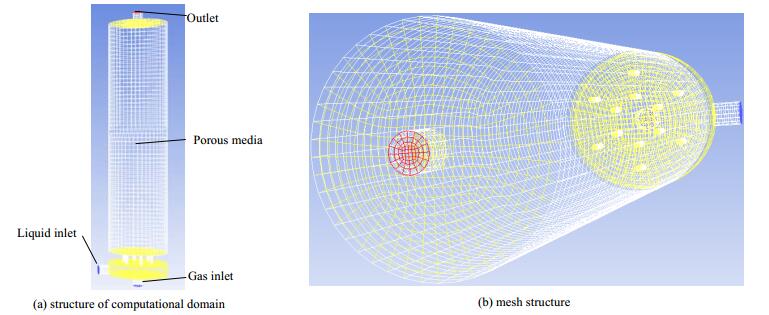
如图 3(a)所示,对柱式膜组件进行1:1三维建模,膜组件底部为气体进口,膜组件底部侧面为液体进口,膜组件顶部为出口,膜组件中间膜丝填充区域设置为多孔介质区域。中空纤维膜丝为聚偏氟乙烯材质,内外径分别为0.7 mm和1.3 mm,膜丝孔径为0.03 μm,组件膜丝填充率约为0.7。如图 3(b)所示,采用六面体结构网格对膜组件各部分进行网格划分。
|
图 3 柱式膜组件 Fig.3 Scheme of the column type membrane module |
欧拉模型能够模拟多相流,且欧拉模型用于模型中的每一相,采用了形式统一的模型方程, 计算相对简单且计算量较小,能大量节约计算时间及计算资源[12]。因此,采用欧拉模型作为多相流模型进行相关的计算模拟。在实验中观察发现膜组件曝气过程为湍流过程,因此在计算模拟时,设定膜组件内部为湍流。在两相流中,相间的作用力包括:曳力、升力、虚拟质量力、湍流扩散力以及壁面润滑力。在本文中只考虑曳力,曳力采用Schiller & Naumann模型[13],升力主要是以单个气泡为研究对象,在湍流等复杂流动中升力还有待进一步研究,其他几个力对两相流动影响较小,同时为了节约计算资源,故在此忽略不考虑[14~17]。
为了简化计算,本文对所模拟的体系做出如下几点假设:1.连续相和分散相均为不可压缩流体;2.两种流体遵循各自的控制方程;3.两种流体间无质量传递,等温流动;4.组件壳体内膜丝均匀分布,膜束视为一个整体的多孔介质。
3.2.1 守恒方程与多孔介质惯性阻力系数计算将膜束视为一个整体多孔介质,则多孔介质产生的阻力损失通过多孔介质模型表达,因此,在动量守恒方程右侧增加一个动量源项Sri从而引入多孔介质模型。连续性方程(1)和动量守恒方程(2)可以表达为如下形式:
| $\frac{\partial }{{\partial t}}\left( {{\alpha _i}{\rho _i}} \right) + \nabla \cdot \left( {{\alpha _i}{\rho _i}{{\bf{U}}_i}} \right) = 0$ | (1) |
| $\frac{\partial }{{\partial t}}\left( {{\alpha _i}{\rho _i}{\mathit{\boldsymbol{U}}_i}} \right){\rm{ + }}\nabla \cdot \left( {{\alpha _i}{\rho _i}{\mathit{\boldsymbol{U}}_i}{\mathit{\boldsymbol{U}}_i}} \right) = - {\alpha _i}\nabla p - \nabla \cdot \left( {{\alpha _i}{\tau _i}} \right) + {\mathit{\boldsymbol{F}}_i} + {S_{ri}} + {\alpha _i}{\rho _i}g$ | (2) |
方程中τi(i=l,g分别表示液相和气相)表示应力张量,U表示相的速度,α表示相的体积分数,Fi表示相间作用力,其表达式如下所示:
| ${F_i} = {F_{\rm{D}}} + {F_{\rm{L}}}{\rm{ + }}{F_{\rm{V}}} + {F_{\rm{T}}} + {F_{\rm{W}}}$ | (3) |
上式中,FD为曳力,FL为升力,FV为虚拟质量力,FT为湍流扩散力,FW为壁面润滑力(单位N⋅m-3)。
Sri表示动量源项,其表达式如下所示:
| ${S_{ri}} = - \left( {\sum\limits_{j = 1}^3 {{D_{ij}}\mu {v_j}} + \sum\limits_{j = 1}^3 {{C_{ij}}\frac{1}{2}\rho {v_{{\rm{mag}}}}{v_j}} } \right)$ | (4) |
| $D = \frac{1}{{{K_{{\rm{perm}}}}}}$ | (5) |
| $C = {K_{{\rm{loss}}}}$ | (6) |
μ表示动力学黏度,vmag表示表观速度大小,i=(1, 2, 3)表示不同的方向,Kperm表示渗透率,Kloss表示摩擦系数,方程式(4)中右侧第一项表示粘性阻力损失项,第二项表示惯性阻力损失项。膜组件在曝气过程中没有过滤,可以将中空纤维膜束视为无渗透行为的管束,因此,可以将上式(4)简化为:
| $\frac{{\Delta P}}{L} = - \sum\limits_{j = 1}^3 {K_{{\rm{loss}}}^j} \frac{1}{2}\rho {v_{{\rm{mag}}}}{v_j}$ | (7) |
惯性阻力系数Kloss为雷诺数的函数,同时受到膜组件的填充密度与水力直径数值的影响。
当流体方向与中空纤维膜组件的方向平行时,膜组件单位长度的压降可以表示为[18]:
| $\frac{{\Delta P}}{L} = - 1.98R{e^{ - 0.51}}D_{\rm{H}}^{ - 1.53} \cdot \frac{1}{2}\rho {u^2}$ | (8) |
当流体方向与中空纤维膜组件的方向垂直时,膜组件单位长度的压降可以表示为[18]:
| $\frac{{\Delta P}}{L} = - 13.5{\left( {\frac{{A\sqrt \mu }}{{V\sqrt u }}} \right)^{0.905}} \cdot \frac{1}{2}\rho {u^2}$ | (9) |
DH表示膜组件的水力直径,A表示膜的总面积,V表示膜组件中空隙体积之和,μ表示液相的黏度。
因此,根据方程(7)、(8)以及(9)得出当流动方向与中空纤维膜组件的方向分别为平行与垂直时,惯性阻力系数Kloss的计算表达式为:
| ${K_{{\rm{loss}}}}{\rm{ = }}1.98R{e^{ - 0.51}}D_{\rm{H}}^{ - 1.53}$ | (10) |
| ${K_{{\rm{loss}}}}{\rm{ = 13}}{\rm{.5}}{\left( {\frac{{A\sqrt \mu }}{{V\sqrt u }}} \right)^{0.905}}$ | (11) |
本数值模拟为非稳态计算模拟,时间步长取0.002 s,压力速度耦合采用Phase Couple SIMPLE算法,采用二阶迎风格式对湍动能与湍流耗散率进行离散化处理,残差精度取10-5。RNG k-ε模型和标准k-ε模型相似,但能够更好地处理高应变率及流线弯曲程度较大的流动,在计算收敛难易程度与计算所占用的资源方面,RNG k-ε模型较realizable k-ε模型具有更大的优势[12]。因此,采用RNG k-ε模型对动量方程进行封闭。
进口采用速度进口边界条件,出口采用压力出口边界条件。
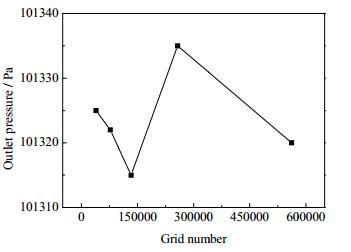
4 结果与讨论 4.1 网格无关性验证对于非稳态的模拟计算,需要验证网格数目与计算结果的相关性,即网格无关性验证。采用了5套不同的网格划分方案对模型进行网格划分,网格数量分别为561756,257259,132996,77136,39043。考察在相同曝气量条件(3 m3⋅h-1)下,组件的出口压力和网格质量系数(Equisize skew)在不同网格数下是否存在明显差异。
由图 4可知,网格数量从561756减少到39043的过程中,在相同的曝气量条件(3 m3⋅h-1)下,膜组件的出口压力变化的范围在10%以内;网格质量系数(Equisize skew)随网格数目的变化范围在6%以内,从以上计算结果可知,此时网格数量对计算结果影响很小。可以得出结论:网格数量在561756到39043范围内,可以认为39043网格数已经达到网格无关性,故取39042作为计算网格数。
|
图 4 网格数对组件出口压力的影响 Fig.4 Effects of grid number on pressure loss of the membrane module |
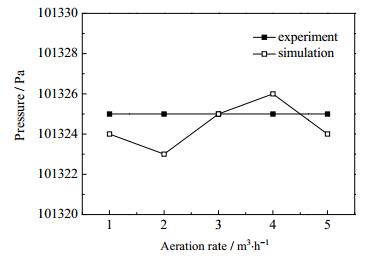
根据以上建立的6曝气孔柱式膜组件模型,计算模拟出6曝气孔膜组件在1~5 m3⋅h-1曝气量范围内膜组件出口压力,计算模拟结果与实验结果进行比较,以确定计算模拟准确性。
如图 5所示,计算模拟出膜组件出口压力随曝气量的增加始终在实验测量值的上下浮动。对比计算模拟的进出口压力与实验测量的数值,相对误差在10%以内,在可以接受的相对误差范围之内。说明本文所建立的模型与计算方法具有良好可靠性和准确性,在可接受的误差范围内能够准确地计算出膜组件出口压力。
|
图 5 模拟与实验对比图 Fig.5 Comparison of simulation and experimental results |
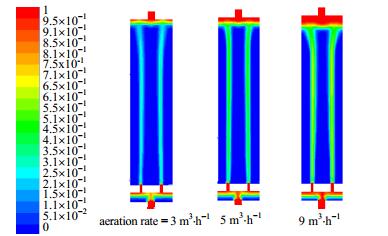
在气擦洗过程中,对膜面滤饼层等污染物地擦洗主要通过气液两相流中气泡经过膜面时所产生的壁面切应力的作用。因此,气相分布越均匀,越有利于膜组件内膜面地擦洗,从而减缓膜污染。在实际的膜组件曝气实验中发现当曝气时间达到8 s左右时,气液两相的分布达到一个较稳定的状态,因此,选择曝气时间为10 s时的计算模拟数据作为比较对象。
如图 6所示,膜组件的整体气含率随着曝气量的增加而增加,在膜组件的顶部区域的气相体积随着曝气量的增加而增加,但是,气相主要分布在曝气管的垂直上方位置,径向分布极不均匀。主要原因在于膜组件内部竖直填充的膜丝在轴向的阻力远小于在径向的阻力,其次,较少的曝气孔分布容易形成这样的射流现象。因此,对6曝气孔的膜组件的分布器需要进行优化设计,使膜组件在相同的曝气条件下气液分布更加均匀。
|
图 6 6曝气孔膜组件曝气量对气液分布的影响 Fig.6 Effects of aeration rates on gas-liquid distribution in the 6 aerator hole membrane module |
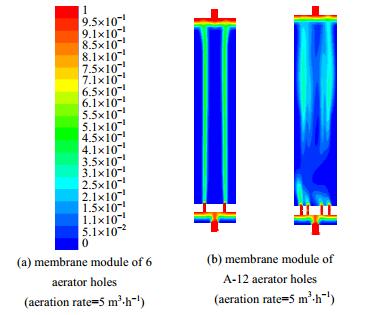
在曝气过程中,通过膜组件的分布器使气液两相流均匀分布在膜组件膜丝填充区域,以达到对膜丝较好的气擦洗效果。
如图 7所示,在相同曝气量(5 m3⋅h-1)条件下,A-12型膜组件在径向区域的气液分布均匀性优于6曝气孔膜组件,而且气相呈现摆动的上升趋势,有利于膜丝抖动脱除表面的污染物。在相同的操作条件下,增加曝气孔数量则产生的气泡更多,提高了气液两相的相互作用面。因此,气液两相在膜组件内部更加分布均匀。Zhang等[19]同样通过增加分布器的开孔率(增加开孔数目)来提高两相分布的均匀性。
|
图 7 曝气孔数目对气液流场分布的影响 Fig.7 Effects of aerator hole number on gas-liquid distribution |
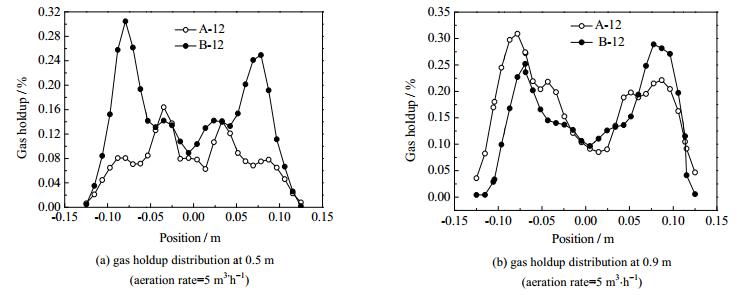
调整曝气孔的相对位置能够使气液两相从不同的初始位置进入到膜组件膜丝填充区域,促进两相之间相互作用,有利于气液两相均匀分布。
轴向高度为0.5 m时,组件内部气液两相沿径向的分布,如图 8(a)所示,在相同曝气量(5 m3⋅h-1)条件下,B-12型膜组件内部气液两相沿径向的分布均匀性优于A-12型膜组件。这说明曝气孔均匀分布有利于促进了膜组件内气液两相在径向区域的均匀分布,尤其是在膜组件轴向高度较低的区域。轴向高度为0.9 m时,组件内部气液两相沿径向的分布,如图 8(b)所示,在相同曝气量(5 m3⋅h-1)条件下,A-12型膜组件内部气液两相沿径向的分布均匀性与B-12膜组件基本一致。这说明沿着膜组件的轴向位置上升之后,A-12型膜组件内部气液两相在径向分布均匀性得到了较大的提高。主要原因在于,随着曝气的持续进行,气泡在上升过程中与液体以及膜丝之间的相互作用频率逐渐提高,气液两相在径向的均匀分布也得到了有效提高。此外,膜丝的抖动也能够有效地提高气液两相在径向的均匀分布。
|
图 8 曝气孔位置对气液流场分布的影响 Fig.8 Effects of aerator hole location on gas-liquid distribution |
在计算流体力学中湍流黏度并非流体的一个物理性质,表征速度脉动的一个特征值,反映的是旋涡活动的强烈程度,取决于流动状态。在气擦洗过程中适当提高膜面流体的湍流黏度,有利于提高两相流的速度脉动,从而有利于控制膜面污染与浓差极化程度。
如图 9所示,随着曝气量的增加组件内部区域的湍流黏度呈现先增加后减小最后到达一个平衡值。当曝气量在0~5 m3⋅h-1时,增加曝气量能够提高流场的湍流黏度,即提高流场速度脉动与旋涡活动强度;当曝气6~10 m3⋅h-1时,增加曝气量抑制了流场的湍流黏度的增加,即抑制流场的速度脉动与旋涡活动强度。主要原因在于,当曝气量较小时,膜组件内部压力相对较小,随着曝气量的增加,曝气促进了旋涡活动与速度脉动。但是随着曝气量的继续增加时,膜组件内部压力增加趋势大于两相流动速度脉动增加趋势,此时,膜组件内较大的压力抑制旋涡活动与速度脉动。因此膜组件采用5 m3⋅h-1的曝气量较为合理。
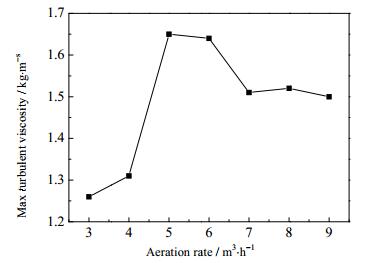
|
图 9 6曝气孔组件曝气量对湍流粘度的影响 Fig.9 Effects of aeration rates on turbulence viscosity of the 6 aerator hole membrane module |
湍流黏度的本质是涡流扩散,涡流扩散是湍流流体中的物质传递主要方式,那么湍流黏度的大小与分布特性能够直接反映出湍流中物质的传递效果。
如图 10所示,相比于6曝气孔组件,A-12曝气孔组件内部湍流黏度的均匀分布性更好。当曝气量为5 m3⋅h-1时,A-12型膜组件内部的湍流黏度就达到了较好的均匀分布效果,从而在较小的曝气量条件下就能够对膜丝进行均匀的气擦洗。主要是因为增加曝气孔的数量,提高了气液两相相互作用与两相均匀流动,从而有效促进膜组件内部湍流黏度地均匀分布。
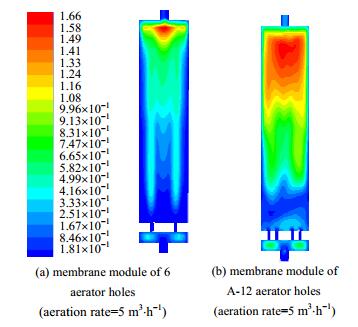
|
图 10 曝气孔数目对湍流黏度的影响 Fig.10 Effects of aerator hole number on turbulence viscosity |
湍流黏度分布的越均匀越有利于减缓膜污染。考察了曝气孔相对位置对湍流黏度分布的影响。
如图 11(a)、(b)所示,在相同的曝气孔数目与不同相对位置条件下,膜组件轴向区域的湍流黏度强度与均匀性得到进一步提高。通过调节曝气孔的相对位置,改变了气液两相流之间相互作用的角度,有利于提高湍流黏度的强度与均匀分布,从而有利于提高膜组件气擦洗清洗效果。因此,在相同的曝气过程中,B-12型膜组件具有更好的清洗效果。
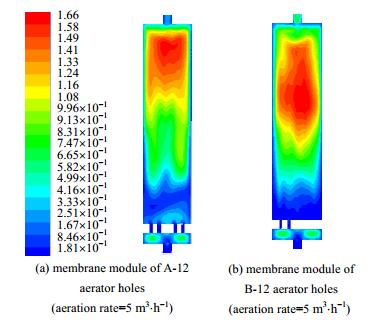
|
图 11 曝气孔相对位置对湍流黏度的影响 Fig.11 Effects of aerator hole location on turbulence viscosity |
在气液两相流中,液相速度是表征气液两相流中流体力学特性的基本参数,它直接影响到气体滞留程度、气液的混合程度等[20]。
如图 12所示,组件内的液体速度随曝气量的增大而增大,同时在膜丝填充区域形成循环流动。在曝气量从3 m3⋅h-1增加到9 m3⋅h-1的过程中,虽然膜丝填充区域液体的流速不断增加且形成循环流动,但是高速流动的液体主要分布在曝气孔上方。因此,在曝气过程中,较少的曝气孔数目不利于膜丝表面的气擦洗过程。
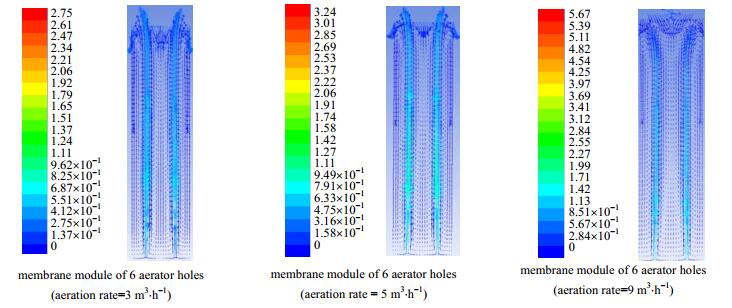
|
图 12 曝气量对液体速度的影响 Fig.12 Effects of aeration rates on liquid velocity |
对于利用气液两相流来对膜组件膜丝进行清洗,流体速度分布均匀或者形成摆动形式的流动有利于膜丝清洗。
如图 13所示,在相同的曝气量(5 m3⋅h-1)条件下,当曝气孔数目增加至12个时,膜组件内部液体流动由均匀对称的内循环流动过渡到液体摆动上升与内循环并存的流动形式。液体摆动上升有利于膜丝通过抖动脱除膜丝表面污染物,膜组件内部循环流动有利于增加气泡在组件内部的停留时间。

|
图 13 曝气孔数目对液体速度的影响 Fig.13 Effects of aerator hole number on liquid velocity |
如图 14所示,改变曝气孔相对位置并不会改变液体速度大小,只会改变液体速度在轴向和径向的分布。通过优化组件曝气孔相对位置,使得在曝气过程中,气液在的相互作用更加均匀,促进内部循环与涡流的形成。
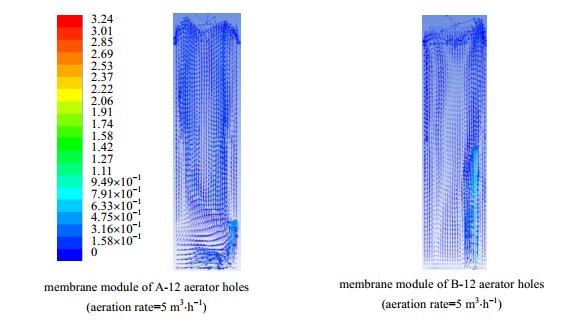
|
图 14 曝气孔相对位置对液体速度的影响 Fig.14 Effects of aerator hole location on liquid velocity |
(1) 采用CFD模拟软件,对带有6个曝气孔的柱式膜组件曝气过程进行了计算模拟,定量地计算出膜组件出口压力,模拟计算值与实验值吻合良好。
(2) 对带有6个曝气孔和不同构型的12个曝气孔的柱式膜组件曝气过程进行了计算模拟,研究表明:在曝气过程中,曝气量达到5 m3⋅h-1时,湍流黏度不再增加,曝气清洗采用5 m3⋅h-1较为合理;增加曝气孔数目、优化曝气孔相对位置能够有效提高气液两相以及湍流黏度在膜组件内部均匀分布,同时,在膜组件内部形成较多的涡流与循环流动,有利于膜丝的清洗。
(3) CFD模拟软件可以用于面向应用过程开发设计出流体力学性能优良的不同尺寸的膜组件,同时能够降低膜组件的设计开发成本。
符号说明:
| [1] | YANG Zhao(杨钊), CHENG Jing-cai(程景才), YANG Chao(杨超). Study on permeability of asymmetric ceramic membrane tubes with CFD simulation(非对称陶瓷膜孔渗透性能的CFD模拟研究)[J]. Journal of Chemical Industry and Engineering(化工学报) , 2015, 66(2): 3120-3129. |
| [2] | LIU Yang(刘洋), XU Zheng-liang(许振良), MA Xiao-hua(马晓华). Distillation performance of using PVA/PAN hollow fiber composite membrane as packing to separate the ethanol-water solution(中空纤维PVA/PAN复合膜填料的乙醇水溶液精馏性能)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报) , 2012, 26(2): 183-188. |
| [3] | YE Xiang-qun(叶向群), SUN Liang(孙亮), ZHANG Lin(张林), et al. CO2 removal from air by hollow-fiber membrane-based absorption system(中空纤维膜基吸收法脱除空气中二氧化碳的研究)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报) , 2003, 17(3): 237-242. |
| [4] | Shirazi M M A, Kargari A, Ismail A F. Computational fluid dynamic (CFD) opportunities applied to the membrane distillation process:state of the art and perspectives[J]. Desalination , 2016, 377: 73-90. DOI:10.1016/j.desal.2015.09.010. |
| [5] | Kaya R, Deveci G, Turken T. Analysis of wall shear stress on the outside-in type hollow fiber membrane modules by CFD simulation[J]. Desalination , 2014, 351: 109-119. DOI:10.1016/j.desal.2014.07.033. |
| [6] | YANG Yi(杨毅), WANG Bao-guo(王保国). Numerical simulation of shell-side flow in the hollow fiber membrane modules(中空纤维膜组件壳程流动的数值模拟)[J]. Journal of Chemical Industry and Engineering(化工学报) , 2008, 59(8): 1979-1985. |
| [7] | Bueiehorn S, Volmering D, Vossenkaul K. CFD simulation of single and multi-phase flows through submerged membrane units with irregular fiber arrangement[J]. Journal of Membrane Science , 2011, 384: 184-197. DOI:10.1016/j.memsci.2011.09.022. |
| [8] | Cai J J, Hawboldt K. Analysis of the effect of module design on gas absorption in cross flow hollow membrane contactors via computational fluid dynamics (CFD) analysis[J]. Journal of Membrane Science , 2016, 520: 415-424. DOI:10.1016/j.memsci.2016.07.054. |
| [9] | PENG Wen-bo(彭文博), QI Hong(漆虹), CHEN Gang-lin(陈纲领), et al. CFD modeling of permeate process in 19-channelporous ceramic membranes(19通道多孔陶瓷膜渗透过程的CFD模拟)[J]. Journal of Chemical Industry and Engineering(化工学报) , 2007, 58(8): 2021-2026. |
| [10] | PENG Wen-bo(彭文博), QI Hong(漆虹), LI Wei-xing(李卫星), et al. Experimental investigation of effects of ceramic membranechannels on flux and optimization with CFD(陶瓷膜通道相互作用的实验分析及CFD优化)[J]. Journal of Chemical Industry and Engineering(化工学报) , 2008, 59(3): 602-606. |
| [11] | ZOU Lin-lin(邹琳玲), QI Hong(漆虹), XING Wei-hong(邢卫红). Membrane thickness gradient of isoflux ceramic membrane based on CFD(基于CFD的恒通量陶瓷膜厚度设计)[J]. Journal of Chemical Industry and Engineering(化工学报) , 2010, 61(10): 2615-2619. |
| [12] | WANG Fu-jun(王福军). Computational fluid dynamics(计算流体力学分析)[M].Beijing(北京): Tsinghua University Press(清华大学出版社), 2004. |
| [13] | LI Guang(李光), YANG Xiao-guang(杨晓光), DAI Gan-ce(戴干策). Numerical modelling of bubbling flow dynamic behaviourina bubblecolum(鼓泡塔反应器气液两相流CFD数值模拟)[J]. Journal of Chemical Industry and Engineering(化工学报) , 2008, 59(8): 1858-1965. |
| [14] | Hatasgu K, Tomiyama A. A drag correlation of fluid particles rising through stagnant liquids in vertical pipes at intermediate reynolds numbers[J]. Chemical Engineering Sciecce , 2009, 64(12): 3019-3028. DOI:10.1016/j.ces.2009.03.013. |
| [15] | Hazi G, Mayer G, Markus A. Drag force acting on bubbles in a subchannel of triangular array of rods[J]. International Journalof Heat and Mass Transfer , 2009, 52: 1481-1487. DOI:10.1016/j.ijheatmasstransfer.2008.09.005. |
| [16] | Lucas D, Tomiyama A. On the role of the lateral lift force in poly-dispersed bubbly flows[J]. International Journal Multiphas Flow , 2011, 37(9): 1178-1190. DOI:10.1016/j.ijmultiphaseflow.2011.05.009. |
| [17] | Zhang D, Deen N G, Kuipers J A M. Numerical simulation of the dynamic flow behavior in a bubble column:A study of closures for turbulence and interface forces[J]. Chemical Engineering Sciecce , 2006, 61(23): 7593-7608. DOI:10.1016/j.ces.2006.08.053. |
| [18] | LIU Xue-fei, WANG Yuan. Numerical simulations of impact of membrane module design variables on aerationpatterns in membrane bioreactors[J]. Journal of Membrane Science , 2016, 520: 201-213. DOI:10.1016/j.memsci.2016.07.011. |
| [19] | Zhang F, Zhang Z H, L Y F, et al. Effect of gas distributor on hydrodynamics and the rochow reaction in a fluidized bed membrane reactor[J]. Industrial & Engineering Chemistry Research , 2017, 55(40): 10600-10608. |
| [20] | LUO Xiao(罗潇), LIU Ping-le(刘平乐). Modeling of liquid circulation in gas-liquid bubble columns(气液鼓泡床内的液体流速分布)[J]. Journal of Chemical Industry and Engineering(化工学报) , 2006, 57(7): 1565-1569. |




