固体悬浮操作在化工、冶金、食品和制药等过程工业中很常见。借助搅拌器的作用,将固体颗粒分散到液相,增大固-液两相间的接触面积,从而加快反应速率、提高传质效率、强化传热过程,因此,搅拌器的固相悬浮性能直接影响搅拌槽内的混合效率[1]。固-液搅拌操作通常采用轴流式搅拌器[2],推进式搅拌器是典型的轴流式搅拌器,循环性能好、动力消耗低,在较低的搅拌功率下便可获得较好的固相悬浮效果[3]。
目前,已有大量学者对固-液两相体系下推进式搅拌器的固相悬浮性能进行了研究。赖家凤等[4]对体积固含率φV=10% 的消防砂-清水两相体系,通过实验研究了推进式搅拌器的搅拌流型,发现在无挡板工况下,当搅拌物料较少或搅拌转速较高时,容易在搅拌轴中心区域形成漩涡。Yamazaki等[5]研究了推进式搅拌器在φV =15%的玻璃微珠/石英砂-清水两相体系中达到临界离底悬浮状态时的固相浓度分布状况,随着轴向高度的增加,液面附近的固相浓度明显降低,而在不同径向位置的轴向浓度分布状况非常一致,说明在径向方向上的浓度分布较为均匀。钟天铖等[3]采用数值模拟方法获得了在推进式搅拌器作用下清水体系的速度分布、搅拌力矩与功率数值,结果表明,流体在推进式搅拌器作用下能产生较大的轴向速度,主体循环效果明显。此外,推进式搅拌器受到的剪切力矩较小,适用于高速旋转工况,并能以较低的功率消耗获得大流量、强循环的搅拌效果。Pour等[6]利用CFD模型对比研究了直六叶桨和推进式搅拌桨作用下φV =5%的固-液两相体系的流场以及固相浓度分布,二者产生的流场不同,但在径向方向上的分布状况却颇为相似;对比二者在轴向方向上的浓度分布情况,发现推进式搅拌桨更适用于低速或高速运转的固-液悬浮体系。
一般认为,体积固含率大于20%的体系为高固稠密体系,低于20%的则为低固稀薄体系[7-8]。前人已经通过实验和模拟方法对推进式搅拌器的固相悬浮性能展开了研究,但以往研究多集中于低固稀薄体系,且大多选择清水作为液相[9-10]。事实上,在工业生产中,高固稠密体系更为常见,如矿物冶炼领域的矿浆搅拌过程[11],这是因为提高固含率有利于提高生产效率。同时在高固稠密体系搅拌中,优化固含率可以有效降低能耗、减少污染。考虑到推进式搅拌器在固-液搅拌操作中的广泛应用,有必要探究其在宽固含率范围内对固相悬浮性能的影响,为工业上选择合适的悬浮液操作浓度提供指导。
因此,本研究采用实验研究方法,在φV为3%~30%条件下,考察搅拌结构参数(桨叶直径、桨叶离底高度)和物料物性(固相粒径、液相黏度) 等因素对推进式搅拌器的固相悬浮性能的影响,并尝试建立一个适用于推进式搅拌器单位质量搅拌功率的预测公式。
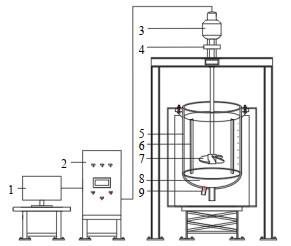
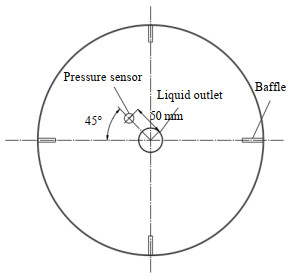
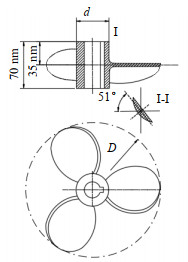
2 实验部分 2.1 实验装置及物料实验装置如图 1、2所示,搅拌釜5为圆柱形的有机玻璃釜,搅拌釜直径T以及静止状态下的液位高度H均为380 mm,即高径比H/T=1.0。此液位下的总体积约为43.1 L。搅拌釜内壁均布四块全深度挡板6,挡板宽度为38 mm、厚度为10 mm。所用搅拌器为标准的三叶推进式搅拌器,搅拌桨叶7的结构如图 3所示,选用的桨叶直径为135和200 mm两种,采用下压模式运行。釜底下方为椭圆形空腔8,为了避免固相与压力传感器之间的直接接触对压力值测量产生影响,釜底压力通过装有滤网的底部小孔传递至空腔内,再由安装在空腔底部的压力传感器9进行测量。底部小孔的直径为5 mm,到釜底中心的距离为80 mm。
|
图 1 搅拌实验台 Fig.1 Schematic diagram of the stirring setup 1.computer 2 platform 3.motor 4. torque sensor 5. stirred tank 6.baffle 7.impellor 8.oval cavity 9.pressure sensor |
|
图 2 搅拌釜俯视图 Fig.2 Vertical view of the stirred tank |
|
图 3 搅拌器结构图 Fig.3 Schematic diagram of the agitator structure |
实验选用食品级麦芽糖浆为原料,与清水以两种不同比例混合获得糖浆水溶液,两种糖浆溶液的黏度和密度如表 1所示。选用玻璃微珠为固相,其密度为2 500 kg·m-3,粒径为440、630、1 013 μm三种。
|
|
表 1 糖浆物性 Table 1 Physical properties of syrup |
实验测量的参数主要包括搅拌功率和临界离底悬浮转速。为了提高测量结果的准确性,所有工况下的实验数据均重复测量3~5次,保证相对误差在5%以内,并以标准偏差作为误差棒来表示测量数据的不确定度。同时,基于实验数据建立拟合曲线,并用确定系数R2评价曲线的偏差情况。
2.2.1 搅拌功率的测量搅拌功率的测量方法采用扭矩法。由于阻力损失无法避免,实际搅拌扭矩为负载扭矩M负载减去空载扭矩M空载,再根据式(1)、(2)分别计算搅拌功率P和单位体积搅拌功率PV。
| $ P=2\pi N\left({M}_{负载}-{M}_{空载}\right)$ | (1) |
| ${P_V} = P/V$ | (2) |
达到临界离底悬浮状态时,单位质量固相悬浮所消耗的功率被定义为单位质量搅拌功率εjs[10],其计算式如下:
| $ {\epsilon }_{\rm{js}}=\frac{{P}_{\rm{js}}}{{M}_{\rm{s}}}=\frac{2\pi {N}_{\rm{js}}\left({M}_{负载}-{M}_{空载}\right)}{{M}_{\rm{s}}}$ | (3) |
其中,固相总质量Ms计算式如下:
| ${M_{\rm{s}}} = V{\varphi _V}{\rho _{\rm{s}}}$ | (4) |
临界离底悬浮转速Njs的测量采用压力法,根据釜底静压与被悬起的固相质量之间的关系来确定Njs[12]。釜底总压差Δp包括静压差Δpstatic和动压差Δpdynamic,Micale等[12]研究表明,釜底总压差Δp与搅拌转速N的关系可表示如下:
| $\Delta p = \Delta {p_{{\rm{static}}}}{\rm{ + }}\Delta {p_{{\rm{dynamic}}}}{\rm{ = }}\frac{{{{M'}_{\rm{s}}}\left( {1 - \frac{{{\rho _L}}}{{{\rho _{\rm{s}}}}}} \right)g{\rm{ }}}}{A}{\rm{ + }}a{N^2}$ | (5) |
达到临界离底悬浮状态后,静压差达到最大值且不再随搅拌转速变化,此时Δp与N的关系可表示如下:
| $\Delta p = \Delta {p_{{\rm{js}}}}{\rm{ + }}\Delta {p_{{\rm{dynamic}}}}{\rm{ = }}\frac{{{M_{\rm{s}}}\left( {1 - \frac{{{\rho _L}}}{{{\rho _{\rm{s}}}}}} \right)g{\rm{ }}}}{A}{\rm{ + }}a{N^2}$ | (6) |
安装并校准压力传感器后,记录静止状态下的釜底初始压力值;启动搅拌器,从0开始增加搅拌转速,每次增加50 r·min-1,待压力传感器示数稳定后,借助数据采集软件记录该转速下的釜底压力值。观察釜内固相悬浮状态,接近均匀悬浮时停止增加转速,获得固-液两相体系下的Δp~N关系曲线;再根据式(5)计算每一个转速对应的动压差值,获得
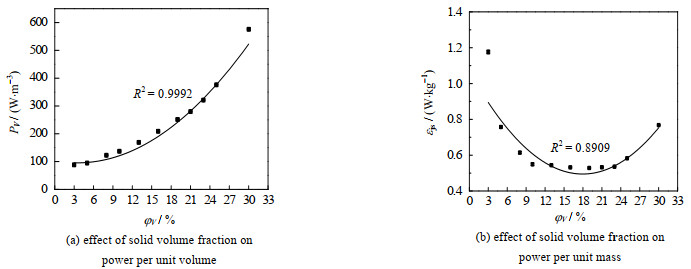
图 4(a)为推进式搅拌器在临界离底悬浮状态下的单位体积搅拌功率PV随体积固含率φV的变化曲线。由图可见,当φV低于10%时,随着φV增大,PV增长缓慢,曲线斜率最大约为7.04;当φV为10%~20%时,曲线斜率平均约为12.65,PV增大速率有所变大;当φV超过20% 以后,曲线斜率达到20以上,PV呈现指数增长趋势。此结果与Bubbico等[13]的研究结果相符,该研究采用砂子-水高固稠密体系,也发现在固含率超过一定数值后,PV会急剧增加。这是由于在较高固含率下,固-液间摩擦、颗粒-颗粒间碰撞和颗粒-设备间碰撞难以忽视,引起的能量耗散需要更多额外的能量来补偿。
|
图 4 体积固含率对搅拌功率的影响 Fig.4 Effects of solid volume fraction on stirring power (D = 0.35T, h = T/4, with baffle, dp = 440 μm, μ = 15 mPas) |
图 4(b)为推进式搅拌器单位质量搅拌功率εjs随φV的变化曲线,由图可见,εjs先随φV增大而降低,当φV约为20%时达到临界值,随后增大。此外,由图还可见,φV =3% 的悬浮液εjs值约为25% 的悬浮液的两倍,而φV =8%的悬浮液εjs值与25% 的悬浮液几乎相等。这是由于当固含率较低时,通过旋转的桨叶传输到釜内的大部分能量被用于推动液体流动而不是使固相悬浮,导致搅拌设备使用不足从而增加运营成本,降低了能量利用率;随着固含率的增加,越来越多的能量被用于固相的悬浮,当达到最优值时,传输到釜内的能量恰好足以推动所有的液体并悬浮所有固相。一旦固含率超过最优值,釜内具有较少的液体和较多的固相,固相悬浮较为困难,能量耗散较大,于是整个搅拌釜的能量利用率降低[14-16]。因此,εjs~φV曲线呈现先减小后增大的“U”形。综上分析可知,搅拌器的能量利用率有可能存在最优值,因此,Wu等[7]提出了最优固含率的概念,即在最优固含率φvop下,使单位质量固相悬浮所需要的功率最低。明确不同参数对最优固含率的影响规律,从而合理地选择悬浮液操作浓度,对于提高搅拌器的生产率和能量利用率具有重要意义。
3.2 单位质量搅拌功率的影响因素 3.2.1 搅拌桨直径的影响图 5绘出了搅拌桨桨叶外径D分别为0.35T和0.53T的推进式搅拌器在不同固含率下的εjs曲线。由图可见,当φV低于10%时,两条曲线的差距较大,且小直径桨叶具有更低的εjs;当φV为10%~20% 时,二者十分接近;当φV超过20% 时,两者差距又变大,且小直径桨叶的εjs低于大直径桨叶。此外,从图中还可见,D为0.35T和0.53T的推进式搅拌器的φvop分别为20% 和17%,即随着搅拌桨直径增大,最优固含率略微减小。因此,在下面实验中D均采用0.35T。
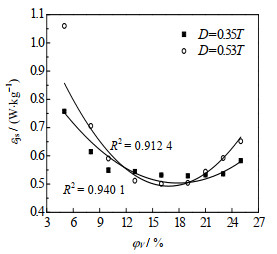
|
图 5 搅拌桨直径对单位质量搅拌功率的影响 Fig.5 Effects of blade diameter on power per unit mass (h = T/4, with baffle, φo = 21%, dp = 440 μm, μ = 15 mPa·s) |
观察推进式搅拌器桨叶在不同离底高度h下的εjs~φV曲线可知(见图 6),εjs随h增大而增大,这与Zwietering[17]和Nienow[18]的研究结果一致。这是因为,h越大,桨叶排出流距离釜底越远,对釜底的作用越弱,导致颗粒的悬浮越困难,需要消耗更多的能量。此外,由图 6还可见,不同h值对应的εjs~φV曲线变化趋势较为一致,h为T/3、T/4、T/5时对应的φvop分别为16%、20%、16%,这意味着φV对φvop的影响不明显。在下面实验中h均采用T/4。
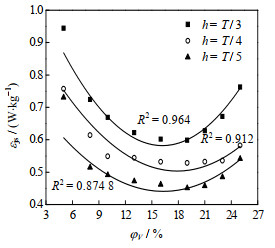
|
图 6 桨叶离底高度对单位质量搅拌功率的影响 Fig.6 Effects of off-bottom clearance on power per unit mass (D = 0.35T, with baffle, φo = 21%, dp = 440 μm, μ = 15 mPa·s) |
图 7为D=0.35T、h=T/4时推进式搅拌器在固相粒径分别为440、633和1 013 μm的固-液体系条件下,εjs随φV的变化曲线。由图可见,在相同的φV下,粒径为1 013 μm的εjs值约为633 μm的2倍、440 μm的4倍,即单位质量固相悬浮所消耗的功率与固相粒径呈正相关,这是因为颗粒粒径越大,其沉降速度越快,故需要更多的能量来产生更高的液相速度和更大程度的湍流强度才能实现固相的悬浮[19]。因此,对于相同质量的固相,悬浮数量较多的小颗粒比悬浮数量较少的大颗粒更节能。此外,由图还可见,粒径为1 013 μm的εjs~φV曲线近似为“U”形,其他两条曲线则较为平坦。这是因为,固含率的增加会使搅拌功率增加,同时粒径的增大也会使搅拌功率增加,在二者的综合作用下,当固含率的增幅相同时,与小粒径相比,大粒径的搅拌功率增幅会更大,从而导致εjs~φV曲线的变化幅度更大。
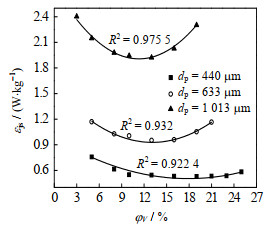
|
图 7 固相粒径对单位质量搅拌功率的影响 Fig.7 Effects of solid particle size on power per unit mass (D = 0.35T, h = T/4, with baffle, φo = 21%, μ = 15 mPa·s) |
进一步研究粒径对φvop的影响可以发现,粒径为1 013、633和440 μm的工况对应的φvop分别为12%、14%和20%,对应的单位质量搅拌功率分别为1.91、0.92和0.52 W·kg-1,这表明,粒径越小φvop值越大,这是因为,小粒径的悬浮性能更优,颗粒间的相互作用更弱,从而具有更低的能量损耗,φvop则随之变大。
3.2.4 液相黏度的影响为了探究液相黏度对推进式搅拌器单位质量搅拌功率的影响,绘制了清水体系(μ=1 mPa·s)以及黏度分别为15和50 mPa·s的黏性体系下εjs随φV的变化曲线,如图 8所示。对比这三条曲线可见,φV相同时,清水体系的εjs值约为黏度15 mPa·s体系的1.3倍、黏度50 mPa·s体系的1.7倍。这表明,εjs随体系黏度的增大而降低,这是由于固-液两相间的曳力随黏度增大而增大,颗粒的悬浮变得更容易,这与Wu等[20]的研究结果一致。由图还可见,清水体系以及黏度分别为15和50 mPa·s的黏性体系对应的φvop值分别为17%、20%和20%,对应的εjs分别为0.69、0.52和0.42 W·kg-1,显然可见,两个黏度体系相比,φvop值相同、εjs值随黏度增大而变小;而与黏度体系相比,增大相同程度的固含率,清水体系的εjs值明显变大,即需要输入更多的功率达到临界离底悬浮状态。
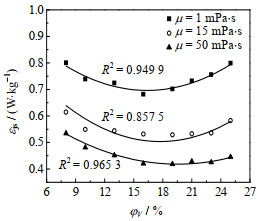
|
图 8 液相黏度对单位质量搅拌功率的影响 Fig.8 Effects of liquid viscosity on power per unit mass (D = 0.35T, h = T/4, with baffle, φo = 21%, dp = 440 μm) |
影响固相悬浮性能的因素多且复杂,难以通过理论推导方法获得相应结果[21]。为此,利用数据拟合方法对得到的实验数据进行分析及处理,获得εjs的预测公式,以便预测搅拌器在不同工况下的φvop值。
针对固-液两相体系的搅拌混合过程,Bubbico等[13]提出了临界离底悬浮状态下的搅拌功率Pjs与φV之间的经验关系式如下:
| ${P_{{\rm{js}}}} = \left( {1 + k{\varphi _V}} \right){N_{\rm{p}}}{\rho _{\rm{m}}}N_{{\rm{js}}}^3{D^5}$ | (7) |
式中:k为常数,代表因固相存在而引起的能量耗散的度量;Np为搅拌器的功率准数,其不仅与搅拌器的几何尺寸有关,还与被搅物料的物性有关;对于标准三叶推进式搅拌器而言,在本实验工况下,Np的数值约为0.35[20];ρm为悬浮液的密度,kg·m-3,其计算公式如下:
| ${\rho _{\rm{m}}} = {\rho _{\rm{s}}}{\varphi _V} + {\rho _L}\left( {{\rm{1}} - {\varphi _V}} \right)$ | (8) |
参照Zwietering[17]提出的关联式,可将临界离底悬浮转速Njs与各影响因素之间的关系表示为:
| ${N_{{\rm{js}}}} = S{\nu ^{{a_1}}}{d_{\rm{p}}}^{{a_2}}{\left( {\frac{{g\Delta \rho }}{{{\rho _{\rm{L}}}}}} \right)^{{a_3}}}{X^{{a_4}}}$ | (9) |
式中:S为与搅拌釜结构、桨叶类型等相关的常数;X为固液质量比,代表固含率的影响,其计算公式如下:
| $X = \frac{{{\rho _{\rm{s}}}{\varphi _V}}}{{{\rho _{\rm{L}}}\left( {1 - {\varphi _V}} \right)}}$ | (10) |
对各个工况下的Njs实验数据进行拟合,可得到Njs的预测公式为:
| ${N_{{\rm{js}}}} = {\rm{1}}{\rm{.122 8}} \times {\rm{1}}{{\rm{0}}^{\rm{6}}}{\nu ^{ - {\rm{1}}{\rm{.057 1}}}}{d_{\rm{p}}}^{{\rm{0}}{\rm{.466 75}}}{\left( {\frac{{g\Delta \rho }}{{{\rho _{\rm{L}}}}}} \right)^{ - {\rm{8}}{\rm{.473 68}}}}{X^{{\rm{0}}{\rm{.122}}}}$ | (11) |
此时,可将εjs表示为
| ${\varepsilon _{{\rm{js}}}} = {\rm{0}}{\rm{.35}}\left( {k + \frac{1}{{{\varphi _V}}}} \right)\frac{{{\rho _{\rm{m}}}}}{{V{\rho _{\rm{s}}}}}{\left[ {{\rm{1}}{\rm{.122 8}} \times {\rm{1}}{{\rm{0}}^{\rm{6}}}{\nu ^{ - {\rm{1}}{\rm{.057 1}}}}{d_{\mathop{\rm p}\nolimits} }^{{\rm{0}}{\rm{.466 75}}}{{\left( {\frac{{g\Delta \rho }}{{{\rho _L}}}} \right)}^{ - {\rm{8}}{\rm{.473 68}}}}{X^{{\rm{0}}{\rm{.122}}}}} \right]^3}{D^5}$ | (12) |
利用各个工况下εjs的实验数据对式(12) 进行拟合,可得到系数k = 6.4,即εjs的预测公式最终可表示为
| ${\varepsilon _{{\rm{js}}}} = {\rm{0}}{\rm{.35}} \times \left( {{\rm{6}}{\rm{.4}} + \frac{1}{{{\varphi _V}}}} \right)\frac{{\rho {}_{\rm{m}}}}{{V{\rho _{\rm{s}}}}}{\left[ {{\rm{1}}{\rm{.122 8}} \times {\rm{1}}{{\rm{0}}^{\rm{6}}}{\nu ^{ - {\rm{1}}{\rm{.057 1}}}}{d_{\rm{p}}}^{{\rm{0}}{\rm{.466 75}}}{{\left( {\frac{{g\Delta \rho }}{{{\rho _L}}}} \right)}^{ - {\rm{8}}{\rm{.473 68}}}}{X^{{\rm{0}}{\rm{.122}}}}} \right]^3}{D^5}$ | (13) |
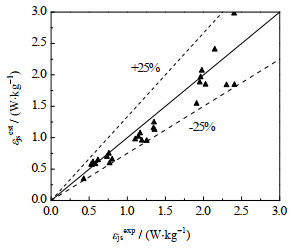
图 9为单位质量功率预测值与实验值对比图,由图可见,预测值与实验值的最大误差约为25%,拟合效果较好。此外,式(13) 的定义范围为液相密度1 000~1 261 kg·m-3、固相粒径440~1 013 μm、固相密度2 500 kg·m-3、体积固含率3%~30%,对于此范围之外的工况,该式的适用性有待进一步研究。
|
图 9 单位质量搅拌功率预测值与实验值对比 Fig.9 Comparison of predicted and experimental values of power per unit mass |
在液相黏度为15 mPa·s、液相密度为1 186 kg·m-3、固相粒径为440 μm、固相密度为2 500 kg·m-3的两相体系下,将对应的物性代入式(13)后,可将该工况下的εjs与φV之间的关系表示为
| ${\varepsilon _{{\rm{js}}}} = {\rm{0}}{\rm{.35}} \times \left( {{\rm{6}}{\rm{.4}} + \frac{1}{{{\varphi _V}}}} \right)\frac{{\left[ {2_{}^{}500{\varphi _V} + {1_{}}186\left( {1 - {\varphi _V}} \right)} \right]}}{{{2_{}}500 \times {\rm{0}}{\rm{.043}}}}{\left[ {{\rm{7}}{\rm{.156}} \times {{\left( {\frac{{{2_{}}500 \times {\varphi _V}}}{{{1_{}}186 \times \left( {1 - {\varphi _V}} \right)}}} \right)}^{{\rm{0}}{\rm{.122}}}}} \right]^3} \times {0.135^5}$ | (14) |
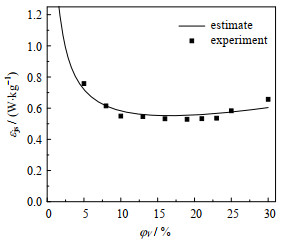
图 10为φV在0~30%连续变化时,由式(14)得到的εjs预测曲线。由图可见,εjs的预测值随φV的增大先迅速减小再缓慢增大,φvop约为19%,而实验测定该工况下的φvop为20%,这表明二者具有较好的一致性,即该预测公式能够较好地预测对应工况下εjs随φV变化规律以及φvop值。
|
图 10 单位质量搅拌功率预测曲线 Fig.10 Prediction curve of power per unit mass (D = 0.35T, h = T/4, with baffle, dp = 440 μm, μ = 15 mPa·s) |
本研究主要涉及推进式搅拌器在一系列固相浓度范围内的固相悬浮性能,考察了搅拌器的结构参数和物料物性对临界离底悬浮状态下的搅拌功率的影响。具体结论如下:
(1) 体积固含率由3% 增加到30% 过程中,达到临界离底悬浮状态时,推进式搅拌器的单位体积搅拌功率单调增加,而单位质量搅拌功率呈现出先减小后增加的“U”形,存在最优固含率,即具有最低单位质量搅拌功率;
(2) 搅拌器的结构参数对固相悬浮性能的影响:小直径桨叶的单位质量搅拌功率低于大桨叶的,具有更好的固相悬浮性能,其最优固含率略高于大桨叶;单位质量搅拌功率随离底高度增大而增大,最优固含率则基本不受离底高度的影响。因此,考虑到固液悬浮能耗问题,在固-液搅拌操作中,建议采用较小直径的搅拌桨和较小离底高度;
(3) 物性对固相悬浮性能的影响:固相粒径越小,颗粒间的相互作用力越弱,固相悬浮性能越优,从而具有更低的能量损耗,最优固含率也越大;黏性体系与清水体系相比,随着液相黏度增大固相悬浮更容易,单位质量搅拌功率更小,最优固含率更高。因此,在固-液搅拌操作中,应趋于选择较小粒径的固相以及黏性较大的体系;
(4) 在结构参数确定的前提下,考察了若干物性对单位质量搅拌功率的影响,提出了一个适用于三叶推进式搅拌器的单位质量搅拌功率预测公式。该公式能较好地预测物性对单位质量搅拌功率的影响,可得到不同工况下的最优固含率,为工业上固-液搅拌操作中选择合适的悬浮液操作浓度提供一定的指导。
符号说明:
|
|
| [1] |
OLDSHUE J Y. Mixing of solid-liquid suspensions[J]. Journal of Pharmaceutical Sciences, 2010, 50(6): 523-530. |
| [2] |
徐峰, 李龙, 程云山. 轴流式搅拌器的研究与发展[J]. 石油化工设备技术, 2004, 25(6): 27-30. XU F, LI L, CHENG Y S. Research and development of axial flow agitator[J]. Petrochemical Equipment Technology, 2004, 25(6): 27-30. DOI:10.3969/j.issn.1006-8805.2004.06.008 |
| [3] |
钟天铖, 汤文成, 刘碧茜, 等. 推进式搅拌器固液混合的计算流体力学模拟[J]. 东南大学学报(自然科学版), 2016, 46(4): 713-719. ZHONG T C, TANG W C, LIU B Q, et al. CFD simulation of solid-liquid mixing in a propeller agitator[J]. Journal of Southeast University (Natural Science), 2016, 46(4): 713-719. |
| [4] |
赖家凤, 郭政, 晁会霞, 等. 固液悬浮体系搅拌桨选型的实验研究[J]. 钦州学院学报, 2018, 33(5): 14-17. LAI J F, GUO Z, CHAO H X, et al. Experimental study on the selection of agitator for solid-liquid suspension system[J]. Journal of Qinzhou University, 2018, 33(5): 14-17. |
| [5] |
YAMAZAKI H, TOJO K, MIYANAMI K. Measurement of local solids concentration in a suspension by an optical method[J]. Powder Technology, 1992, 70(1): 93-96. DOI:10.1016/0032-5910(92)85059-5 |
| [6] |
POUR M H, NANSA V M, SABERI M, et al. CFD simulation of solid-liquid stirred tank with rushton turbine and propeller impeller[J]. International Journal of Chemical and Molecular Engineering, 2013, 7(6): 410-413. |
| [7] |
WU J, WANG S, GRAHAM L, et al. High solids concentration agitation for minerals process intensification[J]. AIChE Journal, 2011, 57(9): 2316-2324. DOI:10.1002/aic.12468 |
| [8] |
PAGLIANTI A, CARLETTI C, MONTANTE G. Liquid mixing time in dense solid-liquid stirred tanks[J]. Chemical Engineering & Technology, 2017, 40(5): 862-869. |
| [9] |
GRENVILLE R K, MAK A T C, BROWN D A R. Suspension of solid particles in vessels agitated by axial flow impellers[J]. Chemical Engineering Research & Design, 2015, 100: 282-291. |
| [10] |
GRENVILLE R K, GIACOMELLI J J, BROWN D A R. Suspension of solid particles in vessels agitated by rushton turbine imperllers[J]. Chemical Engineering Research & Design, 2016, 109: 730-733. |
| [11] |
李军, 刘新刚, 宋翔宇, 等. 某难选金矿综合回收试验研究[J]. 黄金, 2015, 36(10): 58-61. LI J, LIU X G, SONG X Y, et al. Experimental study on comprehensive recovery of a refractory gold deposit[J]. Gold, 2015, 36(10): 58-61. DOI:10.11792/hj201510013 |
| [12] |
MICALE G, GRISAFI F, BRUCATO A. Assessment of particle suspension conditions in stirred vessels by means of pressure gauge technique[J]. Chemical Engineering Research & Design, 2002, 80(8): 893-902. |
| [13] |
BUBBICO R, CAVE S D, MAZZAROTTA B. Agitation power for solid-liquid suspensions containing large particles[J]. The Canadian Journal of Chemical Engineering, 1998, 76(3): 428-432. DOI:10.1002/cjce.5450760312 |
| [14] |
DREWER G R, AHMED N, JAMESON G J. An optimum concentration for the suspension of solids in stirred vessels[J]. Mixing and Crystallization, 2000, 83-94. |
| [15] |
LU W M, WU H Z, JU M Y. Effects of baffle design on the liquid mixing in an aerated stirred tank with standard Rushton turbine impellers[J]. Chemical Engineering Science, 1997, 52(21-22): 3843-3851. DOI:10.1016/S0009-2509(97)88929-4 |
| [16] |
BRUCATO A, CIPOLLINA A, MICALE G, et al. Particle suspension in top-covered unbaffled tanks[J]. Chemical Engineering Science, 2010, 65(10): 3001-3008. DOI:10.1016/j.ces.2010.01.026 |
| [17] |
ZWIETERING T N. Suspending of solid particles in liquid by agitators[J]. Chemical Engineering Science, 1958, 8(3/4): 244-253. |
| [18] |
NIENOW A W. Suspension of solid particles in turbine agitated baffled vessels[J]. Chemical Engineering Science, 1968, 23(12): 1453-1459. DOI:10.1016/0009-2509(68)89055-4 |
| [19] |
LIU B Q, XU Z L, FAN F Y, et al. Experimental study on the solid suspension characteristics of coaxial mixers[J]. Chemical Engineering Research & Design, 2018, 133: 335-346. |
| [20] |
WU J, ZHU Y, PULLUM L. The effect of impeller pumping and fluid rheology on solids suspension in a stirred vessel[J]. Canadian Journal of Chemical Engineering, 2001, 79(2): 177-186. DOI:10.1002/cjce.5450790201 |
| [21] |
陈乙崇. 化工设备设计全书: 搅拌设备设计[M]. 上海: 上海科学技术出版社, 1985: 43-45. CHEN Y C. Chemical equipment design book: Mixing equipment design[M]. Shanghai: Shanghai Science and Technology Press, 1985: 43-45. |




