沸腾传热具有相对更高的传热效率,广泛应用于化工、电力、冶金等领域[1]。对沸腾传热开展准确的计算才能支撑各类换热设备的设计开发。核电非能动余热排出热交换器(passive residual heat removal heat exchanger,PRHR HX)为C型管结构,在事故运行工况下,管外冷却水在一回路冷却剂的作用下,会出现从自然对流、过冷沸腾到饱和沸腾的整个传热过程。其中,过冷沸腾为自然对流和饱和沸腾之间的过渡阶段,该阶段的传热特性对分析该类热交换器的性能及热工设计具有重要的影响[2-3]。
现有过冷沸腾传热计算公式大多针对不同工况、不同结构,通过实验或模拟的方法得到,主要集中在有限空间内强制流动过冷沸腾及有限空间内自然循环过冷沸腾,而对于池内异型管外过冷沸腾的研究较为少见,且现有模型及公式在适用范围上均有很大限制。当前用于计算过冷沸腾的模型主要有
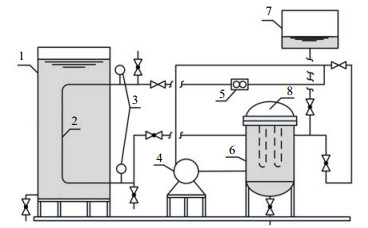
图 1为单管传热实验装置工艺流程图。实验装置由C型换热管、水箱、导热油罐、电加热器、离心泵、流量计、注油箱、铂电阻及热电偶、压力表、调节阀及放空排放阀等构成。实验装置中主要设备及仪表见表 1。实验流程主要包括导热油加注、系统预热及查漏、水箱冷却水加注、加热循环排不凝气、设定实验工况、进行实验、实验结束后冷却降温等。实验时,加热至设定温度的导热油通过离心泵、流量计及阀门进入C型换热管,与水箱内的冷却水进行换热,之后返回导热油罐。在不断循环加热过程中,水箱内水温逐步升高,并逐步由自然对流过渡至过冷沸腾以及饱和沸腾。当整个水箱内的水温达到饱和沸腾(在本实验中,考虑到上海地区的海拔高度接近于海平面,因而对应大气压下水的饱和温度按照100 ℃计)并持续15 min后,结束实验并降温。
|
图 1 单管传热实验装置工艺流程图 Fig.1 Flow diagram of heat transfer experimental setup with single tubes 1. water tank 2. C-tube 3. thermocouples 4. pump 5. flow meter 6. oil tank 7. oil filling port 8. electric heater |
|
|
表 1 实验装置主要设备及仪表清单 Table 1 Main equipment used in this study |
实验过程中,测温热电偶读数通过数据采集仪进行采集,导热油流量计用来实时测量流量,控制柜用来控制导热油泵以及电加热器的开关,同时通过温度控制器来自动控制电加热器。所有热电偶在使用前均进行了标定,其他仪器根据使用说明书的要求进行了调校。高速摄像机用来对换热管表面的汽泡产生及运动过程进行跟踪拍摄,通过专用软件进行观察及数据存储。此外,水箱外壁及底部分别安装了厚度为25 mm的橡塑保温板(常温导热系数0.035 W·m−1·℃−1),水箱顶部安装了具有冷却功能的盖子,用以冷却蒸汽并回流以控制水位基本稳定。考虑到保温材料导热系数很低,并且实验过程蒸发量很小,因而热量散失以及液位变化对实验结果的影响可忽略不计。
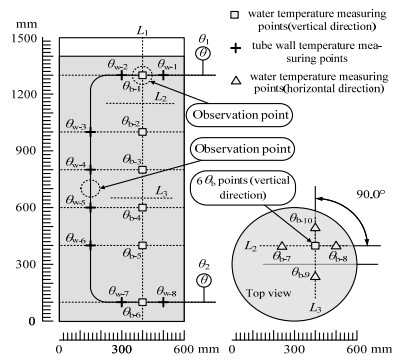
图 2为热电偶分布图,其中包括油温测量点、管外壁温测量点以及水温测量点(水平及竖直方向)。在水箱外部进出口位置分别有一个油温测量点θ1和θ2,管外壁温测量点(θw-1到θw-8)共计8个,其中竖直段4个,分布间距为200 mm,上下水平段各2个,分布间距为200 mm,壁温测量点在每个位置的圆周上共安装3个热电偶,间隔120°均布,采用焊接方法安装,在计算时取算术平均值。水温测量点(竖直方向)一共有6个(θb-1到θb-6),其中θb-1和上水平段壁温测量点θw-1及θw-2处于同一高度,θb-6和下水平段壁温测量点θw-7及θw-8处于同一高度,其他测量点分别与竖直段管外壁温测量点高度一一对应,且6个测量点均位于图 2中的L1直线上。水温测量点(水平方向)一共4个热电偶,其中2个(θb-7和θb-8)分布在图 2中L2高度,另外2个(θb-9和θb-10)分布在L3高度,在每个高度上的分布情况见俯视图。另外,观测点分别设置在上水平段θw-1与θw-2壁温测量点中间位置以及竖直段θw-4与θw-5壁温测量点中间位置。
|
图 2 热电偶分布图 Fig.2 Thermocouple distribution diagram |
在本实验中,导热油物性参数见表 2,该导热油闪点不低于220 ℃。表中,θ为温度,℃。在入口体积流量2.0 m3·h−1、入口温度167.5 ℃及初始水温35.0 ℃的工况下,进行多组重复性实验,最大偏差在10% 以内。
|
|
表 2 导热油物性参数 Table 2 Physical properties of thermal oil |
在实验中通过数据采集系统可以直接得到的参数有:导热油进出换热管的温度、流量、换热管外壁温以及水箱内冷却水温度等。在本实验中,考虑到导热油进出口温度差不超过11 ℃,物性变化很小,因此通过热量平衡并结合牛顿冷却定律,传热过程计算公式为
| $ \varPhi = {q_m}{c_p}\Delta \theta = \varphi A = hA\left( {{\theta _{\text{w}}} - {\theta _{\text{b}}}} \right) $ | (1) |
式中:Φ为热流量,W;qm为质量流量,kg·s−1;cp为比定压热容,J·kg−1·℃−1;Δθ为温差,℃;φ为热流密度,W·m−2;h为传热系数,W·m−2·℃−1;A为换热管有效换热面积,m2;θw为壁温,℃;θb为主流流体温度,℃。
此外,对整个实验系统进行误差分析[11],其中最大温度偏差为±0.51 ℃,流量偏差为±0.02 m3·h−1,换热量、热流密度及传热系数中最大偏差约为3.5%。
3 实验结果与讨论根据Liu等[12]研究结果,首先判断得到实验工况下对应的过冷沸腾起始点,对自然对流及过冷沸腾阶段进行区分,进而可以针对过冷沸腾阶段的传热特性开展研究。考虑到本研究为C型管结构,且上水平段与下水平段具有一定的相似性,因而为了便于分析,分别选取上水平段及竖直段观测点位置的换热开展下述研究。
3.1 管外过冷沸腾传热动态特性水平观测点位置4个时刻的参数值见表 3。表中,t为时间,s;
|
|
表 3 水平观测点位置4个时刻的参数值 Table 3 Parameter values at the horizontal observation point under four different observation times |
竖直观测点位置4个时刻的参数值见表 4。几个参数的变化规律与水平段观测点位置具有一定的相似性,随着时间的延长,壁温、冷却水温度以及管外传热系数均持续升高,观测过程发现,汽泡形成数量持续增加,直径不断增大,当达到一定尺寸后开始与壁面分离并扩散至主流区域。另外从表 4也可以看到,壁面过热度随着时间的延长持续增大,冷却水的过冷度则逐渐减小。整个过冷沸腾阶段,水温由84.7 ℃逐步上升至饱和温度;传热系数相对较低,在2 876.9~8 742.2 W·m−2·℃−1持续增大;过冷度由15.3 ℃减小至接近0 ℃,壁温及过热度的变化同样在2.0 ℃内。
|
|
表 4 竖直观测点位置4个时刻的参数值 Table 4 Parameter values at the vertical observation point under four different observation times |
此外,根据水箱内2个不同高度(L2及L3)分别对应的2个测温热电偶(θb-7和θb-8,θb-9和θb-10)读数发现,同一时刻对应的最大偏差在2 ℃以内,说明在水箱内同一高度,冷却水混合较为均匀。
3.2 管外过冷沸腾传热计算 3.2.1在
最早提出叠加模型的是Rohsenow[9]以及Chen[13],主要用于管内核态流动沸腾的传热计算,后续逐步被扩展至管内及管外流动过冷沸腾工况。以上述两人提出的经验公式为基础,后续有相关研究提出改进或修正的叠加模型,适用范围各有不同。在流动过冷沸腾叠加模型中,叠加的2个热流密度或传热系数分别为单相对流传热以及饱和沸腾传热对应值,两个系数F及S分别为雷诺数影响因子及削弱系数,在不同的研究中分别对应不同的设定值或函数式,分别代表流动对传热的加强或削弱作用。文献中报道的多为与雷诺数Re关联的F及S,并不适用于本研究中的池内沸腾。故而选择Rohsenow[9]叠加公式进行对比
| $ \varphi = {h_{{\text{sp}}}}\left( {{\theta _{\text{w}}} - {\theta _{\text{b}}}} \right) + {h_{{\text{nb}}}}\left( {{\theta _{\text{w}}} - {\theta _{{\text{sat}}}}} \right) $ | (2) |
式中:hsp及hnb分别为自然对流传热系数及饱和沸腾传热系数,W·m−2·℃−1;θsat为流体饱和温度,℃。
想要验证公式(2)适用与否,第一步需要对应选择合适的管外自然对流传热经验公式以及饱和沸腾经验公式,用来计算hsp以及hnb。
(1) 管外自然对流传热
针对水平及竖直段分别选取对应的经验公式,并利用自然对流阶段的实验数据,将预测结果与实验计算结果对比,选择适合的传热计算公式。
(a) 水平段
对水平换热管或壁面自然对流传热的研究已经比较成熟,选择Churchill[14]、Churchill & Chu[15]、Mcadams[16]、Eckert & Jackson[17]等4个关联度高的公式,将预测的努塞尔数Nu与实验计算努塞尔数Nu对比分析。如图 3所示为水平段自然对流经验公式预测Nu与实验计算Nu对比,从图中可看出,各个经验公式预测结果在变化趋势上比较一致。其中,预测准确性最好的是Eckert & Jackson[17]经验公式。统计结果显示Eckert & Jackson[17]经验公式对Nu的预测偏差均分布在±15% 以内。

|
图 3 水平段自然对流经验公式预测Nu与实验计算Nu对比 Fig.3 Comparison of predicted and experimental Nu of natural convection at the horizontal section |
(b) 竖直段
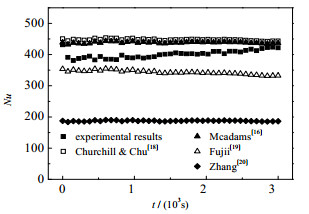
对竖直换热管或壁面进行的自然对流传热,选择了关联度高的Churchill & Chu[18]、Mcadams[16]、Fujii[19]及Zhang[20]等4个经验公式,将预测结果与实验计算结果对比分析。如图 4所示为竖直段自然对流经验公式预测的Nu与实验计算的Nu对比,从图中可看出,不同经验公式预测结果也具有十分明显的差异。其中Zhang[20]经验公式预测结果最低且与实验计算结果偏离最大,Fujii[19]经验公式预测结果同样偏低;Churchill & Chu[18]、Mcadams[16]两个经验公式预测结果略高于实验计算结果,通过偏差分析发现预测准确性最好的是Mcadams[16]经验公式。统计结果显示Mcadams[16]经验公式对Nu的预测偏差集中在0~+15%。
|
图 4 竖直段自然对流经验公式预测Nu与实验计算Nu对比 Fig.4 Comparison of predicted and experimental Nu of natural convection at the vertical section |
(2) 管外饱和沸腾传热
对水平及竖直段管外饱和沸腾传热计算分别选择了适合的经验公式。利用冷却水温度达到饱和温度后的实验数据,分别计算并对比。对于水平段,选取了Jakob & Hawkins[21]、Mostinski[22]、Stephan & Abdelsalam[23]、Cornwell[24]、Cooper[25]以及Corletti[26]共计6个经验公式,并将预测的传热系数与实验计算得到的传热系数进行比较;对于竖直段,选择了Rohsenow[27]、Mostinski[22]、Cornwell[24]、Gupta[28]、Zhang[29]以及Tian[30]共计6个经验公式,并将预测的传热系数与实验计算得到的传热系数进行比较。
(a) 水平段
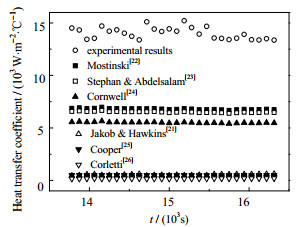
对于水平段,饱和沸腾经验公式预测h与实验计算h对比见图 5。从图中可看出,6个经验公式的预测h均明显低于实验计算h。其中Jakob & Hawkins[21]、Cooper[25]以及Corletti[26]经验公式预测结果较为接近,但与实验计算值差异最大;而Mostinski[22]、Stephan & Abdelsalam[23]以及Cornwell[24]经验公式预测结果较为接近,但与实验计算结果的差异依然很大。因此6个经验公式均不能准确预测实验工况下的传热系数h。分析原因,一方面所选用的经验公式在形式上具有较大的不同,各自提出的基础存在差异,有的是基于理论并结合实验数据进行拟合,有的则更多地依靠实验积累的数据,分析规律得出;另一方面,不同经验公式对应的实验工况也有差异,在推广至其他工况时则不一定适用。利用Origin软件通过非线性拟合方法,得到h与
|
图 5 水平段饱和沸腾经验公式预测h与实验计算h对比 Fig.5 Comparison of predicted and experimental h of saturated boiling at the horizontal section |
| $ {h}_{\text{nb}}=75\text{ }352.2\Delta {\theta }_{\text{sat}}{}^{-1.113\text{ }72}\left({4.2}_{}℃\le \Delta {\theta }_{\text{sat}}\le {4.9}_{}℃\right) $ | (3) |
如图 6所示为水平段饱和沸腾拟合经验公式对h的预测偏差,从图中可看出,预测偏差均处于±5% 以内。
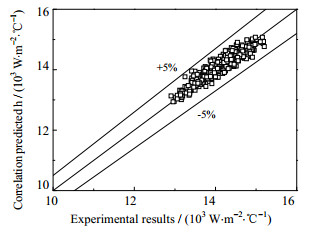
|
图 6 水平段饱和沸腾拟合经验公式对h的预测偏差 Fig.6 Predicted errors of h with fitted saturated boiling correlation at the horizontal section |
(b) 竖直段
对于竖直段,饱和沸腾经验公式预测h与实验计算h对比见图 7。从图中可看出,Rohsenow[27]、Mostinski[22]、Cornwell[24]、Gupta[28]以及Tian[30]经验公式预测h均低于实验计算h,只有Zhang[29]经验公式预测结果略高于实验计算值。在所有曲线中,传热系数随时间变化趋势均比较稳定,说明该阶段已经达到了稳定的饱和沸腾。对比分析发现,Rohsenow[27]经验公式预测结果与实验计算结果的吻合情况最佳,平均偏差为14.5%。
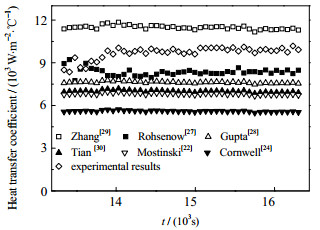
|
图 7 竖直段饱和沸腾经验公式预测h与实验计算h对比 Fig.7 Comparison of predicted and experimental h of saturated boiling at the vertical section |
(3) 与Rohsenow[9]叠加模型的计算对比
Rohsenow[9]叠加模型对φ的预测偏差见图 8。可以看出,该模型预测结果与实验计算结果的偏差分布比较零散,大约37% 的预测结果分布于±15% 偏差线以外。这说明该模型对管外过冷沸腾热流密度的预测准确性不高。
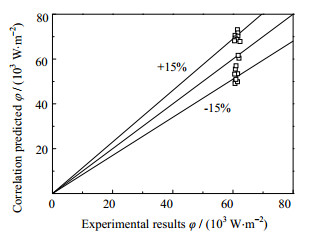
|
图 8 Rohsenow[9]叠加模型对φ的预测偏差 Fig.8 Predicted errors of φ with Rohsenow superposition correlation |
针对池内过冷沸腾,Jeon等[10]认为汽泡产生机理与饱和沸腾传热机理在根本上是相同的,因而提出将饱和沸腾经验公式与削弱系数相结合的办法来预测过冷沸腾传热。故而提出削弱系数模型
| $ {h_{{\text{sub}}}} = S \cdot {h_{{\text{nb}}}} $ | (4) |
式中:传热系数hnb分别采用水平段饱和沸腾经验公式(3)及竖直段对应的Rohsenow[27]经验公式计算;指数z通过实验数据拟合得到。削弱系数S(≤1)定义为
| $ S = {\left( {1 + {{\Delta {\theta _{{\text{sub}}}}} \mathord{\left/ {\vphantom {{\Delta {\theta _{{\text{sub}}}}} {\Delta {\theta _{{\text{sat}}}}}}} \right. } {\Delta {\theta _{{\text{sat}}}}}}} \right)^{ - z}} $ | (5) |
利用实验数据,并且为了提高适用性,结合上述削弱系数模型分别对水平及竖直段利用Origin软件进行非线性拟合。
(1) 水平段z=1.139
| $ {h}_{\text{sub}}={\left(1+\Delta {\theta }_{\text{sub}}/\Delta {\theta }_{\text{sat}}\right)}^{-1.139}\cdot {h}_{\text{nb}}{{}_{}}_{}\left(3.0℃\le \Delta {\theta }_{\text{sat}}\le 4.5℃{, }_{}{}_{}0℃<\Delta {\theta }_{\text{sub}}\le 4.9℃\right) $ | (6) |
如图 9所示为水平段过冷沸腾拟合经验公式对h的预测偏差,从图中可看出,最大偏差3.6%,平均偏差1.9%。
|
图 9 水平段过冷沸腾拟合经验公式对h的预测偏差 Fig.9 Predicted errors of h with fitted subcooled boiling correlation at the horizontal section |
(2) 竖直段z=0.306
| $ {h}_{\text{sub}}={\left(1+\Delta {\theta }_{\text{sub}}/\Delta {\theta }_{\text{sat}}\right)}^{-0.306}\cdot {h}_{\text{nb}}\left(5.9℃\le \Delta {\theta }_{\text{sat}}\le 7.1℃, 0℃<\Delta {\theta }_{\text{sub}}\le 15.3℃\right) $ | (7) |
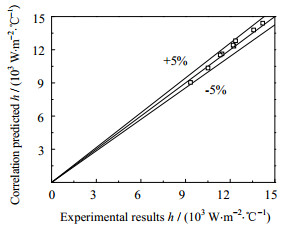
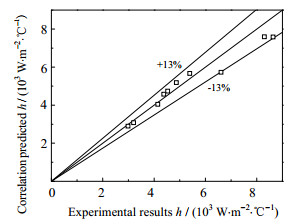
如图 10所示为竖直段过冷沸腾拟合经验公式对h的预测偏差,从图中可看出,最大偏差13.3%,平均偏差6.4%。
|
图 10 竖直段过冷沸腾拟合经验公式对h的预测偏差 Fig.10 Predicted errors of h with fitted subcooled boiling correlation at the vertical section |
实验研究了单根C型管外过冷沸腾传热动态特性。分析过冷沸腾阶段相关重要参数的变化规律,利用多种模型及经验公式对管外过冷沸腾阶段的传热进行预测及分析。主要结论有:
(1) C型管水平及竖直观测点位置对应的传热特性差异明显。实验结果表明:相比竖直观测点,水平观测点对应的传热更为剧烈,传热系数更高,对应水温上升更为迅速,且过冷沸腾所需过热度更低。
(2) 对实验工况下水平及竖直观测点位置管外过冷沸腾采用
(3) 在采用叠加模型进行预测分析的过程中,对自然对流及饱和沸腾传热预测经验公式的适用性进行了判定。分析得出了水平段管外自然对流传热适用性最好的是Eckert & Jackson[17]经验公式,竖直段适用性最好的为Mcadams[16]经验公式。竖直段管外饱和沸腾传热适用性最好的为Rohsenow[27]经验公式,对于水平段管外饱和沸腾传热,拟合了预测更加准确的经验公式
| [1] |
纪献兵, 王野, 代超, 等. 乳突状多尺度结构表面的池沸腾传热特性[J]. 高校化学工程学报, 2018, 32(2): 312-318. JI X B, WANG Y, DAI C, et al. Pool boiling heat transfer characteristics on mastoid surface with multiscale structures[J]. Journal of Chemical Engineering of Chinese Universities, 2018, 32(2): 312-318. DOI:10.3969/j.issn.1003-9015.2018.02.009 |
| [2] |
SCHULZ T L. Westinghouse AP1000 advanced passive plant[J]. Nuclear Engineering and Design, 2006, 236(14/15/16): 1547-1557. |
| [3] |
LIU Y B, WANG X S, MENG X Y, et al. A review on tube external heat transfer for passive residual heat removal heat exchanger in nuclear power plant[J]. Applied Thermal Engineering, 2019, 149: 1476-1491. DOI:10.1016/j.applthermaleng.2018.11.114 |
| [4] |
HATA K, MASUZAKI S. Critical heat fluxes of subcooled water flow boiling in a short vertical tube at high liquid Reynolds number[J]. Nuclear Engineering and Design, 2010, 240(10): 3145-3157. DOI:10.1016/j.nucengdes.2010.05.035 |
| [5] |
MCADAMS W H, KENNEL W E, MINDEN C S, et al. Heat transfer at high rates to water with surface boiling[J]. Industrial and Engineering Chemistry, 1949, 41(9): 1945-1953. DOI:10.1021/ie50477a027 |
| [6] |
JENS W H, LOTTES P A. An analysis of heat transfer, burnout, pressure drop and density data for high pressure water [R]. Chicago: Argonne National Laboratory, 1951.
|
| [7] |
THOM J R S, WALKER W M, FALLON T A, et al. Boiling in subcooled water during flow up heated tubes or annuli: Proceedings of the Institution of Mechanical Engineers [C]. London: SAGE Publications, 1965: 226-246.
|
| [8] |
ALADIEV I T, DODONOV L D, UDALOV U S. Heat transfer at subcooled water boiling in tubes[J]. Teploenergetika, 1957, 4(9): 9-23. |
| [9] |
ROHSENOW W M. Heat transfer with evaporation: A Symposium held at the University of Michigan [C]. East Lansing: University of Michigan Press, 1952: 101-150.
|
| [10] |
JEON S S, HONG S J, CHO H K, et al. Prediction of nucleate boiling heat transfer on horizontal U-shaped heat exchanger submerged in a pool of water using MARS code[J]. Nuclear Engineering and Design, 2015, 295: 317-337. DOI:10.1016/j.nucengdes.2015.09.029 |
| [11] |
张煜, 李端勇. 大学物理实验[M]. 北京: 科学出版社, 2014. ZHANG Y, LI D Y. Experiment of college physics[M]. Beijing: Science Press, 2014. |
| [12] |
LIU Y B, MENG X Y, WANG X S, et al. Judgement and calculation method research of onset of nucleate boiling under tube outside pool boiling condition: IOP Conference Series: Earth and Environmental Science [C]. Bristol: IOP Publishing, 2021: 1-8.
|
| [13] |
CHEN J C. Correlation for boiling heat transfer to saturated fluids in convective flow[J]. Industrial Engineering Chemistry Process Design and Development, 1966, 5(3): 322-329. DOI:10.1021/i260019a023 |
| [14] |
CHURCHILL S W. Laminar free convection from a horizontal cylinder with a uniform heat flux density[J]. Letters in Heat and Mass Transfer, 1974, 1(2): 109-112. DOI:10.1016/0094-4548(74)90146-5 |
| [15] |
CHURCHILL S W, CHU H S. Correlating equations for laminar and turbulent free convection from a horizontal cylinder[J]. International Journal of Heat and Mass Transfer, 1975, 18(9): 1049-1053. DOI:10.1016/0017-9310(75)90222-7 |
| [16] |
MCADAMS W H. Heat transmission[M]. New York: McGraw-Hill, 1954.
|
| [17] |
ECKERT E R G, DRAKE R M. Analysis of heat and mass transfer[M]. New York: McGraw-Hill, 1972.
|
| [18] |
CHURCHILL S W, CHU H S. Correlating equations for laminar and turbulent free convection from a vertical plate[J]. International Journal of Heat and Mass Transfer, 1975, 18(11): 1323-1329. DOI:10.1016/0017-9310(75)90243-4 |
| [19] |
FUJII T, TAKEUCHI M, FUJII M, et al. Experiments on natural-convection heat transfer from the outer surface of a vertical cylinder to liquids[J]. International Journal of Heat and Mass Transfer, 1970, 13(5): 753-770. DOI:10.1016/0017-9310(70)90125-0 |
| [20] |
张钰浩, 陆道纲, 王忠毅, 等. AP1000非能动余热排出热交换器缩比C型管束二次侧传热模型实验研究[J]. 原子能科学技术, 2016, 50(10): 1763-1770. ZHANG Y H, LU D G, WANG Z Y, et al. Experimental investigation on heat transfer model for secondary side of scale C-shape bundle used in PRHR HX of AP1000[J]. Atomic Energy Science and Technology, 2016, 50(10): 1763-1770. DOI:10.7538/yzk.2016.50.10.1763 |
| [21] |
JAKOB M, HAWKINS G A. Elements of heat transfer[M]. New York: John Wiley and Sons, 1957.
|
| [22] |
MOSTINSKI I L. Application of the rule of corresponding states for calculation of heat transfer and critical heat flux[J]. Teploenergetika, 1963, 4(4): 66-71. |
| [23] |
STEPHAN K, ABDELSALAM M. Heat transfer correlations for natural convection boiling[J]. International Journal of Heat Mass Transfer, 1980, 23(1): 13-87. |
| [24] |
CORNWELL K, SCHULLER R B, EINARSSON J. The influence of diameter on nucleate boiling outside tubes: Proceeding of the 7th International Heat Transfer Conference [C]. Washington: Hemisphere Publishing, 1982: 47-53.
|
| [25] |
COPPER M G. Heat flow rates in saturated nucleate pool boiling-a wide-ranging examination using reduced properties[J]. Advances in Heat Transfer, 1984, 16: 157-239. |
| [26] |
CORLETTI M M, HOCHREITER L E, SQUARER D. AP600 passive residual heat removal heat exchanger test[J]. Transactions of the American Nuclear Society, 1990, 62: 669-671. |
| [27] |
ROHSENOW W M. A method of correlating heat transfer data for surface boiling of liquids[J]. Transactions of ASME, 1952, 74: 969-976. |
| [28] |
GUPTA A, KUMAR R, KUMAR V. Nucleate pool boiling heat transfer over a bundle of vertical tubes[J]. International Communications in Heat and Mass Transfer, 2010, 37(2): 173-181. |
| [29] |
ZHANG Y H, LU D G, WANG Z Y, et al. Experimental investigation on pool-boiling of C-shape heat exchanger bundle used in PRHR HX[J]. Applied Thermal Engineering, 2017, 114: 186-195. DOI:10.1016/j.applthermaleng.2016.11.185 |
| [30] |
TIAN Y S, CHEN Z Q, WANG N H, et al. Experimental investigations on pool boiling on a vertical tube in the confined and unconfined spaces[J]. Applied Thermal Engineering, 2018, 133: 107-116. DOI:10.1016/j.applthermaleng.2018.01.043 |




