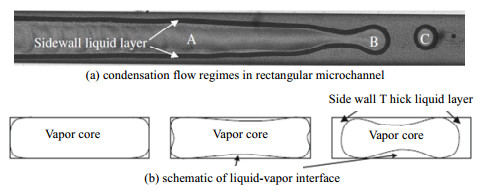
随着热控制系统的高能量密度化和小型化,微通道内流动凝结成为微型反应器、微型冷凝器和微型热管等设备中的关键热物理过程。对于微通道内气液两相流,表面张力相对重力起主导作用[1],使微通道内流动凝结换热特性显著区别于常规通道。由于使用深反应离子刻蚀方法在硅片上加工方便[2-3],矩形微通道已在微型热设备中大量使用。Zhang等[4-5]研究了在水力直径为57.8 μm、宽深比为26.7的宽矩形硅基微通道内水蒸气流动凝结,发现气泡脱离环状流存在单液丝断裂、双液丝同步断裂和双液丝非同步断裂三种模式。Chen和Wu等[6-7]研究了水蒸气在水力直径为90.6 μm、宽深比为9.668的宽矩形硅基微通道内流动凝结,观测到三角形和梯形通道内没有出现的珠状-环状复合流。Fang等[8]研究了水蒸气在水力直径为100~300 μm,不同宽高比的矩形硅基微通道内流动凝结,发现在相同流量下增大矩形微通道宽高比可提高平均壁面热流密度。Ma等[9]对水蒸气在水力直径为134.52~165.87 μm、宽高比为3.8~7.4的梯形硅基微通道内流动凝结的研究发现截面形状对流型分布有重要影响,绘制了不同截面形状通道的流型图。Quan等[10]研究了水蒸气在水力直径为90~136 μm,宽高比为2.44~9.8的梯形硅基微通道内流动凝结,发现环波状流只出现在宽高比较小的梯形微通道内。然而宽高比对微通道内流动凝结换热特性的影响机理尚未清楚。
由于水力直径小,难以直接测量微通道内物理参数分布。通过数值模拟可深入揭示流动凝结的物理机制。Wang等[11-14]对R134a,R22和R410a在水力直径为0.33~1.2 mm的圆形、矩形、三角形通道内流动凝结进行了稳态模拟,发现非圆通道比圆管具有更好的换热性能。Wu等[15]在等热流密度下数值模拟了水蒸气在水力直径为100 μm的矩形微通道内环状流区域的流动凝结,指出环状流下游的换热系数不变。Hao等[16]对水蒸气在水力直径为100~333 μm的梯形、矩形和三角形微通道内流动凝结的稳态数值模拟发现在相同工况下,矩形微通道的环状流区域短于梯形和三角形。Mghari等[17]对水蒸气在水力直径为80~250 μm的矩形微通道内流动凝结的稳态数值模拟发现增大固液接触角能强化换热。
由于微通道内流动凝结是一个非稳态过程,流场参数随时间变化,需建立相应的瞬态数值模型。Ganapathy等[18]对R134a在内径为100 μm的微圆管内流动凝结进行了二维瞬态数值模拟,存在不足之处为进口不出现凝结,并且环状流区域不是薄液膜区域。
本文提出一种模拟矩形微通道内流动凝结的瞬态数值模型。通过捕捉气液界面运动发展过程,揭示宽高比对凝结换热特性、界面波动与喷射流的影响规律,以指导微通道冷凝器的设计与优化。
2 数值模型 2.1 VOF模型VOF模型能够模拟不相混合的多相流动,可追踪界面的运动发展过程。对于纯工质的气液两相流动,计算单元内气、液相所占的体积分数分别为
| ${\alpha _{\rm{v}}}{\rm{ + }}{\alpha _{\rm{l}}} = 1$ | (1) |
计算单元内气液相混合物的密度
| $ \rho = {\alpha _{\rm{l}}}{\rho _{\rm{l}}} + {\alpha _{\rm{v}}}{\rho _{\rm{v}}} $ | (2) |
| $ \lambda = {\alpha _{\rm{l}}}{\lambda _{\rm{l}}} + {\alpha _{\rm{v}}}{\lambda _{\rm{v}}} $ | (3) |
| $ \mu = {\alpha _{\rm{l}}}{\mu _{\rm{l}}} + {\alpha _{\rm{v}}}{\mu _{\rm{v}}} $ | (4) |
| $ E = \frac{{{\alpha _{\rm{l}}}{\rho _{\rm{l}}}{E_{\rm{l}}} + {\alpha _{\rm{v}}}{\rho _{\rm{v}}}{E_{\rm{v}}}}}{{{\alpha _{\rm{l}}}{\rho _{\rm{l}}} + {\alpha _{\rm{v}}}{\rho _{\rm{v}}}}} $ | (5) |
即密度、热导率、动力黏度是强度量,采用体积平均法得到;而热力学能是广延量,需采用质量平均法得到比热力学能。
气液界面邻域的控制方程如下:
(1) VOF方程
| $ \frac{{\partial ({\alpha _{\rm{v}}}{\rho _{\rm{v}}})}}{{\partial t}} + \nabla \cdot ({\alpha _{\rm{v}}}{\rho _{\rm{v}}}{\boldsymbol{u}}) = {S_{\rm{v}}} $ | (6) |
| $ \frac{{\partial ({\alpha _{\rm{l}}}{\rho _{\rm{l}}})}}{{\partial t}} + \nabla \cdot ({\alpha _{\rm{l}}}{\rho _{\rm{l}}}{\boldsymbol{u}}) = {S_{\rm{l}}} $ | (7) |
式中
(2) 连续方程
| $ \frac{{\partial \rho }}{{\partial t}} + \nabla \cdot (\rho {\boldsymbol{u}}) = 0 $ | (8) |
(3) 动量方程
| $ \frac{{\partial (\rho \mathit{\boldsymbol{u}})}}{{\partial t}} + \nabla \cdot (\rho \mathit{\boldsymbol{uu}}) =- \nabla p + \nabla \cdot [\mu (\nabla \mathit{\boldsymbol{u}} + \nabla {\mathit{\boldsymbol{u}}^{\rm{T}}})] + \rho \mathit{\boldsymbol{g}} + {\mathit{\boldsymbol{F}}_{{\rm{vol}}}} $ | (9) |
式中采用Brackbill等[19]提出的CSF模型将表面张力作用转换为体积力
| ${\mathit{\boldsymbol{F}}_{{\rm{vol}}}} = \sigma \frac{{{\alpha _{\rm{l}}}{\rho _{\rm{l}}}{\kappa _{\rm{l}}}\nabla {\alpha _{\rm{l}}} + {\alpha _{\rm{v}}}{\rho _{\rm{v}}}{\kappa _{\rm{v}}}\nabla {\alpha _{\rm{v}}}}}{{0.5({\rho _{\rm{l}}} + {\rho _{\rm{v}}})}} = \sigma \frac{{2\rho {\kappa _{\rm{l}}}\nabla {\alpha _{\rm{l}}}}}{{{\rho _{\rm{l}}} + {\rho _{\rm{v}}}}} $ | (10) |
式中,
| $ {\kappa _{\rm{l}}} =-{\kappa _{\rm{v}}} = \nabla \cdot \mathit{\boldsymbol{n}}$ | (11) |
式中,n为单位法向量,表达式为
| $\mathit{\boldsymbol{n}} = \frac{{\nabla {\alpha _{\rm{l}}}}}{{\left| {\nabla {\alpha _{\rm{l}}}} \right|}} $ | (12) |
(4) 能量方程
| $ \frac{{\partial (\rho E)}}{{\partial t}} + \nabla \cdot [\mathit{\boldsymbol{u}}(\rho E + p)] = \nabla \cdot (\lambda \nabla T) + Q $ | (13) |
式中Q是由于气液相变导致的能量源项,J·m-3·s-1。
| $ Q = {S_{\rm{l}}}{h_{{\rm{fg}}}} =-{S_{\rm{v}}}{h_{{\rm{fg}}}} $ | (14) |
对于纯工质的凝结换热,气液界面温度约等于饱和温度Ts。根据气体分子运动理论和纯工质的克拉贝隆方程,凝结速率由质量源项[20]表示:
| $ {S_{\rm{l}}} = \left\{ {\begin{array}{*{20}{l}} {r{\alpha _{\rm{v}}}{\rho _{\rm{v}}}\frac{{{T_{\rm{s}}}-T}}{{{T_{\rm{s}}}}}\;\;\;\;\;\left( {T < {T_{\rm{s}}}} \right)}\\ {r{\alpha _{\rm{l}}}{\rho _{\rm{l}}}\frac{{{T_{\rm{s}}}-T}}{{{T_{\rm{s}}}}}\;\;\;\;\;\;\;\left( {T \ge {T_{\rm{s}}}} \right)} \end{array}} \right. $ | (15) |
| $ {S_{\rm{v}}} =-{S_{\rm{l}}} $ | (16) |
式中r为正的经验系数,s-1。多次计算结果表明:增加r能有效减小气液界面温度与饱和温度的差值,这使得计算结果满足气液界面温度约等于饱和温度的物理关系。但过大的r值会导致计算不稳定,甚至发散。本文根据网格尺度和时间步长,通过尝试性计算后将r设置为3.33×109 s-1,气液界面温度与饱和温度的差值控制在0.1 K以内。
2.3 模拟工况与求解方法采用Fluent14.5进行求解计算。计算域及边界条件如图 1所示,矩形微通道内计算域为0≤x≤a μm,0≤y≤b μm,-0.3≤z≤1 mm,考虑重力影响,重力作用方向为y轴负方向。考虑到模拟进口干度为1的气相完全凝结过程需要占用大量计算资源,本文矩形微通道进口处设置为饱和温度为60℃的R32气液两相流,干度x为0.4。在微通道内与重力相比,表面张力主导气液两相流动形态,因此假定液膜在速度进口处均匀分布,厚度

|
图 1 矩形微通道计算域与边界条件 Fig.1 Computational domain and boundary conditions of the rectangular microchannel |
|
|
表 1 三种矩形微通道监测面气液相分布 Table 1 Gas-liquid distribution on monitoring surfaces in the three rectangular microchannels |
基于分相模型,进口气相和液相速度取平均速度,大小分别为
| $ {u_{\rm{v}}} = \frac{{xGab}}{{{\rho _{\rm{v}}}(a-2\delta )(b-2\delta )}} $ | (17) |
| $ {u_{\rm{l}}} = \frac{{(1- x)Gab}}{{{\rho _{\rm{l}}}[ab-(a-2\delta )(b-2\delta )]}} $ | (18) |
式中G为质量流率,kg·m-2·s-1。进口气相和液相Re数分别为
| $ R{e_{\rm{v}}} = \frac{{2abGx}}{{(a + b){\mu _{\rm{v}}}}} $ | (19) |
| $ R{e_{\rm{l}}} = \frac{{2abG(1-x)}}{{(a + b){\mu _{\rm{l}}}}} $ | (20) |
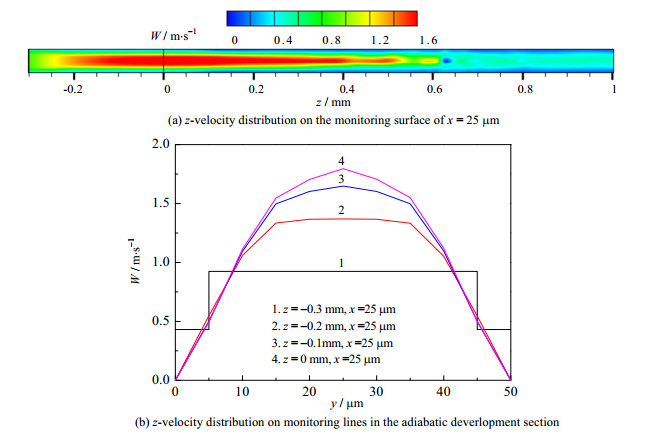
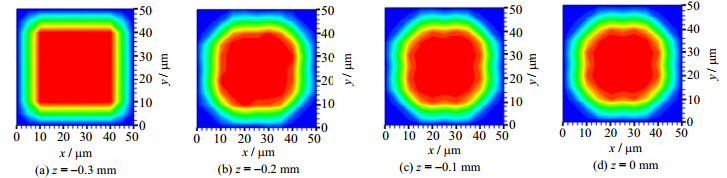
以a = b= 50 μm为例,当G≤500 kg·m-2·s-1,Rev≤626且Re1≤210,气相和液相均为层流。本文模拟取G = 200 kg·m-2·s-1。考虑到实际等壁温凝结段初始断面(z = 0 mm)上气相和液相速度并非均匀分布,且由于表面张力梯度作用,液膜分布不均匀,数值模拟设置绝热发展段(-0.3≤z≤0 mm)长度为0.3 mm,使得气液两相流在进入等壁温凝结段(0≤z≤1 mm)之前达到充分发展状态。由图 2(b)、3(b)与4可得速度和液膜分布与实际情况相符较好。
|
图 3 a = b = 50 μm矩形通道监测面与监测线z方向速度分布 Fig.3 z-velocity distribution on monitoring surface and along lines in the rectangular microchannel with a = b = 50 μm |
|
图 4 a = b = 50 μm矩形通道监测面气液分布 Fig.4 Gas-liquid distribution on monitoring surfaces in the rectangular microchannel with a = b = 50 μm |
选取尺寸为2和5 μm的正方形网格进行网格无关性验证,平均壁面热流密度偏差小于2%,因此选用5 μm的正方形网格系统。使用Co数执行可变时间步长求解方法:
| $ Co = \frac{{\delta t}}{{\delta x/u}} $ | (21) |
式中,
表 1显示了三种矩形微通道内不同监测面气液相分布模拟结果,矩形微通道内计算域为0≤x≤a μm,0≤y≤b μm,-0.3≤z≤1 mm。等壁温凝结段(0≤z≤1 mm)依次出现的流型为环状流、喷射流、泡状流,与图 2所示的实验结果定性上吻合较好。
以a = b = 50 μm矩形通道为例研究绝热发展段气液相速度与液膜的发展过程。由于进口段效应,液膜减速(见图 3),通道截面液相面积增大(见图 4)。由图 3可知绝热发展段(-0.3≤z≤0 mm)监测面Z方向速度分布可知气液两相速度已趋于充分发展状态。图 4显示绝热发展段内液膜发展过程:表面张力导致液膜内部产生压力梯度,驱使液相流向通道壁面拐角处。由图 4(c)和4(d)可知液膜已趋于充分发展状态。因此,等壁温凝结段起始截面(z = 0 mm)的速度和液膜分布接近实际情况。
综上所述,该数值模型能较为准确地模拟实际微通道内流动凝结过程。
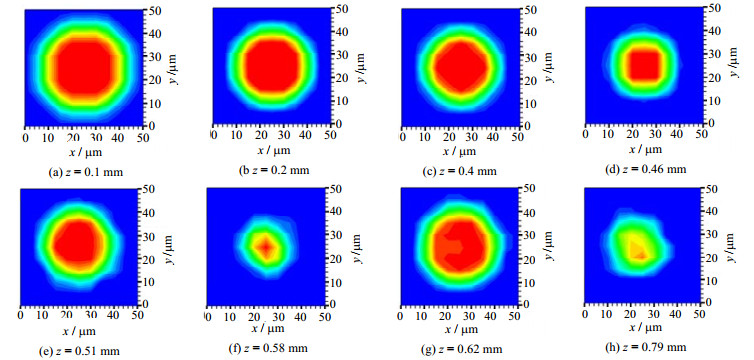
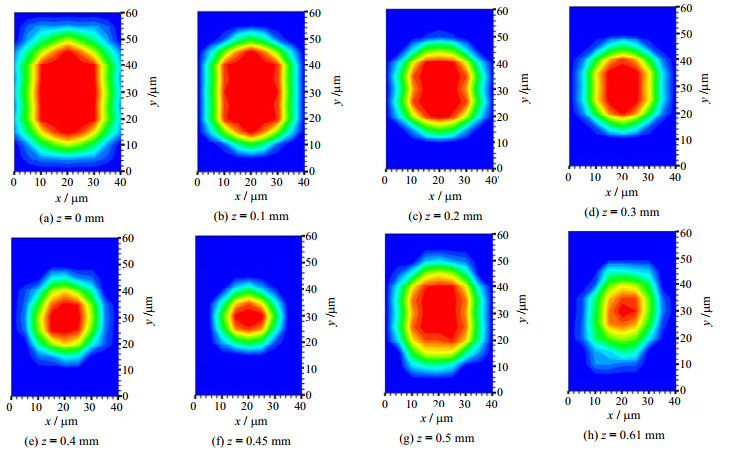
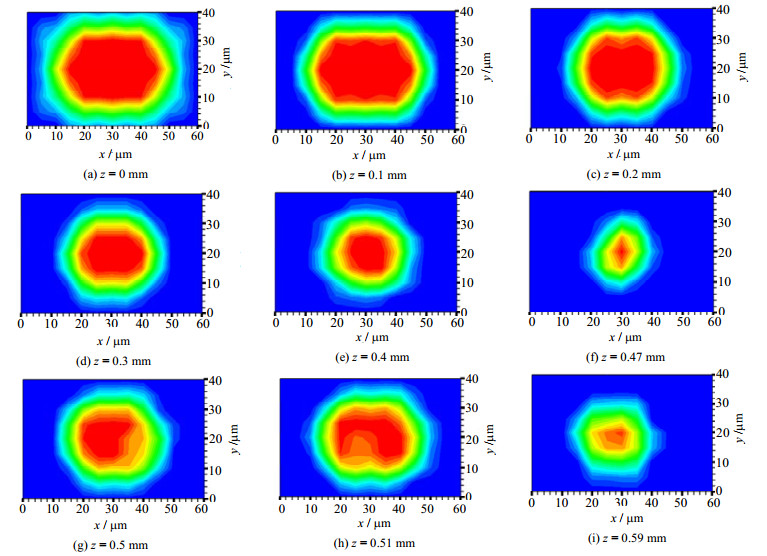
4 模拟结果与分析 4.1 凝结段通道截面气液相分布如图 5、6和7所示,沿着矩形通道周向,凝结液与气芯之间的气液界面存在曲率差异,在表面张力的作用下凝结液内部产生横向压力梯度,驱使凝结液流向通道壁面拐角处,从而减薄通道壁面中部附近的液膜厚度。随着气相在流动中不断凝结,通道截面气芯面积不断减小,同时气液界面的曲率差异不断减小,直至呈现光滑圆形。图 5(d)和5(e)显示液膜波动导致的通道截面气芯面积变化。图 5、6和7展示了矩形通道喷射流区域气液相分布规律:液桥逐渐生长并挤压气芯,使得通道截面气芯面积不断减小;环状流尾部气弹迅速增大,并呈现半球形。
|
图 5 a = b = 50 μm矩形通道截面气液相分布 Fig.5 Gas-liquid distribution on cross sections in the rectangular microchannel with a = b = 50 μm |
|
图 6 a = 40 μm, b = 50 μm矩形通道截面气液相分布 Fig.6 Gas-liquid distribution on cross sections in the rectangular microchannel with a = 40 μm and b = 50 μm |
|
图 7 a = 60 μm, b = 40 μm矩形通道截面气液相分布 Fig.7 Gas-liquid distribution on cross sections in the rectangular microchannel with a = 60 μm and b = 40 μm |
图 5、6和7同时显示通道宽高比对通道截面气液相分布影响较大:与方形通道相比,严格矩形通道截面周向液膜厚度差异更大;在环状流区域内需要更长的凝结长度才能使得通道截面气液界面呈现光滑圆形。这是因为严格矩形通道造成的气液界面曲率差异更大,在表面张力的作用下凝结液内部产生的横向压力梯度更大,致使凝结液在严格矩形通道截面短边上大量堆积,截面长边上的液膜相对较薄。
气弹周期性脱离、环状流尾部收缩、气液两相与液体间歇流过通道,使壁面剪切力与压力场发生变化,这导致环状流气液界面出现微幅波动。当气液界面剪切力足以克服毛细力时,微幅波动不断增长。
方形微通道内出现环波状流,而严格矩形微通道内没有出现环状流区域的气液界面波动,这说明严格矩形宽高比能显著影响气液界面波动。原因为:界面波动的产生需要一定厚度的凝结液,矩形微通道短边上集聚大量凝结液,但气液界面曲率半径与方形微通道相比更小,产生的毛细力更大,因此更能克服气液界面剪切力,进而抑制气液界面微幅波动生长。
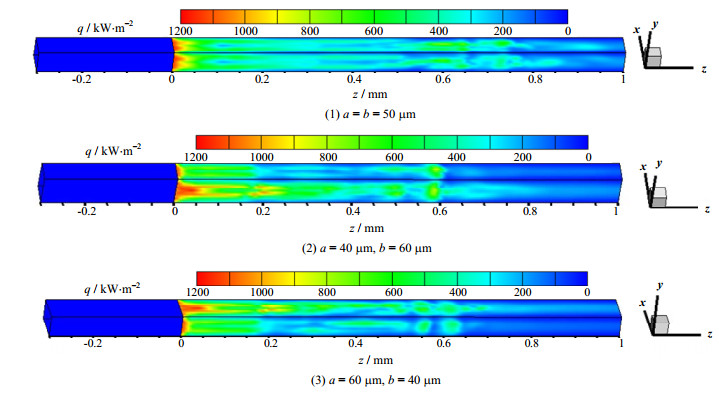
4.2 通道壁面热流密度分布图 8显示三种矩形微通道壁面热流密度分布规律,负号表示凝结放热。在等壁温凝结段(0≤z≤1 mm),气相沿着流动方向不断凝结,总体上液膜厚度逐渐增大,壁面热流密度逐渐减小。但在环状流波动区、喷射流和泡状流区域,液膜厚度处于动态变化状态,壁面热流密度发生振荡,出现局部增大的现象。
|
图 8 三种矩形微通道壁面热流密度分布 Fig.8 Wall heat flux distribution of the three rectangular microchannels |
Gregorig效应是指与圆形通道相比,非圆形通道截面气液界面存在曲率差异,在表面张力的作用下凝结液内部产生横向压力梯度,致使截面周向液膜厚度不一致,从而强化换热。与方形通道相比,严格矩形通道截面周向液膜厚度差异更大,导致严格矩形通道的Gregorig效应更强,即通道截面液膜厚度更不均匀,进而强化流动凝结换热(如图 8所示),这使得严格矩形通道有效凝结段平均壁面热流密度高于方形微通道。
4.3 矩形宽高比对喷射流的影响由图 3可知,等壁温凝结段(0≤z≤1 mm)内,随着气相在流动中持续凝结,总体上气芯速度不断减小。环状流尾部气芯与液膜的速度差很小,与惯性力相比,表面张力主导流动形态。在表面张力的作用下,尾部气芯趋于半球形,使自身表面势能趋于最小。半球状尾部气芯直径约等于通道水力直径,液膜流动被堵塞,导致液桥出现并逐渐生长。同时,液桥处气芯收缩并急剧加速,液桥处界面黏性力不断增大。当界面黏性力足以克服表面张力时,液桥合并,气泡在界面黏性力的作用下脱离环状气芯,泡状流形成。
忽略重力,作用在气液两相流中的压力、黏性力、表面张力和惯性力决定流动形态。气相所受惯性力与表面张力的相对大小由气相Weber数表示
| $ W{e_{\rm{v}}} = \frac{{{G^2}{D_{\rm{h}}}{x^2}}}{{\sigma {\rho _{\rm{v}}}}} $ | (22) |
式中,x为干度;Dh为水力直径,m。由于凝结减速,环状流尾部气芯的Wev减小至临界值,此时与惯性力相比,表面张力主导尾部气芯流动形态,喷射流发生。液桥处界面黏性力与表面张力的相对大小由气相Capillary数表示
| $ C{a_{\rm{v}}} = \frac{{{\mu _{\rm{v}}}Gx}}{{\sigma {\rho _{\rm{v}}}}} $ | (23) |
由于收缩加速,液桥处气芯的Cav增大至临界值。此时界面黏性力足以克服表面张力,使气弹脱离环状气芯。液桥处气芯的Cav越大,喷射流发生频率越高。
与方行通道相比,严格矩形通道内喷射流发生点向进口移动,即流型转换提前进行,并伴随更小的喷射流发生频率。其中方行通道喷射周期为0.12 ms,长边直立矩形通道喷射周期为0.23 ms,短边直立矩形通道喷射周期为0.21 ms。这是因为与方行通道相比,严格矩形通道的Gregorig效应更强,在环状流区域Z向相同位置上,严格矩形通道内气液两相流干度更小,导致该处气芯的Wev更小,于是喷射流发生点向进口移动,并伴随更小的液桥处气芯的Cav,即更小的喷射流发生频率。
5 结论基于VOF模型,建立了模拟矩形微通道内流动凝结的三维瞬态数值模型,速度进口采用分相模型,并考虑速度与液膜厚度的进口段效应,研究了宽高比对矩形微通道内R32流动凝结换热特性的影响规律,得到以下结论:
(1) 与方形微通道相比,严格矩形通道造成的气液界面曲率差异更大,在表面张力的作用下凝结液内部产生的横向压力梯度更大,致使凝结液在严格矩形通道截面分布更不均匀。
(2) 严格矩形通道有效凝结段平均壁面热流密度高于方形微通道。即当矩形宽高比偏离1:1,通道截面液膜分布不均匀性增加,Gregorig效应增强,进而强化换热。
(3) 与方形微通道相比,严格矩形微通道更有利于抑制气液界面微幅波动生长。
(4) 与方形微通道相比,严格矩形微通道内喷射流提前出现,并伴随更低的气弹脱离频率。这是由换热强化使得环状流尾部气芯的Wev和Cav减小导致的。
|
|
| [1] | Cheng P, Wu H Y. Mesoscale and microscale phase-change heat transfer[J]. Advances in Heat Transfer, 2006, 39: 461-563. DOI:10.1016/S0065-2717(06)39005-3. |
| [2] | Corimnne P, Jumana B, Christian S, et al. Analytic modeling, optimization, and realization of cooling devices in silicon technology[J]. IEEE Transactions on Components and Packaging Technologies, 2000, 23(4): 665-672. DOI:10.1109/6144.888851. |
| [3] | Cormac E, Tara D, Mark D, et al. Direct comparison between five different microchannels, part 1:channel manufacture and measurement[J]. Heat Transfer Engineering, 2005, 26(3): 79-88. DOI:10.1080/01457630590907392. |
| [4] | Zhang W, Xu J, Liu G. Multi-channel effect of condensation flow in a micro triple-channel condenser[J]. International Journal of Multiphase Flow, 2008, 34(12): 1175-1184. DOI:10.1016/j.ijmultiphaseflow.2008.05.004. |
| [5] | Zhang W, Xu J, Thome J R. Periodic bubble emission and appearance of an ordered bubble sequence (train) during condensation in a single microchannel[J]. International Journal of Heat and Mass Transfer, 2008, 51(13-14): 3420-3433. DOI:10.1016/j.ijheatmasstransfer.2007.11.025. |
| [6] | Chen Y, Wu R, Shi M H, et al. Visualization study of steam condensation in triangular microchannels[J]. International Journal of Heat and Mass Transfer, 2009, 52(21): 5122-5129. |
| [7] | Wu J F, Shi M H, Chen Y, et al. Visualization study of steam condensation in wide rectangular silicon microchannels[J]. International Journal of Thermal Sciences, 2010, 49(6): 922-930. DOI:10.1016/j.ijthermalsci.2010.01.007. |
| [8] | Fang C, David M, Wang F M, et al. Influence of film thickness and cross-sectional geometry on hydrophilic microchannel condensation[J]. International Journal of Multiphase Flow, 2010, 36(8): 608-619. DOI:10.1016/j.ijmultiphaseflow.2010.04.005. |
| [9] | Ma X, Fan X, Lan Z, et al. Flow patterns and transition characteristics for steam condensation in silicon microchannels[J]. Journal of Micromechanics and Microengineering, 2011, 21(7): 075009. DOI:10.1088/0960-1317/21/7/075009. |
| [10] | Quan X J, Cheng P, Wu H Y. Transition from annular flow to plug/slug flow in condensation of steam in microchannels[J]. International Journal of Heat and Mass Transfer, 2008, 51(3-4): 707-716. DOI:10.1016/j.ijheatmasstransfer.2007.04.022. |
| [11] | Wang H S, Rose J W, Honda H. A theoretical model of film condensation in square section horizontal microchannels[J]. Chemical Engineering Research and Design, 2004, 82(4): 430-434. DOI:10.1205/026387604323050137. |
| [12] | Wang H S, Rose J W. A theory of film condensation in horizontal noncircular section microchannels[J]. Journal of Heat Transfer, 2005, 127(10): 1096-1105. DOI:10.1115/1.2033905. |
| [13] | Wang H S, Rose J W. Film condensation in horizontal microchannels:effect of channel shape[J]. International Journal of Thermal Sciences, 2006, 45(12): 1205-1212. DOI:10.1016/j.ijthermalsci.2006.03.004. |
| [14] | Wang H S, Rose J W. Theory of heat transfer during condensation in microchannels[J]. International Journal of Heat and Mass Transfer, 2011, 54(11-12): 2525-2534. DOI:10.1016/j.ijheatmasstransfer.2011.02.009. |
| [15] | Wu J F, Chen Y, Shi M H, et al. Three-dimensional numerical simulation for annular condensation in rectangular microchannels[J]. Nanoscale and Microscale Thermophysical Engineering, 2009, 13(1): 13-29. DOI:10.1080/15567260802625882. |
| [16] | Hao T T, Ma X.H, Lan Z, et al. Analysis of the transition from laminar annular flow to intermittent flow of steam condensation in noncircular microchannels[J]. International Journal of Heat and Mass Transfer, 2013, 66: 745-756. DOI:10.1016/j.ijheatmasstransfer.2013.07.072. |
| [17] | Mghari E H, Asbik M, Louahlia G, et al. Condensation heat transfer enhancement in a horizontal non-circular microchannel[J]. Applied Thermal Engineering, 2014, 64(1-2): 358-370. DOI:10.1016/j.applthermaleng.2013.12.003. |
| [18] | Ganapathy H, Shooshtari A, Choo K, et al. Volume of fluid-based numerical modeling of condensation heat transfer and fluid flow characteristics in microchannels[J]. International Journal of Heat and Mass Transfer, 2013, 65: 62-72. DOI:10.1016/j.ijheatmasstransfer.2013.05.044. |
| [19] | Brackbill J U, Kothe D B, Zemach C. A continuum method for modeling surface tension[J]. Journal of Computational Physics, 1992, 100(2): 335-354. DOI:10.1016/0021-9991(92)90240-Y. |
| [20] | Lee W H. A pressure iteration scheme for two-phase flow modeling:vol.1[M].Washington, DC: Hemisphere Publishing, 1980. |