1 前言

间歇过程作为现代工业过程中极其重要的一种生产方式，已经被广泛应用于医药、食品、生物化工、半导体等多品种、高附加值产品的生产中^[1]。但是在实际过程中，由于设备老化和外在环境突变等一系列问题，故障时有发生。因此，对间歇过程进行故障监测对于保证生产过程的安全以及提高产品质量变得至关重要^[2]。

多路主成分分析(MPCA)和多路偏最小二乘(MPLS)通过将三维历史数据首先展开为二维矩阵再使用主成分分析(PCA)或偏最小二乘(PLS)方法对得到的二维矩阵进行分析，在间歇过程的故障监测领域得到广泛的应用^[3-5]。然而，由于工业过程变量绝大多数是非线性的，而PLS假设监测数据是线性的，因此不能很好地满足于工业实践。为了解决这个问题，Rosipal等^[6]将核技巧与PLS结合提出了一种核PLS(KPLS)算法，该算法可以有效解决监测数据的非线性问题^[7-8]。但是传统的基于KPLS的监测方法是对整个过程建立全局模型，而对于多阶段时变的间歇过程^[9]，建立单一的全局模型通常难以精确描述动态过程的变化特性。因此，将整个运行过程划分为多个阶段区域，再在每个区域内建立局部模型显得尤为重要。过程在不断变化，模型需要不断地更新来适应过程的变化，从而才能更准确地分析新样本。为了建立局部模型，即时学习(just-in-time-learning，JITL)策略近期被提出并被广泛应用于过程建模和监控^[10-11]。已有学者在局部建模方面做出了贡献，Liu等^[12]提出即时递推核学习(just-in-time kernel learning)方法，通过构造累积相似度因子，选择相似的样本集建立核学习辨识模型，但是，根据数据样本间的空间欧氏距离和角度信息来选择学习集，而忽略了数据的时间特性；Chen等^[13]提出一种应用遗忘因子以降低在线JITL选择数据量的方法，Hu等^[14-16]采用一系列滑动窗以及自适应相似性度量改进传统JITL，尽管这些方法可以减小模型的计算负担，但是，这些方法有可能使部分历史数据丢失，而且遗忘因子或者窗口宽度的调整也存在问题。

在基于即时学习^[17-18]的建模方法中，最为关键的是用以建立局部模型的学习集的选取。传统的即时学习算法一般根据数据样本间的空间欧氏距离和角度信息选择学习集，而不考虑数据的时间特性，因此当有异常数据出现时，就可能出现模型偏移的问题，同时，在进行局部建模时，对每个工作点都重新进行局部建模，建模计算量较大，耗时较长，模型输出的即时性也会受到影响。针对以上2个问题，本文提出一种分步的时空即时学习算法：首先，采用仿射传播(affinity propagation, AP)聚类^[19]用于分析经过展开及标准化的历史数据，计算出相对能够代表普通历史数据的聚类中心。在线监测阶段，计算采集到的当前时刻的数据与聚类中心的关系，并对历史数据进行初步筛选；之后用融入时间特性^[20]的时空JITL方法从这些初步筛选的数据中进一步进行精选以取得更精确的历史数据；最后，采用(multiway kernel partial least square, MKPLS)算法与选择的这些数据建立局部模型，并对当前的过程进行实时监测。

2 多向核偏最小二乘法

PLS作为一种分析输入变量空间和输出变量空间的相互关系多元回归算法^[21-22]，能够很好地将线性数据间的潜在特征提取出来，但是当这些数据是非线性时，由于PLS的固有线性，很难显示出优越性。为了解决非线性问题，核方法被引入到PLS算法中，它通过构造一个投影f将原始空间中的数据投影到高维空间降低数据整体的非线性。

$f:{{\mathit{\boldsymbol{x}}_i}} \in {{\mathbf{R}}^n}\left( {i = 1, 2, \cdot \cdot \cdot , I} \right)\xrightarrow{{}}\mathit{\boldsymbol{f}}\left( {{{\mathit{\boldsymbol{x}}_i}}} \right) \in \mathit{\boldsymbol{F}}$

(1)

式中：${{\mathit{\boldsymbol{x}}_i}}$为第i行输入数据，${{\mathbf{R}}^n}$为n维实数空间，F为高维特征空间，$\mathit{\boldsymbol{f}}\left( {{{\mathit{\boldsymbol{x}}_i}}} \right)$为输入数据映射到特征空间的非线性映射函数。假设$I \times M$维矩阵$\mathit{\boldsymbol{f}}\left( {{{\mathit{\boldsymbol{x}}_i}}} \right)$表示$\left\{ {{{\mathit{\boldsymbol{x}}_i}}} \right\}_{i = 1}^I$映射到F空间后的矩阵，M代表特征空间的维数，通过引入核方法，$\mathit{\boldsymbol{f}}{\left( {{{\mathit{\boldsymbol{x}}_i}}} \right)^T}\mathit{\boldsymbol{f}}\left( {{{\mathit{\boldsymbol{x}}_j}}} \right) = \mathit{\boldsymbol{K}}\left( {{{\mathit{\boldsymbol{x}}_i}}, {{\mathit{\boldsymbol{x}}_j}}} \right)$，其中K为$I \times I$维核矩阵。

输出数据的预测值为

$\hat{\boldsymbol{Y}}=\boldsymbol{K} \boldsymbol{U}\left(\boldsymbol{T}^{\mathrm{T}} \boldsymbol{K} \boldsymbol{U}\right)^{-1} \boldsymbol{T}^{\mathrm{T}} \boldsymbol{Y}$

(2)

式中：$\boldsymbol{U} = \left[ {{u_1}, {u_2}, \cdot \cdot \cdot , {u_C}} \right]$为输出数据Y的得分矩阵，$\boldsymbol{T} = \left[ {{t_1}, {t_2}, \cdot \cdot \cdot , {t_C}} \right]$为高维数据的得分矩阵，C为保留的隐变量的个数，虽然不知道f的显示表达，但矩阵T可表示为

$\boldsymbol{T}=\boldsymbol{K} \boldsymbol{U}\left(\boldsymbol{T}^{\mathrm{T}} \boldsymbol{K} \boldsymbol{U}\right)^{-1}$

(3)

此外，在建立KPLS模型之前，通常还需要对核矩阵K进行中心化处理。

由于间歇过程数据本身有批次数、变量数和采样数(时间数)3个维度，需要将原始的三维数据展开为二维数据进行建模，X(I×J×K)为正常工况下的间歇过程历史数据构成的三维矩阵，其中I为生产批次个数，J为观测变量个数，K为采样数。本文采用一种基于变量方向的展开方式，展开成$X\left( {I \times K \times J} \right)$的矩阵，相当于$I \times K$个J维的数据组成的矩阵。具体展开步骤为将后一批次的第一个数据接在前一批次最后一个数据后面，组成沿时间轴上的样本点；这种算法能够保留过程变量的维数，能够较好地、快速地检测故障或扰动。将三维数据展开成二维数据后再利用KPLS算法进行建模，即得到适合处理间歇过程三维数据的多向核偏最小二乘法(MKPLS)。

3 分步时空JITL局部样本筛选 3.1 分步历史数据样本筛选策略

分布历史数据样本选择策略的思想是保持模型精确度与一般算法处在相同水平的前提下，降低计算量需求，保留对全部历史数据进行筛选的可能性。在传统JITL方法应用的阶段，需要对历史数据中每一个样本进行相似度的计算，然而这样的计算在一个具有n个数据样本的历史数据中需要进行n次。所提出的方法可以分为3步，即离线准备阶段、初步在线筛选阶段、在线精选阶段。首先，离线准备阶段需要利用AP聚类方法取得历史样本的聚类中心，以供在线阶段使用；第2步，对新采集到的当前样本向量同初步筛选阶段得到的聚类中心计算新的隶属关系。最后，一个相关子数据集被选择出来，并进行在线精选之后这一组更小规模的数据会被用于局部的KPLS建模过程当中。这种方法寻找共同的基准点，从传统的大量的互为相对基准点计算转变为对有限个独立基准点进行的计算，从与全部历史样本进行对比到只与几个样本进行对比，因而在一定程度上可以减小算法的计算时间。

AP聚类是基于数据点间的“信息传递”的一种聚类算法，最大的优势是不需要在运行算法之前人为指定聚类的个数，而经典的K-means方法、模糊C均值(fuzzy c-means，FCM)方法都需要依据经验事先人为指定聚类个数，带有明显的人为因素，因而聚类的结果并不能保证真实有效，也无法反映实际生产过程的阶段特性。AP聚类算法将全部样本点看作网络的节点，自动地找寻具有代表性的聚类中心，使得所有样本点到最近的类代表点的相似度之和最大^[23]。

AP算法定义了吸引度信息矩阵R和归属度信息矩阵A: r(i, k)表示从i到k的消息，描述的是样本对象k适合作为样本对象i的聚类中心的程度；相反地，a(i, k)表示从k到i的消息，描述的是样本对象i选择样本对象k作为其据聚类中心的适合程度。AP算法进行交替2个信息传递的步骤，以更新2个矩阵。

首先，吸引信息r_t+1(i, k)按照式(4)迭代。

${r_{t + 1}}\left( {i, k} \right) = s\left( {i, k} \right) - \mathop {\max }\limits_{k' \ne k} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left\{ {{a_t}\left( {i, k'} \right) + s\left( {i, k'} \right)} \right\}$

(4)

式中：$s\left( {i, k} \right)$为样本点i和k之间的相似度，通过欧氏距离计算。${a_t}\left( {i, k'} \right)$为样本点$k'$到i的消息，$s\left( {i, k'} \right)$为样本点i和$k'$之间的相似度。然后，归属信息a_t+1(i, k)按照式(5)和(6)迭代。

${a_{t + 1}}\left( {i, k} \right) = \min \left( {0, {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {r_t}\left( {k, k} \right) + \sum\limits_{i' \notin \left\{ {i, k} \right\}} {\max {\kern 1pt} {\kern 1pt} \left\{ {0, {r_t}\left( {i', k} \right)} \right\}} } \right), {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i \ne k$

(5)

${a_{t + 1}}\left( {k, k} \right) = \sum\limits_{i' \ne k} {\max \left\{ {0, {r_t}\left( {i', k} \right)} \right\}} $

(6)

式中：${r_t}\left( {i', k} \right)$为样本点$i'$到k的消息，r_t(k, k)为样本点k到k的消息。

在进行迭代时，如果迭代次数超过设定的最大值或者当聚类中心在若干次迭代中不发生改变时停止计算并确定类中心及各类的样本点。

3.2 时空JITL局部模型

JITL是一种局部建模思想，主要目的是从历史数据库中选取与当前数据对应的最相似的历史采样，而全局建模利用的是历史数据库中的全部数据。因而利用JITL策略选择相似样本建模，最大的优势是可以提高模型的精度。传统的即时学习策略在从包含历史信息的数据库中选择相似样本，并构造学习集时采用的是基于欧氏距离和角度信息的相似度计算方法，相似度大小可以直接反映出x_i和x_q的靠近程度，选择建模数据时按照相似度由大到小依次选取若干数据，如式(7)所示：

$\left\{ \begin{array}{l} D\left( {{{\mathit{\boldsymbol{x}}_i}}, {{\mathit{\boldsymbol{x}}_q}}} \right) = {\alpha _1}{{\rm{e}}^{ - d\left( {{{\mathit{\boldsymbol{x}}_i}}, {{\mathit{\boldsymbol{x}}_q}}} \right)}} + \left( {1 - {\alpha _1}} \right)\cos \left[ {\theta \left( {{{\mathit{\boldsymbol{x}}_i}}, {{\mathit{\boldsymbol{x}}_q}}} \right)} \right] \\ D\left( {{{\mathit{\boldsymbol{x}}_1}}, {{\mathit{\boldsymbol{x}}_q}}} \right) > D\left( {{{\mathit{\boldsymbol{x}}_2}}, {{\mathit{\boldsymbol{x}}_q}}} \right) > ... > D\left( {{{\mathit{\boldsymbol{x}}_k}}, {{\mathit{\boldsymbol{x}}_q}}} \right) \\ \end{array} \right.$

(7)

式中：α₁为加权因子，$d\left( {{{\mathit{\boldsymbol{x}}_i}}, {{\mathit{\boldsymbol{x}}_q}}} \right)$为x_i与x_q的距离，$\theta \left( {{{\mathit{\boldsymbol{x}}_i}}, {{\mathit{\boldsymbol{x}}_q}}} \right)$为其夹角大小，计算方法如式(8)所示

$\left\{ \begin{array}{l} d\left( {{{\mathit{\boldsymbol{x}}_i}}, {{\mathit{\boldsymbol{x}}_q}}} \right) = \sqrt {{{\left\| {{{\mathit{\boldsymbol{x}}_i}} - {{\mathit{\boldsymbol{x}}_q}}} \right\|}^2}} \\ \theta \left( {{{\mathit{\boldsymbol{x}}_i}}, {{\mathit{\boldsymbol{x}}_q}}} \right) = \arccos {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{\mathit{\boldsymbol{x}}_i}^T{{\mathit{\boldsymbol{x}}_q}}}}{{{{\left\| {{{\mathit{\boldsymbol{x}}_i}}} \right\|}^2}{{\left\| {{{\mathit{\boldsymbol{x}}_q}}} \right\|}^2}}} \\ \end{array} \right.$

(8)

传统的即时学习算法一般根据数据样本间的空间距离进行学习集的选择，而不考虑数据的时间特性。在间歇生产过程中，设备特性、生产状况等会随时间发生变化，导致测量的数据在时间维度上显示出差异，因此在选取学习集的时候有必要考虑数据的时间特性。因此本文借鉴牛大鹏等^[20]的方法将数据的时间特性加入即时学习算法的相似度计算公式中，用于局部模型的建立。

融入时间特性的即时学习需要确定时间权重，首先假定所选择的学习集的时间权向量为

$ \boldsymbol{W}={[{w}_{1}, w{}_{2}, \cdot \cdot \cdot , {w}_{n}]}^{T}，{\displaystyle \sum _{m=1}^{n}{w}_{m}=1}, {w}_{m}\in \left[0, 1\right]$

(9)

式中：${w_1}, w{}_2, \cdot \cdot \cdot , {w_n}$为样本的时间权重。

为了充分反映样本中权重包含的信息程度，定义一个时间权向量的熵I_w，如式(10)所示。熵是度量信息大小的一个指标。熵值越大，则数据所含信息量越小。时间权向量的熵反映了对样本的集结过程中权重包含信息的程度。

${I_{\rm{w}}} = - \sum\limits_{m = 1}^n {{w_m}\ln {w_m}} $

(10)

为了反映样本中不同时段数据的权重差异，定义一个时间度λ，取值在0到1之间，如式(11)所示。即λ=0.1时，表明越注重距离当前工作点较近的数据；当λ=0.5时，说明同样重视所有时期数据；当λ=0.9时，表明越注重远期的数据。

$\lambda = \sum\limits_{m = 1}^n {\frac{{n - m}}{{n - 1}}} {w_m}$

(11)

本文中时间度λ根据赋值规则选取，w的确定既要充分考虑主观的专家经验知识，也要兼顾时间样本点本身所包含的客观信息，所以w的确定可转化为式(12)所示的非线性规划问题。

$\begin{gathered} \max \left( { - \sum\limits_{m = 1}^n {{w_m}\ln {w_m}} } \right) \\ {\rm{s}}{\rm{.t}}{\rm{. }}\lambda = \sum\limits_{m = 1}^n {\frac{{n - m}}{{n - 1}}} {w_m} \\ \sum\limits_{m = 1}^n {{w_m}} = 1, {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {w_m} \in \left[ {0, 1} \right] \\ m = 1, 2, \cdot \cdot \cdot , n \\ \end{gathered} $

(12)

综上，基于时间和空间相结合的JITL学习集选取规则为

$\left\{ \begin{array}{l} D\left( {{{\mathit{\boldsymbol{x}}_i}}, {{\mathit{\boldsymbol{x}}_q}}} \right) = {\alpha _1}{{\rm{e}}^{ - {d_{\rm{w}}}\left( {{{\mathit{\boldsymbol{x}}_i}}, {{\mathit{\boldsymbol{x}}_q}}} \right)}} + \left( {1 - {\alpha _1}} \right){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \cos \left[ {\theta \left( {{{\mathit{\boldsymbol{x}}_i}}, {{\mathit{\boldsymbol{x}}_q}}} \right)} \right] \\ {d_{\rm{w}}}\left( {{{\mathit{\boldsymbol{x}}_i}}, {{\mathit{\boldsymbol{x}}_q}}} \right) = \frac{{d\left( {{{\mathit{\boldsymbol{x}}_i}}, {{\mathit{\boldsymbol{x}}_q}}} \right)}}{{d\left( {{{\mathit{\boldsymbol{x}}_i}}, {{\mathit{\boldsymbol{x}}_q}}} \right) + r{w_i}}} \\ \end{array} \right.$

(13)

式中：r为可以调节的参数。若输入样本x_q波动较小时可以选取较大的r值；反之，则可以选取较小的r值。

4 基于分步时空JITL-MKPLS的间歇过程故障监测

间歇过程的数据一般呈三维矩阵，本文针对间歇过程的数据特性选取一种基于分步时空JITL-MKPLS算法进行故障监测。在利用本文所提的分布时空JITL算法从历史样本选择出与在线样本相似的样本后，采用MKPLS算法对筛选出的样本进行建模，采用Hotelling的T²统计量和SPE统计量作为监测指标，判断在线样本点是否发生故障。T²统计量和SPE统计量定义如下：

$\mathbf{T}_{k}^{2}=\boldsymbol{t}_{\mathrm{new}, k} \boldsymbol{\varLambda}_{k}^{-1} \boldsymbol{t}_{k}^{\mathrm{T}} \sim \frac{A\left(n^{2}-1\right)}{n(n-A)} F_{A, n-A, \alpha}$

(14)

式中：${{\boldsymbol{t}}_{new, k}}$为新采集样本在k时刻的得分向量，t_k为样本在k时刻的得分向量，$\Lambda _k^{}$为对应时刻的得分矩阵的协方差矩阵，且T²的控制限服从F分布，A为保留的隐变量的个数，n为样本点数，$\alpha $为置信区间。

$\mathrm{SPE}_{k}=\boldsymbol{e}_{\mathrm{new}, k} \boldsymbol{e}_{\mathrm{new}, k}^{\mathrm{T}} $

(15)

$\boldsymbol{e}_{\mathrm{new}, k}=\boldsymbol{x}_{\mathrm{new}, k}\left(I-P_{k} P_{k}^{\mathrm{T}}\right)$

(16)

式中：${{\boldsymbol{x}}_{\mathrm{new}, k}}$为新批次k时刻的过程数据，P_k为负载矩阵，SPE统计量用于监测采样点偏离模型空间的残差信息，并服从加权${\chi ^{\rm{2}}}$分布，SPE的控制限通过它的近似分布来确定。

$\mathrm{SPE}_{k} \sim g_{k} \chi_{k, h, \alpha}^{2}$

(17)

${g_k} = {b_k}/2{a_k}$

(18)

${h_k} = 2a_k^2/{b_k}$

(19)

式中：g为权重系数，h为自由度，${a_k}$和${b_k}$分别为k时刻的均值和方差。

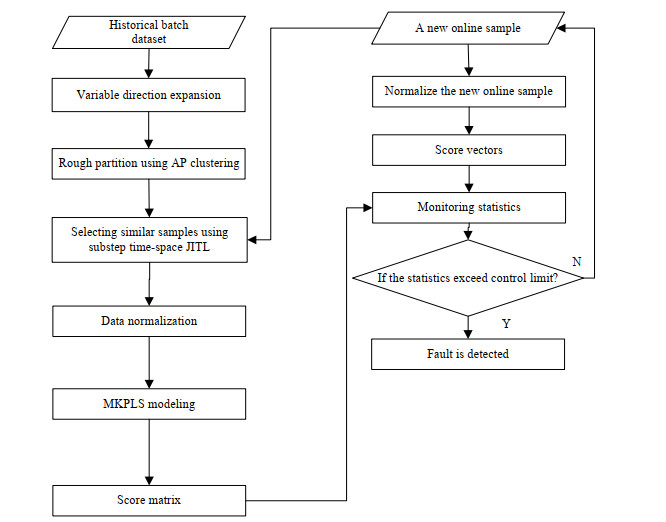
本文提出的基于分步时空JITL-MKPLS的间歇过程如图 1所示，具体建模步骤如下：

1) 历史批次数据采集，包括测量变量数据X和相应的已经测量得到的质量变量数据Y；

2) 将数据沿变量方向展开并进行标准化，记录方差与均值；

3) 对已得到的展开数据运用AP聚类算法，得到对应的聚类中心，聚类个数E；

4) 在线监控一新批次数据X_q，设当前新采样序号为k，利用相同的展开方式对该数据进行标准化处理，方差及均值则采用历史数据中的方差与均值；

5) 选择与X_q最相似的类作为初步建模数据X_fir；

6) 应用时空JITL策略计算X_q对应初步历史数据X_fir的相似度，精选出符合要求的第二步建模数据X_sec，其对应采样点的质量数据记为Y_sec；

7) 对所选的相似样本进行核计算，得到核矩阵K_i；

8) 将K_i和Y作为KPLS运算的输入，得到相应的得分矩阵T_i和U_i，计算监测模型的监测限；

9) 通过式(20)计算核向量$\boldsymbol{k}_{q} \in \mathbf{R}^{1 \times I}$：

$\left[\boldsymbol{k}_{q}\right]_{j}=\left\langle\boldsymbol{f}\left(\boldsymbol{x}_{q}\right), \boldsymbol{f}\left(\boldsymbol{x}_{j}\right)\right\rangle=\left[\boldsymbol{k}_{q}\left(\boldsymbol{x}_{q}, \boldsymbol{x}_{j}\right)\right]$

(20)

10) 对核向量k_q进行中心化和归一化：

$\tilde{\boldsymbol{k}}_{q}=\boldsymbol{k}_{q}-\mathbf{1}_{q} \boldsymbol{K}_{i}-\boldsymbol{k}_{q} \mathbf{1}_{I}+\mathbf{1}_{q} \boldsymbol{K}_{i} \mathbf{1}_{I}$

(21)

$\tilde{\boldsymbol{k}}_{q, \mathrm{scl}}=\frac{\tilde{\boldsymbol{k}}_{q}}{\operatorname{trace}\left(\boldsymbol{K}_{i}\right) /(I-1)}$

(22)

式中：1_q为值均为1/I的1×I维矩阵，1_I为值均为1/I的I×I维矩阵，K_i为平均中心核矩阵。

11) 对于新样本x_q，计算得分向量t_q：

$\boldsymbol{t}_{q}=\tilde{\boldsymbol{k}}_{q, \mathrm{scl}} \boldsymbol{U}_{i}\left(\boldsymbol{T}_{i}^{\mathrm{T}} \boldsymbol{K}_{i} \boldsymbol{U}_{i}\right)^{-1}$

(23)

式中：T_i为K_i对应的得分矩阵，U_i为Y对应的得分矩阵。

12) 计算在线样本的T²和SPE统计量，判断在线样本的统计量是否超限。

5 实验验证 5.1 青霉素发酵仿真实验

青霉素发酵过程是一个典型的动态、非线性、多相间歇过程。本文采用伊利诺伊理工学院开发的用于青霉素发酵的仿真平台进行实验，它可以对不同操作条件下青霉素生产过程的微生物浓度、CO₂浓度、pH值、青霉素浓度、氧浓度以及产生的热量等进行仿真。实验中每批的整个持续时间为400 h，采样间隔选择为1 h。为了检验该算法对故障监测的有效性，本文选择10个过程变量x₁、x₂、x₂、x₃、x₄、x₅、x₆、x₇、x₈、x₉、x₁₀和2个质量变量y₁、y₂构建统计模型，变量名称如表 1所示，设计了30批正常数据样本用于建模，一批额外正常数据和两批故障批次用于测试。其中选择30批正常数据的三维数据矩阵为X_30×10×400和Y_30×2×400。为了更接近实际生产状况，训练数据与测试数据均加入了1% 的噪声。该案例的计算机配置为64位Windows并带有8GB RAM和Intel(R) Core(TM) i5-3470 CPU，实验过程全程实时记录算法消耗的时间。

为了验证本文所提方法的有效性，本文选取正常样本、突变的阶跃故障和缓变的斜坡故障分别进行监测。通风速率和搅拌功率的变化会影响溶解氧浓度、温度等，最终会影响菌体浓度和青霉素的产物浓度，因此本实验选择了这2个变量进行故障设置，故障类型、幅值和持续时间如表 2所示。

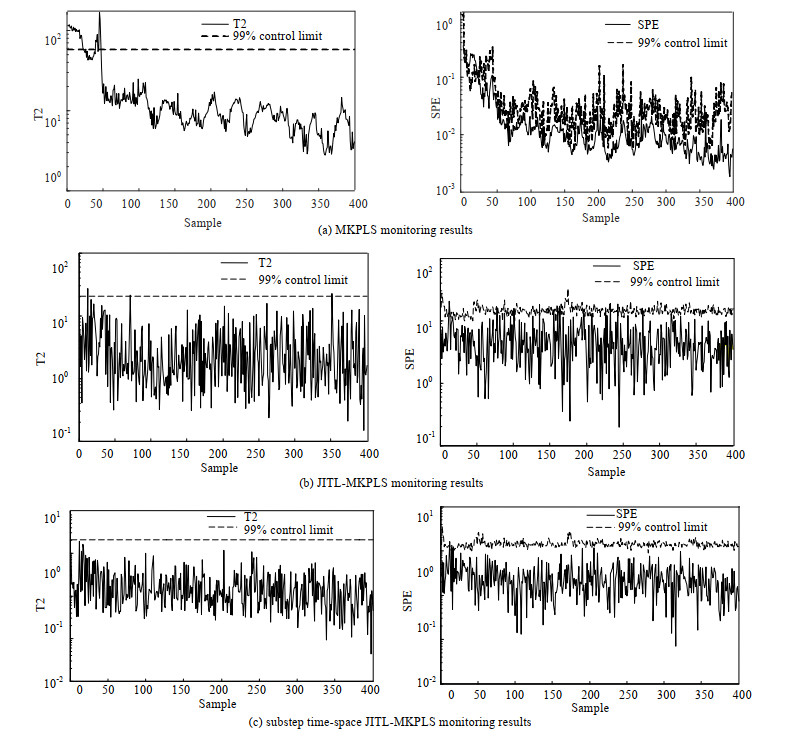
为了验证算法的有效性，本文与传统JITL-MKPLS进行对比，在本文所设置的实验中，初步样本筛选比率设置为10%，之后第2步精选过程中样本容量设置为10个采样点。AP聚类算法最终给出的聚类个数为3，分别为：(1-42)、(43-137)、(138-400)。如图 2所示为对正常批次生产过程的监测效果，其中虚线为99%控制限。从图 2中可以看出，加入即时学习思想的MKPLS算法要比传统的MKPLS算法监测效果好，因为发酵过程数据具有一定的阶段性和时变性，而即时学习是一种局部建模思想，因此可以弥补传统MKPLS建立全局模型的劣势。再对比图 2(a)和(c)，传统的JITL-MKPLS算法监测指标在整体上都接近控制限，在初始时刻及发酵后期都出现了误报，而本文所提的方法并没有出现误报现象。对比可以看出本文算法有更好的监控性能。因为在发酵过程中，生产状况会随着生产过程的进行而改变，采取融入时间特性的选取规格从数据库中选取数据集，可以使学习集的选取更加合理，从而提高建模的准确性。

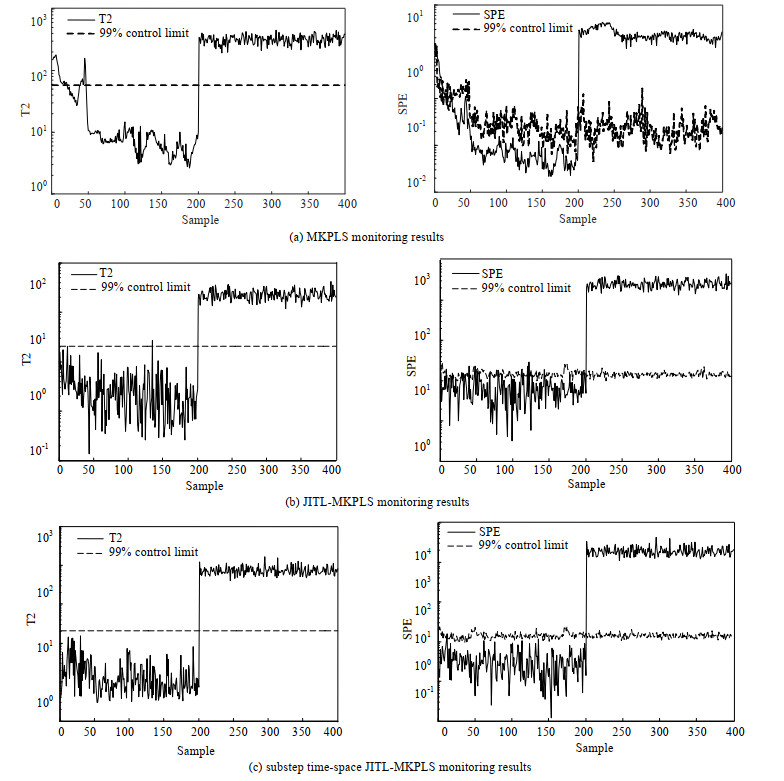
如图 3所示为模型在200时刻引入6% 的通风速率阶跃故障的监测结果图。如图 4所示为模型在100时刻引入2%的搅拌功率斜坡故障的监测结果图，从图中可以看出，采用同时考虑空间和时间的JITL策略所建立的模型比传统的MKPLS和传统的JITL-MKPLS更加精准，能够更准确地进行故障监测。尤其在生产开始阶段，各项指标都不稳定时，本文所提出的方法误报率都为0，在出现故障后，监测到故障的时间也比传统方法更短。同时，由于采用了分步样本筛选方法，所建立的模型在保证精度的前提下，计算时间也大大地缩短，详细指标如表 3所示。

5.2 大肠杆菌发酵现场实验

大肠杆菌发酵过程的在线监测实验数据是在工厂的真实生产环境中产生的，真实生产过程存在着人为操作等诸多不确定因素，对于算法研究更具有现实意义。

本次实验选用的大肠杆菌发酵数据来源于北京某生物制药厂。发酵时间为6~7 h。由于实际数据批次之间的差异，每批数据选取有72个采样点。本实验选择了7个过程变量与一个质量变量OD值构建统计模型，变量名称如表 4所示。

为了验证本文所提方法的有效性，本文选取10批正常数据建立历史样本库，并分别用1批正常数据和2批故障数据进行测试，故障类型、幅度和持续时间如表 5所示。其中选择10批正常数据的三维数据矩阵为X_10×7×72和Y_10×1×72。

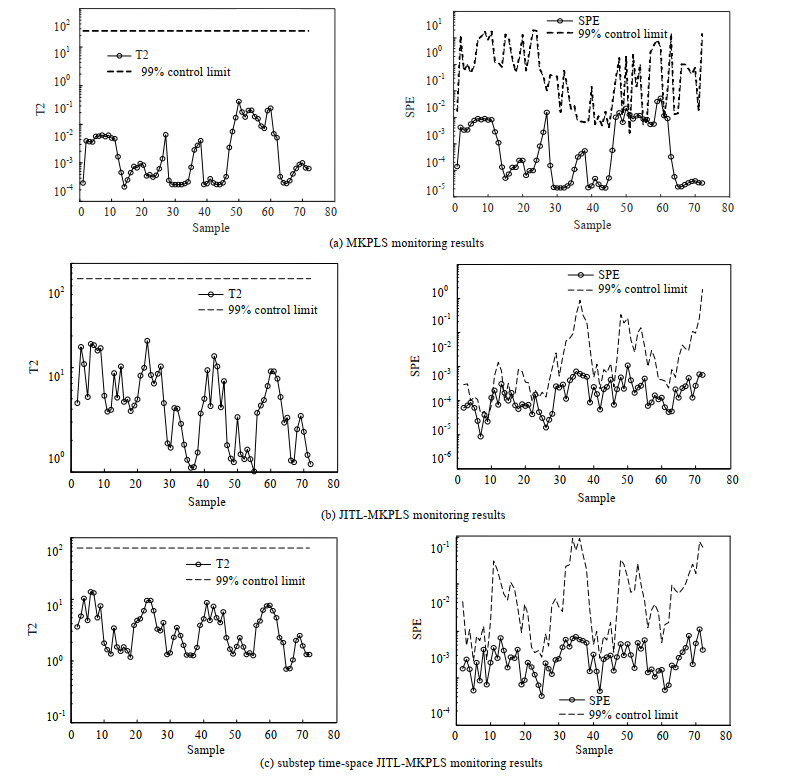
为了验证算法的有效性，本文与传统MKPLS和JITL-MKPLS进行对比，在本文所设置的实验中，初步样本筛选比率设置为10%，之后第2步精选过程中样本容量设置为5个采样点。AP聚类算法最终给出的聚类个数为3，分别为：(1-10)、(11-34)、(35-72)。如图 5所示为对正常批次生产过程的监测效果，其中虚线为99% 控制限，从图 5(b)中可以看出，2种方法的T²对正常样本都没有误报，但传统方法的SPE有7个时刻出现误报，本文方法只在前期一个时刻发生了误报。这是因为本文在相似样本选择时同时考虑了样本的时间和空间特性使得所建模型更加准确。

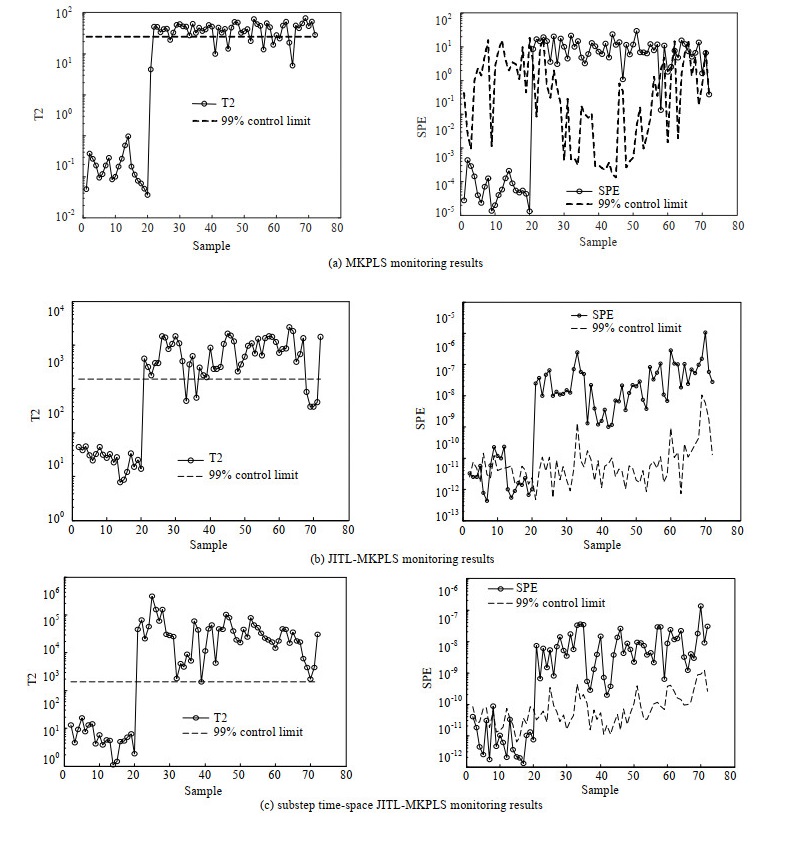
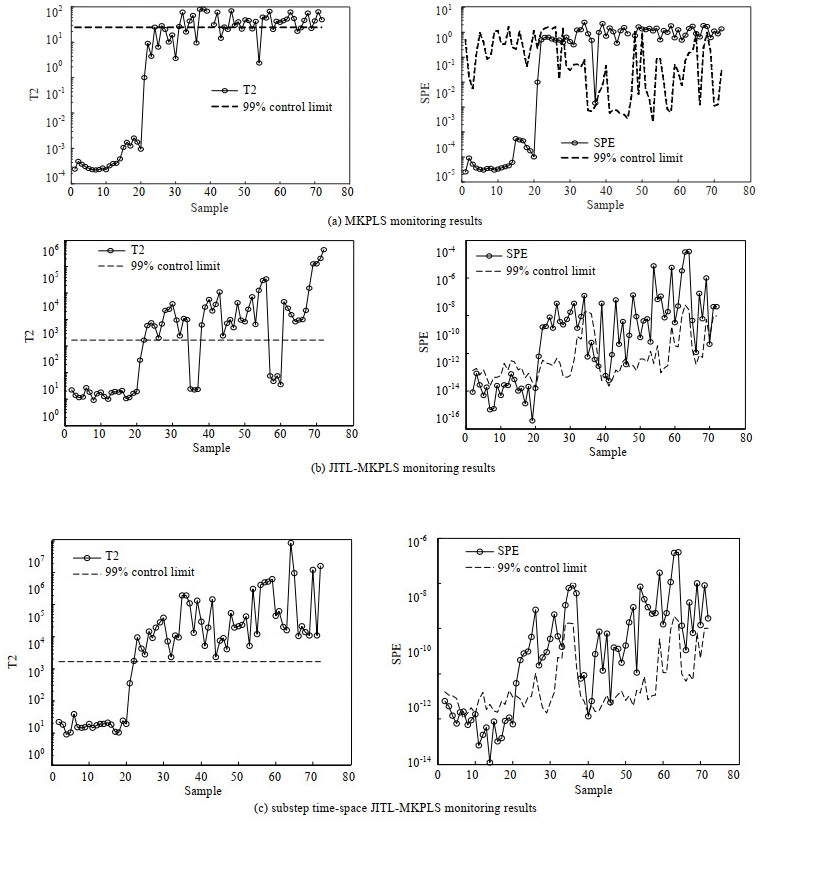
阶跃故障为突发故障，一般幅值也比较大，如图 6所示为模型在第21时刻引入的通风速率阶跃故障的监测结果图，如图 7所示为模型在第21时刻引入的搅拌功率斜坡故障的监测结果图，从图中可以看出，采用同时考虑空间和时间的JITL策略所建立的模型更加精准，能够更准确地进行故障监测。本文所提出的方法误报率都为0，在出现故障后，监测到故障的时间也比传统方法更短。同时，由于采用了分步样本筛选方法，所建立的模型在保证精度的前提下，算法运行时间也大大地缩短。详细指标如表 6所示。

6 结语

本文针对传统JITL-MKPLS遇到的在线计算压力大问题，提出了分步样本筛选策略，首先通过AP聚类的方法对数据样本集中的数据进行粗分类，在当前输入样本数据到达后，先确定当前样本数据所属的类别，再在此类别所限定的子数据样本集中使用JITL策略确定出局部模型，减少不必要的计算量，节约监测时间。同时将时间特性融入JITL方法中，提高了所建模型的准确性和实时性，最后通过和不引入JITL策略、传统的JITL策略进行比较，本文提出的方法不仅能够表征时变系统当前状态，节约监测时间，而且有较低的误报率和漏报率。