醇、水流体常作为工业原料广泛应用于化学、化工等领域,其中甲醇、乙醇还可作为清洁燃料[1]、高性能换热器的工质[2]等用于节能减排,因此其热力学性质特别是比热容性质对工业设计、生产、储存等环节极为重要。状态方程是研究流体热物性的重要工具,甲醇、乙醇和水都已被构建可准确描述其热力学性质的亥姆霍兹专用方程,其中水的比热容平均绝对相对偏差(以下简称偏差)低于0.2%[3],乙醇低于2%[4],甲醇低于3%[5],但方程形式较为复杂,不适合工业应用。立方型方程形式简单、通用性强[6-9],在工业中应用较多,如化工模拟软件Aspen Plus,但对醇、水这类强极性缔合流体的计算精度较差,如SRK(Soave-Redlich-Kwong)方程对水的液相比体积偏差为25%,比热容偏差高于15%[10]。Kontogeogis等[11-12]将SRK方程与缔合理论相结合提出立方型附加缔合项(CPA)状态方程(EoS),可以准确计算缔合流体的相平衡和密度性质[13],同时具有相对简单的形式,但对比热容计算精度不高。CPA方程的参数一般通过蒸汽压和饱和液相密度拟合得到,采用该参数计算方法Zhu等[14]发现CPA方程对二氧化碳的比热容计算精度较差,液相比热容偏差最高达23.38%,Liang等[15]通过计算水的性质发现CPA方程对定容及比定压热容性质的计算偏差均高于5%,Lundstrøm等[10]发现在273~373 K,方程对水比定压热容偏差高于6.6%。可见在确定CPA方程参数时采用传统方法对比热容的计算精度不高。Kang等[16]在对氢氟烯烃(HFOs)类物质CPA方程构建中发现,参数计算中加入比定压热容后方程对该性质的计算精度提高,总体偏差由3.1% 降至1.6%。针对传统的CPA方程构建方法对比热容计算精度不高的问题,本研究借鉴Kang等[16]的思路,在方程构建中考虑不同的热力学性质,研究CPA方程对甲醇、乙醇、水3种极性缔合流体的比热容性质的计算能力。
2 CPA状态方程模型及参数计算方法研究采用Kontogeorgis等[12]简化后的CPA方程,方程由SRK方程和缔合项构成,形式如下:
| $ p = \frac{{{R_{\text{m}}}T}}{{{V_{\text{m}}} - b}} - \frac{{\alpha (T)}}{{{V_{\text{m}}}({V_{\text{m}}} + b)}} - \frac{1}{2}\frac{{{R_{\text{m}}}T}}{{{V_{\text{m}}}}}\left( {1 + {\rho _{\text{m}}}\frac{{\partial \ln g}}{{\partial {\rho _{\text{m}}}}}} \right)\sum\limits_{\text{A}} {(1 - {X_{\text{A}}}} ) $ | (1) |
其中:
| $ \alpha (T) = {a_0}{\left[ {1 + {c_1}\left( {1 - \sqrt {T/{T_{\text{c}}}} } \right)} \right]^2} $ | (2) |
| $ {X_{\text{A}}}{\text{ = }}\frac{1}{{1{\text{ + }}{\rho _{\text{m}}}\sum\limits_{\text{B}} {{X_{\text{B}}}{\Delta ^{{\text{AB}}}}} }} $ | (3) |
其中ΔAB表达式如下:
| $ {\Delta ^{{\text{AB}}}}{\text{ = }}g({\rho _{\text{m}}})\left[ {{{\exp }_{}}({{{\varepsilon ^{{\text{AB}}}}} \mathord{\left/ {\vphantom {{{\varepsilon ^{{\text{AB}}}}} {({R_{\text{m}}}T)) - 1}}} \right. } {({R_{\text{m}}}T)) - 1}}} \right]b{\beta ^{{\text{AB}}}} $ | (4) |
径向分布函数g的公式如下:
| $ {\text{ }}g({\rho _{\text{m}}}){\text{ = }}\frac{1}{{1 - 1.9n}} $ | (5) |
其中n=(1/4)bρm。
CPA方程的比热容性质可以通过剩余亥姆霍兹自由能导出,计算公式如下:
| $ {c_{V,{\text{m}}}} = - T\left( {\frac{{{\partial ^2}A_{\text{m}}^{{\text{res}}}}}{{\partial {T^2}}}} \right) + c_{p,{\text{m}}}^{{\text{ig}}} - {R_{\text{m}}} $ | (6) |
| $ {c_{p,{\text{m}}}} = {c_{V,{\text{m}}}} - T\frac{{\left( {{{\partial p} \mathord{\left/ {\vphantom {{\partial p} {\partial T}}} \right. } {\partial T}}} \right)_V^2}}{{{{\left( {{{\partial p} \mathord{\left/ {\vphantom {{\partial p} {\partial V}}} \right. } {\partial V}}} \right)}_T}}} $ | (7) |
CPA的剩余亥姆霍兹自由能由SRK项和缔合项组成,表达式如下:
| $ A_{{\text{m,CPA}}}^{{\text{res}}} = A_{{\text{m,SRK}}}^{{\text{res}}} + A_{{\text{m,assoc}}}^{{\text{res}}} $ | (8) |
SRK方程和缔合项的剩余亥姆霍兹自由能由Michelsen等[17-18]给出,表达式如下:
| $ A_{{\text{m,SRK}}}^{{\text{res}}} = - {R_{\text{m}}}T{\ln _{}}\left( {1 - {\rho _{\text{m}}}b} \right) - \frac{\alpha }{b}{\ln _{}}\left( {1 + {\rho _{\text{m}}}b} \right) $ | (9) |
| $ A_{{\text{m,assoc}}}^{{\text{res}}} = {R_{\text{m}}}T\sum\limits_{\text{A}} {\left( {\ln {X_{\text{A}}} - \frac{{{X_{\text{A}}}}}{2} + \frac{1}{2}} \right)} $ | (10) |
CPA方程中需要计算的参数共有5个:a0、b、c1、εAB、βAB,目标函数的形式如下:
| $ {\text{OF}} = \sum\limits_{i = 1}^{{N_{\text{P}}}} {\sum\limits_{j = 1}^N {\left[ {{{\left( {\frac{{U_j^{\exp } - U_j^{{\text{cal}}}}}{{U_j^{\exp }}}} \right)}^2}} \right]} } $ | (11) |
热力学性质U包括蒸汽压psat、饱和液相密度ρm'、饱和气相密度ρm"、单相密度ρmall以及气、液相比定压热容(
为了研究比热容在CPA方程构建中的影响,本研究采用包含不同热力学性质的参数计算方法见表 1。表 1中的拟合方法根据是否考虑比热容分为两组。第1组:方法1、2和3,这3种方法在参数计算过程中不考虑比热容性质,用于研究CPA方程对不同比热容的预测能力。其中方法1考虑蒸汽压、饱和气液相密度,方法2在方法1的基础上考虑气液相密度性质,方法3相对方法2不考虑蒸汽压性质。第2组:方法4~11,在参数计算过程中考虑不同比热容,用于研究加入比热容对CPA方程计算精度的影响,除方法10,其余方法均包含所有的非比热容性质,其中方法4、5只考虑比定压热容;方法6、7只考虑液相或气相的比热容;方法8、9只考虑定压或比定容热容;方法10、11考虑所有比热容。
|
|
表 1 不同参数计算方法的目标函数组合 Table 1 Objective function combinations of different parameter estimation methods |
CPA方程对不同性质的计算精度通过平均绝对相对偏差AARD确定,其定义如下:
| $ {\text{AARD = }}\frac{{{\text{100}}}}{N} \times \sum\limits_i^N {\left| {\frac{{U_i^{\exp } - U_i^{{\text{cal}}}}}{{U_i^{\exp }}}} \right|} $ | (12) |
本研究的CPA方程参数计算使用美国国家标准与技术研究院(NIST)[19]提供的饱和及单相数据,计算温度范围:230~500 K(甲醇、乙醇),280~550 K(水);计算压力范围:< 7×106 Pa。参考Folas等[13],本研究甲醇、乙醇的缔合类型为2B型,水的缔合类型为4C型。3种物质的参数计算结果如表 2所示。
|
|
表 2 甲醇、乙醇、水不同参数计算方法的计算结果 Table 2 Calculation results of different parameter estimation for methanol, ethanol and water |
第1组:对比3种物质方法1和2的偏差结果可以看出,不考虑单相密度性质对蒸汽压及密度的计算精度影响较小,两方法偏差的平均值AVEa几乎不变。对比方法1、2与3的结果可以看出,在计算过程中不考虑蒸汽压会造成3种物质的蒸汽压的精度大幅降低,且会对液相比热容的计算精度影响较大,其中对水的影响最为明显,蒸汽压的偏差增大了约300倍,液相比定压热容的偏差增大了约26倍,而气相比定压热容偏差仅增大了约1倍,且蒸汽压偏差增大,液相比热容的偏差也会增大。由上述分析可知蒸汽压的精度会影响比热容的预测精度,并对液相比热容表现出一定的规律性。对比3种方法的比热容计算结果可以看出,CPA方程对3种物质比热容的计算偏差均大于3%,其中水的计算结果相对较好,甲醇的相对较差。在该组方法中方法1考虑的性质较少,且蒸汽压及密度的计算精度与方法2差别很小,因此在不考虑比热容性质时更推荐方法1。由上述分析可知,不考虑比热容时,CPA方程在参数计算过程中须考虑蒸汽压性质,且蒸汽压的计算精度越高,方程对液相比热容的预测精度越高,但最低的偏差仍有3.25%,方程对比热容的计算精度仍不高。
第2组:从考虑全部比热容的方法10和11的计算结果可以看出,CPA方程对3种物质的比热容的计算偏差均在3% 以上,这说明方程并不能同时准确计算所有比热容性质。从2种方法计算结果可以看出,饱和密度对比热容的影响不大。
从方法8和9的比热容计算结果可以看出,对3种物质,CPA方程都无法准确计算气液相的定压或比定容热容,其中对水而言,2种方法都在计算液相比热容时取得较高精度,方法8中液相比定压热容偏差为1.22%,方法9中液相比定容热容的计算偏差为2.45%。
从方法6和7的计算结果来看,方法6中甲醇、乙醇、水的液相定容、比定压热容偏差之和分别为5.63%、5.16%、7.34%,方法7中气相比热容偏差之和分别为35.66%、10.45%、7.94%。这表明,相比气相方程参数,计算中考虑液相比热容可以得到更高的计算精度,方程对液相比热容的计算能力强于气相。
综合两组方法在排除方法3、4和5后,每种比热容考虑总次数相同。从各比热容偏差的平均值AVEb可以看出,CPA方程对4种比热容的计算精度并不相同,对这3种缔合流体,液相比定压热容的计算精度都要高于其他比热容,最小偏差分别为1.86%、2.53%、1.22%。从各物质的AVEb可以看出CPA方程很难准确计算甲醇的气相比热容(偏差的平均值大于20%),对液相比热容性质计算偏差的平均值也是3种物质中最大的,而水的偏差在3种物质中最小。但水用方法5及7计算结果显示,即使只考虑气相比热容,CPA方程对该性质的计算偏差仍然无法降低至3% 以内。综上所述,CPA方程适合计算3种流体液相比定压热容,并可以取得较高的计算精度。
从方法4~11与方法2得出的密度和蒸汽压的偏差的平均值AVEa可以看出,考虑比热容后,方程对蒸汽压和密度的整体计算精度降低,但方法4的降低幅度较小。通过方法4构建的CPA方程结果可以看出,在参数计算时只考虑液相比定压热容、蒸汽压及密度性质时,对于蒸汽压和密度,水的计算偏差均低于1%,甲醇、乙醇除了饱和气相密度偏差在3% 及以内,其他均低于2%;对于液相比定压热容,水、甲醇的计算偏差在2% 以内,乙醇在3% 以内。因此,CPA方程能在保证蒸汽压和密度性质的计算精度较高的情况下,可较准确地描述物质液相比定压热容。且在第2组方法中,方法4在对3种物质的液相比定压热容、蒸汽压和密度性质的计算偏差和最小。
采用方法1和4计算出的CPA状态方程参数值见表 3。图 1~3比较了各个物质用方法1与4得出的液相比定压热容及蒸汽压的计算值与文献值。
|
|
表 3 3种物质的方法1及方法4的CPA方程参数 Table 3 CPA parameters of method 1 and method 4 for the three substances |
|
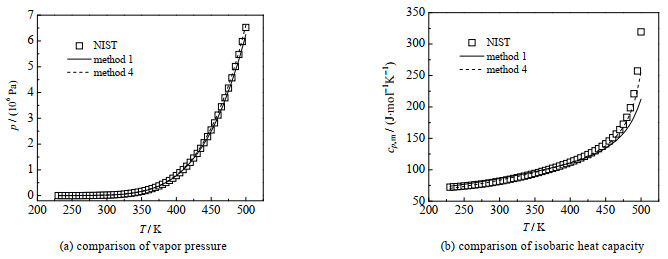
图 1 方法1及方法4对甲醇的蒸汽压和液相比定压热容计算结果 Fig.1 Calculation results of methanol vapor pressure and isobaric heat capacity in liquid phase by methods 1 and 4 |
|
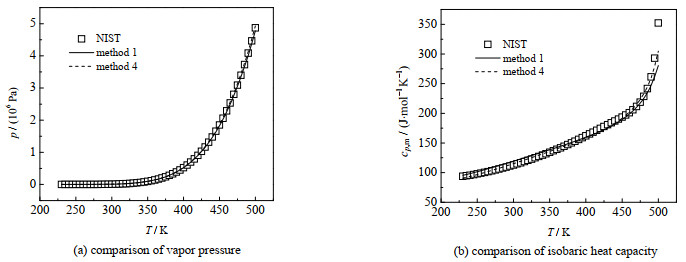
图 2 方法1及方法4对乙醇的蒸汽压及液相比定压热容计算结果 Fig.2 Calculation results of ethanol vapor pressure and isobaric heat capacity in liquid phase by methods 1 and 4 |
|
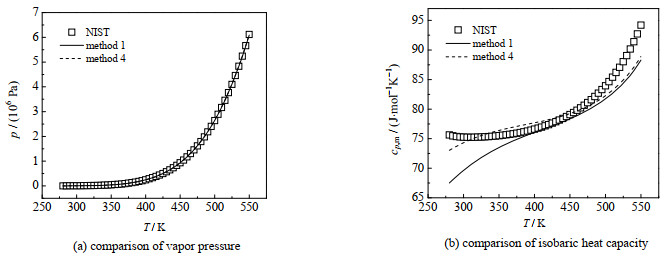
图 3 方法1及方法4对水的蒸汽压及液相定压比热容计算结果 Fig.3 Calculation results of water vapor pressure and isobaric heat capacity in liquid phase by methods 1 and 4 |
从图 1~3中的(a)可以看出方法1和4对3种物质的蒸汽压的计算精度差别不大,水和乙醇用2种方法的蒸汽压的曲线几乎重合,甲醇在温度高于450 K时,2种方法的计算精度有一定区别。
从图 1和2中的(b)可以看出,在温度高于470 K时,甲醇和乙醇的液相比热容的变化率随着温度的升高而增大,CPA方程的计算精度逐渐降低。在温度小于470 K时,CPA状态方程对这2种物质的液相比定压热容的计算精度较高,方法1与4对液相比定压热容的计算精度差别不大,方法4稍好。
从图 3(b)可以看出,对水来说,2种方法的液相比定压热容曲线在温度高于400 K时计算偏差相差不大,而在温度低于400 K时,方法4要明显好于方法1,但2种方法的变化趋势和实验数据不一致。
综上所述,方法1与4对3种物质的蒸汽压计算精度相差不大,对液相比热容的计算精度在某个温度区间相差较大,方法4的计算值更接近文献值,计算精度更高。
4 结论通过包含不同性质的参数计算方法研究了CPA方程对缔合流体甲醇、乙醇及水比热容的计算,主要结论如下:参数计算中不考虑比热容性质时,蒸汽压精度对液相比热容影响较大,比热容精度较低;考虑比热容后,方程仅对液相比定压热容有较高的计算精度;仅考虑液相比热容(方法4),可以在保证蒸汽压、密度高精度的同时提高液相比定压热容的精度。因此方法4可作为CPA方程参数计算方法,提高液相比定压热容的计算精度。
符号说明:
AARD ⎯ 平均绝对相对偏差
α ⎯ 能量项
Am ⎯ 亥姆霍兹自由能,J·mol−1
βAB ⎯ 缔合体积参数
a0 ⎯ 能量项α的参数,Pa·m6·mol−2
ΔAB ⎯ 缔合强度,m3·mol−1
b ⎯ 协体积参数
εAB ⎯ 缔合能量参数,Pa·m3·mol−1
c1 ⎯ 能量项α的参数,修正a0所用的系数
ρm ⎯ 摩尔密度,mol·m−3
cV, m ⎯ 摩尔比定容热容,J·mol−1·K
上、下标
cp, m ⎯ 摩尔比定压热容,J·mol−1·K
all ⎯ 气相和液相
g ⎯ 径向分布函数
assoc ⎯ 缔合项
N ⎯ 实验数据点数
cal ⎯ 计算值
NP ⎯ 热力学性质个数
exp ⎯ 文献值
OF ⎯ 目标函数
gas ⎯ 气相
p ⎯ 压力,Pa
i, j ⎯ 自然数1,2,3,…
Rm ⎯ 通用气体常数,J·mol−1·K−1
ig ⎯ 理想气体
T ⎯ 温度,K
liq ⎯ 液相
Tc ⎯ 临界温度,K
res ⎯ 剩余项
U ⎯ 热力学性质
sat ⎯ 饱和状态
Vm ⎯ 摩尔体积,m3·mol−1
' ⎯ 饱和液相
XA ⎯ 分子的缔合点位A不能成键的分子分率
" ⎯ 饱和气相
XB ⎯ 分子的缔合点位B不能成键的分子分率
| [1] |
张凡, 王建海, 王小臣, 等. 醇类汽油车醇醛酮、芳香烃和烯烃类排放的试验研究[J]. 环境科学, 2013, 34(7): 2539-2545. ZHANG F, WANG J H, WANG X C, et al. Experimental research on alcohols, aldehydes, aromatic hydrocarbons and olefins emissions from alcohols fuelled vehicles[J]. Environmental Science, 2013, 34(7): 2539-2545. |
| [2] |
BASTAKOTI D, 张红娜, 李凤臣. 不同工质时脉动热管换热特性实验研究[J]. 工程热物理学报, 2017, 38(7): 1454-1458. BASTAKOTI D, ZHANG H N, LI F C. An experimental study on thermal performance of pulsating heat pipe with different working fluids[J]. Journal of Engineering Thermophysics, 2017, 38(7): 1454-1458. |
| [3] |
WAGNER W, PRUß A. The IAPWS formulation 1995 for the thermodynamic properties of ordinary water substance for general and scientific use[J]. Journal of Physical and Chemical Reference Data, 2002, 31(2): 387-535. DOI:10.1063/1.1461829 |
| [4] |
ESTELA-URIBE J F. Fundamental multiparameter and association equation of state for ethanol[J]. Fluid Phase Equilibria, 2017, 452: 74-93. DOI:10.1016/j.fluid.2017.08.018 |
| [5] |
KUME D, SAKODA N, UEMATSU M. An equation of state for thermodynamic properties for methanol[J]. Journal of Chemical & Engineering Data, 2005, 28(2): 1-32. |
| [6] |
相华江, 张军, 葛众, 等. 基于PR方程多元混合工质相平衡性质研究[J]. 热能动力工程, 2020, 35(4): 169-173, 193. XIANG H J, ZHANG J, GE Z, et al. Study on phase equilibrium properties of multi-component mixtures based on PR equation[J]. Journal of Engineering for Thermal Energy and Power, 2020, 35(4): 169-173, 193. |
| [7] |
郝敏, 陈保东. RKS方程在天然气热物性计算中的应用[J]. 油气储运, 2003, 22(10): 22-27. HAO M, CHEN B D. The application of RKS equation in calculating thermo-physical properties of natural gas[J]. Oil & Gas Storage and Transportation, 2003, 22(10): 22-27. |
| [8] |
李春喜, 宋红艳. 用SRK状态方程计算二氧化碳在N—甲基二乙醇胺水溶液中的溶解度[J]. 高校化学工程学报, 2000, 14(4): 373-377. LI C X, SONG H Y. Solubility calculation of carbon dioxide in MDEA aqueous with SRK equation of state[J]. Journal of Chemical Engineering of Chinese Universities, 2000, 14(4): 373-377. |
| [9] |
李思广, 李彦军, 杨龙滨, 等. 基于不同状态方程预测气体水合物相平衡条件[J]. 化工学报, 2018, 69(增刊1): 8-14. LI S G, LI Y J, YANG L B, et al. Prediction of phase equilibrium of gas hydrates based on different equations of state[J]. CIESC Journal, 2018, 69(Suppl.1): 8-14. |
| [10] |
LUNDSTRØM C, MICHELSEN M L, KONTOGEORGIS G M, et al. Comparison of the SRK and CPA equations of state for physical properties of water and methanol[J]. Fluid Phase Equilibria, 2006, 247(1/2): 149-157. |
| [11] |
KONTOGEORGIS G M, VOUTSAS E C, YAKOUMIS I V, et al. An equation of state for associating fluids[J]. Industrial & Engineering Chemistry Research, 1996, 35(11): 4310-4318. |
| [12] |
KONTOGEORGIS G M, YAKOUMIS I V, MEIJER H, et al. Multicomponent phase equilibrium calculations for water-methanol-alkane mixtures[J]. Fluid Phase Equilibria, 1999, 158/159/160: 201-209. |
| [13] |
FOLAS G K, GABRIELSEN J, MICHELSEN M L, et al. Application of the cubic-plus-association (CPA) equation of state to cross-associating systems[J]. Industrial & Engineering Chemistry Research, 2005, 44(10): 3823-3833. |
| [14] |
ZHU C Y, LIU X Y, XUE S, et al. A comprehensive study on thermophysical properties of carbon dioxide through the cubic-plus-association and crossover cubic-plus-association equations of state[J]. Journal of Chemical & Engineering Data, 2020, 65(9): 4268-4284. |
| [15] |
LIANG X D, TSIVINTZELIS I, KONTOGEORGIS G M. Modeling water containing systems with the simplified PC-SAFT and CPA equations of state[J]. Industrial & Engineering Chemistry Research, 2014, 53(37): 14493-14507. |
| [16] |
KANG K, WANG X P, KONTOGEORGIS G M, et al. Modeling hydrofluoroolefins with the cubic plus association and perturbed-chain statistical associating fluid theory equations of state[J]. Industrial & Engineering Chemistry Research, 2018, 57(50): 17289-17300. |
| [17] |
MOLLERUP J M, MICHELSEN M L. Calculation of thermodynamic equilibrium properties[J]. Fluid Phase Equilibria, 1992, 74: 1-15. |
| [18] |
MICHELSEN M L, HENDRIKS E M. Physical properties from association models[J]. Fluid Phase Equilibria, 2001, 180(1/2): 165-174. |
| [19] |
LEMMON E W, BELL I H, HUBER M L, et al. NIST standard reference database 23: Reference fluid thermos-dynamic and transport properties-REFPROP, version 10.0 [DB]. Gaithersburg: National Institute of Standards and Technology, 2018.
|




