利福平(rifampicin),化学名3-[[(4-甲基-1-哌嗪基)亚氨基]甲基]-利福霉素,分子式C43H58N4O12,分子量为822.97,是半合成利福霉素类抗生素的一种,临床上主要用于治疗肺结核和麻风病等[1]。因其具有广谱抗菌作用、毒副作用小、疗效高等特点,目前越来越多地制作为复合药剂应用于其他疾病的治疗,例如心内膜炎、耐药性伤寒和呼吸道感染等,市场需求稳中有升,因此利福平生产技术和质量的进步具有现实意义[2]。
利福平复杂的分子结构使得其存在多种晶型及溶剂化物,与结晶系统使用的溶剂密切相关[3]。利福平的药用晶型为Ⅰ和Ⅱ晶型,Ⅰ晶型在正丁醇中重结晶获得[4],Ⅱ晶型在丙酮中重结晶获得[5]。两种晶型在堆密度、溶出速率、粒径、热稳定性等方面有所不同,在一定条件下可以发生溶剂介导转晶和固体转晶相互转化。在工业生产中,无论采用正丁醇还是丙酮作为结晶溶剂,体系中都残留有前端工序带来的正丁醇溶剂组分,且在丙酮中结晶时,为追求大粒径产品,而添加少量水,因此都不能得到形貌完整的Ⅰ或Ⅱ晶型晶体,常是以混晶形式存在。而相关研究往往只关注了两种晶型在纯溶剂中的热力学数据,并未探究在溶剂中长时间平衡过程中利福平晶型的转变[6],以及混合溶剂组成中的热力学数据。
本文研究Ⅰ晶型利福平在常用结晶溶剂中溶解时发生的晶型转变。系统测定在不同温度下Ⅱ晶型利福平在正丁醇-丙酮和水-丙酮两种混合溶剂体系中的溶解度,并采用多种经验方程对溶解度数据进行拟合。研究结果能够为利福平生产工艺优化和产品质量控制提供基础数据。
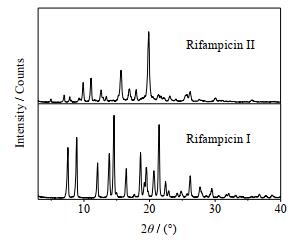
2 实验部分 2.1 试剂与仪器Ⅰ晶型和Ⅱ晶型利福平,上海新铂化学技术有限公司,经高效液相色谱仪检测,纯度98.030%。经粉末X射线衍射法(powder X-ray diffraction,PXRD)检测,结果如图 1所示,在13.6°和14.4°检测到Ⅰ晶型的特征峰,在9.9°和11.1°检测到Ⅱ晶型的特征峰,原料分别为Ⅰ晶型和Ⅱ晶型利福平[7]。正丁醇、丙酮均为分析纯,由上海泰坦科技股份有限公司提供;去离子水,实验室自制。
|
图 1 Ⅰ和Ⅱ晶型利福平的PXRD特征图 Fig.1 PXRD pattern of rifampicin Ⅰ and Ⅱ |
BSA224S-CW型分析天平(精度(±0.000 1) g),赛多利斯科学仪器有限公司;DC-3015低温恒温槽(精度±0.1 ℃),上海恒平科学仪器有限公司;DZF-6020型真空干燥箱,上海精宏实验设备有限公司;D8 Advance型X射线衍射仪,布鲁克(北京)科技有限公司。
2.2 实验方法实验所用装置如图 2所示。将过量Ⅰ晶型利福平分别加入到正丁醇、丙酮、正丁醇-丙酮、水-丙酮混合溶剂中,在一定温度下恒温搅拌6 h以上,然后取底层沉淀做PXRD分析,确定晶型是否发生转变。

|
图 2 溶解度测定实验装置
Fig.2 Schematic diagram of the experimental setup for solubility measurements
1. low-temperature thermostatic bath 2. thermometer 3. condenser 4. jacketed vessel 5. magnetic stirrers |
测量溶解度数据的方法有平衡法[8-10]和动态法[11],本文采取平衡法。将适量溶剂加入到玻璃夹套瓶中,打开恒温水浴槽并调节至指定温度,然后用精度为0.1 K的温度计测量夹套瓶内体系温度,微调水浴槽温度,直至被测体系达到指定温度。当温度稳定后,加入过量的Ⅱ晶型利福平,搅拌6 h使夹套瓶内溶液达到固液平衡。关闭搅拌,在该温度下静置6 h以上,以保证固液分离,上层溶液中没有悬浮颗粒。然后吸取上层清液,并通过0.45 μm微滤膜过滤至洁净已称重的培养皿中,迅速称量培养皿和溶液的质量。将培养皿放入真空干燥箱中,干燥48 h以上,直至质量不再变化。
利福平在纯溶剂中的摩尔溶解度使用下式计算:
| $ {x_i} = \frac{{{m_1}/{M_1}}}{{{m_1}/{M_1} + {m_2}/{M_2}}} $ | (1) |
利福平在正丁醇-丙酮、水-丙酮混合溶剂中的摩尔溶解度使用下式计算:
| $ {x_i} = \frac{{{m_1}/{M_1}}}{{{m_1}/{M_1} + {m_2}/{M_2} + {m_3}/{M_3}}} $ | (2) |
其中,m1为溶质的质量(g);m2和m3为不同溶剂的质量(g);M1、M2和M3分别为溶质和不同溶剂的相对分子质量(g·mol-1)。
为确保溶解度测试数据的可靠性,实验时分别于搅拌4、6和12 h后取样分析,发现4 h后溶液浓度已经稳定不变,因此搅拌时间6 h足够保证固液溶解平衡。实验使用的溶剂易挥发,在实验装置上添加冷凝管,以保证溶剂的冷凝回流。每次实验重复3次以保证数据准确性。对底层晶体过滤、烘干后,使用PXRD检测,发现在实验过程中Ⅱ晶型利福平没有发生晶型转变。
为验证实验装置的可靠性,测量了不同温度下氯化钾在水中的溶解度,并将测量值与文献数据[12]比较,相对偏差在0.5%以内,说明实验装置与方法是可靠的,可用于Ⅱ晶型利福平溶解度的测定。
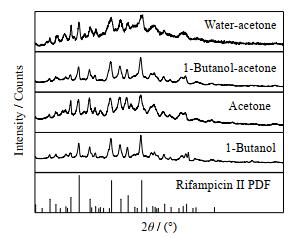
3 实验结果与分析 3.1 Ⅰ晶型利福平在溶剂中的晶型转变研究Ⅰ晶型在溶剂中的溶解度时,分析底物晶体的PXRD,如图 3所示。发现在正丁醇、丙酮、正丁醇-丙酮、水-丙酮溶剂中均发生了溶剂介导转晶,利福平从Ⅰ晶型转变为Ⅱ晶型。在Ⅰ晶型溶解平衡过程中,逐渐形成Ⅱ晶型的晶核,然后晶体生长消耗了溶液浓度,进而又促进原先Ⅰ晶型的溶解,这种晶型转变过程在一些多晶型药物中普遍存在[13]。所以不宜使用平衡法测量Ⅰ晶型利福平在上述溶剂中的溶解度数据。
|
图 3 Ⅰ晶型利福平在不同溶剂中的PXRD Fig.3 PXRD pattern of rifampicin form Ⅰ in different solvents |
实验测量了在288.15~323.15 K时Ⅱ晶型利福平在正丁醇-丙酮、水-丙酮混合溶剂中的溶解度,结果见表 1和2。
|
|
表 1 利福平在正丁醇-丙酮混合溶剂中的溶解度实验值与计算值 Table 1 Experimental and calculated values of rifampicin solubility in 1-butanol-acetone mixed solvents |
|
|
表 2 利福平在水-丙酮混合溶剂中的溶解度实验值与计算值 Table 2 Experimental and calculated values of rifampicin solubility in water-acetone mixed solvents |
Apelblat方程[14]越来越多用于溶解度数据的拟合,该模型假定溶液的焓变为温度的线性函数,经进一步简化、修订后可用于关联溶解度与温度之间的关系,方程形式如式(3):
| $ {\rm{ln}}{\kern 1pt} {\kern 1pt} x = A + B/T + C{\kern 1pt} {\rm{ln}}{\kern 1pt} {\kern 1pt} T $ | (3) |
理想状态方程[15]是根据热力学原理描述固液平衡状态的常用方程,方程形式如式(4):
| $ {\rm{ln}}{\kern 1pt} {\kern 1pt} x = a + b/T $ | (4) |
对于物质在二元混合溶剂中的固液平衡问题,本文选用ACREE等提出的(CNIBS)/Redlich-Kister方程[16],拟合利福平在正丁醇-丙酮、水-丙酮混合溶剂中的溶解度,方程形式如式(5):
| $ {\rm{ln}}{\kern 1pt} {\kern 1pt} x = {B_0} + {B_1}y + {B_2}{y^2} + {B_3}{y^3} + {B_4}{y^4} $ | (5) |
使用相对偏差(RD)、平均相对偏差(ARD)、均方根偏差(RMSD)检测实验结果和计算结果的一致性。各式计算公式如下:
| $ {{\rm{RD}} = \left| {\frac{{{x_i} - {x_{{\rm{cal}}}}}}{{{x_i}}}} \right|} $ | (6) |
| $ {{\rm{ARD}} = \frac{1}{N}\sum\limits_{i = 1}^N | \frac{{{x_i} - {x_{{\rm{cal}}}}}}{{{x_i}}}|} $ | (7) |
| $ {{\rm{RMSD}} = \left[ {\frac{{\sum\limits_{i = 1}^N {{{({x_i} - {x_{{\rm{cal}}}})}^2}} }}{N}} \right]} $ | (8) |
Ⅱ晶型利福平在不同配比的正丁醇-丙酮混合溶剂中的溶解度数据及不同模型计算值如表 1和图 4所示。从图中可以发现,利福平在不同配比的溶剂中,溶解度都随着温度升高而增大。当y1 = 1.000时,即溶剂为正丁醇时,利福平的溶解度最小。当y1 = 0.350时,利福平的溶解度最大。从图 5可以发现,在相同温度下,随着混合溶剂中正丁醇含量的增加,利福平的溶解度先迅速增大,达到最大值后,然后下降。这种变化趋势在高温时显著。低温时整体溶解度较低,变化不明显。其原因可能与分子间氢键有关,丙酮分子中存在羰基,形成氢键时羰基可作为氢键受体,但是分子内不存在氢键供体,在纯丙酮溶剂中,不形成氢键,所以丙酮易挥发,且黏度小。正丁醇分子中存在一个羟基,形成氢键时,既能作为氢键受体又能作为氢键供体,正丁醇分子间可以形成氢键,所以正丁醇相对丙酮挥发性小,黏度大。利福平分子结构复杂,分子内存在羟基、胺基、羰基等多种能形成氢键的基团。在丙酮中加入正丁醇,正丁醇中的羟基与利福平分子间形成氢键,使得溶解度增大。但当正丁醇含量增加,由于正丁醇分子间的氢键数量增加,使得利福平与正丁醇形成氢键减少,导致溶解度下降。

|
图 4 利福平在正丁醇-丙酮混合溶剂中的溶解度
Fig.4 Solubility of rifampicin in 1-butanol-acetone mixed solvents
■ y1 = 0.000 ○ y1 = 0.168 ▲ y1 = 0.350 ▽ y1 = 0.548 ◆ y1 = 0.763 y1 = 1.000 |

|
图 5 利福平在正丁醇-丙酮混合溶剂中的溶解度与溶剂组成关系
Fig.5 Relationship between solubility of rifampicin in 1-butanol-acetone
mixed solvents and composition of solvents
■ T = 288.15 K ○ T = 293.15 K ▲ T = 298.15 K ▽ T = 303.15 K ◆ T = 308.15 K ▽ T =313.15 K ▲ T = 318.15 K T =323.15 K |
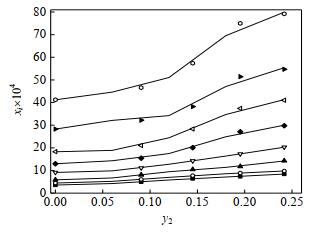
Ⅱ晶型利福平在不同配比的水-丙酮混合溶剂中的溶解度数据及不同模型计算值如表 2和图 6所示。从图中可以发现,利福平在不同配比溶剂中的溶解度随着温度升高而增大。从图 7可以发现,在同一温度下溶解度随着混合溶剂中水含量的增大而增大。其原因应该与正丁醇-丙酮体系类似,容易形成氢键的水分子,使得溶剂中与利福平形成的氢键增加,进而使得溶解度增大。

|
图 6 利福平在水-丙酮混合溶剂中的溶解度
Fig.6 Solubility of rifampicin in water-acetone mixed solvents
■ y2 = 0.000 ○ y2 = 0.091 ▲ y2 = 0.145 ▽ y2 = 0.195 ◆ y2 = 0.242 |
|
图 7 利福平在水-丙酮混合溶剂中的溶解度与溶剂组成关系
Fig.7 Relationship between solubility of rifampicin in water-acetone mixed solvents and composition of solvents
■ T = 288.15 K ○ T = 293.15 K ▲ T = 298.15 K ▽ T = 303.15 K ◆ T = 308.15 K ▽ T = 313.15 K ▲ T = 318.15 K T = 323.15 K |
分别采用Apelblat方程和理想状态方程拟合两个溶剂体系中的实验数据,结果见表 3。在正丁醇-丙酮溶剂中,两个方程的拟合R2均大于0.993,ARD分别小于5%、12%,最大RMSD分别为0.819×10-4和1.809×10-4,从整体结果上来看,Apelblat方程的拟合效果要优于理想状态方程。(CNIBS)/ Redlich-Kister方程的拟合结果见表 4,R2大于0.994,关联良好。在水-丙酮溶剂中,Apelblat方程和理想状态方程的拟合R2均大于0.994,ARD分别小于5%、10%,最大RMSD分别为0.858×10-4和1.246×10-4,同样Apelblat方程的拟合效果优于理想状态方程。(CNIBS)/Redlich-Kister方程的拟合R2大于0.999,关联良好。
|
|
表 3 Apelblat方程和理想状态方程模型参数回归结果 Table 3 Parameters of the Apelblat equation and ideal model |
|
|
表 4 (CNIBS)/Redlich-Kister方程模型参数回归结果 Table 4 Parameters of the (CNIBS)/Redlich-Kister equation and ideal model |
固液平衡体系的热力学参数可以通过修正的van’t Hoff方程来计算。在恒定压力下溶质的标准摩尔溶解焓计算公式如式(9)[17]:
| $ {\Delta _{{\rm{sol}}}}H_{\rm{m}}^{\rm{o}} = - R{\left( {\frac{{\partial {\kern 1pt} {\rm{ln}}{\kern 1pt} {\kern 1pt} {x_i}}}{{\partial (1/T - 1/{T_{\rm{m}}})}}} \right)_p} $ | (9) |
其中Tm为所有实验温度的平均值(本实验中Tm = 305.22 K),计算公式如式(10):
| $ {T_{\rm{m}}} = \frac{N}{{\sum\limits_{i = 1}^N 1 /{T_i}}} $ | (10) |
式中:N为实验数据的温度点数。
标准摩尔溶解吉布斯自由能和标准摩尔溶解熵计算公式如式(11)、(12):
| $ {{\Delta _{{\rm{sol}}}}G_{\rm{m}}^{\rm{o}} = - R{T_{\rm{m}}} \times {\rm{ intercept }}} $ | (11) |
| $ {{\Delta _{{\rm{sol}}}}S_{\rm{m}}^{\rm{o}} = \frac{{{\Delta _{{\rm{sol}}}}H_{\rm{m}}^{\rm{o}} - {\Delta _{{\rm{sol}}}}G_{\rm{m}}^{\rm{o}}}}{{{T_{\rm{m}}}}}} $ | (12) |
式中:intercept是以lnxi和(1/T -1/Tm)作图得出的截距。
溶解过程中焓变和熵变的贡献通过式(13)、(14)计算:
| $ {{\xi _{\rm{H}}}/\% = 100 \times \frac{{{\Delta _{{\rm{sol}}}}H_{\rm{m}}^{\rm{o}}}}{{|{\Delta _{{\rm{sol}}}}H_{\rm{m}}^{\rm{o}}| + |{T_{\rm{m}}}{\Delta _{{\rm{sol}}}}S_{\rm{m}}^{\rm{o}}}}} $ | (13) |
| $ {{\xi _{{\rm{TS}}}}/\% = 100 \times \frac{{|{T_{\rm{m}}}{\Delta _{{\rm{sol}}}}S_{\rm{m}}^{\rm{o}}|}}{{{\Delta _{{\rm{sol}}}}H_{\rm{m}}^{\rm{o}}}}| + |{T_{\rm{m}}}{\Delta _{{\rm{sol}}}}S_{\rm{m}}^{\rm{o}}} $ | (14) |
两种混合体系中的热力学计算结果如表 5所示。在两种体系中利福平ΔsolHmo和ΔsolGmo和Δsol均为正值,表明在这些体系的溶解为吸热过程,该结果与溶解度随着温度升高而增大相符合。此外根据van’t Hoff方程计算得到的吉布斯自由能为标准状态下的溶解吉布斯自由能,所以不能据此判断反应是否自发进行。ξH的计算结果均大于50%,说明在实验过程中ΔsolHmo和Δsol对ΔsolGmo的贡献较大。
|
|
表 5 利福平溶解热力学性质 Table 5 Thermodynamic properties of rifampicin solutions |
(1) Ⅰ晶型利福平在正丁醇、丙酮、正丁醇-丙酮、水-丙酮混合溶剂中发生溶剂介导转晶,转变为Ⅱ晶型,因此在这些溶剂中Ⅰ晶型的溶解度难以通过平衡法测量。
(2) 采用平衡法测定了288.15~323.15 K时Ⅱ晶型利福平在正丁醇-丙酮和水-丙酮混合溶剂体系中的溶解度。在所有体系中,溶解度随着温度升高而增大。使用Apelblat模型能够很好拟合溶解度数据,关联结果良好。
(3) 在正丁醇-丙酮体系中溶解度随着正丁醇的摩尔比增加先增大后减小,在摩尔比0.350附近溶解度最大。在水-丙酮体系中,溶解度随着水的摩尔比增加而增大。引入温度参数采用(CNIBS)/Redlich-Kister模型进行修正,结果显示关联良好,改善了模型单因素预测的缺陷,有效地提高了利福平在二元混合溶剂中溶解度的预测精度。
(4) 根据van’t Hoff方程计算了利福平在两种混合溶剂中的ΔsolHmo和Δsol、ΔsolGmo和Δsol和ΔsolSmo和Δsol。由结果可知,ΔsolHmo和Δsol均为正值,表明利福平在溶剂体系中的溶解均为吸热反应,溶解度值随着温度升高增大,实验值很好地符合这一结论。
符号说明:
|
|
| [1] |
HENWOOD S Q, DE VILLIERS M M, LIEBENBERG W, et al. Solubility and dissolution properties of generic rifampicin raw materials[J]. Drug Development and Industrial Pharmacy, 2000, 26(4): 403-408. DOI:10.1081/DDC-100101246 |
| [2] |
黄慧玲.给药途径及剂型因素对两种晶型利福平药动学的影响[D].天津: 天津大学, 2014. HUANG H L. Effects of delivery route and dosage form on the pharmacokinetics of two crystal forms of rifampicin [D]. Tianjin: Tianjin University, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10056-1015017351.htm |
| [3] |
兰静, 胡昌勤. 制剂中利福平晶型的确定[J]. 中国抗生素杂志, 2003, 28(6): 347-350. LAN J, HU C Q. Determination of rifampicin crystalline forms in preparation[J]. Chinese Journal of Antibiotics, 2003, 28(6): 347-350. DOI:10.3969/j.issn.1001-8689.2003.06.008 |
| [4] |
杨培明. 甲哌力复霉素Ⅰ型结晶的研制[J]. 抗生素, 1979(1): 20-30. YANG P M. Development of rifampicin form Ⅰ crystallization[J]. Chinese Journal of Antibiotics, 1979(1): 20-30. |
| [5] |
甲哌力复霉素生产工艺改革[J].中国抗生素杂志, 1978(2): 11-17. Reform of rifampicin production process [J]. Chinese Journal of Antibiotics, 1978(2): 11-17. http://www.cnki.com.cn/Article/CJFDTotal-ZKSS197802001.htm |
| [6] |
JING D, GU Y, XIA H. Solid-state and solution-mediated polymorphic transformation of rifampicin[J]. Chemical Engineering & Technology, 2018(6): 1-9. |
| [7] |
AGRAWAL S, ASHOKRAJ Y, BHARATAM P V, et al. Solid-state characterization of rifampicin samples and its biopharmaceutic relevance[J]. European Journal of Pharmaceutical Sciences, 2004, 22(2/3): 127-144. |
| [8] |
FANG W J, CHEN K, JI L J, et al. Solubility and thermodynamic properties of N-acetylglucosamine in mono-solvents and binary solvents at different temperatures[J]. Physics and Chemistry of Liquids, 2019, 57(5): 587-599. DOI:10.1080/00319104.2018.1506921 |
| [9] |
于玉振, 张晓慧, 李鹏坤, 等. 普瑞巴林晶型Ⅰ在纯溶剂及丙酮-水混合溶剂中的溶解度测定与关联[J]. 高校化学工程学报, 2017, 31(1): 7-12. YU Y Z, ZHANG X H, LI P K, et al. Measurement and correlation of Pregabalin form Ⅰ solubility in pure solvents and acetone-water mixtures[J]. Journal of Chemical Engineering of Chinese Universities, 2017, 31(1): 7-12. |
| [10] |
支娟娟, 徐家阔, 刘琼, 等. 喜树碱在二甲亚砜和甲醇(或乙醇)混合溶剂中溶解度的测定和关联[J]. 高校化学工程学报, 2016, 30(5): 999-1006. ZHI J J, XU J K, LIU Q, et al. Measurement and correlation of Camptothecine solubility in dimethylsulfoxide-methanol/ethanol mixed solvents[J]. Journal of Chemical Engineering of Chinese Universities, 2016, 30(5): 999-1006. DOI:10.3969/j.issn.1003-9015.2016.05.003 |
| [11] |
周彩荣, 石晓华, 冯伟, 等. 新戊二醇在溶剂中溶解度的测定及关联[J]. 高校化学工程学报, 2010, 24(3): 365-369. ZHOU C R, SHI X H, FENG W, et al. Measurement and correlation of solubilities of neopentyl glycol in solvents[J]. Journal of Chemical Engineering of Chinese Universities, 2010, 24(3): 365-369. DOI:10.3969/j.issn.1003-9015.2010.03.001 |
| [12] |
PINHO S P, MACEDO, EUGÉNIA A. Solubility of NaCl, NaBr, and KCl in water, methanol, ethanol, and their mixed solvents[J]. Journal of Chemical & Engineering Data, 2005, 50(1): 29-32. |
| [13] |
佟瑶.乙水杨胺-糖精的共结晶过程及其多晶型转化机理研究[D].天津: 天津大学, 2017. TONG Y. Study on cocrystallization process and polymorphic transformation mechanism of ethenzamide-saccharin cocrystal [D]. Tianjin: Tianjin University, 2017. http://cdmd.cnki.com.cn/Article/CDMD-10056-1018011566.htm |
| [14] |
APELBLAT A, MANZUROLA E. Solubilities of o-acetylsalicylic, 4-aminosalicylic, 3, 5-dinihdsalicylic, p-toluicacid and magnesium- D Laspartate in water from T = (278 to 348) K[J]. The Journal Chemical Thermodynamics, 1999, 31(10): 85-91. |
| [15] |
韩世钧. 化工相平衡[M]. 北京: 中国石化出版社, 1991. HAN S J. Chemical phase equilibrium[M]. Beijing: China Petrochemical Press, 1991. |
| [16] |
杨久利, 沙作良, 杨立斌, 等. 甘氨酸在丙酮-水混合溶剂中溶解度的测定与关联[J]. 高校化学工程学报, 2015, 29(2): 471-475. YANG J L, SHA Z L, YANG L B, et al. Measurement and correlation of glycine solubility in acetone-water mixture[J]. Journal of Chemical Engineering of Chinese Universities, 2015, 29(2): 471-475. |
| [17] |
NAM K, HA E S, KIM J S, et al. Solubility of oxcarbazepine in eight solvents within the temperature range T = (288.15~308.15) K[J]. The Journal of Chemical Thermodynamics, 2017, 104: 45-49. DOI:10.1016/j.jct.2016.09.011 |




