填充床在工业中应用广泛,如热交换器、分离器、干燥器等[1-2],根据颗粒填充方式的不同,其可以分为有序填充床和随机填充床,不同填充方式对床层内传热传质过程产生较大影响。随机填充床成本低廉且操作简单,在大型填充床中有很好的适用性[3-4]。但对于小型填充床,随机填充结构却存在空间利用率低、流动阻力大等弊端,导致适用性较差。相比而言,有序填充结构具有更小的流动阻力和更大的空间利用率,并且随着3D打印技术的日趋成熟,有序填充结构较以往更易实现[5]。
近年来,小管径/粒径比(D/dp < 10)和颗粒有序填充正逐渐成为填充床研究的热点问题。ROMKES等[6]研究了有序填充床层内的流动传热特性,发现采用有序填充方式可以有效地降低流动阻力,并对传热性能产生显著影响。FREUND等[7]研究了填充床反应器内单相反应的传递过程,结果表明,压力等物理量的局部特性与全局特性均与填充床层的结构密切相关。GUNJAL等[8]研究了4种不同有序填充方式(立方堆积、1-D斜方六面体、3-D斜方六面体和面心立方)时,床层单元结构模型内的流动与传热性能。CALIS等[9]通过建立有序填充床模型,对不同小管径/粒径比床层内部流动及传热情况进行了分析,计算值与实验值吻合较好。此外,ERGUN[10]及WAKAO等[11]分别提出了适用于大管径/粒径比随机填充床层的压降和努塞尔数准则关联式,即Ergun方程和Wakao方程。在此之后,NAKAYAMA等[12]研究了不同流动方向的流体流过立方堆积填充床层的流动情况,发现所拟合阻力准则关联式的形式与Ergun方程相似,但惯性系数更小。GUARDO等[13]创建了有序填充床模型并进行了数值模拟,结果表明,获得的压降与努塞尔数计算值与Ergun方程和Wakao方程吻合较好。MIROLIAEI等[14]、ELISABETH等[15]、YANG等[16-17]也提出了类似的传热与阻力准则关联式,但是不同研究结果之间存在较大差异。
颗粒堆积结构参数的不同是导致填充床性能差异的主要原因,而其传热与阻力特性的准确预测则对填充床的合理设计与良好运行具有重要意义。本文采用数值模拟的方法,探讨了小管径/粒径比有序填充床层结构参数对流动传热性能的影响,总结了适用于小管径/粒径比有序填充床的传热与阻力性能准则关联式,并进一步从场协同的角度阐述有序填充床内部速度场与温度梯度场、速度场与压力梯度场之间的耦合协同关系。
2 物理模型和数值方法 2.1 物理模型采用体心立方堆积(body center cubic,BCC)作为颗粒排列结构单元,如图 1所示。在1个结构单元中,8个颗粒分别位于立方体的8个顶角,1个颗粒位于立方体的中心,顶角的8个颗粒均与中心的1个颗粒相切。为了减少入口、出口效应的影响,在入口及出口处均预留一部分非填充区域,长度分别为L1和L3,颗粒填充区域长度为L2。设置对称边界条件,并保留非完整颗粒形态,从而更好地反映不同填充床结构参数对于流动传热性能的影响规律。选择3组不同管径/粒径比N = D/dp进行对比分析,填充床几何参数如表 1所示。
|
图 1 计算区域物理模型 Fig.1 Physical model of computational domain |
|
|
表 1 填充床几何参数 Table 1 Geometric parameters of packed beds |
本文数值计算基于以下假设:流动为稳态、不可压缩、层流流动;忽略黏性耗散及颗粒与壁面之间的导热;颗粒表面为恒壁温边界,填充床壁面为绝热边界,无内热源。有关物理量通用控制方程为:
| ${\rm{div}}\left( {\rho U\varphi } \right) = {\rm{div}}\left( {{\mathit{\Gamma }_\varphi }{\rm{grad}}\varphi } \right) + {S_\varphi }$ | (1) |
其中,通用变量φ、广义扩散系数Γφ、广义源项Sφ取不同值时式(1)可表示为连续性方程、动量方程、能量方程[18]。
对于简单的直管内流动,当Re < 1 000时可以选择层流模型。但是对于填充床内部通道等复杂结构,层流模型的适用范围将会显著不同。JOLLS等[19]发现,填充床内流体出现湍流形态时,Re变化范围为60~130。TOBIS等[20]研究认为,填充床内流动由层流开始向湍流的转变发生在Re = 100时。因此,本文在数值计算中Re的范围选择5~30。
2.3 边界条件与数值计算方法数值计算中以水为流动工质。设置入口速度vin,根据Re不同取一系列不同值,入口温度恒定Tin = 293.15 K。采用平均静压出口边界条件,设置出口相对压力p = 0。填充床壁面与颗粒表面均设为无滑移、不可渗透、固体壁面,其中,填充床壁面采用绝热边界条件,颗粒表面设置为恒壁温Tw = 323.15 K。采用标准壁面函数法处理近壁面区域,中心纵向截面采用对称边界条件。当计算域内所有控制体积的各方程平均绝对残差小于10-5,且进出口流体质量守恒、填充床系统能量守恒时,认为迭代计算收敛。
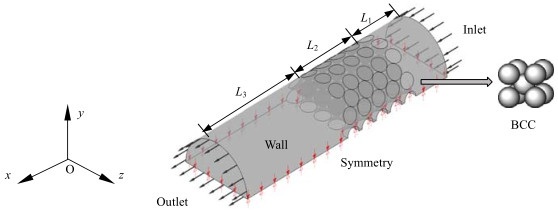
2.4 网格划分与无关性验证采用正四面体与金字塔形的非结构化网格划分,对近壁面处使用自适应网格技术(adaptive mesh refinement,AMR)以形成精细网格,设定压力、温度、速度3个物理量作为自适应变量,计算时根据自适应变量梯度大小进行3次网格细化和粗化迭代。采用间隙模型[21]解决点接触处网格质量较低的问题,将填充颗粒缩小至实际颗粒直径99%。研究表明[22],直径缩小1%以后,颗粒之间产生的空隙为滞止的狭小区域,不会对空隙的局部流动与传热造成明显影响(< 0.5%)。网格划分示意图如图 2所示。
|
图 2 网格划分示意图 Fig.2 Mesh design of the computational domain |
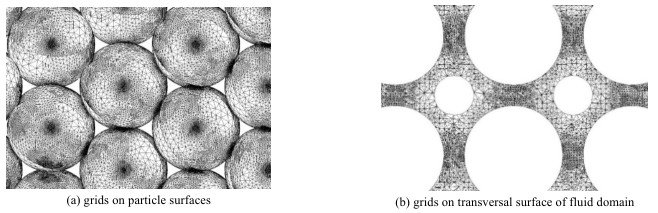
当Re = 30时,对管径/粒径比N = 5填充床计算结果进行网格无关性测试,计算得到的填充床充分发展段的压力梯度Δp/Δx和换热量Q如图 3所示。可以发现,当网格单元数大于1.67×107时,计算所得Δp/Δx和Q相差均在2%以内,满足网格无关性要求,此时的解为网格无关解,综合考虑计算效率和精度,选择此套网格进行计算。同样,可以获得其他不同N值时的填充床模型网格单元数,如表 2所示。
|
图 3 压力梯度与换热量随网格单元数的变化 Fig.3 Profiles of pressure gradient and heat exchange quantity as a function of mesh numbers |
|
|
表 2 网格参数 Table 2 Grid system parameters |
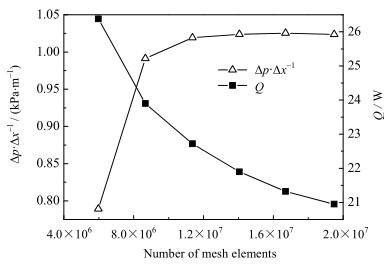
基于ROMKES等[6]和CALIS等[9]的实验结果,对本文数值方法与结果进行可靠性与准确性验证。建立管径/粒径比N = 1的计算模型,如图 4所示。其中,8个球形颗粒依次顺序填充在方形通道内,通道内流动介质为空气,入口速度为5 ≤ Re ≤ 30,入口温度Tin = 300 K,通道壁面为绝热边界条件,颗粒表面为恒壁温边界条件Tw= 310 K。采用本文数值计算方法,对上述计算模型中的流动与传热情况进行数值模拟。结果表明,阻力系数f模拟值与实验值偏差为5%~17%,Nu模拟值与实验值偏差为6%~16%,均在合理范围之内,证明了本文数值计算方法的可靠性。除了不可避免的误差外,以下原因可能造成了数值计算结果与实验数据之间的偏差:数值模拟所建模型对颗粒接触区域进行了一定的简化;通道壁面采用绝热边界条件,且忽略了相邻颗粒之间的导热,与真实情况不同等。
|
图 4 计算模型 Fig.4 Schematic diagram of the calculation model |
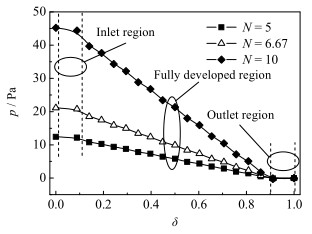
颗粒填充段通道内压力p沿填充段轴向位置δ =(x-L1)/L2的分布如图 5所示,可以看出,由于受到压差阻力与摩擦阻力的共同作用,压力p沿通道轴向呈降低的趋势。当N = 5时,填充段通道进出口的压差最小;随着N的增大,进出口压差逐渐升高。不同管径/粒径比N时,压力p沿轴向具有相似的变化规律,即:在颗粒填充段通道的流动入口段,压力p沿轴向降低的程度较弱;而随着轴向相对位置δ的增大,在流动的充分发展段,压力p沿通道轴向急剧降低,呈线性变化趋势,且N越大,压力p降低的幅度越大;在流动的出口段,压力p变化的趋势趋于平缓。
|
图 5 压力沿颗粒填充通道轴向的分布 Fig.5 Pressure distribution along the axial direction in packed channel (Re=20) |
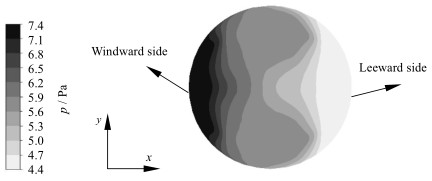
当Re = 20时,管径/粒径比N = 5填充床通道的中心颗粒表面压力分布如图 6所示。可以看出,颗粒表面迎流区域压力最高,这是由于流体的直接冲击使速度降低,动能转化为势能而使压力升高。在相邻颗粒的接触区域,流通截面积逐渐减小使得速度不断增大,压力逐渐降低,在间隙最小处流速达到局部最大值而使压力降低为局部最小值。
|
图 6 中心颗粒表面压力分布 Fig.6 Pressure distribution on the central particle surface |
在颗粒填充通道内,由于受到颗粒堆积的影响,不同位置处的局部孔隙率不同,造成流体的局部流速不同,流动分布十分复杂。由于流通截面积的变化,流体在颗粒孔隙内平均流速显然与填充床层表观速度是不同的,采用表观速度作为特征速度,无法准确描述不同颗粒填充结构时流体的流动状态。
基于上述原因,本文定义孔隙速度vϕ为特征速度:
| ${v_\rm{ϕ} } = \frac{{\left| {{{\vec v}_{\rm{D}}}} \right|}}{\phi }$ | (2) |
通过对填充通道充分发展段计算结果进行积分平均,获得流动与传热充分发展段流体的平均速度vavg如下:
| ${{v}_{\text{avg}}}=\frac{1}{V}\iiint_{V}{v}\text{d}V$ | (3) |
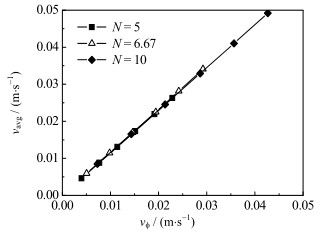
孔隙速度vϕ与颗粒孔隙内平均速度vavg的关系如图 7所示。可以看出,采用vϕ预测流体速度时,其预测值与实际平均速度vavg的偏差在15%以内,并且在不同管径/粒径比N时,相同孔隙速度vϕ下颗粒孔隙内的平均速度vavg几乎相等。以上结果表明,采用本文定义的孔隙速度作为特征速度,可以较好地反映不同颗粒填充结构时填充床层内流体的流动状态。
|
图 7 孔隙速度与平均速度的关系 Fig.7 Profile of pore velocity as a function of average velocity |
特征雷诺数Re是反映填充床内部流体流动状态的重要参数,准确定义Re是拟合传热与阻力性能关联式及研究填充床对流传热规律的首要条件,准确定义的Re应能满足在不同的床层结构下,Re相同时流体具有相似的流动状态。本文采用基于以孔隙速度v为特征速度和以孔隙尺寸dh为特征尺寸的孔隙雷诺数为特征雷诺数,定义如下:
| $Re=\frac{{{\rho }_{\text{f}}}{{v}_{\phi }}{{d}_{\text{h}}}}{{{\mu }_{\text{f}}}}$ | (4) |
| ${{d}_{\text{h}}}=\frac{4\phi }{6\left( 1-\phi \right)+{4}/{N}\;}{{d}_{\text{p}}}$ | (5) |
| ${{d}_{\text{p}}}=2{{\left( \frac{3{{V}_{\text{p}}}}{4\text{ }\!\!\pi\!\!\text{ }} \right)}^{1/3\ }}$ | (6) |
表征填充床内部阻力性能的关联式通常如下表示[10]:
| $f = \frac{{{c_1}}}{{Re}} + {c_2}$ | (7) |
| $\frac{\Delta p}{\Delta x}=f\frac{1}{2}{{\rho }_{\text{f}}}{{\left( \frac{\left| {{{\vec{v}}}_{\text{D}}} \right|}{\phi } \right)}^{2}}\frac{1}{{{d}_{\text{h}}}}$ | (8) |
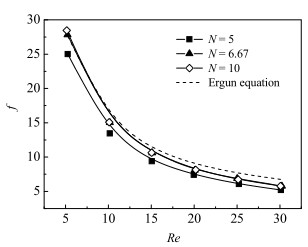
不同管径/粒径比N时,颗粒填充充分发展段阻力系数f随Re的变化如图 8所示。可以看出,阻力系数f随Re的增大先急剧减小,后逐渐趋于平缓。相同Re时,f随管径/粒径比N的增大而增大,这是由于颗粒越密集,流动分离与回流越多,造成压力损失越大。此外,当N较大(N > 6.67)时,由数值计算得到的f趋势线与由Ergun方程计算得到的f趋势线具有较高的重合度,但是随Re的增大(Re > 10),二者的偏差逐渐增大。这是因为当Re较小(Re < 10)时,黏性力占主导地位,随着Re的增大(Re > 10),边界层厚度增加,惯性力的影响逐渐增强,此时若由Ergun方程预测颗粒有序填充时的阻力系数,将会得到比数值计算值更高的f。以上结果表明,有序填充床与随机填充床内部的流体动力学特性不同,相同填充参数时,有序填充结构内流动曲迁度低于随机填充结构,因而流体扰动程度更低,流动压降更小。
|
图 8 不同管径/粒径比N时阻力系数的变化 Fig.8 Profiles of friction factor under different tube-to-particle diameter ratios |
应用最小二乘法原理,采用非线性回归分析对本文数值计算结果进行拟合,得到形如式(7)的阻力系数关联式,相关系数R2均在0.999以上,满足精度要求,式中各项系数如表 3所示。
|
|
表 3 阻力系数关联式系数 Table 3 Parameters for friction factor correlation |
综合管径/粒径比N为5、6.67、10时的数值计算结果,可得到体心立方填充时阻力系数关联式(5 ≤ Re ≤ 30)如下:
| $f=\frac{135.18}{Re}+1.17,\text{ }\ {{\text{R}}^{2}}=0.990$ | (9) |
将式(9)与Ergun方程(c1 = 133,c2 = 2.33)对比发现,两式中代表黏性效应的c1值差异不大,而代表惯性效应的c2值在式(9)中比在Ergun方程中小49.8%。可见,用Ergun方程预测小管径/粒径比有序填充床的阻力性能时将会带来一定的偏差,Ergun方程的预测值更高。
3.4 管径/粒径比对传热性能的影响表征填充床内部传热性能的关联式如下[11]:
| $Nu=\frac{h\cdot {{d}_{\text{p}}}}{{{\lambda }_{\text{f}}}}={{a}_{1}}+{{a}_{2}}P{{r}^{{1}/{3}\;}}R{{e}^{\text{n}}}\cdot {{\left( \frac{{{d}_{\text{p}}}}{{{d}_{\text{h}}}}\phi \right)}^{\text{n}}}$ | (10) |
不同管径/粒径比N时,颗粒填充充分发展段努塞尔数Nu随Re的变化如图 9所示。可以看出,当Re相同时,随着管径/粒径比N的增大,即随着同层颗粒数的增加,努塞尔数增大。这是因为随着颗粒数量的增多,颗粒对流体的扰动越来越强烈,加剧了流体的混合,从而提高了传热速率。由Wakao方程计算得到的Nu明显高于本文数值计算得到的Nu,而且二者的差距随着Re的增大而愈加显著。
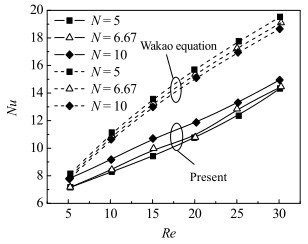
|
图 9 不同管径/粒径比N时努塞尔数的变化 Fig.9 Profiles of Nusselt number under different tube-to-particle diameter ratios |
将本文结果拟合得到形如式(10)的努塞尔数关联式,式中各项系数如表 4所示,关联式相关系数R2均在0.989以上,满足精度要求。综合管径/粒径比N为5、6.67、10时的数值计算结果,可得到体心立方填充时努塞尔数关联式(5 ≤ Re ≤ 30)如下:
|
|
表 4 努塞尔数关联式系数 Table 4 Parameters for Nusselt number correlation |
| $Nu=6.43+0.068P{{r}^{{1}/{3}\;}}R{{e}^{1.18}}\cdot {{\left( \frac{{{d}_{\text{p}}}}{{{d}_{\text{h}}}}\phi \right)}^{1.18}} , {{\text{R}}^{2}}=0.934$ | (11) |
将式(11)与Wakao方程(a1 = 2.0,a2 = 1.1,n = 0.6)进行比较,两式a1值和n值相差不大,但Wakao方程中a2值比式(11)中a2值大15倍。
3.5 颗粒填充通道对流传热的场协同分析GUO等[23]提出了传热优化的场协同理论,指出当速度场与温度梯度场绝对值一定时,为了强化传热,应该使速度矢量与温度梯度矢量之间的夹角α尽可能小(α < 90°)或α尽可能大(α > 90°)。何雅玲等[24]、刘伟等[25]在场协同理论的基础上,分析了速度场与压力梯度场之间的协同性,认为其夹角θ越大,速度场与压力梯度场的协同性越好,压力梯度的作功能力越强,产生的压降越小。
对流传热区域速度场与温度梯度场的整体场协同性可采用平均协同角αm衡量,定义如下:
| ${\alpha _{\rm{m}}} = \arccos \left( {\sum {\cos } {\alpha _i}\frac{{\left| {{\mathit{\boldsymbol{v}}_i}} \right|\left| {\nabla {T_i}} \right|{\rm{d}}{V_i}}}{{\sum {\left| {{\mathit{\boldsymbol{v}}_i}} \right|} \left| {\nabla {T_i}} \right|{\rm{d}}{V_i}}}} \right)$ | (12) |
| ${\alpha _i} = \arccos \left( {\frac{{{\mathit{\boldsymbol{v}}_i} \cdot \nabla {T_i}}}{{\left| {{\mathit{\boldsymbol{v}}_i}} \right|\left| {\nabla {T_i}} \right|}}} \right)$ | (13) |
本文计算αm时引入流速与温度梯度乘积的权重,与已有文献中的计算方法[26-27]相比,突出了高流速与高温度梯度区域协同角的贡献,同时将协同角的平均改进为协同角余弦值的平均,更能真实体现场协同性能的均值。
颗粒填充段内速度与温度梯度的平均协同角αm随Re的变化如图 10所示。从图中可以看出,随着Re的增大,不同管径/粒径比N时αm均增大,表明速度场与温度梯度场的协同性随着Re的增大而变差,因此传热的增强主要是由于流速的增大引起的。当Re相同时,平均协同角αm随管径/粒径比N的增大而减小,速度场与温度梯度场的协同性更好,传热情况更好。
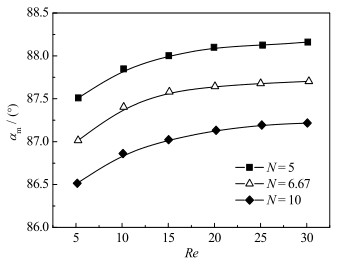
|
图 10 速度与温度梯度平均协同角的变化 Fig.10 Profiles of the average synergy angle with temperature gradient as a function of velocity |
为了对整个流场的速度场与压力梯度场之间的协同性作出定量评价,参照式(12),定义全局平均协同角θm为:
| ${\theta _{\rm{m}}} = \arccos \left( {\sum {\cos } {\theta _i}\frac{{\left| {{\mathit{\boldsymbol{v}}_i}} \right|\left| {\nabla {p_i}} \right|{\rm{d}}{V_i}}}{{\sum {\left| {{\mathit{\boldsymbol{v}}_i}} \right|} \left| {\nabla {p_i}} \right|{\rm{d}}{V_i}}}} \right)$ | (14) |
| ${\theta _i} = \arccos \left( {\frac{{{\mathit{\boldsymbol{v}}_i} \cdot \nabla {p_i}}}{{\left| {{\mathit{\boldsymbol{v}}_i}} \right|\left| {\nabla {p_i}} \right|}}} \right)$ | (15) |
图 11为速度场与压力梯度场的全局平均协同角θm随Re的变化。随着Re的增大,不同管径/粒径比N时θm均增大,表明速度场与压力梯度场的协同性随着Re的增大而变好,可见流动阻力随着Re的增大而增加主要是由于流速的增大引起的。当Re相同时,全局平均协同角θm随管径/粒径比N的减小而增大,表明压力梯度的做功能力更强,产生的压降更小。
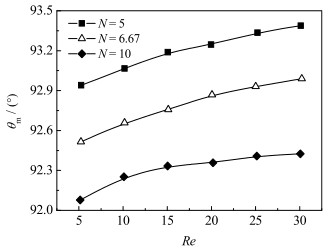
|
图 11 速度与压力梯度平均协同角的变化 Fig.11 Profiles of the average synergy angle with pressure gradient as a function of velocity |
(1) 流体压力沿颗粒填充通道轴向的变化趋势在不同阶段各不相同,不同管径/粒径比时具有相似的规律。
(2) 随着管径/粒径比的增加,颗粒填充充分发展段努塞尔数不断增大,阻力系数亦有同样的变化趋势。
(3) 对于小管径/粒径比颗粒有序填充床,Ergun方程预测阻力系数时出现偏差,且管径/粒径比越小偏差越大;不同管径/粒径比时,Wakao方程关于努塞尔数的预测值均偏高,偏差随着Re的增加而增大。
(4) 随着Re的增大,速度场与温度梯度场、速度场与压力梯度场之间的平均协同角均变大;随着管径/粒径比的增大,速度场与温度梯度场、速度场与压力梯度场之间的平均协同角均变小。
| 符号说明: | |||
| D | -圆筒直径,mm | T | -温度,K |
| dh | -孔隙水力直径,mm | V | -体积,mm3 |
| dp | -颗粒直径,mm | v | -流速,m·s-1 |
| f | -阻力系数 | vD | -达西速度,m·s-1 |
| h | -表面传热系数,W·m-2·K-1 | x, y, z | -三维坐标,mm |
| L1 | -入口段长度,mm | α | -速度与温度梯度的协同角,° |
| L2 | -填充段长度,mm | θ | -速度与压力梯度的协同角,° |
| L3 | -出口段长度,mm | λ | -导热系数,W·m-1·K-1 |
| N | -管径/粒径比,即圆筒直径与颗粒直径之比 | ρ | -密度,kg·m-3 |
| Nu | -努塞尔数 | ϕ | -孔隙率 |
| Pr | -普朗特数 | 下标 | |
| p | -压力,Pa | f | -流体 |
| Q | -换热量,W | in | -入口 |
| Re | -雷诺数 | p | -颗粒 |
| R2 | -相关系数 | w | -壁面 |
| [1] |
KERTALLI E, KOSINOV N, SCHOUTEN J C, et al. Direct synthesis of propylene oxide in a packed bed membrane reactor[J]. Chemical Engineering Journal, 2017(307): 9-14. |
| [2] |
SINGH P L, DESHPANDEY S D, JENA P C. Thermal performance of packed bed heat storage system for solar air heaters[J]. Energy for Sustainable Development, 2015(29): 112-117. |
| [3] |
LIU Y, WANG J Y, CHENG Z L, et al. Experimental investigation of fluid flow and heat transfer in a randomly packed bed of sinter particles[J]. International Journal of Heat and Mass Transfer, 2016(99): 589-598. |
| [4] |
JIANG L S, LIU H S, SUO S Y, et al. Pore-scale simulation of flow and turbulence characteristics in three-dimensional randomly packed beds[J]. Powder Technology, 2018(338): 197-210. |
| [5] |
李龙, 闫孝红, 杨剑, 等. 三维颗粒有序堆积床内传质数值研究[J]. 工程热物理学报, 2015, 36(4): 870-873. LI L, YAN X H, YANG J, et al. Three-dimensional numerical study on mass transfer in ordered packed beds[J]. Journal of Engineering Thermophysics, 2015, 36(4): 870-873. |
| [6] |
ROMKES S J P, DAUTZENBERG F M, VAN DEN BLEEK C M, et al. CFD modelling and experimental validation of particle-to-fluid mass and heat transfer in a packed bed at very low channel to particle diameter ratio[J]. Chemical Engineering Journal, 2003, 96(1/2/3): 3-13. |
| [7] |
FREUND H, ZEISER T, HUBER F, et al. Numerical simulations of single phase reacting flows in randomly packed fixed-bed reactors and experimental validation[J]. Chemical Engineering Science, 2003, 58(3/4/5/6): 903-910. |
| [8] |
GUNJAL P R, RANADE V V, CHAUDHARI R V, et al. Computational study of a single-phase flow in packed beds of spheres[J]. AIChE Journal, 2005, 51(2): 365-378. DOI:10.1002/aic.10314 |
| [9] |
CALIS H P A, NIJENHUIS J, PAIKERT B C, et al. CFD modelling and experimental validation of pressure drop and flow profile in a novel structured catalytic reactor packing[J]. Chemical Engineering Science, 2001, 56(4): 1713-1720. DOI:10.1016/S0009-2509(00)00400-0 |
| [10] |
ERGUN S. Fluid flow through packed columns[J]. Chemical Engineering and Processing, 1952, 48(2): 89-94. |
| [11] |
WAKAO N, KAGUEI S. Heat and mass transfer in packed beds[M]. New York: McGraw-Hill, 1982.
|
| [12] |
NAKAYAMA A, KUWAHARA F, KAWAMURA T, et al. Three-dimensional numerical simulation of flow through a microscopic porous structure[C]//ASME/JSME Thermal Engineering Conference, 1995: 313-318.
|
| [13] |
GUARDO A, COUSSIRAT M, LARRAYOZ M A, et al. Influence of the turbulence model in CFD modeling of wall-to-fluid heat transfer in packed beds[J]. Chemical Engineering Science, 2005, 60(6): 1733-1742. DOI:10.1016/j.ces.2004.10.034 |
| [14] |
MIROLIAEI A R, SHAHRAKI F, ATASHI H. Computational fluid dynamics simulations of pressure drop and heat transfer in fixed bed reactor with spherical particles[J]. Korean Journal Chemical Engineering, 2011, 28(6): 1474-1479. DOI:10.1007/s11814-010-0507-x |
| [15] |
ELISABETH S, ANDREAS C, LAMBERT K. Measurements of heat transfer between particles and gas in packed beds at low to medium Reynolds numbers[J]. Experimental Thermal and Fluid Science, 2006, 30(6): 545-558. DOI:10.1016/j.expthermflusci.2005.11.002 |
| [16] |
YANG J, WANG Q W, ZENG M, et al. Computational study of forced convective heat transfer in structured packed beds with spherical or ellipsoidal particles[J]. Chemical Engineering Science, 2010, 65(2): 726-738. |
| [17] |
YANG J, WANG J, BU S S, et al. Experimental analysis of forced convective heat transfer in novel structured packed beds of particles[J]. Chemical Engineering Science, 2012(71): 126-137. |
| [18] |
陶文铨. 数值传热学[M]. 西安: 西安交通大学出版社, 2001. TAO W Q. Numerical heat transfer[M]. Xi'an: Xi'an Jiaotong University Press, 2001. |
| [19] |
JOLLS K R, HANRATTY T J. Transition to turbulence for flow through a dumped bed of spheres[J]. Chemical Engineering Science, 1966, 21(12): 1185-1190. DOI:10.1016/0009-2509(66)85038-8 |
| [20] |
TOBIS J, ZIóLKOWSKI D. Modeling of heat transfer at the wall of a packed-bed apparatus[J]. Chemical Engineering Science, 1988, 43(11): 3031-3036. DOI:10.1016/0009-2509(88)80056-3 |
| [21] |
LEE J J, PARK G C, KIM K Y, et al. Numerical treatment of pebble contact in the flow and heat transfer analysis of a pebble bed reactor core[J]. Nuclear Engineering and Design, 2007, 237(22): 2183-2196. DOI:10.1016/j.nucengdes.2007.03.046 |
| [22] |
NIJEMEISLAND M, DIXON A G. Comparison of CFD simulations to experiment for convective heat transfer in a gas-solid fixed bed[J]. Chemical Engineering Journal, 2001, 82(1/2/3): 231-246. |
| [23] |
GUO Z Y, LI D Y, WANG B X. A novel concept for convective heat transfer enhancement[J]. International Journal of Heat and Mass Transfer, 1998, 41(14): 2221-2225. DOI:10.1016/S0017-9310(97)00272-X |
| [24] |
何雅玲, 雷勇刚, 田丽亭, 等. 高效低阻强化换热技术的三场协同性探讨[J]. 工程热物理学报, 2009, 30(11): 1904-1906. HE Y L, LEI Y G, TIAN L T, et al. An analysis of three-field synergy on heat transfer augmentation with low penalty of pressure drop[J]. Journal of Engineering Thermophysics, 2009, 30(11): 1904-1906. DOI:10.3321/j.issn:0253-231X.2009.11.028 |
| [25] |
刘伟, 刘志春, 马雷. 多场协同原理在管内对流强化传热性能评价中的应用[J]. 科学通报, 2012, 57(10): 867-874. LIU W, LIU Z C, MA L. Physical quantity application of a multi-field synergy principle in the performance evaluation of convective heat transfer enhancement in a tube[J]. Chinese Science Bulletin, 2012, 57(10): 867-874. |
| [26] |
郭江峰.换热器的热力学分析与优化设计[D].济南: 山东大学, 2011. GUO J F. Thermodynamic analysis and optimization design of heat exchanger[D]. Jinan: Shandong University, 2011. |
| [27] |
何雅玲, 陶文铨. 强化单相对流换热的基本机制[J]. 机械工程学报, 2009, 45(3): 27-38. HE Y L, TAO W Q. Fundamental mechanism of enhancing single-phase convective heat transfer[J]. Journal of Mechanical Engineering, 2009, 45(3): 27-38. |




