2. 杭州奥盛仪器有限公司, 浙江 杭州 310012
2. Hangzhou Allsheng Instrument Co. Ltd., Hangzhou 310012, China
毛细管电泳(CE)是一种典型的液相分离技术,其通常以弹性石英毛细管为分离通道,以高压直流电场为驱动力,根据样品中不同组分间电泳迁移速率和分配行为的差异,实现高效快速分离。然而在高压电场作用下,电解质在通道中会产生焦耳热,导致谱带展宽,从而影响分离效果[1]。为了降低焦耳热对分离效果的影响,通常采用外制冷的方式对毛细管进行冷却,其中液冷和气冷是目前大多数电泳仪器采用的主流冷却方式。液体比热容较大,散热效率优于气冷,而气体冷却则更加安全、成本低廉,并且不存在漏液、换液的问题[2]。实验表明,当空气流速达到一定速率(大于10 m⋅s−1)后,空气冷却与液体冷却的效果相当[3-5]。
风道是冷却系统的重要组成部分,合理的风道设计能很大程度提升冷却效率。但是目前部分产品中由于结构设计原因,分离段毛细管冷却不够均匀,从而导致轴向温差较大,最终影响分离结果。本研究在毛细管柱冷却风道的结构设计中利用计算流体力学(CFD)进行仿真分析,对已有的结构进行建模求解,分析原因,选择合理的进风角度,并根据CFD分析结果不断优化出入口面形状、长宽比以及风道尺寸等参数,提升了柱表面的风速均匀性与冷却后柱面的温度均匀性,大幅缩短了试验周期[6]。最终通过试验验证了仿真优化的合理性,同时分离段的平均温差满足设计要求的标准,有效降低了焦耳热对分离的影响。
2 典型毛细管冷却风道仿真分析 2.1 几何模型简化首先,将典型的毛细管冷却风道结构进行简化,随后利用Solidworks软件进行三维建模,见图 1(a),如图所示20 ℃的空气以11 m⋅s−1的速度从入口进入,在转向的同时对毛细管柱进行冷却。将模型导入SpaceClaim中对各个面命名。采用高韧树脂作为风道壁面材料,考虑到毛细管在高压环境下会产生焦耳热,本研究用直径为0.36 mm、长度为270 mm且发热功率为1 W的不锈钢柱模拟毛细管发热,漏风与接触间的传热可忽略。当圆柱的长度远大于其直径且风道宽度大于20倍圆柱直径时,风道边界层不会影响圆柱附近的流动,即可忽略风道的壁面效应[7]。
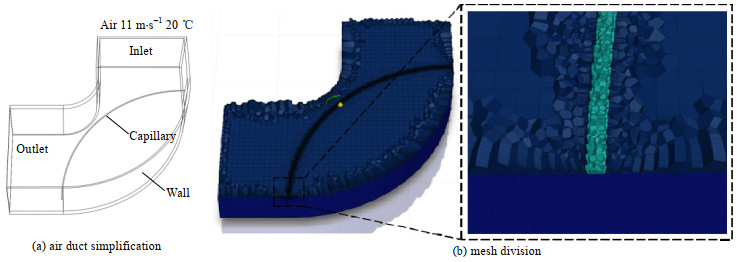
|
图 1 典型风道简化模型与网格划分 Fig.1 Simplified model and mesh division of a typical air duct |
采用Fluent Meshing建立网格。由于空气冷却时壁面速度、压力梯度大,需要对圆柱表面局部网格尺寸加密,同时添加边界层设置,最后用Poly-Hexcore绘制六面体网格,提高仿真精度[8-9]。具体网格划分如图 1(b)所示。为了研究网格数量对计算结果的影响,采用逐步加密的方法,建立了5种不同网格数的模型,并对计算结果进行分析[10]。表 1总结了不同网格尺寸下对柱面最低温的影响,以及相对应的误差。由表 1可知,随着网格数的增加,最低温变化不大,当网格数量为143 242时,误差最小为0.279 %。因此确定最佳网格数量为143 242,其中最大纵横比为34.37,在达到计算精度的前提下保证计算资源利用最大化[11]。
|
|
表 1 网格尺寸对柱面最低温的影响 Table 1 Effects of grid size on minimum temperature at the column surface |
Janjua等[12]在对水平放置的圆柱进行横流热性能数值研究时,与实测数据比较后发现,在低雷诺数下(< 2 000),采用层流模型和RSM-BSL模型均能准确预测结果,但当雷诺数增加后,RSM-BSL模型的预测结果更加精准。Szczepanik等[13]在研究横流中圆柱的传热性能时,采用SST k-ω湍流模型进行计算,经验证该模型对边界层和涡流区域的流动和传热有较强的预测能力。结合本研究内容,低雷诺数下的圆柱横流仍会出现扰动和不均匀性,为获得更加可靠和准确的计算结果,研究采用SST k-ω湍流模型。
在计算模型中,将不锈钢柱源项功率设定为3.27×107 W⋅m3;进风口定为速度入口,空气的送风速度为11 m⋅s−1,送风温度为20 ℃,出风口定为压力出口。不考虑柱壁面与风道面的滑移条件和柱两端面的传热,只考虑风道内的柱面对流传热。
数值模拟涉及压差和要求高精度收敛,因此采用双精度求解器进行求解。采用Coupled格式求解压力-速度耦合问题,该方法可以将连续方程、能量方程、动量方程同时求解,适合稳态单相流数值计算,对有效性和鲁棒性均有大幅提升[9]。将能量的收敛条件设置为1.0×10−9,其余物理量收敛条件皆为1.0×10−5。将压力出口的质量流率和柱面平均温度设置为监测项,观察其收敛性。标准初始化后进行求解计算。
2.4 仿真结果分析仿真结果分析如图 2所示,图中t为柱面温度,℃;va为空气流速,m⋅s−1。由图 2(a)可知,空气掠过后柱面温度下降,中间温度高,两端温度低,最低温为24.23 ℃,最高温为29.81 ℃,柱面温差为5.58 ℃,温度均匀性和冷却效果较差。由图 2(b)可知,空气流速在内径拐弯处骤升,但换热效率低,柱面温度较高。风道内空气流速分布的不均匀直接产生了较大的柱面温差。通过观察图 2(c)可知,空气流动的速度方向与柱面切线方向的夹角呈现出两端大中间小的变化趋势,因此中间的圆柱面虽然流经的空气流速大,但传热效果却不及两端。由图 2(d)可知,出口处的运动迹线紊乱,形成了涡流与回流,不仅造成了风量损失,而且不利于整段柱壁面的均匀散热。
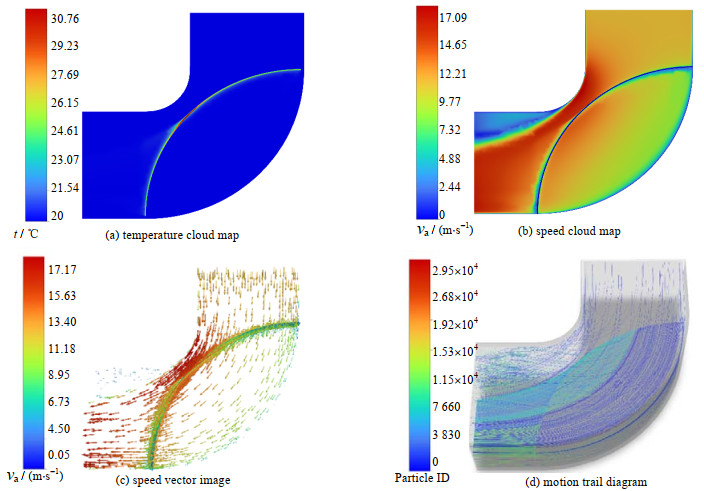
|
图 2 典型风道仿真分析 Fig.2 Simulation analysis of a typical air duct |
流体的速度方向与柱壁面切线方向的夹角被称为冲击角,冲击角修正系数εϕ随着冲击角ϕ的增大而增大,但不超过1[14]。
努塞尔数Nu与冲击角修正系数εϕ关联式如式(1)所示[14]。
| $ Nu = CR{e^m}Pr_{\text{f}}^{0.36}{\left( {\frac{{P{r_{\text{f}}}}}{{P{r_{\text{w}}}}}} \right)^{0.25}}{\varepsilon _n}{\varepsilon _\phi } $ | (1) |
式中:Nu为努塞尔数;C和m为对应雷诺数Re范围下的常数;Prf为以流体进出口的平均温度为定性温度的普朗特数;Prw为以圆柱壁面温度作为定性温度的普朗特数;εn为管排修正系数,本研究可忽略不计。
Re可由式(2)求解:
| $ Re = \frac{{\rho vl}}{\mu } $ | (2) |
式中:ρ为流体密度,kg⋅m−3;v为流体流速,m⋅s−1;l为特征长度,常以管径作为参考,m;μ为流体的动力黏度,Pa⋅s。
普朗特数Pr可由式(3)求解:
| $ Pr = \frac{{C\mu }}{\lambda } $ | (3) |
式中:C为流体的比热容,J⋅kg−1⋅K−1;λ为流体热导率,W⋅m−1⋅K−1。
因此,在特定情况下Nu与εϕ成正比,当冲击角达到90°时,冲击角εϕ达到最大值,Nu也最大。对流换热系数h与努塞尔数Nu关联式如式(4)所示:
| $ h = \frac{\lambda }{l}Nu $ | (4) |
式中:h为对流换热系数,W⋅m−2⋅K−1。
在特定情况下努塞尔数Nu与对流换热系数h也成正比,因此当冲击角为90°时,对流传热效率达到峰值。
3.2 卡盒模型优化为了优化空气掠过管柱的冲击角,实现散热效率最大化,本研究自主设计了一款新型毛细管卡盒,如图 3所示。其中AB段为进样部分,BC段为分离部分,CD段为检测部分,DE段为出样部分[15]。由于BC段是直接影响分离和检测结果的关键,因此本次设计着重考虑该段冷却。该卡盒风道与典型卡盒风道区别在于:空气从Z方向横掠分离段管柱,保证了分离段整段管柱冲击角都能最大化。
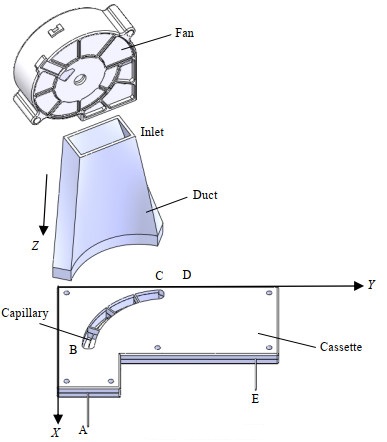
|
图 3 风道初步设计 Fig.3 Preliminary design of the air duct |
涡流风扇具有体积小、风力大、散热效果显著等特点,本研究中风扇选择为DELTA的BFB0712HH-A型号涡流风扇,出风口为35.9 mm×17.5 mm的矩形,风速也满足设计需求。外风道的初步设计如图 3所示。一定温度的空气经涡流风扇旋转加速、风道导流后均匀地吹向卡盒BC段发热的毛细管,从而达到降温目的,提高分离效率。
设计外风道是为了将风扇出风口的高速空气均匀、高效地导流到发热的柱表面,达到均匀散热的要求。但是入风口和出风口如果连接不够顺滑,则会导致一定的风量损失,因此风道的出入口采用流线型设计,尽量避免截面积发生突变。为了简化模型,在确保反映真实流动特征的前提下,忽略流动、传热之外的因素[16-17]。
为了探究入风口矩形长宽比对散热效果的影响,在面积不变的情况下设计了3组长宽比分别为1:1、1:2、1:3的外风道模型。由于几何结构的优化,重新对该模型进行网格独立性验证,最终确定网格数为213 223。经仿真计算得到的柱面最低温tmin、最高温tmax、柱面温差Δt如表 2所示。由表 2可得,入风口矩形的长宽比对最终的柱面温差影响较小,为了与涡流风扇更高效地转接,减少中途因截面变化引起的压力、风量损失,长宽比最终选定为1:2 (35.9 mm×17.5 mm)。
|
|
表 2 入风口长宽比对柱温的影响 Table 2 Effects of inlet aspect ratio on column temperature |
为了与卡盒风道对应连接,进一步对比了出风口两端圆角与倒角设计对温差的影响,分别设置了圆角R=3、倒角C=3两次仿真,结果显示对出风口增设圆角后温差变为0.63 ℃,增设倒角后温差变为0.68 ℃。因此,出风口的倒圆角设置对温差影响很小。
3.3.2 风道长度尺寸优化风道长度尺寸优化如图 4所示,卡盒厚度固定,因此卡盒内风道长度为9 mm不变,为了确定外风道的最佳长度l1,在不同外风道长度下分别对其进行仿真计算,并对收敛后的柱面温度极值进行数值分析。如表 3所示,l1从25 mm增加到250 mm,风道内柱面的温差呈现出先减小后增加的趋势,当l1为175 mm时,柱面温差最小,温度均匀性较高。因此在实际的工程运用中,在保证高效的散热效果的前提下,选择l1=175 mm为外风道总长。
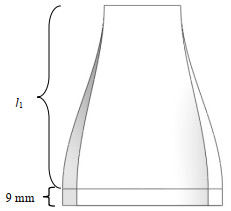
|
图 4 外风道模型长度优化示意图 Fig.4 Schematic diagram of the optimized length of external duct model |
|
|
表 3 外风道长度对柱温的影响 Table 3 Effects of outer air duct length on column temperature |
通常变截面风道会因为静压的改变导致风道内流体的细微变化,因此增加一段等截面风道使流体过渡平稳。如图 5所示,在外风道总长(175 mm)不变的前提下,进一步探究了变截面风道与等截面风道的长度比对柱面温差的影响,经仿真计算后对柱面温度极值进行数值分析。由表 4可知,l2: l3为1:1时,即两风道长度相同,柱面温差达到最小,温度均匀性最好。
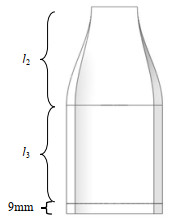
|
图 5 两风道长度比优化示意图 Fig.5 Schematic diagram of the length ratio of two air ducts after optimization |
|
|
表 4 两风道长度比对柱温的影响 Table 4 Effects of two duct length ratio on column temperature |
优化后柱面的温度分布轮廓云图如6(a)所示,柱面的温度分布呈现两端高、中间低的状态,相较于优化前的柱面温差,优化后的温度均匀性已有大幅提高。柱切面的速度分布云图如图 6(b)所示,冷却风道内柱面的空气流速分布更加均匀。
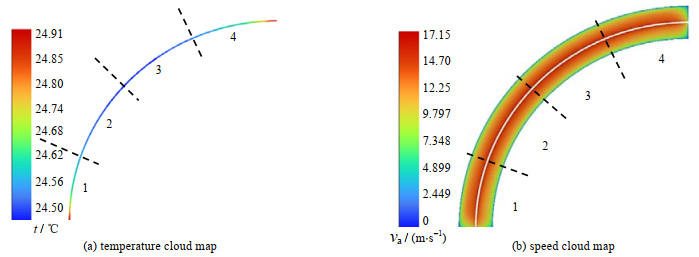
|
图 6 优化后的风道仿真温度和速度云图 Fig.6 The optimized duct simulation temperature profile and velocity clouds |
优化后的风道模型的速度矢量图如图 7(a)所示,整个冷却段的柱面所受冲击角几乎都达到90°,对流传热能力显著增强。从风道内的运动迹线图 7(b)可知,流过柱面的迹线流畅平稳,并未出现迹线紊乱、涡流等问题[18]。
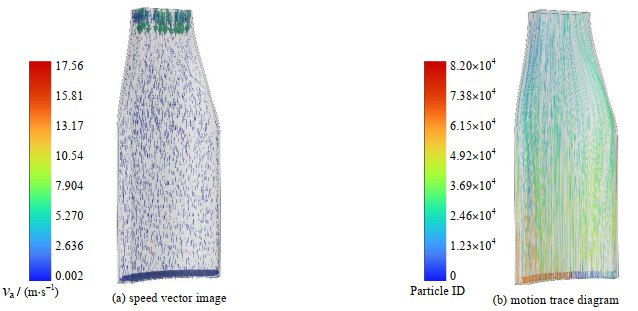
|
图 7 优化后的风道仿真速度矢量与运动迹线图 Fig.7 Simulation velocity vectors and motion trace diagram of the air duct after optimization |
为了验证仿真结果的准确性,对所设计的模型通过3 D打印得到实物,并设计两组实测实验,分别是出风口风速实测与冷却稳定后柱面温度实测。风速测量采用Testo 405 i热敏风速仪,其测量范围为0.6~30 m⋅s−1,测量精度为±(0.3 m⋅s−1+5% 测量值);温度采集使用Testo 890红外成像仪,其测量范围为−30~600 ℃,测量精度为±2 ℃或±2% 测量值[19]。
由于卡盒内的管柱在高速空气吹动下会产生跳动影响实验结果,所以加工时在卡盒内风道增加了3段固定加强筋,并将出风口分为4个区域如图 8(a)所示。将室内空气温度保持在20 ℃ ± 0.5 ℃,使用热敏风速仪分别在4个区域中心持续作用20 s,采集每秒产生的风速数值,计算得到的平均值即为风速实测值;仿真风速数据取值为速度分布云图 6(b)中对应的4个区域,在每个区域内取多个风速值得到的区域均值[20]。

|
图 8 实测验证 Fig.8 Experimental verification results |
为了得到仿真柱面温差与实测柱面温差数据对比,在温度分布轮廓云图 6(a)中的4个区域,在区域内均匀取多个温度点得到仿真温度区域均值;在Testo自带的分析软件IR-Soft红外温度云图中每个区域均匀取3个温度点得到实测温度区域均值,如图 8(b)所示。
风道出风口风速与冷却后柱面温度的仿真与实测值对比如图 9所示。
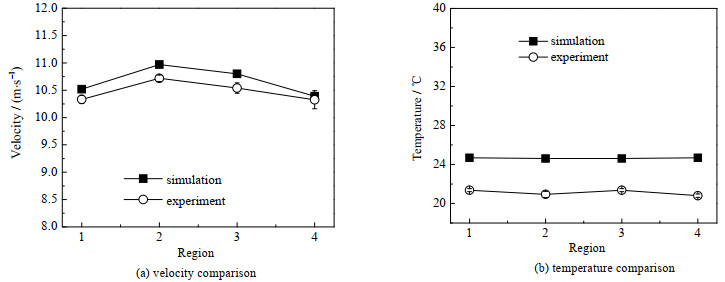
|
图 9 仿真和实测数据对比图 Fig.9 Comparison of simulation and measured data |
结果显示,实测风速数值整体略小于仿真风速数值。这主要是由于风道内壁存在摩擦和沿程阻力,以及风道与卡盒连接处存在细小漏风问题。此外3段固定加强筋也导致了风道内一定的风量损失。这些因素导致了实测风速与仿真风速之间的差异。实测温度整体小于仿真温度的主要原因是:为了简化模型,仿真计算将柱两端设置为热通量为零,没有考虑轴向的柱内热量传导。而在实际测量的过程中,风道以外的柱面散热加快,导致温度降低,从而经柱内传导后降低了风道内柱面温度,因此实测的温度值低于仿真温度值。实测的温度范围为20.8~21.6 ℃,考虑存在测量误差为±2% 实测值,最终风道内整体的柱面温差仍小于±1 ℃,表明了该均匀送风道设计的可靠性。
5 结论针对毛细管冷却风道内分离段轴向散热不均匀问题进行了研究,利用Fluent软件对风道进行仿真分析,基于分析结果优化了风道模型,并通过实测验证了设计的可靠性。最终得出以下结论:
1) 典型的毛细管冷却风道由于分离段柱面所受的冲击角差异,导致柱面温差大,冷却效果差从而影响分离效果。
2) 变截面风道中的流体需要一定长度的等截面风道过渡以确保其平稳变化。
3) 通过改变入风方向与改进冲击角,优化的毛细管冷却风道改善了柱面的风速均匀性和温度均匀性。经实测验证,证明了优化风道的可靠性。
| [1] |
曹军, 洪芳军, 郑平. 焦耳热效应对毛细管电泳中样品区带传输的影响[J]. 化学工程, 2008, 36(7): 71-73, 78. CAO J, HONG F J, ZHENG P. Influence of Joule heating effects on sample band transport in capillary zone electrophoresis[J]. Chemical Engineering (China), 2008, 36(7): 71-73, 78. |
| [2] |
何意. 空气冷却作用在燃气热水器燃烧室系统的研究与应用[J]. 日用电器, 2021(8): 66-70. HE Y. Research and application of air cooling effect on combustion chamber system of gas water heater[J]. Electrical Appliances, 2021(8): 66-70. |
| [3] |
VERAART J R, GOOIJER C, LINGEMAN H. Thermostating in capillary electrophoresis[J]. Chromatographia, 1997, 44(3): 129-134. |
| [4] |
HEIGER D N. High performance capillary electrophoresis: an introduction [M]. 2nd ed. Paris: Hewlett Packard Company, 1992.
|
| [5] |
VERAART J R, LINGEMAN H, GOOIJER C. Temperature control in capillary electrophoresis systems[J]. Biomedical Chromatography, 1995, 9(6): 271-272. DOI:10.1002/bmc.1130090612 |
| [6] |
刘智远, 朱颖谋, 毛业军, 等. 多出风口牵引风道流场仿真及结构优化设计研究[J]. 技术与市场, 2021, 28(5): 26-29. LIU Z Y, ZHU Y M, MAO Y J, et al. Simulation of flow field and structural optimization design of multi-outlet traction duct[J]. Technology and Market, 2021, 28(5): 26-29. |
| [7] |
HAIDER M J, DANISH S N, KHAN W A, et al. Heat transfer and fluid flow over circular cyclinders in cross flow[J]. NUST Journal of Engineering Sciences, 2010, 3(1): 68. |
| [8] |
BEHRAVESH M M, SAFFARIAN M R, BAHRAINIAN S S. Investigating the possibility of increasing cooling air flow in a hydrogenerator rotor fan[J]. Journal of Thermal Analysis and Calorimetry, 2021, 145(5): 2633-2646. DOI:10.1007/s10973-020-09813-6 |
| [9] |
董岭, 陈瑞, 沈渊, 等. 负压式烧结板除尘器风道仿真分析[J]. 建筑机械, 2022(10): 121-124. DONG L, CHEN R, SHEN Y, et al. Simulation analysis of air duct of negative pressure sintered plate dust collector[J]. Construction Machinery, 2022(10): 121-124. |
| [10] |
马世超, 樊明敬, 郝本华, 等. 空调室内机风道结构影响风量噪声仿真及实验研究[J]. 家电科技, 2022(3): 42-46. MA S C, FAN M J, HAO B H, et al. Simulation and experimental study on the influence of air flow noise on indoor unite air duct system[J]. Journal of Appliance Science and Technology, 2022(3): 42-46. |
| [11] |
SHEIKHOLESLAMI M, GORJI-BANDPY M, GANJI D D. Fluid flow and heat transfer in an air-to-water double-pipe heat exchanger[J]. The European Physical Journal Plus, 2015, 130(11): 225. DOI:10.1140/epjp/i2015-15225-y |
| [12] |
JANJUA M M, KHAN N U, KHAN W A, et al. Numerical study of forced convection heat transfer across a cylinder with various cross sections[J]. Journal of Thermal Analysis and Calorimetry, 2021, 143(3): 2039-2052. DOI:10.1007/s10973-020-10297-7 |
| [13] |
SZCZEPANIK K, OOI A, AYE L, et al. A numerical study of heat transfer from a cylinder in cross flow: Proceedings of the 15th Australasian Fluid Mechanics Conference [C]. Sydney: [s. n.], 2004.
|
| [14] |
刘彦丰, 梁俊秀, 高正阳, 等. 传热学[M]. 2版. 北京: 中国电力出版社, 2021. LIU Y F, LIANG J X, GAO Z Y, et al. Heat transfer [M]. 2nd ed. Beijing: China Electric Power Publishing House, 2021. |
| [15] |
MATEUSZ NOWAK P, WOŹNIAKIEWICZ M, KOŚCIELNIAK P. A simple method for assessment and minimization of errors in determination of electrophoretic or electroosmotic mobilities and velocities associated with the axial electric field distortion[J]. Electrophoresis, 2015, 36(24): 2994-3001. DOI:10.1002/elps.201500206 |
| [16] |
王良柱, 张蒙, 徐静. 基于Fluent的汽车空调风道仿真及结构改进[J]. 机械, 2021, 48(1): 30-36. WANG L Z, ZHANG M, XU J. Simulation and structural improvement of air duct of automobile rear air conditioner based on fluent[J]. Machinery, 2021, 48(1): 30-36. |
| [17] |
姜洋, 龙曦, 朱禹, 等. 风冷电池包风道设计与仿真优化分析[J]. 汽车工程师, 2020(5): 27-30. JIANG Y, LONG X, ZHU Y, et al. Air duct design and simulation optimization analysis of air-cooled battery pack[J]. Automotive Engineer, 2020(5): 27-30. |
| [18] |
黄健, 陆嘉伟, 王彦, 等. 某车载医疗方舱风道仿真分析及改进设计[J]. 机械设计与制造工程, 2020, 49(9): 33-37. HUANG J, LU J W, WANG Y, et al. Simulation analysis and improved design of a on-board medical shelter air duct[J]. Machine Design and Manufacturing Engineering, 2020, 49(9): 33-37. |
| [19] |
CIANCIULLI C, WÄTZIG H. Infrared-based temperature measurements in capillary electrophoresis[J]. Electrophoresis, 2011, 32(12): 1530-1536. DOI:10.1002/elps.201000587 |
| [20] |
朱颖谋, 刘智远, 蒋忠城, 等. 基于参数化建模仿真的城轨车辆空调风道送风均匀性优化研究[J]. 技术与市场, 2021, 28(5): 34-36. ZHU Y M, LIU Z Y, JIANG Z C, et al. Optimization of air supply uniformity in air ducts of urban vehicles based on parametric modeling[J]. Technology and Market, 2021, 28(5): 34-36. |




