2. 东南大学 能源热转换及其过程测控教育部重点实验室,江苏 南京 210096
2. Key Laboratory of Energy Thermal Conversion and Control of Ministry of Education, Southeast University, Nanjing 210096, China
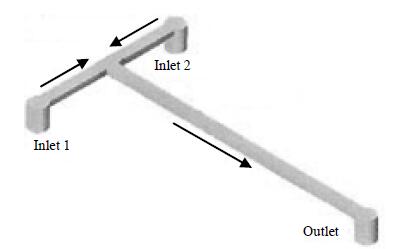
随着微电子机械系统 (MEMS) 的迅速发展,微通道内液-液两相流动得到研究者的广泛关注。常见的两相流动微通道有T型、Y型和十字型等,其中T型微通道作为一种常见的微通道形式,因加工工艺简单,被广泛应用在生物测定、药物输送和微反应器等[1~3]领域,T型微通道内两相流动也成为传热传质领域的热点前沿,具有重要的理论价值和应用前景。
为揭示T型微通道内液-液两相流动的动力学行为,目前已有一定数量的流型演化实验研究报道。Thorse等[4]通过改变两相速度比,在T型微通道内获得了不同的液滴尺寸。Zhao等[5]通过实验对比了不同参数下,T型微通道内液-液两相流流型演化过程。Christopher等[6]探索了不同两相流量比下T型微通道内流型转变规律。这些实验研究结果表明,微通道的几何形状、通道表面和表面特性及其进口流量是影响液-液两相流流型的重要因素。但由于受到实验技术和条件的限制,难以对微通道内液-液两相流流型形成机制及其影响因素等问题进行深入研究。因此,不少学者转而采用计算流体力学方法揭示微流体多相体系的流体动力学行为。尤其格子Boltzmann方法 (Lattice Boltzmann Method, LBM) 因具有准确反映微尺度多相流动界面的介观特性、无需追踪界面[7]、程序设计简单等优点,在微尺度多相流领域得到较为广泛的应用。Kim等[8]和Yu等[9]运用LBM方法模拟了微管中的多相流动,分别探讨了水-油体系中界面张力、水流速度对液滴长度和液滴间距的影响和气-液体系中流体速度、不同通道形状对气泡形成机制的影响。Yang等[10]采用LBM方法模拟获得了微通道内挤压、滴落和喷射三种流动的形成并分析了其影响因素。
然而目前针对T型微通道内液-液两相流型演化的研究仍然非常匮乏,尤其是微通道内的液-液两相流机理及其形貌演化规律需要做深入研究。为此,本文采用格子Boltzmann方法伪势模型,建立T型微通道内的液-液两相流动的理论模型并进行数值模拟,分析了T型微通道内液-液两相流动的流型形成机制及其影响因素,并研究了不同流型下的流场变化。
2 T型微通道内两相流动模型 2.1 格子Boltzmann方法伪势模型与传统计算流体力学方法不同,格子Boltzmann方法基于分子动理论,在时间、空间和速度三方面进行离散。目前LBM方法处理多相流动的模型有:颜色模型、伪势模型[11]、自由能模型及其动理论模型等。由于伪势模型具有原理清晰,自动生成两相界面,易于程序化等优点,本文采用该模型模拟T型微通道内的液-液两相流动。
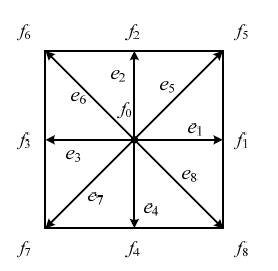
一个完整的格子Boltzmann模型包括三个部分:格子,即离散速度模型 (discrete velocity model, DVM);平衡态分布函数和分布函数的演化方程 (evolution equation)[12]。目前最常用的二维离散速度模型为D2Q9模型 (D代表维数,Q代表离散速度),如图 1所示,相应的速度配置为
|
图 1 D2Q9离散速度模型 Fig.1 Discrete velocity model of D2Q9 |
| ${{e}_{i}}=\left\{ \begin{align} & \begin{matrix} (0,0) & i=0 \\ \end{matrix} \\ & \begin{matrix} c(\cos [(i-1)\frac{\pi }{2}],\sin [(i-1)\frac{\pi }{2}) & i=1,2,3,4 \\ \end{matrix} \\ & \begin{matrix} \sqrt{2}c(\cos [(2i-1)\frac{\pi }{4},\sin (2i-1)\frac{\pi }{4}]) & i=5,6,7,8 \\ \end{matrix} \\ \end{align} \right.$ | (1) |
对于含有S个组分的流体,演化方程包含S个分布函数
| $\begin{matrix} {{f}_{{{k}_{i}}}}(x+{{e}_{i}}\delta t,t+\delta t)={{f}_{{{k}_{i}}}}(x,t)-\frac{1}{\tau }({{f}_{{{k}_{i}}}}(x,t)-f_{{{k}_{i}}}^{eq}(x,t)), & k=1,\cdots ,S \\ \end{matrix}$ | (2) |
这里的演化包含碰撞和迁移两个步骤。
式 (2) 中fkieq为第k类流体的平衡态分布函数
| $f_{{{k}_{i}}}^{eq}={{\rho }_{k}}{{\omega }_{i}}[1+\frac{{{e}_{i}}\cdot u_{k}^{eq}}{c_{s}^{2}}+\frac{{{({{e}_{i}}\cdot u_{k}^{eq})}^{2}}}{2c_{s}^{4}}-\frac{{{(u_{k}^{eq})}^{2}}}{2c_{s}^{2}}]$ | (3) |
上式中,ωi为权系数,在D2Q9速度模型下
| ${{\omega }_{i}}=\left\{ \begin{align} & \begin{matrix} 4/9, & i=0 \\ \end{matrix} \\ & \begin{matrix} 1/9, & i=1,2,3,4 \\ \end{matrix} \\ & \begin{matrix} 1/36, & i=5,6,7,8 \\ \end{matrix} \\ \end{align} \right.$ | (4) |
处理不同相间作用时,Shan和Chen于1993年前后提出,可以通过一个伪势函数反映相间斥力或引力[11, 13~16]。对于流体粒子间作用力,伪势模型假设粒子间存在非局部相互作用,相应势函数为
| ${{V}_{k\bar{k}}}(x,x')={{G}_{k\bar{k}}}(x,x'){{\varphi }_{k}}(x){{\varphi }_{{\bar{k}}}}(x')$ | (5) |
式中,G(x,x’) 为Green函数,表征粒子间相互作用强度,φ(x) 与组分的密度有关,表示组分k的有效密度,一般选取
| ${{\varphi }_{k}}={{\rho }_{k0}}[1-{{e}^{-{{\rho }_{k}}/{{\rho }_{k0}}}}]$ | (6) |
则第k类粒子所受到的粒子间作用力为
| ${{F}_{fk}}(x)=-{{\varphi }_{k}}(x)\sum\limits_{{\bar{k}}}{{{G}_{k\bar{k}}}}\sum\limits_{i}{{{\varphi }_{{\bar{k}}}}(x+{{e}_{i}}\delta t){{e}_{i}}}$ | (7) |
只考虑相邻粒子间作用,在D2Q9模型中,选取
| ${{G}_{k\bar{k}}}=\left\{ \begin{align} & \begin{matrix} G, & \left| {{e}_{i}} \right|=1 \\ \end{matrix} \\ & \begin{matrix} G/4, & \left| {{e}_{i}} \right|=\sqrt{2} \\ \end{matrix} \\ & \begin{matrix} 0, & \left| {{e}_{i}} \right|=0 \\ \end{matrix} \\ \end{align} \right.$ | (8) |
考虑固体表面润湿性对流体流动的影响,流体和固体表面相互作用力Fwk(x) 可用下式表示
| ${{F}_{wk}}(x)=-{{\varphi }_{k}}(x){{G}_{wk}}s(x+{{e}_{i}}){{e}_{i}}$ | (9) |
其中,s的取值表征固相。对于固相区域,其值为l;非固相区域,其值取0。类似地,Gwk是控制流体和固体表面相互作用力强度的参数。通常情况下,对于固体表面,当流体体现为为非润湿性时,Gwk取正值;流体为润湿性流体时,Gwk取负值。
至此,获得作用在流体粒子上的总作用力Fk(x),包括流体之间的相互作用力Ffk(x) 及其流体和固体表面之间的作用力Fwk(x)。在伪势模型中,通过平衡态速度ukeq体现作用力Fk(x) 对流动的影响
| $u_{k}^{eq}(x)=u'(x)+{{\tau }_{k}}\delta t\frac{{{F}_{k}}}{{{\rho }_{k}}}$ | (10) |
式 (10) 中,u'要保证在没有作用力时碰撞过程动量守恒,则
| $u'={}^{\sum\limits_{k}{\frac{{{\rho }_{k}}{{u}_{k}}}{{{\tau }_{k}}}}}\!\!\diagup\!\!{}_{\sum\limits_{k}{\frac{{{\rho }_{k}}}{{{\tau }_{k}}}}}\;$ | (11) |
这里ρk和uk为第k类粒子的密度和速度,且
| ${{\rho }_{k}}=\sum\limits_{i}{{{f}_{{{k}_{i}}}}}$ | (12) |
| ${{\rho }_{k}}{{u}_{k}}=\sum\limits_{k}{{{e}_{i}}{{f}_{{{k}_{i}}}}}$ | (13) |
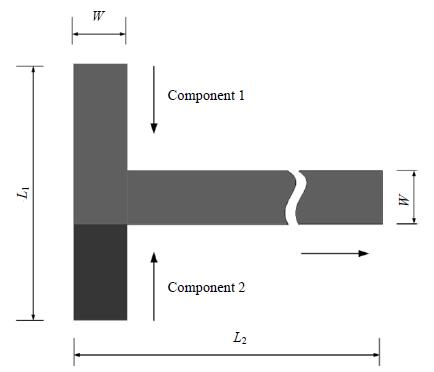
针对Zhao等[5]实验中设计的如图 2所示的T型微通道,本文将其简化为二维模型,数值模拟研究了T型微通道内不同流型的形成机制。参考实验中[5]的通道参数,设计如图 3所示T型微通道,通道宽度W=600 μm,入口总长度L1=3 mm,出口总长度L2=6 mm。两相流体初始化位置如图 3所示,深色区域为1相,即离散相,浅色区域为2相,即连续相。
|
图 3 T型微通道示意图 Fig.3 Schematic diagram of the T-shaped microchannel |
描述微通道内流体流动特性时主要涉及两个参数:两相的韦伯数We和连续相的毛细数Ca,其中,韦伯数We表征流体惯性力与界面张力的相对大小,毛细数Ca为流体黏性力与界面张力的相对大小。
| $We=\frac{\rho {{u}^{2}}l}{\sigma }$ | (14) |
| $Ca=\frac{\mu ul}{\sigma }=\frac{We}{Re}$ | (15) |
式中,σ为两相界面张力系数,μ为流体黏度,u为流体入口流速大小,l为特征尺度 (即取如图 3所示的通道宽度W)。对于本文研究的两相流动体系,Bond数 (表征了流体所受体积力与界面张力的比值) 为Bo=ρgl2 / σ=7.7×10-3 < < 1。由此可知,表面张力克服重力成为控制两相流动力学行为的主要作用力,重力作用可忽略不计[19, 20]。
最后,定义两相组分流量比为q,
| $q=\frac{{{Q}_{2}}}{{{Q}_{1}}}$ | (16) |
其中
| $Q=ul$ | (17) |
为了考察计算区域格子数量对数值模拟结果精确性影响,选取W: 15,L1: 75,L2: 150;W: 18,L1: 90,L2: 180;W: 20,L1: 100,L2: 200及W: 25,L1: 125,L2: 250这四种格子数量分别对二维计算区域的流场进行格子划分,并对比模拟了相同工况不同格子数量下的两相流动流型与界面形貌,如表 1所示。可以看出,随着格子数量的增大,两相界面越清晰,模拟结果趋于收敛,但相应的计算耗时越长。因此,在综合考虑计算精度及计算效率的基础上,本文选取W=20,L1=100,L2=200这套格子数划分本文的计算区域并进行数值模拟。
| 表 1 q=10, Ca=0.31时,不同格子数条件下T型通道内流型对比 Table 1 Comparison of flow regime with different grid numbers under conditions of q=10, Ca=0.31 |
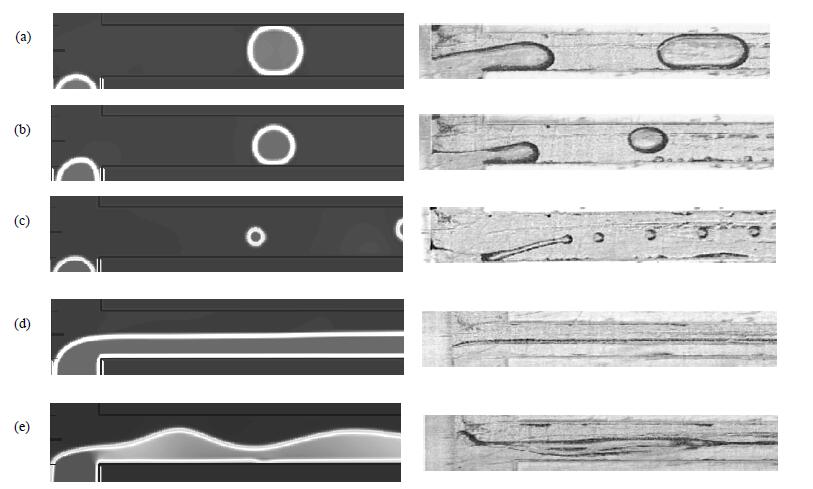
应用格子Boltzmann方法伪势模型,初始化离散相密度ρ1=0.7816,连续相密度ρ2=1.0,T型通道两相入口给定速度,以体现两相的流量比,出口压力恒定。模拟获得T型微通道内液-液两相流的三种经典流型:弹状流 (Slug Flow,SF),滴式流 (Droplet),平行流 (Parallel Flow,PF)。如图 4(a)所示,离散相在下游通道形成弹状流 (Slugs formed at the T-junction (ST),如图 4(a));滴式流,包括单离散液滴流动 (Monodispersed droplets formed at the T-junction (MDT),如图 4(b));液滴群流动 (Drop populations formed in a microchannel (DPM),如图 4(c)) 和平行流动,包括界面稳定的平整平行流 (Parallel flows that have smooth interface formed at the T-junction (PFST),如图 4(d)) 和界面波动的波状平行流 (Parallel flows that have wavy interface formed at the T-junction (PFWT),如图 4(e))。不同工况下数值模拟所得结果 (图 4左) 与实验结果 (图 4右) [5]中的两相流流型基本吻合。
|
图 4 不同参数下T型微通道内液-液两相流流型 Fig.4 Flow patterns in a T-shaped microchannel at different parameters 中文注解 (Parameters in simulation: (a) q=20, We1=1.39×10-3, Ca=0.0889; (b) q=20, We1=5.56×10-3, Ca=0.178; (c) q=40, We1=5.56×10-3, Ca=0.444; (d) q=1, We1=0.556, Ca=0.111; (e) q=1, We1=7.82, Ca=0.417) |
在离散相We数低、两相流量比较高时,两相间的界面张力占主导作用,离散相在下游通道中的形貌呈弹状,即出现弹状流,如图 4 (a)所示。随着两相流速的增加,离散相We数和连续相Ca数增大,离散相在T型微通道内形成液滴,且在两相界面张力的作用下收缩为球形,如图 4(b)及(c)所示。对比图 4(b)与(c)发现,随着连续相Ca数的增大,液滴直径减小。
当两相流量相等时,T型微通道出现平行流。当离散相We数和连续相Ca数较低时,两相界面比较平整,出现平整平行流,如图 4(d)所示。随着两相入口流速的增加,离散相We数和连续相Ca数变大,惯性力对两相流型的影响逐渐占主导地位,两相界面出现波动,但仍能保持界面形貌,最终形成波状平行流动,如图 4(e)所示。
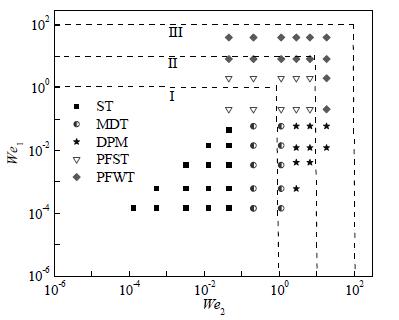
基于数值模拟结果,本文得到与Zhao[5]实验结果类似的流型图,如图 5所示。T型微通道内液-液两相流流型分布与连续相和离散相We数相关,且可分为三个典型区域。区域I内两相We数小于1,两相界面张力起主导作用,离散相在T型微通道内形成弹状或离散液滴,出现弹状流或单离散液滴流动式滴式流;区域II内两相界面张力和惯性力相当,微通道内主要出现液滴群流动式滴式流和平行流,且随着两相We数逐渐增大,即两相流速的增大,惯性力对流型的影响逐渐明显,平行流由平整平行流向波状平行流转变;区域III内两相We数较大,惯性力起主导作用,微通道内主要出现液滴群流动式的滴式流。
|
图 5 T型微通道内流型图 Fig.5 Flow pattern map in the T-shaped microchannel |
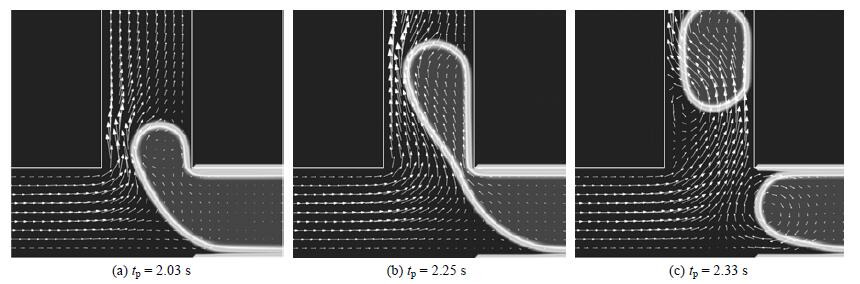
图 6和图 7分别给出了两种参数条件下T型通道交叉处不同时间tp下的速度场矢量图。图 6给出的是两相流量比q较大,且离散相We数较小时T型通道交叉处速度矢量图,初始阶段,离散相开始进入下游通道,由于固体壁面的粘附作用,贴近壁面处的离散相流速小于远离壁面的离散相流速,在离散相前端出现涡流,如图 6(a)所示。离散相进入下游通道后,流速逐渐增大,尤其在通道交叉处离散相在连续相的冲击下,其流速明显大于未进入下游通道的离散相流速,如图 6(b)所示,最终离散相在T型通道交叉处发生断裂,形成弹状流。断裂产生液弹后,入口通道的离散相在两相界面张力的作用下迅速回缩,出现离散相回流现象。由于回流出现在靠近上侧固体壁面处,而靠近下侧固体壁面处离散相仍然向左侧流动,因此形成顺时针方向旋转的涡流,如图 6(c)时刻所示。
|
图 6 q=20, We1=1.39×10-3, Ca=0.0889条件下的速度场 Fig.6 Velocity fields studied under q=20, We1=1.39×10-3, Ca=0.0889 |
|
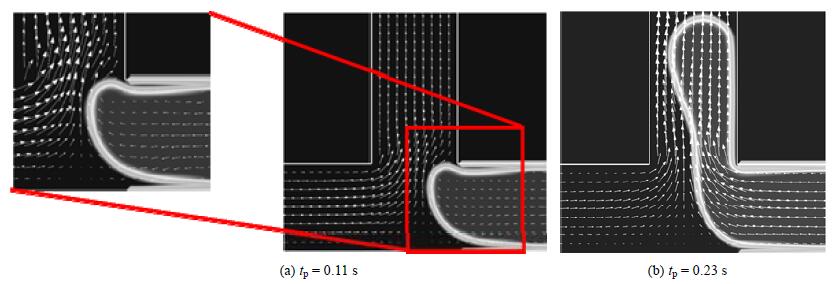
图 7 q=1, We1=0.556, Ca=0.111条件下速度场变化 Fig.7 Velocity field variation under q=1, We1=0.556, Ca=0.111 |
图 7所示为两相流量相等且入口流速较低,出现平行流的工况下,T型通道交叉处的流场变化。与图 6 (a)流场流型类似,初始阶段tp=0.11 s时,贴近壁面的离散相流体速度较小,且在T型通道拐角处出现涡流。随着离散相随连续相流入下游通道,由于两相流量相等,两相流体的流速相近,在两相界面处并无明显的速度梯度。
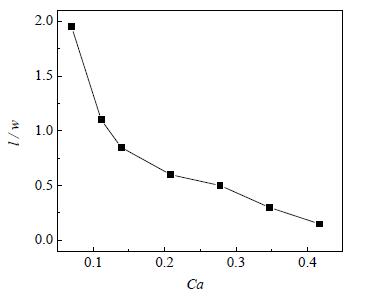
3.3 连续相毛细数Ca对离散相长度的影响以无量纲量l/w表示离散相的相对长度,其中l为离散相沿流动方向的长度,w为微通道宽度。图 8给出了离散相相对长度随连续相毛细数Ca的变化关系图。从图中可知,当Ca数小于约0.12时,l/w > 1,离散相长度较长,形成弹状流,且随着Ca数的增加,离散相相对长度明显减小。当Ca数大于约0.12时,l/w < 1,离散相长度小于通道宽度,在通道内形成液滴,且离散相相对长度随Ca数基本呈线性变化。
|
图 8 离散相相对长度随连续相毛细数Ca的变化 Fig.8 Profile of l/w as a function of Ca |
本文采用格子Boltzmann伪势模型,模拟了T型微通道内液-液两相流动,研究了不同工况下微通道内两相流型的特点及形成机制,主要结论如下:
(1) T型微通道液-液两相流流型受入口流量比和离散相We数的影响,不同工况下出现弹状流、单液滴、液滴群、平整平行流和波状平行流等五种流型。
(2) 离散相We数较小时,两相界面张力起主导作用,离散相易形成弹状流或液滴;界面张力与惯性力相当时,界面张力不足以使离散相形成液滴,通道内两相会形成稳定的平行流动;惯性力占主导时,两相仍平行流动,但界面是否稳定取决于两相入口流速,流速越大界面越难稳定。
(3) 交叉下游的通道内远离通道壁面的离散相流体速度大于近壁面的离散相流速,在离散相前段出现涡流;交叉处离散相流速大于未进入下游通道的离散相流速,出现断裂现象;断裂后,离散相在界面张力作用下回缩,且在前段再次出现涡流。
(4) 离散相相对长度l/w随连续相毛细数Ca增大而减小。毛细数Ca < 0.12时,离散相相对长度变化明显;毛细数Ca > 0.12时,l/w与Ca数基本呈线性关系。
| 符号说明: | |||
| Bo | — 无量纲时间,邦德数 | u’ | — 流体的修正宏观速度,m·s-1 |
| Ca | — 无量纲参数,毛细数 | W | — 通道宽度,m |
| ei | — 离散速度 | We | — 无量纲参数,韦伯数 |
| fki | — k 类组分分布函数 | x | — 位置 |
| fkieq | — k 类组分平衡态分布函数 | δx | — 格子步长 |
| Fk | — k 类粒子所受总作用力 | ||
| Ffk | — k 类粒子所受周围粒子的作用力 | 希腊字母 | |
| Fwk | — k 类粒子所受壁面作用力 | ρ | — 流体的宏观密度,kg·m-3 |
| G | — 流体间作用势 | μ | — 流体黏度,Pa·S |
| Gw | — 流体与固体间作用势 | σ | — 界面张力,N·m-1 |
| l | — 特征长度,m | τ | — 无量纲松弛时间 |
| L | — 通道长度,m | ω | — 权系数 |
| q | — 两组分流量比 | ||
| Q | — 管道内流体流量,m3·s-1 | 上标 | |
| Re | — 无量纲参数,雷诺数 | eq | — 分布函数局部平衡态 |
| t | — 格子时间 | 下标 | |
| tp | — 物理时间,s | i | — 空间离散方向 |
| δt | — 时间步长 | 1, 2, k | — 组分 |
| u | — 流体的宏观速度,m·s-1 |
| [1] | Gunther A, Jensen K F. Multiphase microfluidics:from flow characteristics to chemical and materials synthesis[J]. Lab on a Chip , 2006, 6(12): 1487-1503. DOI:10.1039/B609851G. |
| [2] | Lomel S, Falk L, Commenge J, et al. The microreactor:a systematic and efficient tool for the transition from batch to continuous process[J]. Chemical Engineering Research and Design , 2006, 84(A5): 1-7. |
| [3] | Kiwi-Minsker L, Renken A. Microstructured reactors for catalytic reactions[J]. Catalysis Today , 2005, 110(1-2): 2-14. DOI:10.1016/j.cattod.2005.09.011. |
| [4] | Thorsen T, Roberts R W, Arnold F H, et al. Dynamic pattern formation in a vesicle-generating microfluidic device[J]. Physical Review Letters , 2001, 86(18): 4163-4166. DOI:10.1103/PhysRevLett.86.4163. |
| [5] | Zhao Y C, Chen G W, Yuan Q. Liquid-liquid two-phase flow patterns in a rectangular microchannel[J]. AIChE Journal , 2006, 52(2): 4052-4060. |
| [6] | Christopher G F, Noharuddin N N, Taylor J A, et al. Experimental observations of the squeezing-to-dripping transition in T-shaped microfluidic junctions[J]. Physics Review E , 2008, 78(3): 036317. DOI:10.1103/PhysRevE.78.036317. |
| [7] | Kamali M, Gillissen J, Sundaresan S, et al. Contact line motion without slip in lattice Boltzmann simulations[J]. Chemical Engineering Science , 2011, 66(14): 3452-3458. DOI:10.1016/j.ces.2011.04.010. |
| [8] | Kim L S, Jeong H K, Ha M Y, et al. Numerical simulation of droplet formation in a micro-channel using the lattice Boltzmann method[J]. Journal of Mechanical Science and Technology , 2008, 22(4): 770-779. DOI:10.1007/s12206-007-1201-8. |
| [9] | Yu Z, Hemminger O, Fan L. Experiment and lattice Boltzmann simulation of two-phase gas-liquid flows in microchannels[J]. Chemical Engineering Science , 2008, 62(24): 7172-7173. |
| [10] | Yang H, Zhou Q, Fan L. Three-dimensional numerical study on droplet formation and cell encapsulation process in a micro T-junction[J]. Chemical Engineering Science , 2013, 87(14): 100-110. |
| [11] | Shan X W, Chen H D. Lattice Boltzmann model for simulating flows with multiple phases and components[J]. Physical Review E , 1993, 47(3): 1815-1819. DOI:10.1103/PhysRevE.47.1815. |
| [12] | HE Ya-ling(何雅玲), WANG Yong(王勇), LI Qing(李庆), et al. Lattice boltzmann method:theory and applications(格子Boltzmann方法的理论及应用)[M].Beijing(北京): Science Press(科学出版社), 2009. |
| [13] | Shan X W, He X Y. Discretization of the velocity space in the solution of the Boltzmann equation[J]. Physical Review Letters , 1998, 80(1): 65-68. DOI:10.1103/PhysRevLett.80.65. |
| [14] | Shan X W, Chen H D. Simulation of non-ideal gases and liquid-gas phase transitions by the lattice Boltzmann equation[J]. Physical Review E , 1994, 49(4): 2941-2948. DOI:10.1103/PhysRevE.49.2941. |
| [15] | Shan X W, Doolen G. Diffusion in a multi-component lattice-Boltzmann equation model[J]. Physical Review E , 1996, 54(4): 3614-3620. DOI:10.1103/PhysRevE.54.3614. |
| [16] | He X Y, Doolen G. Thermodynamic foundations of kinetic theory and lattice Boltzmann models for multiphase flows[J]. Journal of Statistical Physics , 2002, 107(1-2): 309-328. |
| [17] | Sauro Succi, et al. The Lattice Boltzmann equation for fluid dynamics and beyond[M].Oxford: Oxford University Press, 2001. |
| [18] | Jonas L. Choice of units in lattice Boltzmann simulations[DB/OL]. Palabos LBM Wiki documentation project, 2008. |
| [19] | GAO Shi-qiao(高世桥), LIU Hai-peng(刘海鹏), et al. Capillary mechanics(毛细力学)[M].Beijing(北京): Science Press(科学出版社), 2010. |
| [20] | Christophe Morel, et al. Mathematical Modeling of Disperse Two-Phase Flows[M].Switzerland: Springer, 2015. |