2. 阿里云智能, 浙江 杭州 311121
2. Alibaba Cloud Intelligence, Hangzhou 311121, China
环氧乙烷(EO)是乙烯工业衍生物中的重要有机化工产品之一,主要用于生产乙二醇,部分用于制造非离子表面活性剂、氨基醇、乙二醇醚等[1]。目前,生产EO的方法主要为乙烯直接氧化法:采用乙烯和氧气为原料,甲烷为稀释和撤热介质,一氯乙烷为反应速率调节剂,各气体通入装填银催化剂的列管式固定床反应器中进行氧化反应,主反应生成EO,副反应生成二氧化碳和水,以及少量乙醛和甲醛。其中,乙烯氧化生成二氧化碳和水的副反应放热量是主反应的12.5倍,因此需要严格控制操作条件,降低副反应发生程度,以避免反应器飞温等事故[2]。由于催化剂在3年生产周期内缓慢失活,为了维持EO产量,反应温度会逐渐提升,各操作条件需定期调整。确定各操作条件的影响和催化剂的活性变化,对提升装置安全性和经济效益有重要意义。
目前,研究者对反应过程进行了许多研究,包括分析乙烯在催化剂上的氧化机理[3-4]、氯化物对选择性的影响[5-6],并提出了各种反应动力学模型[7-10]和催化剂失活速率方程[7, 11]。此外,研究者采用不同的反应器模型(一维和二维、均相和非均相等)模拟实际生产过程[12-17],根据模拟结果提出对应的操作优化策略[18-21]。由于催化剂反应机理和失活机理的复杂性,机器学习模型例如人工神经网络(ANN)、支持向量回归(SVR)等这类无需机理的方法也被应用于催化建模中。例如Chowdhury等[22]根据EO工厂的生产数据,利用ANN建立了催化剂工作时间、各操作参数与选择性、温度的关系。Lahiri等[23]利用实际生产数据,通过SVR建立了催化剂工作时间、各操作参数与产物产量、选择性的关系。Luo等[24]建立了包含先验知识的SVR失活模型,用于计算催化剂失活速率,将反应动力学、SVR失活模型和反应器模型集成到混合模型中,EO产量预测误差小于5%。与ANN相比,SVR是一种基于结构风险最小化的机器学习方法,有较好的预测精度和泛化能力,适用于小样本、高维、非线性问题的研究[25]。
由于不同的催化剂反应动力学参数和失活速率各不相同,以及反应器内存在复杂的相互作用,有必要通过实际生产数据建立过程模型。本研究对某工业EO反应器的生产数据进行了深度分析,分别利用机理模型和SVR建立EO生产预测模型,并对两种模型进行了比较。模型中考虑了各操作条件的影响和催化剂的活性变化,为优化操作条件、提高选择性提供了基础。
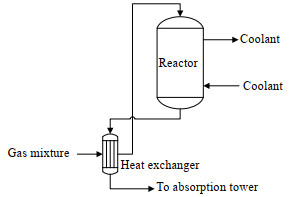
2 机理模型 2.1 反应工段如图 1所示,进料混合气通过换热器与反应器出口气体进行换热,预热后的进料气体通过装有催化剂的列管式反应器,在催化剂床层发生氧化反应,放出的热量由冷却剂蒸发移走。反应器出口气体通入换热器冷却后,进入吸收塔。表 1为某EO工厂反应器装置参数与操作参数。
|
图 1 反应工段流程图 Fig.1 Flowsheet of reaction section |
|
|
表 1 某EO工厂反应器装置参数与操作参数 Table 1 Reactor device parameters and operating parameters of an EO plant |
反应器内的主反应为:
| $ {\text{2}}{{\text{C}}_{\text{2}}}{{\text{H}}_{\text{4}}}{\text{ + }}{{\text{O}}_{\text{2}}} \to {\text{2}}{{\text{C}}_{\text{2}}}{{\text{H}}_{\text{4}}}{\text{O}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \Delta H= - {105.3_{}}{\text{kJ}} \cdot {\text{mo}}{{\text{l}}^{ - 1}} $ | (1) |
副反应包括:
| $ {{\text{C}}_{\text{2}}}{{\text{H}}_{\text{4}}}{\text{ + 3}}{{\text{O}}_{\text{2}}} \to {\text{2C}}{{\text{O}}_{\text{2}}}{\text{ + 2}}{{\text{H}}_{\text{2}}}{\text{O}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \Delta H= - {1_{}}{320.5_{}}{\text{kJ}} \cdot {\text{mo}}{{\text{l}}^{ - 1}} $ | (2) |
| $ {{\text{C}}_{\text{2}}}{{\text{H}}_{\text{4}}}{\text{O + 2}}{\text{.5}}{{\text{O}}_{\text{2}}} \to {\text{2C}}{{\text{O}}_{\text{2}}}{\text{ + 2}}{{\text{H}}_{\text{2}}}{\text{O}}{\kern 1pt} $ | (3) |
| $ {{\text{C}}_{\text{2}}}{{\text{H}}_{\text{4}}}{\text{ + 0}}{\text{.5}}{{\text{O}}_{\text{2}}} \to {\rm{C}}{{\rm{H}}_{\rm{3}}}{\rm{CHO}} $ | (4) |
| $ {{\text{C}}_{\text{2}}}{{\text{H}}_{\text{4}}}{\text{ + }}{{\text{O}}_{\text{2}}} \to {\text{2C}}{{\text{H}}_2}{O} $ | (5) |
| $ {{\text{C}}_{\text{2}}}{{\text{H}}_{\text{4}}}{\text{O}} \to {\rm{C}}{{\rm{H}}_{\rm{3}}}{\rm{CHO}} $ | (6) |
| $ {\rm{C}}{{\rm{H}}_{\rm{3}}}{\rm{CHO}} + 2{\rm{O}_2} \to {\text{2C}}{{\text{O}}_{\text{2}}}{\text{ + }}{{\text{H}}_{\text{2}}}{\text{O}}{\kern 1pt} $ | (7) |
实际生产条件下副反应式(3)~(7)的反应速率很小,CH3CHO和CH2O量很少,反应产物主要是EO、CO2和H2O,因此所建立的机理模型仅考虑式(1)和式(2)。反应器内的气体包括C2H4、O2、EO、CO2、H2O、CH4、N2、C2H5Cl,以产物EO和CO2作为关键组分衡算可得:
主反应式(1)进度
| $ {{\eta _1}}{\text{=}}0.5(N{y_\rm{EO}} - {N_\rm{in}}{y_\rm{EO,\rm{in}}}) $ | (8) |
副反应式(2)进度
| $ {\eta _2}{\text{=}}0.5(N{y_\rm{C\rm{O_2}}} - {N_\rm{in}}{y_\rm{C\rm{O_2},\rm{in}}}) $ | (9) |
由式(1)和式(2)左右两边的化学计量数可知,主反应O2物质的量消耗量即为混合气物质的量减少值,可得:
| $ N={N_\rm{in}} - 0.5(N{y_\rm{EO}} - {N_\rm{in}}{y_\rm{EO,\rm{in}}})={N_\rm{in}}\frac{{(2 + {y_\rm{EO,\rm{in}}})}}{{(2 + {y_\rm{EO}})}} $ | (10) |
通过物料衡算可得:
| $ {y_\rm{{C_2}{H_4}}}=\frac{{{N_\rm{in}}{y_\rm{{C_2}{H_4},\rm{in}}} - 2{{\eta _1}} - {\eta _2}}}{N}=\frac{{(2 + {y_\rm{EO}})}}{{(2 + {y_\rm{EO,\rm{in}}})}}({y_\rm{{C_2}{H_4},\rm{in}}} + {y_\rm{EO,\rm{in}}} + 0.5{y_\rm{C\rm{O_2},\rm{in}}}) - {y_\rm{EO}} - 0.5{y_\rm{C\rm{O_2}}} $ | (11) |
| $ {y_{\rm{O_2}}}=\frac{{{N_\rm{in}}{y_{\rm{O_2},\rm{in}}} - {{\eta _1}} - 3{\eta _2}}}{N}=\frac{{(2 + {y_\rm{EO}})}}{{(2 + {y_\rm{EO,\rm{in}}})}}({y_{\rm{O_2},\rm{in}}} + 0.5{y_\rm{EO,\rm{in}}} + 1.5{y_\rm{C\rm{O_2},\rm{in}}}) - 0.5{y_\rm{EO}} - 1.5{y_\rm{C\rm{O_2}}} $ | (12) |
| $ {y_\rm{{H_2}O}}=\frac{{{N_\rm{in}}{y_\rm{{H_2}O,\rm{in}}} + 2{\eta _2}}}{N}=\frac{{(2 + {y_\rm{EO}})}}{{(2 + {y_\rm{EO,\rm{in}}})}}({y_\rm{{H_2}O,\rm{in}}} - {y_\rm{C\rm{O_2},\rm{in}}}) + {y_\rm{C\rm{O_2}}} $ | (13) |
| $ {y_\rm{C{H_4}}}=\frac{{{N_\rm{in}}{y_\rm{C{H_4},\rm{in}}}}}{N}={y_\rm{{C}{{H}_4},\rm{in}}}\frac{{(2 + {y_{\rm{EO}}})}}{{(2 + {y_{\rm{EO},\rm{in}}})}} $ | (14) |
| $ {y_\rm{{{N}_2}}}=\frac{{{N_{\rm{in}}}{y_\rm{{{N}_2},\rm{in}}}}}{N}={y_\rm{{{N}_2},\rm{in}}}\frac{{(2 + {y_{\rm{EO}}})}}{{(2 + {y_{\rm{EO,\rm{in}}}})}} $ | (15) |
| $ {y_\rm{{{C}_{2}}{{H}_{5}}{Cl}}}=\frac{{{N_{\rm{in}}}{y_\rm{{{C}_{2}}{{H}_{5}}{Cl,\rm{in}}}}}}{N}={y_\rm{{{C}_{2}}{{H}_{5}}{Cl,\rm{in}}}}\frac{{(2 + {y_{\rm{EO}}})}}{{(2 + {y_{\rm{EO,\rm{in}}}})}} $ | (16) |
因商业原因,本研究涉及的催化剂性能尚无文献报道。根据文献[8]汇总的多种反应动力学方程,采用式(17)~(19)计算反应速率,本研究通过生产数据回归其动力学参数。
主反应式(1)速率
| $ {r_1}= - \frac{{{\text{d}}{N_{{{\text{C}}_{\text{2}}}{{\text{H}}_{\text{4}}}{\text{,1}}}}}}{{{\text{d}}{W_{{\text{cat}}}}}}=\frac{{{k_1}{p_{{{\text{C}}_{\text{2}}}{{\text{H}}_{\text{4}}}}}{p_{{{\text{O}}_{\text{2}}}}}}}{{1 + {K_1}{p_{{\text{C}}{{\text{O}}_{\text{2}}}}} + {K_2}p_{_{{{\text{O}}_{\text{2}}}}}^{0.5}{p_{{{\text{H}}_{\text{2}}}{\text{O}}}}}} \times \frac{1}{{1 + {K_3}{y_{{{\text{C}}_{\text{2}}}{{\text{H}}_{\text{5}}}{\text{Cl}}}}}} $ | (17) |
副反应式(2)速率
| $ {r_2}= - \frac{{{\text{d}}{N_{{{\text{C}}_{\text{2}}}{{\text{H}}_{\text{4}}}{\text{,2}}}}}}{{{\text{d}}{W_{{\text{cat}}}}}}=\frac{{{k_2}{p_{{{\text{C}}_{\text{2}}}{{\text{H}}_{\text{4}}}}}p_{_{{{\text{O}}_{\text{2}}}}}^{{k_3}}}}{{1 + {K_1}{p_{{\text{C}}{{\text{O}}_{\text{2}}}}} + {K_2}p_{_{{{\text{O}}_{\text{2}}}}}^{0.5}{p_{{{\text{H}}_{\text{2}}}{\text{O}}}}}} \times \frac{1}{{1 + {K_4}{y_{{{\text{C}}_{\text{2}}}{{\text{H}}_{\text{5}}}{\text{Cl}}}}}} $ | (18) |
| $ {p_i}={y_i}p $ | (19) |
固定床反应器的压降采用Ergun方程计算[20],其中A和B为待拟合参数,利用实际压降数据拟合。
| $ \frac{{dp}}{{dZ}}=A{\mu _m}{v_s} + B{\rho _{m}}v_{s}^2 $ | (20) |
| $ {v_s}=\frac{{4NRT}}{{p{\text{π }}d_{\text{I}}^2n}} $ | (21) |
| $ {\rho _m}=\frac{{p\sum {{y_i}{M_i}} }}{{RT}} $ | (22) |
混合气的黏度μm使用式(23)~(25)计算:
| $\mu_{\mathrm{m}}=\sum\limits_i \frac{\mu_i}{1+\frac{1}{y_i} \sum\limits_{\substack{j=1 \\ j \neq i}} y_j \phi_{ij}}$ | (23) |
| $ {\phi _{ij}}=\frac{{{{[1 + {{({\mu _i}/{\mu _j})}^{0.5}}{{({M_j}/{M_i})}^{0.25}}]}^2}}}{{(4/\sqrt 2 ){{[1 + ({M_i}/{M_j})]}^{0.5}}}} $ | (24) |
| $ {\mu _i}=\frac{{{a_i} \cdot {T^{{b_i}}}}}{{1 + {c_i}/T + {d_i}/{T^2}}} $ | (25) |
其中ai,bi,ci,di为黏度经验公式系数,如表 2所示。
|
|
表 2 计算气体黏度的参数 Table 2 Parameters for calculating gas viscosity |
催化剂的活性在生产过程中会缓慢衰减,根据参考文献的研究,催化剂的失活速率与催化剂使用时间和冷却剂温度(即副产蒸汽的气包温度)相关[7],冷却剂温度可以反映反应器内的温度状况,采用式(26)~(27)计算失活速率:
| $ - \frac{{{\text{d}}{a_1}}}{{{\text{d}}t}}={k_{{d},1}}\exp ( - \frac{{{E_{a,{d},1}}}}{{R{T_{w,t}}}}){a_1}^{{d_1}},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {{a_1}} \right|{{\kern 1pt} _{t=0}}=1{\kern 1pt} $ | (26) |
| $ - \frac{{{\text{d}}{a_2}}}{{{\text{d}}t}}={k_{{d},2}}\exp ( - \frac{{{E_{a,{d},2}}}}{{R{T_{w,t}}}}){a_2}^{{d_2}},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {{a_2}} \right|{{\kern 1pt} _{t=0}}=1{\kern 1pt} $ | (27) |
积分可得到:
| $a_1(t)=\left\{\begin{array}{l} {\left[1-\left(1-d_1\right) \int_0^t k_{\mathrm{d}, 1} \exp \left(-\frac{E_{a, \mathrm{~d}, 1}}{R T_{\mathrm{w}, t}}\right) \mathrm{d} t\right]^{\frac{1}{1-d_1}}, \quad d_1 \neq 1} \\ \exp \left(-\int_0^t k_{\mathrm{d}, 1} \exp \left(-\frac{E_{a, \mathrm{~d}, 1}}{R T_{\mathrm{w}, t}}\right) \mathrm{d} t\right), \quad d_1=1 \end{array}\right.$ | (28) |
| $a_2(t)=\left\{\begin{array}{l} {\left[1-\left(1-d_2\right) \int_0^t k_{\mathrm{d}, 2} \exp \left(-\frac{E_{a, \mathrm{~d}, 2}}{R T_{\mathrm{w}, t}}\right) \mathrm{d} t\right]^{\frac{1}{1-d_2}}, \quad d_2 \neq 1} \\ \exp \left(-\int_0^t k_{\mathrm{d}, 2} \exp \left(-\frac{E_{a, \mathrm{~d}, 2}}{R T_{\mathrm{w}, t}}\right) \mathrm{d} t\right), \quad d_2=1 \end{array}\right.$ | (29) |
考虑到固定床反应器中雷诺数Re=Gdp/μm > 40,催化剂床层高度与颗粒当量直径之比L/dp远大于150,催化剂床层与壳程冷却剂温差不大,本研究采用一维拟均相平推流反应器模型[12],忽略径向和轴向的导热和扩散,计算反应器出口各组分组成。
| $ \frac{{{\text{d}}(N{y_{\rm{EO}}})}}{{{\text{d}}Z}}=(\frac{{\text{π }}}{4}d_{\text{I}}^2n){\rho _{B}}{r_1}{a_1} $ | (30) |
| $ \frac{{{\text{d}}(N{y_\rm{{C}{{O}_2}}})}}{{{\text{d}}Z}}=(\frac{{\text{π }}}{4}d_{\text{I}}^2n){\rho _{B}}(2{r_2}){a_2} $ | (31) |
| $ \frac{{{\text{d}}(G{c_{p,m}}T)}}{{{\text{d}}Z}}={\rho _B}[{r_1}( - \Delta {H_1}) + {r_2}( - \Delta {H_2})] - \frac{{4U}}{{{d_{\text{I}}}}}(T - {T_{w}}) $ | (32) |
其中比热容cp, m和总传热系数U的计算参考相关文献[26]。
2.5 数据处理与模型建立阿里云自主研发的工业智能制造平台(AICS)可以方便地集成第三方数采和控制系统,提供了丰富的数据处理和机器学习模块,支持自定义模型,研究人员通过简单的操作和少量的代码即可快速搭建模型[27]。本研究使用AICS平台进行数据处理和建模预测:
(1) 采集了某EO工厂催化剂投入使用后一年内的反应器生产数据,采样间隔为10 s,机理模型所使用的输入数据为进料质量流量、入口温度、入口压力、C2H4入口浓度(摩尔分数,下同)、O2入口浓度、EO入口浓度、CO2入口浓度、CH4入口浓度、N2入口浓度、C2H5Cl入口浓度、冷却剂温度、冷却剂流量;输出数据为C2H4出口浓度、O2出口浓度、EO出口浓度、CO2出口浓度、反应选择性。
(2) 采集的数据中存在部分异常值,需要进行剔除,以避免对模型造成不良影响。识别异常数据的常用方法有三倍标准差和四分位数法。四分位数法不需要数据服从正态分布,识别异常数据依赖于第一四分位数(Q1)和第三四分位数(Q3),极端异常值并不会影响Q1和Q3,这一点要优于三倍标准差法。因此,使用四分位数法识别异常数据:将每列数据按从小到大排列,第25% 的数据即为Q1,第75% 的数据即为Q3,四分位距QIQR=Q3−Q1,数据上界为Q3+1.5×QIQR,数据下界为Q1−1.5×QIQR,大于上界或者小于下界的数据判断为异常生产数据。
(3) 由于机理模型中催化剂活性按天计算,且每天各采样间隔的生产数据变化很小,因此将各采样间隔的生产数据按天取平均值,获得了每天的平均生产数据。同时将生产日期编号为催化剂运行天数,作为自变量。
(4) 划分训练集和测试集:由于催化剂的活性和生产数据随时间变化,因此按运行天数取前70% 的数据作为训练集,用于回归模型参数,后30% 的数据作为测试集,检验模型的外推能力。
(5) 使用Python语言编写了反应器机理模型的计算程序,其中常微分方程组通过Scipy科学计算库的ode模块进行求解,催化剂床层轴向离散点数为20 000(当离散点数超过20 000时,计算结果几乎不变)。采用最小二乘法拟合参数:通过序贯二次规划算法(SQP)使出口组成实际值和计算值的误差平方和最小,该算法所使用的参数初始值参考相关文献[7-8]。
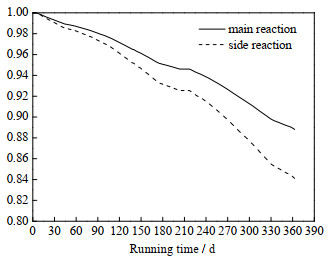
2.6 模拟结果与验证最终在训练集上拟合所得动力学参数
|
图 2 计算所得的催化剂活性变化 Fig.2 Calculated values of catalyst activity variation |
本研究采用平均绝对误差(SMAE)和平均绝对百分比误差(SMAPE)来评估模型在训练集和测试集上的准确性,如式(33)~(34),误差越小,则模型的预测效果越好。
| $S_{\mathrm{MAE}}=\frac{1}{m} \sum\limits_{k=1}^m\left|y_{\mathrm{act}, k}-y_{\mathrm{cal}, k}\right|$ | (33) |
| $S_{\mathrm{MAPE}}=\frac{1}{m} \sum\limits_{k=1}^m \frac{\left|y_{\mathrm{act}, k}-y_{\mathrm{cal}, k}\right|}{y_{\mathrm{act}, k}}$ | (34) |
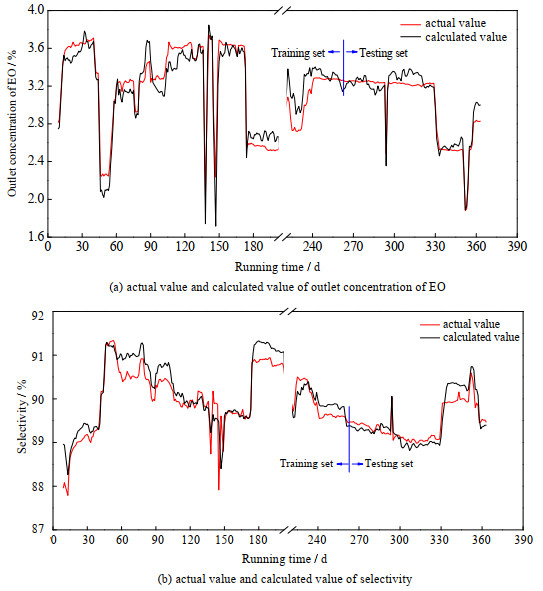
表 3是机理模型计算所得的反应器出口各组分浓度和选择性与实际值的误差,在训练集上各输出变量的SMAE小于0.3%,SMAPE小于5%,说明机理模型的训练效果良好。在测试集上SMAE小于0.3%,而SMAPE小于3%,可见机理模型的外推能力良好。图 3展示了机理模型计算的各运行时间反应器出口EO浓度和选择性与实际值对比情况,可以看到实际值和计算值对应的曲线较为接近。
|
|
表 3 机理模型的误差值 Table 3 Errors of mechanism model |
|
图 3 实际值与机理模型计算值的对比 Fig.3 Comparison between actual values and calculated values of mechanism model |
考虑线性回归问题:给定样本集{(x1, y1), (x2, y2), …, (xm, ym)},其中xi和yi分别为输入数据和输出数据,m为样本数,SVR希望回归一个超平面
| $\begin{aligned} \min _{\boldsymbol{w}, b, {\xi}_i, \hat{\xi}_i} & \frac{1}{2}\|\boldsymbol{w}\|^2+C \sum\limits_{i=1}^m\left(\xi_i+\hat{\xi}_i\right) \\ \text { s.t. } & f\left(\boldsymbol{x}_i\right)-y_i \leqslant \epsilon+\xi_i \\ & y_i-f\left(\boldsymbol{x}_i\right) \leqslant \epsilon+\hat{\xi}_i \\ & \xi_i \geqslant 0, \hat{\xi}_i \geqslant 0, \quad i=1,2, \ldots, m \end{aligned}$ | (35) |
式中:C为惩罚项系数;
| $\begin{aligned} \max _{\alpha_i, \hat{\alpha}_i} & \sum\limits_{i=1}^m y_i\left(\hat{\alpha}_i-\alpha_i\right)-\epsilon\left(\hat{\alpha}_i+\alpha_i\right)-\frac{1}{2} \sum\limits_{i=1}^m \sum\limits_{j=1}^m\left(\hat{\alpha}_i-\alpha_i\right)\left(\hat{\alpha}_j-\alpha_j\right) \boldsymbol{x}_i^{\mathrm{T}} \boldsymbol{x}_j \\ & { s.t. }\;\;\; \sum\limits_{i=1}^m\left(\hat{\alpha}_i-\alpha_i\right)=0,0 \leqslant \alpha_i, \hat{\alpha}_i \leqslant C \end{aligned}$ | (36) |
解出
| $ f(\boldsymbol{x})=\sum\limits_{i=1}^m {({{\hat \alpha }_i} - {\alpha _i})\boldsymbol{x}_i^\rm{T}\boldsymbol{x} + b} $ | (37) |
对于非线性回归问题,超平面模型不适合直接使用,可以通过一个特征映射
| $ f(x)={\displaystyle \sum _{i=1}^{m}({\widehat{\alpha }}_{i}-{\alpha }_{i})f{(\boldsymbol{x}_{i})}^\rm{T}f(\boldsymbol{x})+b} $ | (38) |
由于特征映射和内积运算较为复杂,实际中使用核函数
| $ f(\boldsymbol{x})=\sum\limits_{i=1}^m {({{\hat \alpha }_i} - {\alpha _i})\kappa (\boldsymbol{x},{\boldsymbol{x}_i}) + b} $ | (39) |
对于式(36)的凸二次规划问题,由于问题规模正比于样本数,使用通用的优化算法求解较为低效。SVR采用序列最小最优化算法(SMO)进行求解:每次选择两个变量,固定其他变量,对二次规划子问题进行解析求解,直到所有变量满足KKT条件(Karush–Kuhn–Tucker conditions)为止。虽然计算子问题次数很多,但每个子问题计算很快,算法总体上很高效。
3.2 数据处理和模型建立(1) 数据采集、异常数据处理和数据集划分方法与机理模型相同,输入变量中也包含催化剂使用时间。
(2) 由于不同的变量数值相差较大,为了消除数据量纲的影响,采用如式(40)的归一化方法将每列数据映射到[0, 1]:
| $ {x_i}=\frac{{{x_i} - {x_{\min }}}}{{{x_{\max }} - {x_{\min }}}} $ | (40) |
(3) 传统的SVR模型仅支持回归单输出变量,无法回归多输出变量。为了实现回归多输出变量,可采用两种方法:(a)假设每个输出变量相互独立,为每个输出变量训练单独的SVR模型;(b)创建模型回归序列:第一个SVR模型使用输入预测得到一个输出,第二个SVR模型使用输入和第一个模型的输出预测第二个输出,第三个SVR模型使用输入和前2个模型的输出预测第三个输出,以此类推。由于各输出变量相互关联,本研究使用方法(b)实现SVR回归多输出变量。考虑到各个输出变量的波动大小,回归序列依次为EO出口浓度、C2H4出口浓度、O2出口浓度、CO2出口浓度和选择性。
(4) 设置SVR模型的超参数,包括核函数的类型、惩罚项系数C和容忍偏差∈。本研究选择高斯核函数,通过网格搜索法寻找最优的系数C和偏差∈。
(5) 为了充分利用样本数据,在训练集上采用10次10折交叉验证的方法进行训练和超参数的选择:将训练集数据随机划分为10等份,每次选择1份作为验证集,其余数据用于模型训练,对10种选择重复进行训练,最后选出在10次评测中平均验证误差最小的模型。
3.3 模拟结果对比分别取C为0.05~1.00中的20个数(间隔为0.05),取容忍偏差∈为0.000 1~0.002 0中的20个数(间隔为0.000 1),共训练了400个不同参数的模型。当C=0.55和∈=0.000 4时,模型的平均验证误差最小,故选择该参数组合为SVR的超参数。
表 4是SVR模拟的反应器出口各组分浓度和选择性的误差值,在训练集上各输出变量SMAE小于0.5%,而SMAPE小于5%,在测试集上SMAE小于0.4%,而SMAPE小于5%。对比表 3和表 4可以看到,与机理模型相比,SVR预测CO2、EO浓度和选择性的误差相对偏小,而预测C2H4、O2浓度的误差相对偏大,说明SVR模型不能完全替代机理模型。如果需要更准确预测各个组分的出口浓度和选择性,结合机理模型和SVR进行预测会是一个更合理的方法。
|
|
表 4 SVR模型的误差值 Table 4 Errors of SVR model |
从式(28)~(29)可以看出催化剂的活性不仅仅与催化剂使用时间相关,还与之前的操作条件有关。上述SVR模型仅以催化剂使用时间和当前操作条件作为输入变量进行预测,可能不足以反映真实情况,因此有必要在输入变量中添加反映过去时间段操作条件的变量。如果采用时间序列模型的方法,将过去一段时间的输入变量和输出变量添加到当前时间的输入变量中,又会使得输入变量维度显著增大,训练较为困难。因此,本研究选择将机理模型计算所得的主反应活性变量和副反应活性变量(图 2)添加到SVR模型的输入变量中,重新进行训练。式(28)~(29)的参数是通过训练集拟合所得,测试集上的活性变量是通过冷却剂温度(输入变量)计算所得,因此不会引入额外的变量。
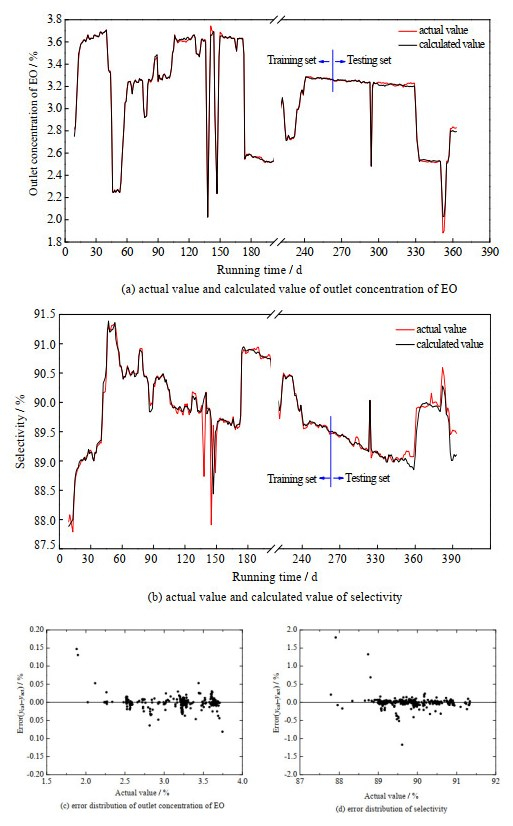
同样按照10次10折交叉验证和网格搜索法寻找最佳超参数,最终确定的超参数为C=0.80和∈=0.001 2。表 5是加入活性变量的SVR模拟的出口各组分组成和选择性的误差值,在训练集和测试集上各输出变量的误差均小于原始SVR模型的误差,在测试集上SMAE小于0.4%,而SMAPE小于3%,与机理模型相比,除C2H4出口浓度外,各输出变量的误差值更小,可见引入了机理知识的数据模型具有较好的预测精度和泛化能力。加入活性变量的SVR模型各运行时间的计算值与实际值的对比如图 4所示,可以看到实际值和计算值对应的曲线非常接近。偏差分布图也显示正负偏差分布合理,且偏差绝对值较小。
|
|
表 5 加入活性变量的SVR模型的误差值 Table 5 Errors of SVR model with activity variables |
|
图 4 实际值与加入活性变量的SVR模型计算值对比 Fig.4 Comparison between actual values and calculated values of SVR model with activity variables |
本研究通过工业生产数据建立EO反应器模型,分别利用机理模型和SVR确定了催化剂使用时间、各操作条件和反应器出口组成的关系,通过机理模型获取了催化剂失活速率。将机理模型计算所得的活性变量添加到SVR的输入变量中,使模型可以考虑催化剂的活性变化,所得模型在训练集和测试集上的各项误差均小于原始模型,说明引入机理知识的数据模型具有较好的预测精度和泛化能力。
符号说明: a1
⎯ 催化剂主反应活性
p
⎯ 反应器的压力,MPa a2
⎯ 催化剂副反应活性
pi
⎯ 反应器中组分i的分压,MPa cp, m
⎯ 混合气的定压比热容,J⋅kg−1⋅K−1
R
⎯ 气体常数,8.314 J⋅mol−1⋅K−1 dI
⎯ 反应器列管内径,m
r1
⎯ 主反应的反应速率,mol⋅g−1⋅h−1 d1
⎯ 主反应失活速率方程的指数
r2
⎯ 副反应的反应速率,mol⋅g−1⋅h−1 d2
⎯ 副反应失活速率方程的指数
T
⎯ 混合气的温度,K Ea, d, 1
⎯ 主反应失活速率方程的活化能,J⋅mol−1
Tw
⎯ 壳程冷却剂的温度,K Ea, d, 2
⎯ 副反应失活速率方程的活化能,J⋅mol−1
Tw, t
⎯ 时间为t的壳程冷却剂的温度,K G
⎯ 混合气的质量流速,kg⋅h−1⋅m−2
t
⎯ 催化剂使用时间,d ΔH1
⎯ 主反应焓变,kJ⋅mol−1
U
⎯ 总传热系数,W⋅m−2⋅K−1 ΔH2
⎯ 副反应焓变,kJ⋅mol−1
vs
⎯ 混合气流速,m⋅s−1 K1
⎯ CO2吸附平衡常数
Wcat
⎯ 催化剂装填质量,kg K2
⎯ O2吸附平衡常数
xmax
⎯ 每列数据的最大值 K3
⎯ C2H5Cl吸附平衡常数
xmin
⎯ 每列数据的最小值 k1
⎯ 主反应速率常数
yact, k
⎯ 第k个样本的实际值 k2
⎯ 副反应速率常数
ycal, k
⎯ 第k个样本的计算值 k3
⎯ O2的反应级数
yi
⎯ 反应器轴向某位置组分i的摩尔分数 kd, 1
⎯ 失活速率常数
yi, in
⎯ 反应器入口组分i的摩尔分数 kd, 2
⎯ 失活速率常数
Z
⎯ 反应器轴向位置,m Mi
⎯ 组分i的摩尔质量,g⋅mol−1
η1
⎯ 主反应进度,kmol⋅h−1 m
⎯ 样本个数
η2
⎯ 副反应进度,kmol⋅h−1 N
⎯ 反应器轴向某位置混合气的摩尔流量,kmol⋅h−1
μi
⎯ 组分i的黏度,Pa⋅s NC2H4, 1
⎯ 主反应的乙烯消耗速率,kmol⋅h−1
μm
⎯ 混合气的黏度,Pa⋅s NC2H4, 2
⎯ 副反应的乙烯消耗速率,kmol⋅h−1
ρB
⎯ 催化剂堆积密度,kg⋅m−3 NC2H5, Cl
⎯ C2H5Cl的摩尔分数,10−6
ρi
⎯ 组分i的密度,kg⋅m−3 Nin
⎯ 反应器入口混合气的摩尔流量,kmol⋅h−1
ρm
⎯ 混合气的密度,kg⋅m−3 n
⎯ 反应器列管个数
ϕij
⎯ 组分i和组分j的二元交互参数
| [1] |
杨宝娟, 王晓军, 于梅, 等. 我国环氧乙烷市场分析及研发进展[J]. 化学工业, 2020, 38(2): 52-57, 62. YANG B J, WANG X J, YU M, et al. Market analysis and technical development of ethylene oxide in China[J]. Chemical Industry, 2020, 38(2): 52-57, 62. |
| [2] |
黄仲九, 房鼎业. 化学工艺学[M]. 北京: 高等教育出版社, 2011: 82-92. HUANG Z J, FANG D Y. Chemical technology[M]. Beijing: Higher Education Press, 2011: 82-92. |
| [3] |
CARBONIO E A, ROCHA T C R, KLYUSHIN A Y, et al. Are multiple oxygen species selective in ethylene epoxidation on silver?[J]. Chemical Science, 2018, 9(4): 990-998. |
| [4] |
PU T C, TIAN H J, FORD M E, et al. Overview of selective oxidation of ethylene to ethylene oxide by Ag catalysts[J]. ACS Catalysis, 2019, 9(12): 10727-10750. |
| [5] |
ROCHA T C R, HÄVECKER M, KNOP-GERICKE A, et al. Promoters in heterogeneous catalysis: The role of Cl on ethylene epoxidation over Ag[J]. Journal of Catalysis, 2014, 312: 12-16. |
| [6] |
HARRIS J W, BHAN A. Moderation of chlorine coverage and ethylene epoxidation kinetics via ethane oxychlorination over promoted Ag/α-Al2O3[J]. Journal of Catalysis, 2018, 367: 62-71. |
| [7] |
甘霖, 王弘轼, 朱炳辰, 等. 环氧乙烷合成银催化剂宏观动力学及失活分析[J]. 化工学报, 2001, 52(11): 969-973. GAN L, WANG H S, ZHU B C, et al. Global kinetics and deactivation of silver catalyst for ethylene oxide synthesis[J]. CIESC Journal, 2001, 52(11): 969-973. |
| [8] |
梁汝军. YS-7型银催化剂上乙烯环氧化宏观动力学研究[D]. 北京: 北京化工大学, 2006. LIANG R J. Study on macrokinetics of ethylene epoxidation over YS-7 silver catalyst [D]. Beijing: Beijing University of Chemical Technology, 2006. |
| [9] |
DELAVAR H, NADERIFAR A. Kinetic model of ethylene oxidation in the presence of both ethylene dichloride (1, 2-dichloroethane) and carbon dioxide over a highly selective silver catalyst[J]. Chemical Engineering Science, 2022, 250: 117425. DOI:10.1016/j.ces.2022.117425 |
| [10] |
文启星. 乙烯环氧化制环氧乙烷的微观和宏观反应动力学研究[D]. 北京: 北京化工大学, 2022. WEN Q X. Micro- and macro-reaction kinetics study of ethylene epoxidation to ethylene oxide [D]. Beijing: Beijing University of Chemical Technology, 2022. |
| [11] |
BOSKOVIC G, DROPKA N, WOLF D, et al. Deactivation kinetics of Ag/Al2O3 catalyst for ethylene epoxidation[J]. Journal of Catalysis, 2004, 226(2): 334-342. DOI:10.1016/j.jcat.2004.06.003 |
| [12] |
凌泽济. 乙烯氧化反应器数学模拟[J]. 现代化工, 2011, 31(增刊1): 409-411. LING Z J. Mathematical simulation of ethylene oxidate reactor[J]. Modern Chemical Industry, 2011, 31(Suppl.1): 409-411. |
| [13] |
PESCHEL A, KARST F, FREUND H, et al. Analysis and optimal design of an ethylene oxide reactor[J]. Chemical Engineering Science, 2011, 66(24): 6453-6469. |
| [14] |
刘宗语, 谷彦丽. 乙烯环氧化反应器拟均相二维数学模型[J]. 石化技术, 2013, 20(1): 13-18. LIU Z Y, GU Y L. 2-D Pseudo-homogeneous mathematical model of ethylene epoxidation reactor[J]. Petrochemical Industry Technology, 2013, 20(1): 13-18. |
| [15] |
NAWAZ Z. Heterogeneous reactor modeling of an industrial multitubular packed-bed ethylene oxide reactor[J]. Chemical Engineering & Technology, 2016, 39(10): 1845-1857. |
| [16] |
顾芷玉. 列管式乙烯环氧化反应器性能分析与优化[D]. 北京: 北京化工大学, 2018. GU Z Y. Performance analysis and optimization of epoxidation of ethylene in a tubular fixed bed reactor [D]. Beijing: Beijing University of Chemical Technology, 2018. |
| [17] |
DIXON A G. Local transport and reaction rates in a fixed bed reactor tube: Exothermic partial oxidation of ethylene[J]. Chemical Engineering Science, 2021, 231: 116305. |
| [18] |
GALAN O, GOMES V G, ROMAGNOLI J, et al. Selective oxidation of ethylene in an industrial packed-bed reactor: Modelling, analysis and optimization[J]. International Journal of Chemical Reactor Engineering, 2009, 7(1): A32. |
| [19] |
ARYANA S, AHMADI M, GOMES V G, et al. Modelling and optimisation of an industrial ethylene oxide reactor[J]. Chemical Product and Process Modeling, 2009, 4(1): A14. |
| [20] |
XIE M Q, FREUND H. Optimal reactor design and operation taking catalyst deactivation into account[J]. Chemical Engineering Science, 2018, 175: 405-415. |
| [21] |
DELAVAR H, NADERIFAR A. Optimization of ethylene dichloride (EDC) and ethane concentrations to maximize catalytic ethylene oxide production rate and yield: Experimental study and modeling[J]. Chemical Engineering Science, 2022, 259: 117803. |
| [22] |
CHOWDHURY S, LAHIRI S K, HENS A, et al. Performance enhancement of commercial ethylene oxide reactor by artificial intelligence approach[J]. International Journal of Chemical Reactor Engineering, 2022, 20(2): 237-250. |
| [23] |
LAHIRI S K, KHALFE N. Process modeling and optimization of industrial ethylene oxide reactor by integratingsupport vector regression and genetic algorithm[J]. The Canadian Journal of Chemical Engineering, 2009, 87(1): 118-128. |
| [24] |
LUO N, DU W L, YE Z C, et al. Development of a hybrid model for industrial ethylene oxide reactor[J]. Industrial & Engineering Chemistry Research, 2012, 51(19): 6926-6932. |
| [25] |
韩晓霞. 混沌与支持向量机结合的多相催化建模与优化研究[D]. 太原: 太原理工大学, 2010. HAN X X. Study on modeling and optimization for heterogeneous catalysis based on chaos and support vector regression [D]. Taiyuan: Taiyuan University of Technology, 2010. |
| [26] |
包力, 高崇, 王树清, 等. 乙烯氧化制环氧乙烷合成反应器的模拟计算[J]. 化工科技, 1998, 6(3): 40-44. BAO L, GAO C, WANG S Q, et al. The simulation for reactor of ethylene oxidation to ethylene oxide[J]. Science & Technology in Chemical Industry, 1998, 6(3): 40-44. |
| [27] |
阿里云. 智能制造平台-AICS-产品简介[EB/OL]. (2021-04-21)[2022-12-20]. https://help.aliyun.com/document_detail/213072.html. ALI C. Artificial intelligence control system-AICS-Product introduction [EB/OL]. (2021-04-21)[2022-12-20]. https://help.aliyun.com/document_detail/213072.html. |
| [28] |
周志华. 机器学习[M]. 北京: 清华大学出版社, 2016: 133-139. ZHOU Z H. Machine learning[M]. Beijing: Tsinghua University Press, 2016: 133-139. |




