2. 华东理工大学 化学与分子工程学院,上海 200237
2. School of Chemistry and Molecular Engineering, East China University of Science and Technology, Shanghai 200237, China
近年随着尾气排放量和化石燃料燃烧量的增加,大气污染日趋严重。其中NO2是主要的污染物之一,是形成大气气溶胶、酸雨和对流层臭氧的主要因素[1],对人体健康和环境有很大的危害性,例如20 µg·g-1的NO2就可以对人体造成伤害[2]。过去的几十年中,我国NO2排放量的增长幅度在所有污染气中是最快的[3]。因此治理NO2的污染是一个紧迫的问题。其中一个有效的方法就是在NO2排放过程中通过吸附脱附将其回收利用。所以探索性研究NO2在吸附材料中的物理化学性能是十分必要的。
本研究主要探讨了NO2在MOFs材料中的扩散性能。MOFs作为一种新型纳米多孔材料,具有高孔隙率、低密度以及孔道可调性能,在气体储存、分离、催化和分子传感等领域具有广阔的应用前景[4]。国内外学者对气体分子在MOFs、沸石等材料中的吸附和分离性能进行了研究,但对于气体分子的动力学扩散过程研究较少,特别是NO2气体,中高继贤等[5]模拟研究了烟气中不同体积分数的SO2在ZL50活性炭中的扩散过程,结果表明SO2的有效内扩散系数随着SO2体积分数、吸附时间的增加不断增大。王鹏等[6]利用Fick扩散模型进行了CH4/N2在炭分子筛上的吸附动力学模拟,研究发现N2的扩散速率大于CH4的扩散速率。吴迪等[7]模拟研究了CH4在纳米多孔碳材料中的扩散行为,研究发现密度越小自扩散系数越大,且羧基修饰后自扩散系数最大。Liu等[8]模拟研究了氢气在10种IRMOF材料中的扩散速率,发现氢气在材料中的扩散系数与材料的自由体积成正比。Zhang等[9]模拟研究了纯CO2、CH4气体和混合气体在ZIF-8材料中的吸附和扩散,结果表明CO2的扩散性能受CH4影响很小,但是CH4的扩散系数随CO2浓度增大而减小。Yang等[10]模拟研究了甲醇、甘油和混合气体在IRMOF-1材料中的吸附和扩散,研究发现当甲醇的浓度增加时甘油的自扩散系数增加,协同促进效应增强。在分子水平上研究气体分子在MOFs材料中的扩散行为与其结构关系,不仅可为MOFs材料在气体吸附、分离等方面提供理论依据,还可为MOFs材料的分子设计和工艺开发提供科学技术指导。本研究通过分子动力学(MD)模拟研究NO2气体在多种MOFs材料中的分子动力学扩散过程,重点讨论自扩散系数与不同MOFs材料构效关系,并揭示NO2气体在MOFs材料中的扩散机理。
2 模拟方法根据前期吸附模拟工作结果,本文选择18种对NO2吸附性能好的MOFs材料作为本次研究对象,重点考察NO2在这些材料中的扩散性能。吸附性能好的MOFs材料筛选标准是常温常压下吸附容量大[11]。所选MOFs材料分别为Cd3BTB2、IRMOF-4、IRMOF-9、IRMOF-11、IRMOF-13[12]、MgMOF-74[13]、Mg-DOBDC、MIL-140B、MIL-47[14]、MIL-53Crht[15]、MIL-88A-dry、ZIF-2[16]、ZIF-3、ZIF-69[17]、ZIF-9、ZnBDC、ZnMOF-74和Zn-DOBDC[18]。由前期吸附模拟结果可知DREIDING力场参数[19]和UFF力场参数[20]可以很好模拟刚性MOFs材料物理化学性能,其具体力场参数见表 1。NO2的力场参数采用刚性分子模型,其具体力场参数和分子几何结构见表 2[21]。本研究中分子间的相互作用能U由Lennard-Jones势能和静电作用势能组成[22],公式如下:
|
|
表 1 MOFs材料的Lennard-Jones势能参数 Table 1 Lennard-Jones potential parameters of MOFs |
|
|
表 2 NO2的Lennard-Jones势能参数和分子几何构型 Table 2 Lennard-Jones potential parameters and geometry of NO2 |
| $U = \sum 4 {\varepsilon _{ij}}\left[ {{{\left( {\frac{{{\sigma _{ij}}}}{{{r_{ij}}}}} \right)}^{12}} - {{\left( {\frac{{{\sigma _{ij}}}}{{{r_{ij}}}}} \right)}^6}} \right] + \sum {\frac{{{q_i}{q_j}}}{{4\pi {\varepsilon _{\rm{0}}}{r_{ij}}}}} $ | (1) |
其中,εij和σij是LJ阱深和LJ直径,rij是i原子和j原子的距离,qi是i原子的电荷,ε0是真空介电常数。不同原子间Lennard-Jones势能参数由Lorentz-Berthelot混合规则[22]给出。
本研究采用MD模拟计算NO2分子随浓度变化在MOFs材料中的扩散系数。MD模拟均使用GROMACS软件包[23]在温度为298 K下正则系综(canonical ensemble,NVT)计算所得。其中模拟盒子采用MOFs材料的晶体参数构建,并在周期性边界条件下运用跳蛙(leap-frog)算法求解运动方程,温度采用Nosé-Hoover方法控制[22]。每个系统的模拟时间至少为10 ns,每一步积分步长为1 fs,其中前8 ns作为平衡时间,后2 ns为统计平均计算。Lennard-Jones势能采用Switch方法计算[22],其截断半径为1.1 nm。静电势能采用particle-mesh-ewald (PME)方法计算[24],其截断半径为1.1 nm。NO2采用刚性分子模型,其几何构型采用线性限制算法(LINCS)方法控制[25]。MOFs材料的原子固定不动,作为静止的原子固定在晶格参数位点上。自扩散系数Ds使用爱因斯坦关系式[10]由均方位移计算如下:
| $ {D_{\rm{s}}} = \mathop {\lim }\limits_{t \to \infty } \frac{1}{{6t}}\left[ {\frac{1}{N}{{\sum\limits_{k = 1}^N {\left| {{r_k}\left( t \right) - {r_k}\left( 0 \right)} \right|} }^2}} \right] $ | (2) |
其中,rk(0)和rk(t)分别为第k 个分子在初始时刻0和t时刻的位置,N为分子的总数。其中计算NO2气体随浓度变化的自扩散系数时气体分子间相互作用是打开。当计算无限稀释条件下NO2自扩散系数时气体分子间的相互作用关闭。
无限稀释条件下NO2自扩散系数是随温度变化的函数,其数值和活化能相关。本研究在温度从350到600 K的变化范围内模拟不同温度下的无限稀释自扩散系数D(0),并利用阿伦尼乌斯关系式[26]计算得到NO2气体在MOFs材料中的活化能Ea:
| $ D\left( 0 \right) = {D_{\rm{f}}}\exp \left( {\frac{{ - {E_{\rm{a}}}}}{{RT}}} \right) $ | (3) |
其中Df是指前因子,R是理想气体常数。
3 结果与讨论 3.1 NO2气体在MOFs材料扩散性能根据MOFs材料的结构特点分类比较NO2扩散性能。图 1是在18种MOFs材料中NO2气体自扩散系数随浓度变化曲线。其中MOFs材料的几何性质利用Zeo++程序计算获得[27],如表 3所示,依据MOFs材料的VF(孔隙率,void fraction)从大到小排列。
|
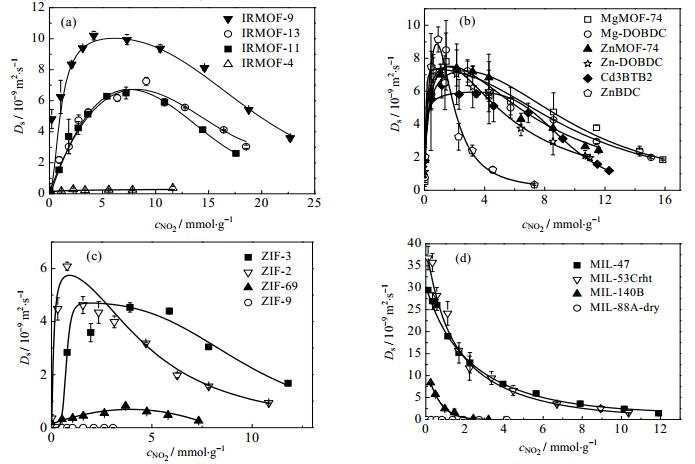
图 1 温度298 K时NO2在MOFs材料中自扩散系数曲线 Fig.1 Self-diffusivities of NO2 in MOFs at 298 K |
|
|
表 3 MOFs的几何结构性能 Table 3 Geometrical properties of MOFs |
图 1(a)是IRMOF (iso-reticular metal-organic frameworks)系列的MOFs材料,其中IRMOF-9,IRMOF-11和IRMOF-13是互穿结构。从图 1(a)可知在这三种材料中NO2气体的自扩散系数随着气体浓度增加先升高后降低。在NO2气体浓度为0.01~7.5 mmol·g-1时,因为MOFs材料表面吸附位点作用,NO2气体被束缚在材料孔道内表面。随着气体浓度的增加分子协同效应加剧,NO2气体受MOFs材料束缚减弱,因此自扩散系数随着浓度增大而升高。当NO2气体浓度大于7.5 mmol·g-1时,NO2气体的空间位阻效应增加,此时分子自扩散速率随着吸附浓度的增大逐渐减小。其中NO2在IRMOF-9中的自扩散系数相比其它三个材料要大,其最大自扩散系数可达10.2×10-9 m2·s-1。因为在这四种材料中IRMOF-9具有最大的SASA(可及表面积,accessible surface area)为3778 m2·g-1、VF为0.39和PLD(最小孔径,pore limiting diameter)为0.86 nm。IRMOF-13和IRMOF-11具有相同的几何结构性质,因此自扩散曲线保持一致。而IRMOF-4由于其SASA和VF相对最小,且PLD仅仅0.34 nm,所以NO2气体在其中处于束缚状态,其自扩散系数在(0.1~0.4)×10-9 m2·s-1区间之中。
图 1(b)是具有开放金属位点的MOFs材料,其中XMOF-74和X-DOBDC (X = Mg,Zn)框架结构类似,仅仅晶胞三边长度有所差异。其扩散性能也随着NO2气体的浓度增加先升高后降低。这四种材料的孔道都是规整的六边形结构,有机连结体都是苯环,金属簇结构一样,因此VF和孔径性质相似。所以NO2气体在这四种材料中的扩散速度主要由开放金属位点决定。从图 1(b)可知,在这四种材料中NO2气体浓度大于2 mmol·g-1时的自扩散系数范围大约在(2~7.6)×10-9 m2·s-1。其中NO2气体在ZnMOF-74和Zn-DOBDC材料中的扩散速率稍小,表明Zn金属对NO2气体的束缚较大。而另外两种具有开放金属位点的材料Cd3BTB2和ZnBDC表现出不同于以上4种材料的扩散性能,其主要原因是其框架几何结构不同。其中NO2气体在ZnBDC中表现为自扩散系数快速上升和快速下降趋势,其主要原因是VF较小,空间位阻效应随浓度增加快速显现出来。
图 1(c)是ZIF (zeolitic imidazolate frameworks)系列的MOFs材料,同样可知NO2气体在材料中的自扩散系数随着气体浓度增加先升高后降低。在这四种材料中NO2气体浓度大于1 mmol·g-1时自扩散系数范围大约在(0.2~6)×10-9 m2·s-1。其中NO2在ZIF-3中的自扩散系数最大,主要是因为ZIF-3具有最大的SASA为2897 m2·g-1、VF为0.21和PLD为0.57 nm。然而ZIF-9具有最小的SASA和VF,且PLD仅仅0.25 nm。又因为NO2分子的动态直径为0.401~0.512 nm[28],所以NO2气体在ZIF-9中束缚不动。由此可知NO2气体在此类材料中的扩散受PLD大小束缚,且扩散速率随着VF的增大而升高。
图 1(d)是MIL (materials institute lavoisier)系列的MOFs材料。模拟结果表明NO2气体在MIL系列材料中的自扩散系数随着气体浓度增加而降低,其中,在MIL-47和MIL-53Crht两种材料中NO2气体的扩散能力基本一致。两种材料的几何结构参数SASA、VF、PLD和LCD都比较相近,且都是通过苯环结构的连接体相连,仅仅是配位中心的金属元素分别是V和Cr。从扩散性能可以发现,金属配位中心和苯环连接体对NO2气体的束缚能力很差,使得NO2能够自由地在MIL-47和MIL-53Crht材料中的一维孔道中扩散。随着NO2气体浓度的升高,空间位阻效应增大,扩散速度随之减慢。在本研究的所有材料中,NO2气体在MIL-47和MIL-53Crht两种材料中扩散性能最佳,其最大值均大于30×10-9 m2·s-1。NO2气体在MIL-140B材料中自扩散系数趋势和以上两个材料一致,但是由于MIL-140B的VF下降到0.05,且最小孔径PLD为0.40 nm,因此扩散速率明显降低。当NO2气体在MIL-88A-dry材料中的时候,因为其最小孔径PLD仅为0.24 nm,小于NO2分子的动态直径为0.401~0.512 nm。因此NO2气体在MIL-88A-dry中束缚不动。
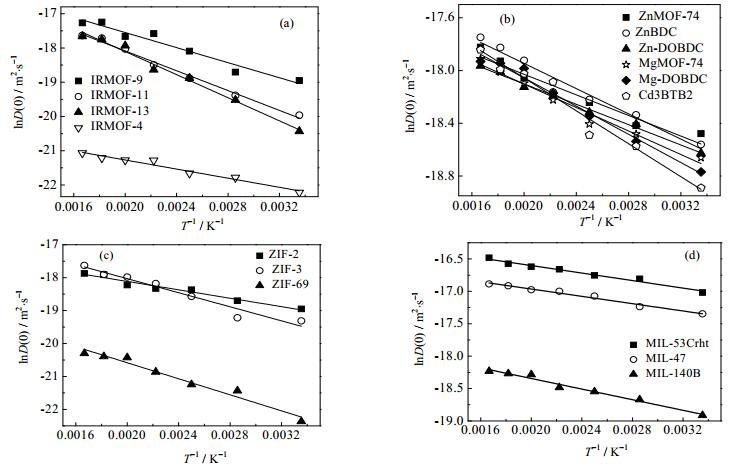
研究还考察了NO2在这18种MOFs材料中的无限稀释自扩散系数D(0)随温度的变化,并通过阿伦尼乌斯关系式(式(3))计算得到Df和Ea的数值,结果如表 4所示。无限稀释自扩散系数与温度关系如图 2所示,分别给出了以上4类MOFs材料的变化趋势。
|
|
表 4 NO2在MOFs材料中活化能和指前因子 Table 4 Activation energies and pre-factors of NO2 in MOFs |
|
图 2 无限稀释自扩散系数与温度关系图 Fig.2 Relationship between self-diffusivity at infinite dilution and temperature |
NO2气体在MOFs材料中随气体浓度的变化表现出了不同的扩散性能。通过对模拟轨迹的分析,得到NO2气体在不同的MOFs材料中的原子间距离随时间变化谱图和径向分布函数图(RDF),从而揭示其扩散机理。选取了两种不同的MOFs材料作为分析对象,分别是IRMOF-9和MIL-53Crht两种材料。NO2气体在其中表现出不同的自扩散性能,在IRMOF-9材料中自扩散系数随着气体浓度增加先升高后降低,而在MIL-53Crht材料中NO2气体自扩散系数随浓度增大而降低。
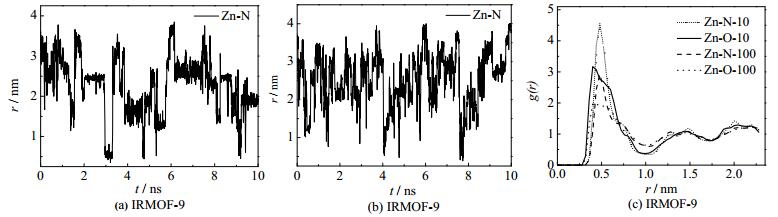
通过观察低浓度时的MD模拟轨迹发现,在IRMOF-9材料中NO2气体(10个NO2气体分子在3×2×2的IRMOF-9超晶胞里面,0.21 mmol·g-1)会长时间束缚在材料的吸附位点附近振动。分析此时NO2的N原子与IRMOF-9的Zn原子的距离随时间变化谱图如图 3(a),可以发现谱图振荡的频率较低,在多数时间段里Zn-N的相对距离保持恒定,自扩散系数为4.82×10-9 m2·s-1。表明低浓度的NO2气体在IRMOF-9中扩散时会束缚在不同的吸附位点,摆脱后又立即被另一吸附位点束缚住。随着NO2气体浓度的增加协同效应显著,如图 3(b)高浓度NO2气体在IRMOF-9材料(100个NO2气体分子在3×2×2的IRMOF-9超晶胞里面,2.1 mmol·g-1)中Zn-N距离随时间变化谱图。此时谱图振荡的频率增强,NO2气体在IRMOF-9材料中扩散时束缚明显缩短,自扩散系数增大为8.34×10-9 m2·s-1。分析NO2气体与IRMOF-9材料中Zn原子的RDF曲线可以得出相同的结论。如图 3(c)所示,低浓度的NO2气体在IRMOF-9材料的RDF曲线为Zn-N-10短点线和Zn-O-10实线。此时RDF曲线震荡幅度较大,表现为固相的曲线特征,NO2气体原子相对Zn原子分布处于相对固定的位置,说明NO2气体的自扩散速率较慢。高浓度的NO2气体在IRMOF-9材料的RDF曲线为Zn-N-100虚线和Zn-O-100点线。此时RDF曲线震荡幅度明显减弱,表现为气相的曲线特征,说明NO2气体的自扩散速率变快。
|
图 3 NO2气体在IRMOF-9中的原子间距离随时间变化谱图(a,b)和径向分布函数图(c) Fig.3 Atom distance as a function of time (a, b) for NO2 in IRMOF-9 and RDF (c) |
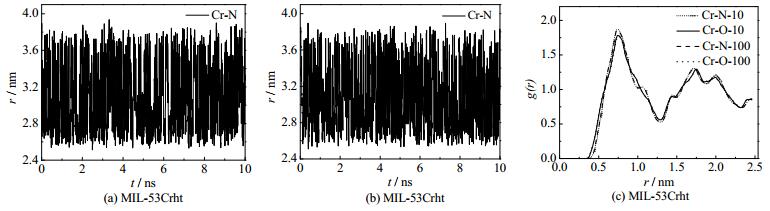
NO2气体在MIL-53Crht材料表现出不同的扩散性能。从图 4(a)、(b)不同浓度NO2气体在MIL-53Crht材料(10个和100个NO2气体分子在3×4×8的MIL-53Crht超晶胞里面,浓度分别为0.11和1.1 mmol·g-1)中Cr-N距离随时间变化谱图的振荡频率基本相同,说明在任何浓度下,NO2气体在MIL-53Crht中的自扩散性能,不受其吸附位点的约束。通过模拟轨迹的观察同样可知,此时NO2气体在MIL-53Crht中无论浓度高低都在自由运动。同时由图 4(c)的RDF曲线可知,在高低浓度时Cr-N-10短点线和Cr-N-100虚线,以及Cr-O-10实线和Cr-O-100点线基本重合,说明NO2气体不受附位点束缚表现为相同的气相流动性质。因此NO2气体在MIL-53Crht材料的自扩散系数主要受空间位阻效应影响,随浓度增大而降低。
|
图 4 NO2气体在MIL-53Crht中的原子间距离随时间变化谱图(a,b)和径向分布函数图(c) Fig.4 Atom distance as a function of time (a, b) for NO2 in MIL-53Crht and RDF (c) |
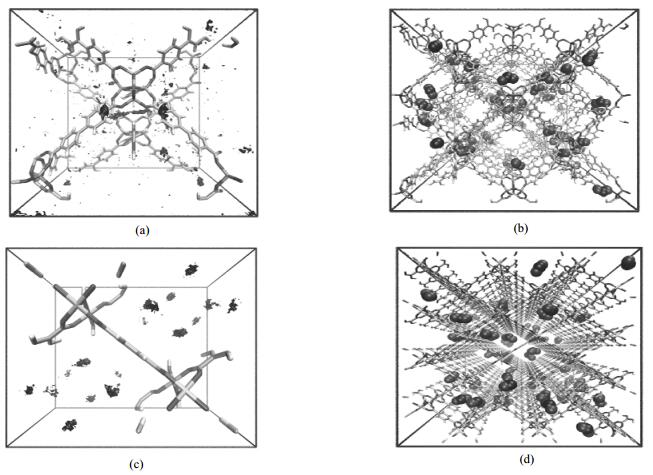
图 5表示NO2在IRMOF-9和MIL-53Crht材料的吸附密度图和MD模拟截图。通过前期的MC模拟结果分析可得吸附密度图,图 5(a),(c)表示NO2在IRMOF-9和MIL-53Crht单晶胞中的高吸附位点(黑色密度云),吸附密度云越大表明该位置吸附NO2气体几率越高。由图 5(a)可知,IRMOF-9材料吸附NO2气体的吸附位点主要在Zn金属簇周围,MD模拟截图图 5(b)同样证明NO2气体束缚位点就是IRMOF-9材料高吸附位点。由图 5(c)可知,MIL-53Crht材料吸附NO2气体的吸附位点主要在一维孔道中心靠近苯环的平面,且吸附密度云的大小分散平均。此时表明Cr金属簇对NO2气体吸附能力较弱,因此NO2气体受高吸附位点影响较小。从MD模拟截图图 5(d)可见,NO2气体在孔道中心自由移动,并没有停留在某一个吸附位点附近。通过以上分析表明,当MOFs材料存在强金属簇吸附位点的时候,NO2气体受到吸附位点影响,先表现出协同促进效应自扩散速率随浓度增加而增大,后表现为空间位阻效应自扩散速率随浓度增加而减小。如果MOFs材料没有强吸附位点的时候,NO2气体不受到吸附位点影响,仅仅表现为空间位阻效应自扩散速率随浓度增加而减小。
|
图 5 NO2在IRMOF-9和MIL-53Crht材料吸附密度图(a,c)和MD模拟截图(b,d) Fig.5 Adsorption density diagrams (a, c) and snapshot of MD simulation (b, d) for NO2 in IRMOF-9 and MIL-53Crht |
本研究利用MD模拟研究了NO2气体在18种MOFs材料中随浓度增加的自扩散性能,并分析了NO2气体在MOFs材料中的扩散机理。通过对自扩散系数的结果分析,NO2气体在IRMOF系列材料、具有开放金属位点的MOFs材料和ZIF系列材料中的自扩散系数随着气体浓度增加先升高后降低;然而在MIL系列材料中自扩散系数仅随着气体浓度增加而降低。同时研究表明在IRMOF-9、MgMOF-74、ZiF-3、MIL-47和MIL-53Crht等材料中NO2气体均具有较好扩散性能。其主要受材料PLD和VF影响,在同系列材料中PLD和VF越大NO2气体的自扩散系数越大。因此对MOFs材料几何结构的合理设计,决定NO2气体自扩散性能。
研究扩散机理发现,MOFs材料金属簇吸附性能的强弱影响NO2气体随浓度变化的自扩散系数曲线。当有强金属簇吸附位点的时候,NO2气体自扩散性能先受到协同促进效应影响,后受到空间位阻效应影响;当无强金属簇吸附位点的时候,主要受空间位阻效应影响。
| [1] | Frost G J, McKeen S A, Trainer M, et al. Effects of changing power plant NOx emissions on ozone in the eastern United States:proof of concept[J]. Journal of Geophysical Research, 2006, 111: D12306. DOI:10.1029/2005JD006354. |
| [2] | Barea E, Montoro C, Navarro J A. Toxic gas removal-metal-organic frameworks for the capture and degradation of toxic gases and vapours[J]. Chemical Society Reviews, 2014, 43(16): 5419-5430. DOI:10.1039/C3CS60475F. |
| [3] | Zhang Q, Geng G, Wang S, et al. Satellite remote sensing of changes in NOx emissions over China during 1996-2010[J]. Chinese Science Bulletin, 2012, 57(22): 2857-2864. DOI:10.1007/s11434-012-5015-4. |
| [4] | Snurr R Q, Hupp J T, Nguyen S T. Prospects for nanoporous metal-organic materials in advanced separations processes[J]. AIChE Journal, 2004, 50(6): 1090-1095. DOI:10.1002/(ISSN)1547-5905. |
| [5] | GAO Ji-xian(高继贤), WANG Tie-feng(王铁峰), SHU Qing(舒庆), et al. Intraparticle diffusion mechanism and kinetic models of adsorptive flue gas desulphurization by ZL50 activated carbon(ZL50活性炭吸附烟气脱硫过程的内扩散机制及其动力学模型)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报), 2010, 24(3): 402-409. DOI:10.3969/j.issn.1003-9015.2010.03.007. |
| [6] | WANG Peng(王鹏), SHI Yao-qi(石耀琦), MA Zheng-fei(马正飞), et al. Study on adsorption equilibrium and diffusion model of CH4 and N2 on a carbon molecular sieve(CH4/N2在炭分子筛上的吸附平衡与扩散模型)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报), 2014, 28(3): 484-488. |
| [7] | WU Di(吴迪), WANG Shan-shan(王珊珊), LÜ Ling-hong(吕玲红), et al. CH4 storage in nanoporous activated carbon by molecular simulation(孔活性炭储存CH4的分子模拟)[J]. CIESC Journal(化工学报), 2016, 67(9): 3707-3719. |
| [8] | Liu B, Yang Q, Xue C, et al. Molecular simulation of hydrogen diffusion in interpenetrated metal-organic frameworks[J]. Physical Chemistry Chemical Physics, 2008, 10(22): 3244-3249. DOI:10.1039/b801494a. |
| [9] | Zhang L L, Wu G, Jiang J W. Adsorption and diffusion of CO2 and CH4 in zeolitic imidazolate framework-8:effect of structural flexibility[J]. Journal of Physical Chemistry C, 2014, 118(17): 8788-8794. DOI:10.1021/jp500796e. |
| [10] | Yang L, Sandler S I, Vlachos D G, et al. Adsorption and diffusion of methanol, glycerol, and their mixtures in a metal organic framework[J]. Industrial & Engineering Chemistry Research, 2011, 50(24): 14084-14089. |
| [11] | Zhou X, Su Z, Chen H, et al. Capture of pure toxic gases through porous materials from molecular simulations[J]. Molecular Physics, 2018. DOI:10.1080/00268976.2018.1440019. |
| [12] | Eddaoudi M, Kim J, Rosi N, et al. Systematic design of pore size and functionality in isoreticular MOFs and their application in methane storage[J]. Science, 2002, 295(5554): 469-472. DOI:10.1126/science.1067208. |
| [13] | Krishna R, van Baten J M. Investigating the potential of MgMOF-74 membranes for CO2 capture[J]. Journal of Membrane Science, 2011, 377(1): 249-260. |
| [14] | Barthelet K, Marrot J, Riou D, et al. A breathing hybrid organic-inorganic solid with very large pores and high magnetic characteristics[J]. Angewandte Chemie, International Edition, 2002, 41(2): 281-284. DOI:10.1002/1521-3773(20020118)41:2<281::AID-ANIE281>3.0.CO;2-Y. |
| [15] | Rosenbach N, Jobic H, Ghoufi A, et al. Diffusion of light hydrocarbons in the flexible MIL-53(Cr) metal-organic framework:a combination of quasi-elastic neutron scattering experiments and molecular dynamics simulations[J]. Journal of Physical Chemistry C, 2014, 118(26): 14471-14477. DOI:10.1021/jp504900q. |
| [16] | Park K S, Ni Z, Cote A P, et al. Exceptional chemical and thermal stability of zeolitic imidazolate frameworks[J]. Proceedings of the National Academy of Sciences of the United States of America, 2006, 103(27): 10186-10191. DOI:10.1073/pnas.0602439103. |
| [17] | Banerjee R, Phan A, Wang B, et al. High-throughput synthesis of zeolitic imidazolate frameworks and application to CO2 capture[J]. Science, 2008, 319(5865): 939-943. DOI:10.1126/science.1152516. |
| [18] | Liu J, Benin A I, Furtado A M, et al. Stability effects on CO2 adsorption for the DOBDC series of metal-organic frameworks[J]. Langmuir, 2011, 27(18): 11451-11456. DOI:10.1021/la201774x. |
| [19] | Bae Y S, Yazaydin A O, Snurr R Q. Evaluation of the BET method for determining surface areas of MOFs and zeolites that contain ultra-micropores[J]. Langmuir, 2010, 26(8): 5475-5483. DOI:10.1021/la100449z. |
| [20] | Rappe A K, Casewit C J, Colwell K S, et al. UFF, a full periodic table force field for molecular mechanics and molecular dynamics simulations[J]. Journal of the American Chemical Society, 1992, 114(25): 10024-10035. DOI:10.1021/ja00051a040. |
| [21] | Sun W Z, Lin L C, Peng X, et al. Computational screening of porous metal-organic frameworks and zeolites for the removal of SO2 and NOx from flue gases[J]. AIChE Journal, 2014, 60(6): 2314-2323. DOI:10.1002/aic.14467. |
| [22] | Frenkel D, Smit B. Understanding molecular simulation:from algorithms to applications[M].San Diego: Academic Press, 2002. |
| [23] | Lindorff-Larsen K, Piana S, Palmo K, et al. Improved side-chain torsion potentials for the Amber ff99SB protein force field[J]. Proteins, 2010, 78(8): 1950-1958. |
| [24] | Darden T, York D, Pedersen L. Particle mesh Ewald:an N·log(N) method for E wald sums in large systems[J]. The Journal of Chemical Physics, 1993, 98(12): 10089-10092. DOI:10.1063/1.464397. |
| [25] | Hess B, Bekker H, Berendsen H J C, et al. LINCS:a linear constraint solver for molecular simulations[J]. Journal of Computational Chemistry, 1997, 18(12): 1463-1472. DOI:10.1002/(ISSN)1096-987X. |
| [26] | Babarao R, Jiang J. Diffusion and separation of CO2 and CH4 in silicalite, C168 schwarzite, and IRMOF-1:a comparative study from molecular dynamics simulation[J]. Langmuir, 2008, 24(10): 5474-5484. DOI:10.1021/la703434s. |
| [27] | Martin R L, Smit B, Haranczyk M. Addressing challenges of identifying geometrically diverse sets of crystalline porous materials[J]. Journal of Chemical Information and Modeling, 2012, 52(2): 308-318. DOI:10.1021/ci200386x. |
| [28] | Bobbitt N S, Mendonca M L, Howarth A J, et al. Metal-organic frameworks for the removal of toxic industrial chemicals and chemical warfare agents[J]. Chemical Society Reviews, 2017, 46(11): 3357-3385. DOI:10.1039/C7CS00108H. |




