2. 中国矿业大学 深部岩土力学与地下工程国家重点实验室, 江苏 徐州 221116;
3. 中国矿业大学 国际学院, 江苏 徐州 221116
2. State Key Laboratory for GeoMechanics and Deep Underground Engineering, Xuzhou 221116, China;
3. International College, China University of Mining and Technology, Xuzhou 221116, China
超声波辅助冷却冻结在食品冻结保鲜[1]、医用治疗[2]、生物化学[3-4]等领域得到广泛的应用,具有较好的应用前景。如何利用超声波实现高效冻结成为近年来广泛关注的问题之一。Wang等[5]通过基于熵方法的纯物质冻结相场模型追踪冻结过程中固-液交界面的位置移动。赵凯璇等[6]建立了真空环境中单液滴闪蒸冻结模型,分析了环境压力和温度对于液滴温度和半径变化的影响。耿县如等[7]讨论了液滴大小、气体流速、环境温度对液滴温度和凝固时间的影响。吕明等[8]结合Rayleigh-Plesset方程对液滴内空化气泡生长机理和过程进行了模拟分析。Virone等[9]设计了一种超声波空穴反应器,给出了空化效应所产生气泡的膨胀、破裂方程以及溶液结核速度的计算公式,分析了溶液温度和结核速度的变化规律。Mathieu等[10]研究了在超声波作用下水冻结产生的冰核数量与液体温度和超声波压力间的关系,建立了超声波空化作用下单个气泡的Navier-Stokes equations方程(简称N-S方程),获得了实际液滴空化效应产生的冰核数。余德洋[11]利用显微成像技术分析了纯水、蔗糖溶液在超声波作用下的结晶以及超声波对冰晶二次成核和冰晶生长速度的影响。
已有文献探讨了超声波强化冻结成核和冰晶的生长机理,但对于超声波作用下冻结过程中热质传递机理研究较少,尚未阐明超声波空化效应和热效应在冷却冻结过程中的作用机理。本文将在声场理论的基础上,结合液滴冷却冻结热质传递规律,建立超声波作用下液滴冻结的热质传递模型,研究超声波作用下液滴冻结过程中液滴温度、液固界面、直径大小的变化规律,确定超声波空化效应导致传质引起的热传递量与超声波热效应产热量的变化关系,为超声波辅助冻结的高效利用提供参考和指导。
2 液滴冷却冻结模型 2.1 物理模型及实验装置超声波分为2大类:一类为高频率、低能量诊断超声波;另一类为强化液体结晶的低频率、高能量超声波[12]。超声波空化效应[13]是液体中微气泡在声场作用下快速膨胀、闭合、崩溃,强化了液滴表面与周围环境间的传质,有助于降低界面能[14]和提高液滴的成核速度[15]。超声波作用下液滴冻结模型如图 1所示。
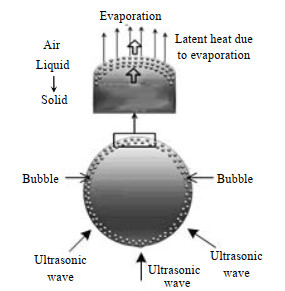
|
图 1 超声波作用下液滴冷却冻结示意图 Fig.1 Schematic diagram of droplet cooling and freezing under ultrasonic |
超声波作用下液滴冻结实验装置见图 2,将液滴悬挂于低温箱中,通过容器底部布置的超声波发生器输入超声波,利用显微镜对液滴冻结进行观测。实验中采用的设备为金相显微镜SGO-BH200M (物镜放大倍数为5~50倍)、高速摄像机(拍摄帧数15 000 fps)、热电偶(测量范围-40~150 ℃)、超声波发生器(超声波频率20~100 kHz,强度0~2 000 W·m-2)以及恒温恒湿箱(初始温度设置为-15 ℃),液滴的初始直径2.0 mm。
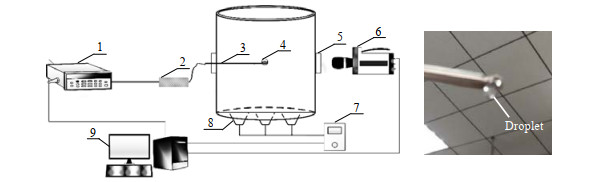
|
图 2 超声波作用下液滴冻结实验系统 Fig.2 Experiment setup of droplet freezing under ultrasonic 1.data collector 2.temperature transition 3.themocouple 4.droplet 5.observation window 6.high-speed camera 7.ultrasonic generator 8.ultrasonic vibrator 9.collection system |
对于相变冻结过程,Feuillebois等[16]、张跃凯[17]根据冻结条件的差异将冻结过程进行了不同的划分。结合超声波作用下液滴的实际冷却冻结过程,将液滴的冷却冻结分为2个阶段:1) 蒸发冷却过程,液滴蒸发冷却至凝固点,液滴表面状态从液态转变为固态;2) 液滴深度冻结过程,从表面向内部进行冻结,液滴由液固状态逐渐转变为固态。
液滴表面蒸发过程中的传质为
| $ \dot m = - 4{\rm{ \mathsf{ π}}} {R_{\rm{d}}}^2{D_{\rm{V}}}\frac{{{\rm{d}}{\rho _{{\rm{vapour}}}}}}{{{\rm{d}}{R_{\rm{d}}}}} $ | (1) |
将水蒸气视为理想气体,根据理想气体状态方程,由式(1)得
| $ \dot m = {\rm{ - }}4{\rm{ \mathsf{ π}}} {R_{\rm{d}}}{D_{\rm{v}}}\frac{M}{R}\left( {\frac{{{p_{\rm{d}}}}}{{{T_{\rm{d}}}}} - \frac{{{p_{\infty }}}}{{{T_\infty }}}} \right) = \frac{{{\rm{d}}(\frac{{\rm{ \mathsf{ π}}} }{6}\rho {D^3})}}{{{\rm{d}}t}} $ | (2) |
超声波作用下液滴在蒸发过程中的热量交换包括超声波热效应的产热量Qheat、液滴表面对流换热量Qconv、液滴表面传质引起的传热量Qevap、液滴内部的能量变化为Qin,其能量方程为
| $ {Q_{{\rm{in}}}} = {Q_{{\rm{conv}}}} + {Q_{{\rm{evap}}}} - {Q_{{\rm{heat}}}} $ | (3) |
液滴内部的能量变化:
| $ {Q_{{\rm{in}}}} = \frac{{\rm{ \mathsf{ π}}} }{6}\rho c{D^3}\Delta {T_{\rm{d}}} $ | (4) |
液滴表面对流换热量:
| $ {Q_{{\rm{conv}}}} = h{\rm{ \mathsf{ π}}} {D^2}\left( {{T_{\rm{d}}} - {T_\infty }} \right) $ | (5) |
式(5)中液滴与周围环境的对流传热系数[18]:
| $ h = \frac{{\left( {2 + 0.6 \cdot R{e^{1/2}} \cdot Pr{}^{1/3}} \right)\lambda }}{D} $ | (6) |
液滴表面传质引起的传热量:
| $ {Q_{{\rm{evap}}}} = {\rm{ \mathsf{ π}}} {D^2}{L_{{\rm{evap}}}}{H_{\rm{m}}}\frac{M}{R}\left( {\frac{{{p_{\rm{d}}}}}{{{T_{\rm{d}}}}} - \frac{{{p_{\infty }}}}{{{T_\infty }}}} \right) $ | (7) |
式(7)中液滴表面的对流传质系数[19]:
| $ {H_{\rm{m}}} = 2\sqrt {\frac{{{D_{{\rm{GLS}}}}f}}{\pi }} \phi + \left( {\frac{{\left( {2 + 0.6 \cdot S{c^{1/3}} \cdot R{e^{1/2}}} \right)}}{D} \cdot {D_{{\rm{GLS}}}}} \right) \times \left( {1 - \phi } \right) $ | (8) |
当液滴表面冻结成固体时,其表面与周围气流之间的有效扩散系数为
| $ {D_{{\rm{GS}}}} = \frac{{K({D_{\rm{v}}} + {D_{{\rm{GA}}}})}}{\tau } $ | (9) |
当液滴处于固液共存状态时,液滴中液体所占的比例为
| $ {D_{{\rm{GLS}}}} = \kappa {D_{\rm{v}}} + \left( {1 - \kappa } \right){D_{{\rm{GS}}}} $ | (10) |
超声波热效应产热量:
| $ {Q_{{\rm{heat}}}} = 2\beta I{V_{\rm{d}}} $ | (11) |
超声波作用在液滴上总的衰减系数由黏滞衰减系数αη、热传导衰减系数αξ和散射衰减系数αs组成,各部分的计算式如式(12)~(14):
| $ {\alpha _{\rm{ \mathsf{ η} }}} = \frac{{2{{\rm{ \mathsf{ π}}} ^2}{f^2}\eta }}{{{\rho _{\rm{d}}}{c^3}}} $ | (12) |
| $ {\alpha _\xi } = \frac{{2{{\rm{\pi }}^2}{f^2}{\lambda _{{\rm{liquid}}}}}}{{{\rho _{\rm{d}}}{c^3}}}\left( {\frac{1}{{{c_v}}} - \frac{1}{{{c_p}}}} \right) $ | (13) |
| $ {\alpha _{\rm{S}}} = \frac{8}{3}\frac{{{{\rm{ \mathsf{ π}}} ^4}{R_{\rm{d}}}^3{f^4}}}{{{c^4}}} $ | (14) |
考虑液滴孔隙率的影响,液滴对超声波总的吸收系数为[20]
| $ \beta = \left( {1 - K} \right)\left( {\frac{{2{{\rm{ \mathsf{ π}}} ^2}{f^2}\eta }}{{{\rho _{\rm{d}}}{c^3}}} + \frac{{2{{\rm{ \mathsf{ π}}} ^2}{f^2}\lambda {{\kern 1pt} _{{\rm{liquid}}}}}}{{{\rho _{\rm{d}}}{c^3}}}\left( {\frac{1}{{{c_V}}} - \frac{1}{{{c_p}}}} \right)} \right) + K\left( {\frac{8}{3}\frac{{{{\rm{ \mathsf{ π}}} ^4}{R_{\rm{d}}}^3{f^4}}}{{{c^4}}}} \right) $ | (15) |
根据能量守恒,能量变化量等于进入液滴的能量和离开液滴的能量的差值,由式(4)、(5)、(7)和(11)得到液滴冷却能量方程:
| $ \frac{{\rm{ \mathsf{ π}}} }{6}{\rho _{{\rm{liquid}}}}{c_p}_{{\rm{(liquid)}}}{D^3}\Delta {T_{\rm{d}}} = [h{\rm{ \mathsf{ π}}} {D^2}\left( {{T_{\rm{d}}} - {T_\infty }} \right) + {\rm{ \mathsf{ π}}} {D^2}{H_{\rm{m}}}{L_{{\rm{evap}}}}\frac{M}{R}\left( {\frac{{{p_{\rm{d}}}}}{{{T_{\rm{d}}}}} - \frac{{{p_\infty }}}{{{T_\infty }}}} \right) - 2\beta I{V_{\rm{d}}}] \cdot t $ | (16) |
对于液滴的深度冻结阶段,考虑液滴表面已全部由液态转变为固态。液滴的凝固释放潜热Qsolid,冻结过程应满足能量平衡关系式
| $ {Q_{{\rm{in}}}} = {Q_{{\rm{conv}}}} + {Q_{{\rm{evap}}}} - {Q_{{\rm{heat}}}} - {Q_{{\rm{solid}}}} $ | (17) |
液滴的凝固放热量Qsolid为
| $ {Q_{{\rm{solid}}}} = {\rho _{{\rm{solid}}}}{L_{{\rm{solid}}}}\frac{{{\rm{d}}{V_{\rm{d}}}}}{{{\rm{d}}t}} $ | (18) |
同理得到液滴冻结过程中能量方程:
| $ \frac{{\rm{ \mathsf{ π}}} }{6}{\rho _{{\rm{solid}}}}{c_{p\left( {{\rm{solid}}} \right)}}{D^3}\Delta {T_p} = [h{\rm{ \mathsf{ π}}} {D^2}\left( {{T_{\rm{d}}} - {T_\infty }} \right) + {\rm{ \mathsf{ π}}} {D^2}{H_{\rm{m}}}{L_{{\rm{evap}}}}\frac{M}{R}\left( {\frac{{{p_{\rm{d}}}}}{{{T_{\rm{d}}}}} - \frac{{{p_\infty }}}{{{T_\infty }}}} \right) - 2\beta I{V_{\rm{d}}} - {\rho _{{\rm{solid}}}}{L_{{\rm{solid}}}}\frac{{{\rm{d}}{V_{\rm{d}}}}}{{{\rm{d}}t}}] \cdot t $ | (19) |
利用超声波作用下液滴冷却冻结模型分析不同的初始液滴直径、超声波强度及频率下,液滴的直径、温度、固液交界面位置随时间的变化规律,探讨超声波热效应产热量和超声波作用下液滴表面传质引起传热量的变化规律,确定超声波作用时间对冻结的影响。模拟计算过程中主要参数见表 1。
|
|
表 1 主要参数 Table 1 Parameters for model simulation |
超声波和无超声波作用下液滴冷却冻结过程中直径的变化规律见图 3。超声波强化了液滴与周围环境的质传递,因此超声波作用下液滴直径随时间变化剧烈,减小速度较快。超声波声强周期性变化,导致液滴和环境之间的压力差会出现正负交替,从而使液滴直径出现一定的往复变化。当液滴进入凝固升华阶段时,水的体积会膨胀,所以液滴直径先增大后减小,最终趋于稳定。可见,超声波可有效强化液滴的冷却冻结,未加超声波时液滴的冻结最终直径为0.993 8 mm,液滴的直径减少了0.62%,加载超声波的液滴最终直径为0.977 3 mm,减少了2.27%。
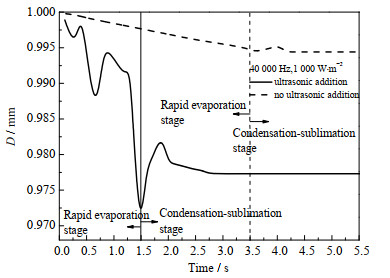
|
图 3 超声波作用和无超声波作用液滴冻结过程中直径随时间的变化规律 Fig.3 Profiles of droplet diameter in freezing processes with and without ultrasonic |
在不同的液滴初始直径2.0、1.6和1.0 mm下,液滴直径随冻结时间变化规律如图 4所示。从图 4可以看出,当液滴完全冻结时液滴直径分别减少0.12、0.04和0.022 7 mm。液滴初始直径越大,最终直径减少越多。原因在于液滴的初始直径越大,液滴与环境相接触的表面积越大,液滴表面传质越强。
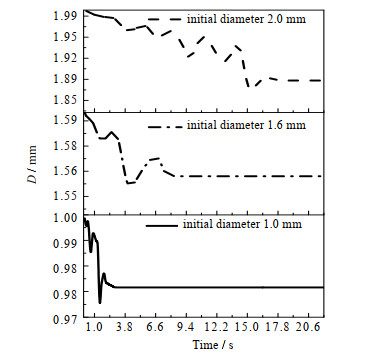
|
图 4 不同大小液滴直径随冻结时间的变化规律 Fig.4 Profiles of droplet diameter as a function of freezing time |
超声波和无超声波作用下液滴冷却冻结过程中温度变化规律见图 5。从图 5中可以看出在超声波作用下,液滴的温度下降较快(超声波作用下液滴的蒸发阶段时间比无超声波作用的时间缩短1/2左右)。冷却冻结相同时间,无超声波作用时液滴的最低温度可以达270.9 K;在超声波作用下液滴的最低温度可以达到264.9 K。因为超声波空化效应增强了液滴与周围环境间的传质,导致传质引起的传热量增加,从而促进了液滴的冷却冻结,这一结果与文献[21-22]的研究结论一致。
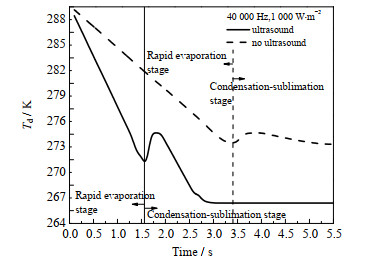
|
图 5 超声波作用和无超声作用波液滴冻结过程中温度随时间的变化规律 Fig.5 Profiles of droplet temperature in freezing processes with and without ultrasonic |
液滴冻结过程中液滴直径与液滴温度随时间的变化规律如图 6所示。分析过程中液滴过冷度设为5 K,在到达液滴凝固点前,液滴快速蒸发,温度不断降低,直径也逐渐减小。从图 6中可以看出液滴在冻结过程中温度变化与液滴直径的变化趋势基本一致,当液滴经过凝固点后,液滴膨胀直径增大,同时液滴凝固释放的热量会导致液滴的温度出现短暂上升随后下降。
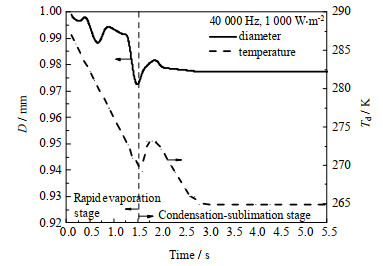
|
图 6 超声波作用下液滴冻结过程中液滴直径D和温度Td随时间的变化规律 Fig.6 Profiles of droplet diameter D and temperature Td in freezing processes with ultrasonic |
当超声波的频率为40 000 Hz,强度分别为1 000、700、400 W·m-2,液滴初始半径r=1.0 mm时,冻结过程中液固界面位置的变化见图 7。图 7表明超声波强度较大时液滴冷却冻结过程中热质传递较强,液固交界面的移动速度较快,液滴由外到内完全冻结所需要时间较短,曲线的斜率越大。当超声波强度分别为1 000、700和400 W·m-2时,液滴液固交界面移动到液滴中心的时间分别为46、48和54 s。
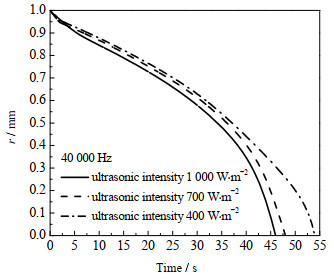
|
图 7 不同超声波强度下液滴冻结过程中液固交界面位置随时间的变化规律 Fig.7 Profiles of droplet solid-liquid interface position in freezing processes under different ultrasonic intensities |
不同大小液滴在冷却冻结过程中液固交界面位置随时间的变化规律见图 8,根据曲线的斜率可以得到液滴的固-液交界面位置随时间的变化速度。液滴的直径越小,其液固交界面的移动速度越快,液滴冻结所需的时间越短。因为在相同的超声波强度、频率和外界条件下,液滴的直径越小,液滴内部单位体积所产生气泡的数量越多,液滴表面与周围环境的传质过程越剧烈,使液滴冷却冻结得到强化。
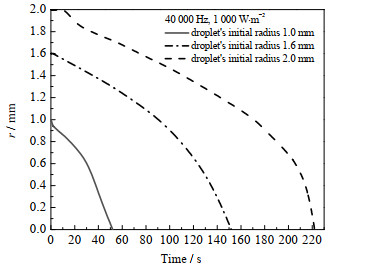
|
图 8 不同大小液滴冻结过程中液固交界面随时间的变化规律 Fig.8 Profiles of droplet solid-liquid interface position in freezing processes for different droplet radius |
超声波辅助冷却冻结过程中,超声波空化效应增强了液滴与周围环境之间的传质和传热,而超声波热效应会产生热量(相当于增加了内热源)。蒸发冻结前期,超声波空化效应导致传质引起的传热量较大,超声波有利于液滴的快速蒸发冻结。当液滴表面开始冻结,液态水所占比例下降,超声波空化效应导致传质引起的传热逐渐减弱,在液滴冻结的某个时刻,超声波热效应的产热量将大于超声波空化效应传质引起的传热量,此后加载超声波不能强化液滴的冷却冻结。
不同超声波频率下,超声波空化效应导致传质引起的传热量和超声波热效应产热量的变化规律见图 9。图中虚线表示不同超声波频率下超声波热效应产热量,实线表示超声波空化效应导致传质引起的传热量。在初始阶段,空化效应有助于液滴表面的传质,强化了液滴表面的传热。随着冻结的进行,液滴表面逐渐由液态转变为固态,液滴外表面的传质减弱,导致传质引起传热量增加的幅度逐渐减小,之后出现下降;而超声波热效应的产热量随时间逐渐增加。当到达临界点C1、C2、C3、C4、C5和C6即超声波热效应产热量与空化效应传质引起的传热量相等的位置时,超声波热效应的产热量与空化效应传质引起的传热量相等,此后加载超声波不能起到强化冷却冻结的效果。
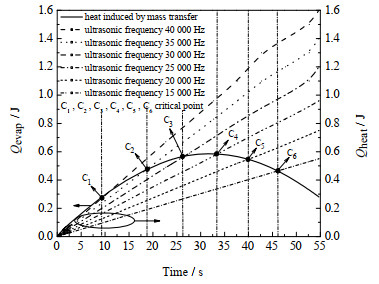
|
图 9 液滴在不同超声波频率下传质的传热量Qevap和超声波热效应产热量Qheat的变化规律 Fig.9 Profiles of heat by mass transfer Qevap and heat by ultrasonic thermal effect Qheat under different ultrasonic frequencies |
不同超声波强度下超声波空化效应导致传质引起的传热量和超声波热效应产热量的变化见图 10。图中虚线表示超声波热效应的产热量,实线表示超声波空化效应导致传质引起的传热量。液滴与周围环境间传质导致的传热量曲线与超声波热效应产热量曲线的交点(临界点)C1、C2、C3和C4,随着超声波强度的降低向后移动。同样临界点之后液滴内超声波热效应的产热量将大于超声波空化效应传质引起的传热量,此后加载超声波不利于液滴的冻结。
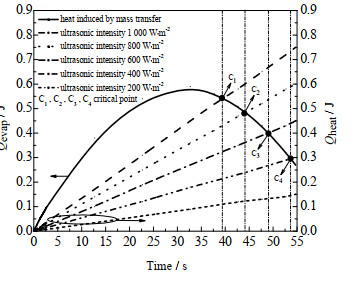
|
图 10 液滴在不同超声波强度下的传质传热量Qevap和超声波热效应产热量Qheat的变化规律 Fig.10 Profiles of heat by mass transfer Qevap and heat by ultrasonic thermal effect Qheat under different ultrasonic intensities |
在液滴冷却冻结实验的基础上,将超声波和无超声波作用下液滴冻结过程中固液界面的实验结果与模拟结果进行了对比,见图 11。实线表示超声波作用下液滴液固界面位置随时间变化的模拟曲线。实验中在-15 ℃的环境中,超声波作用下液滴完全冻结需要52 s,无超声波作用需要65 s,可以发现超声波作用下液滴更容易冻结。对比实验与模拟结果,两者最大误差10.6%,最小误差0.3%,且两者变化趋势相同,表明该理论模型能够较好地模拟预测超声波作用下液滴的冷却冻结。
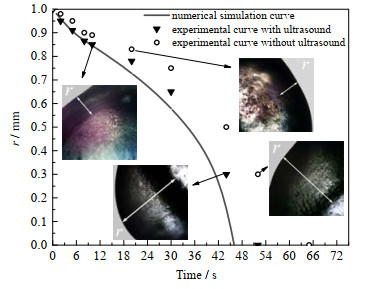
|
图 11 液滴冻结过程中固液交界面随时间的变化规律 Fig.11 Profiles of droplet solid-liquid interface as a function of time |
在声场理论和热质守恒的基础上,建立了超声波作用下液滴冷却冻结数学模型,分析了不同条件下超声波对冻结过程的影响,给出了在液滴冷却冻结过程中超声波空化效应导致传质引起传热量与超声波热效应产热量的变化规律。主要结论为:
(1) 获得了超声波和无超声波作用下液滴冷却冻结过程中直径、温度随时间的变化规律,明确了超声波作用有助于液滴的蒸发冷却。
(2) 超声波空化效应强化了液滴与周围环境的传质,有助于液滴的冷却冻结。当超声波的强度为1 000、700和400 W·m-2时,完全冻结所需时间分别为46、48、54 s。
(3) 揭示了超声波热效应产热量与超声波空化效应导致传质引起传热量的变化规律,确定了超声波辅助冷却冻结的作用时间临界点,为超声波冷却冻结的高效利用提供了依据和参考。
|
|
| [1] |
索原杰, 宣晓婷, 凌建刚, 等. 超声波辅助冻结在水产品及肉类产品中的应用研究进展及解冻机制[J]. 生物加工过程, 2008, 16(3): 77-83. SUO Y J, XUAN X T, LING J G, et al. Application of ultrasonic-assisted freezing and thawing technique for aquatic and meat products[J]. Chinese Journal of Bioprocess Engineering, 2008, 16(3): 77-83. |
| [2] |
陈修平, 夏长所, 李铁山, 等. 放散式体外冲击波与超声波治疗冻伤肩的比较[J]. 中华实验外科杂志, 2013, 30(3): 636-639. CHEN X P, XIA C S, LI T S, et al. A comparison of the effectiveness of radial extracorporeal shock wave therapy and ultrasound therapy on managing frozen shoulder[J]. Chinese Journal of Experimental Surgery, 2013, 30(3): 636-639. DOI:10.3760/cma.j.issn.1001-9030.2013.03.078 |
| [3] |
顾红梅, 张新申, 蒋小萍. 超声波法和冻结-溶解法相结合提取紫薯中花色甙[J]. 食品科学, 2004, 25(7): 104-108. GU H M, ZHANG X S, JIANG X P. Extracting technology on ultrasonic method and frozen-melt method for extracting anthocyanins from purple sweet potato[J]. Food Science, 2004, 25(7): 104-108. DOI:10.3321/j.issn:1002-6630.2004.07.021 |
| [4] |
JORDENS J, GIELEN B, BRAEKEN L, et al. Determination of the effect of the ultrasonic frequency on the cooling crystallization of paracetamol[J]. Chemical Engineering and Processing: Process Intensification, 2014, 84: 38-44. DOI:10.1016/j.cep.2014.01.006 |
| [5] |
WANG S L, SEKERKA R F, WHEELER A A, et al. Thermodynamically-consistent phase-field models for solidification[J]. Physica D: Nonlinear Phenomena, 1993, 69(1/2): 189-200. |
| [6] |
赵凯璇, 赵建福, 陈淑玲, 等. 液滴真空闪蒸/冻结过程的热动力学研究[J]. 空间科学学报, 2011, 31(1): 57-62. ZHAO K X, ZHAO J F, CHEN S L, et al. Thermodynamics of flashing/freezing process of a droplet in vacuum[J]. Chinese Journal of Space Science, 2011, 31(1): 57-62. |
| [7] |
耿县如, 徐庆, 李占勇, 等. 喷雾冷冻法单个液滴冻结过程模拟[J]. 化工进展, 2012, 31(5): 981-986. GENG X R, XU Q, LI Z Y, et al. Numerical simulation of a single droplet freezing process[J]. Chemical Industry and Engineering Process, 2012, 31(5): 981-986. |
| [8] |
吕明, 宁智, 孙春华, 等. 液滴内空泡生长控制机理及影响因素的研究[J]. 高校化学工程学报, 2016, 30(6): 1292-1299. LV M, NING Z, SUN C H, et al. Control mechanism and affecting factors of cavitation bubble growth within a droplet[J]. Journal of Chemical Engineering of Chinese Universities, 2016, 30(6): 1292-1299. DOI:10.3969/j.issn.1003-9015.2016.06.008 |
| [9] |
VIRONE C, KRAMER H J M, VAN R G M, et al. Primary nucleation induced by ultrasonic cavitation[J]. Journal of Crystal Growth, 2006, 294(1): 9-15. DOI:10.1016/j.jcrysgro.2006.05.025 |
| [10] |
MATHIEU S, ROMAN P, JULIEN A. A theoretical model for ice primary nucleation induced by acoustic cavitation[J]. Ultrasonics Sonochemistry, 2010, 17(1): 98-105. DOI:10.1016/j.ultsonch.2009.04.008 |
| [11] |
余德洋. 超声波强化溶液冻结的机理研究[D]. 上海: 上海理工大学, 2012. YU D Y. The study on the mechanism of enhancement of solution crystallization by power ultrasound[D]. Shanghai: University of Shanghai for Science and Technology, 2012. |
| [12] |
MASON T J, PANIWNYK L, LORIMER J P. The uses of ultrasound in food technology[J]. Ultrasonics Sonochemistry, 1996, 3(3): S253-S260. DOI:10.1016/S1350-4177(96)00034-X |
| [13] |
张光明, 常爱敏, 张盼月. 超声波水处理技术[M]. 北京: 中国建筑工业出版社, 2006. ZHANG G M, CHANG A M, ZHANG P Y. Ultrasonic water treatment technology[M]. Beijing: China Building Industry Press, 2006. |
| [14] |
王伟宁, 吕秉玲. 超声波在碱式氯化镁结晶中的应用研究[J]. 无机盐工业, 1990(3): 22-23. WANG W N, LV B L. Application of ultrasonic in the crystallization of basic magnesium chloride[J]. Inorganic Chemicals Industry, 1990(3): 22-23. |
| [15] |
KELLY D R, HARRISON S J, JONES S, et al. Rapid crystallisation using ultrasonic irradiation-sonocrystallisation[J]. Tetrahedron Letters, 1993, 34(16): 2689-2690. DOI:10.1016/S0040-4039(00)77657-X |
| [16] |
FEUILLEBOIS T F, LASEK A, CREISMEAS P, et al. Freezing of a subcooled liquid droplet[J]. Journal of Colloid and Interface Science, 1995, 169(1): 90-102. DOI:10.1006/jcis.1995.1010 |
| [17] |
张跃凯. 液滴真空冻结过程传热传质特性模拟研究[D]. 沈阳: 东北大学, 2015. ZHANG Y K. Simulation study on heat and mass transfer characteristic of droplet vacuum freezing process[D]. Shenyang: Northeastern University, 2015. |
| [18] |
HINDMARSH J P, RUSSELL A B, CHEN X D. Experimental and numerical analysis of the temperature transition of a suspended freezing water droplet[J]. International Journal of Heat and Mass Transfer, 2003, 46(7): 1199-1213. DOI:10.1016/S0017-9310(02)00399-X |
| [19] |
高蓬辉, 衡文佳, 周兴业, 等. 临界条件(0 ℃) 下溶液蒸发冷冻过程中的传质规律[J]. 化工学报, 2013, 64(9): 3206-3212. GAO P H, HENG W J, ZHOU X Y, et al. Mass transfer of liquor in evaporation-refrigeration process under critical condition[J]. CIESC Journal, 2013, 64(9): 3206-3212. |
| [20] |
张翔, 陈军, 林莉, 等. 复合材料孔隙形貌特征对超声波散射衰减影响的分析[J]. 中国机械工程, 2010, 21(14): 1735-1741. ZHANG X, CHEN J, LIN L, et al. Effects on ultrasonic scattering attenuation coefficient of morphological characteristics of voids in composite materials[J]. China Mechanical Engineering, 2010, 21(14): 1735-1741. |
| [21] |
HICKLING R. Nucleation of freezing by cavity collapse and its relation to cavitation damage[J]. Nature, 1965, 206(4987): 915-917. DOI:10.1038/206915a0 |
| [22] |
王葳, 张绍志, 陈光明, 等. 超声波对水的过冷度影响的实验研究[J]. 制冷学报, 2003, 24(1): 6-8. WANG W, ZHANG S Z, CHEN G M, et al. Experimental study of the effects of ultrasound on the supercooling of water[J]. Journal of Refrigeration, 2003, 24(1): 6-8. |




