1 前言
渗透汽化(Pervaporation,PV)是一种新型膜分离技术,具有高效节能、操作方便、过程易于控制等特点,在有机溶剂分离与纯化方面具有广阔的应用前景,是21世纪最有前途的高新技术之一[1]。NaA分子筛膜具有较高的渗透通量、优异的水优先选择性和良好的热化学稳定性,可用于有机溶剂脱水的渗透汽化分离,是近年研究的热点[2~5]。渗透汽化过程中膜层与支撑体层传质机理差别较大,并且进料和渗透侧操作在不同的压力环境,使得该分离过程异常复杂,因而目前研究还主要停留在实验方面,制约了该技术的发展。陈镇等[6]推导并回归了水中脱除VOC的PDMS/PS复合膜渗透汽化串连传质阻力模型,并将计算结果与实验结果的比较发现模型具有较好的精度。Yang等[7]采用分子模拟方法模拟了乙醇/水在silicalite分子筛中吸附和扩散行为,并利用文献推导的计算公式,预测了303 K时水和乙醇纯组分在silicalite分子筛膜上的渗透性。Pera-Titus等[8]将Maxwell-Stefan(MS)理论应用于描述NaA分子筛膜的乙醇/水渗透汽化分离过程,采用吸附扩散机理对传质过程进行了解释。本课题组在前期研究工作[9, 10]中运用分子模拟方法研究了乙醇/水、乙二醇/水体系中单组分及混合组分在NaA分子筛中的吸附-扩散行为,并且基于Fick定律推导了纯组分在分子筛膜中的渗透模型。Farooq和Sato等人[11, 12]研究发现支撑体层对组分渗透传质过程有着显著的影响,支撑体传质阻力减小有利于膜渗透通量的提高。Kapteijin等[13]基于大量实验数据模拟计算了管式支撑体层在渗透汽化总传质过程中的影响,揭示了组分与支撑体间传质机理及压降分布,并证明组分在多孔载体中主要以努森扩散为主。近年来,研究者采用中空纤维陶瓷支撑体制备NaA分子筛膜,获得了高的渗透通量和装填密度[14]。Shao等[15]在不同结构参数的中空纤维支撑体上合成了NaA分子筛膜,揭示出支撑体结构差异对膜渗透通量影响显著。NaA分子筛膜的传质与膜层和支撑体的结构密切相关,揭示两层间匹配关系并优化过程操作参数,对推动中空纤维分子筛膜的实际应用具有重要的意义。
本文针对中空纤维NaA分子筛膜用于乙醇/水的分离,拟构建整体传质数学模型,以普遍化MS方程描述分子筛膜层的传质行为,并以努森扩散和黏性流传递混合传质描述中空纤维支撑体中的传质行为。通过该数学模型定量认识中空纤维载体结构对膜渗透通量的影响,并进一步考察操作温度、渗透侧压强和进料浓度等操作参数对中空纤维NaA分子筛膜传质的影响,期望为中空纤维分子筛膜的工业放大提供参考。
2 数学模型
2.1 分子筛层传质模型
采用普遍化MS方程描述分子筛膜层中多组分渗透过程,其一般表达式如下[16]:
|
$
-{\rho _z}\frac{{{\theta _i}}}{{RT}}\nabla {\mu _i} = \sum\limits_{\begin{array}{*{20}{c}}
{j = 1}\\
{j \ne i}
\end{array}}^n {{\theta _j}\frac{{\left( {{\theta _j}{J_i}-{\theta _i}{J_j}} \right)}}{{{q_{\rm{M}, i}}{D_{ij}}}} + \frac{{{J_i}}}{{{q_{\rm{M}, j}}{D_{iv}}}}} \;\;\;\;\;\;\;i, j = 1, 2, 3 \ldots \ldots ., n
$
|
(1) |
通过热力学系数Γij建立化学位梯度与表面覆盖率梯度之间的关系,如式(2)和式(3)所示:
|
$
\frac{{{\theta _i}}}{{RT}}\nabla {\mu _i} = \sum\limits_{j = 1}^n {\mathit{\Gamma _{ij}}\nabla {\theta _j}}
$
|
(2) |
|
$
\mathit{\Gamma _{ij}} = {\theta _i}\frac{{\partial \ln {P_i}}}{{\partial {\theta _j}}}\;\;\;\;\;\;i, {\rm{ }}j{\rm{ }} = 1, 2, 3 \ldots \ldots ., n
$
|
(3) |
假设吸附组分i的表面覆盖率θi符合扩展Langmuir吸附模型,则有:
|
$
{\theta _i} = \frac{{{q_i}}}{{{q_{\rm{M}, \mathit{i}}}}} = \frac{{{K_i}{P_i}}}{{1 + \sum\limits_{j = 1}^n {{K_j}{P_j}} }}
$
|
(4) |
鉴于分子筛孔道为高规整连通的结构,普遍化MS方程中互扩散系数可以认为趋于无穷大,而分子表面扩散系数(Div)可以通过分子模拟结合爱因斯坦方程获得[17]:
|
$
{D_{iv}} = \frac{1}{{6N}}\mathop {\lim }\limits_{t \to \infty } \frac{d}{{dt}}\sum\limits_{i = 1}^N {\left\langle {{{\left| {{r_i}\left( t \right)-{r_i}\left( 0 \right)} \right|}^2}} \right\rangle }
$
|
(5) |
对于乙醇/水混合组分的渗透汽化过程,假设如下:(1)乙醇和水组分在NaA分子筛膜中的传质属速率控制步骤;(2)水组分在NaA分子筛中有极强的优先吸附性;(3)乙醇/水混合组分在NaA分子筛中饱和吸附量(qM)由分子模拟计算获得。基于以上各式,可获得水和乙醇在NaA分子筛层渗透通量计算公式:
|
$
{J_{{\rm{w, m}}}} = \frac{{{\rho _z}{M_\rm{w}}{D_\rm{w}}(0){q_\rm{M}}}}{{{\delta _z}}}(\frac{{{K_{\mathop{\rm w}\nolimits} }P_{\mathop{\rm w}\nolimits} ^{\rm{f}}}}{{1 + {K_{\rm{w}}}P_{\rm{w}}^{\rm{f}}}}-\frac{{{K_{\rm{w}}}P_{\rm{w}}^{{\mathop{\rm int}} }}}{{1 + {K_{\rm{w}}}P_{\rm{w}}^{{\rm{int}}}}})
$
|
(6) |
|
$
{J_{{\rm{e, m}}}}{\rm{ = }}\frac{{{\rho _z}{M_{\rm{e}}}{D_{\rm{e}}}(0){q_\rm{M}}}}{{{\delta _z}}}(\frac{{1 + {K_{\rm{e}}}P_{\rm{e}}^{\rm{f}}}}{{1 + {K_{\rm{w}}}P_{\rm{w}}^{\rm{f}}}})(\frac{{{K_{\rm{e}}}P_{\rm{e}}^{\rm{f}}}}{{1 + {K_{\rm{w}}}P_{\rm{w}}^{\rm{f}}}}-\frac{{{K_{\rm{e}}}P_{\rm{e}}^{{\rm{int}}}}}{{1 + {K_{\rm{w}}}P_{\rm{w}}^{{\rm{int}}}}}) + \frac{{{M_{\rm{e}}}}}{{{M_{\rm{w}}}}}\frac{{{D_{\rm{e}}}(0)}}{{{D_{\rm{w}}}(0)}}\frac{{{K_{\rm{e}}}P_{\rm{e}}^{\rm{f}}}}{{1 + {K_{\rm{w}}}P_{\rm{w}}^{\rm{f}}}}{J_\rm{w}}
$
|
(7) |
2.2 支撑体层传质模型
中空纤维载体假设为混合均质多孔结构,由于载体侧操作在真空条件下,组分在支撑体中主要以努森扩散和黏性流扩散为主,努森扩散通量计算式如式(8)所示:
|
$
{J_{K\rm{n}, \mathit{i}}} =-\frac{{{M_\mathit{i}}}}{{RT}}{D_{K\rm{n}, \mathit{i}}}\nabla {P_\mathit{i}}\;\;\;\;\;\;\;\;\;{D_{K\rm{n}, \mathit{i}}}{\rm{ = }}\frac{\varepsilon }{\tau }\frac{{{d_p}}}{3}\sqrt {\frac{{8RT}}{{\pi {M_i}}}}
$
|
(8) |
黏性流通量计算式如式(9)所示:
|
$
{J_{\rm{Vis}, \mathit{i}}}{\rm{ = }}-\frac{{{M_i}}}{{RT}}{B_o}\frac{{{{\overline P }_i}}}{\eta }\nabla P\;\;\;\;\;{B_o}{\rm{ = }}\frac{\varepsilon }{\tau }\frac{{{d_p}^2}}{{32}}
$
|
(9) |
基于式(8)与(9),推导得到支撑体层乙醇、水渗透通量计算式如下:
|
$
{J_{{\rm{w, s}}}} = \frac{{\varepsilon {M_{\rm{w}}}}}{{\tau RT{\delta _\rm{s}}}}[\frac{{{d_p}}}{3}\sqrt {\frac{{8RT}}{{\pi {M_{\rm{w}}}}}} (P_{\rm{w}}^{{\rm{int}}}-P_{\rm{w}}^{\rm{p}}) + \frac{{{{\overline P }_{\rm{w}}}d_p^2}}{{32\eta }}(P_{\rm{t}}^{{\rm{int}}}-P_{\rm{t}}^{\rm{p}})]
$
|
(10) |
|
$
{J_{{\rm{e, s}}}} = \frac{{\varepsilon {M_{\rm{e}}}}}{{\tau RT{\delta _\rm{s}}}}[\frac{{{d_p}}}{3}\sqrt {\frac{{8RT}}{{\pi {M_{\rm{e}}}}}} (P_{\rm{e}}^{{\rm{int}}}-P_{\rm{e}}^{\rm{p}}) + \frac{{{{\overline P }_{\rm{e}}}d_p^2}}{{32\eta }}(P_{\rm{t}}^{{\mathop{\rm int}} }-P_{\rm{t}}^{\rm{p}})]
$
|
(11) |
依据串联阻力模型,分子筛膜层的渗透速率与支撑体层渗透速率相等,膜层渗透通量与支撑体层渗透通量满足:Jw, mlout=Jw, s(lout-linn)/㏑(lout/linn)、Je, mlout=Je, s(lout-linn)/㏑(lout/linn)。分别联立式(6)和(10);(7)和(11),采用插值法可计算获得水和乙醇的渗透通量。
3 实验与分析方法
采用渗透汽化膜分离装置对中空纤维NaA分子筛膜分离性能进行表征。以水和乙醇(分析纯,西陇化工股份有限公司)配制成不同浓度的混合物作为原料液,经恒温水浴槽加热至一定温度后通过磁力泵输送至膜组件,膜的另一侧采用真空抽吸的方式使渗透组分透过中空纤维NaA分子筛膜,继而通过液氮环境中的冷阱捕集。原料液和渗透液组成由气相色谱仪(SP6890,山东鲁南瑞虹化工仪器有限公司)进行测定,检测器为热导池检测器(TCD),色谱柱为Porapak-Q填充柱。
陶瓷中空纤维支撑体孔隙率和曲折因子通过自动压汞仪(PoreMater GT60,QUANTACHROME,USA)测得,支撑体孔径由泡压装置(实验室自制)测得。
4 结果与讨论
4.1 乙醇/水混合组分在NaA分子筛膜中的吸附与扩散
4.1.1 吸附参数的计算
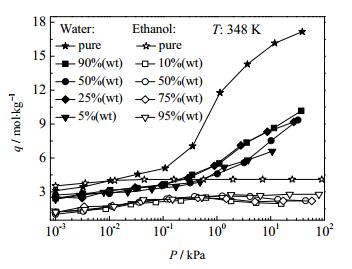
采用巨正则系综蒙特卡洛方法模拟乙醇/水混合组分在NaA分子筛中的吸附行为,揭示乙醇/水混合组分在NaA分子筛中的吸附特性,进而获得渗透模型中模拟所需吸附参数。图 1为348 K时不同进料水含量下乙醇/水混合组分在NaA分子筛中的吸附等温线。在各自分逸度下,混合组分中乙醇和水组分在NaA分子筛中的吸附量均小于各自纯组分状态下的吸附量,随着组分逸度的增大,水的吸附量先缓慢增加,而后呈急剧上升趋势。利用图 1获得的水和乙醇吸附量值,关联式(4)获得不同浓度和温度下水和乙醇组分在NaA分子筛中吸附平衡常数Kw和Ke,如表 1所示。吸附平衡常数随温度增大而减小,随进料浓度变化较小,计算获得348 K时水的吸附平衡常数为(4.48±0.3)×10-4 Pa-1。
表 1(Tab. 1)

表 1 298~373 K时不同浓度下水和乙醇的吸附等温线扩展Langmuir模型拟合参数
Table 1 Fitting results using the extend Langmuir model for water and ethanol mixtures at 298~373 K
| Ki/ 10-4 Pa-1
|
| Water content / %(wt)
|
298 K |
|
323 K |
|
348 K |
|
373 K |
| Kw
|
Ke
|
Kw
|
Ke
|
Kw
|
Ke
|
Kw
|
Ke
|
| 5 |
24.8 |
0.63 |
|
8.4 |
0.19 |
|
4.48 |
0.06 |
|
1.74 |
0.02 |
| 25 |
17.7 |
1.23 |
8.08 |
0.48 |
4.12 |
0.33 |
1.68 |
0.05 |
| 50 |
11.8 |
1.37 |
8.08 |
0.52 |
4.23 |
0.36 |
1.18 |
0.11 |
| 90 |
12.6 |
1.63 |
8.95 |
1.3 |
4.95 |
0.71 |
1.68 |
0.21 |
|
表 1 298~373 K时不同浓度下水和乙醇的吸附等温线扩展Langmuir模型拟合参数
Table 1 Fitting results using the extend Langmuir model for water and ethanol mixtures at 298~373 K |
4.1.2 扩散参数的计算
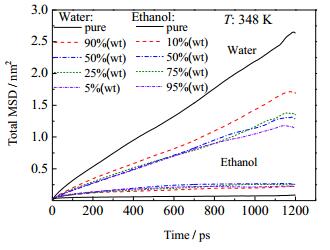
采用平衡态分子动力学方法模拟乙醇/水混合组分在NaA分子筛中的扩散行为。图 2为348 K温度下不同浓度的乙醇/水混合组分在NaA分子筛中的扩散均方位移(MSD)。从图中可以看出混合组分中水的MSD值均小于纯水组分的MSD值,而混合组分中乙醇的MSD值均大于纯乙醇组分的MSD值。这说明混合组分在分子筛中扩散时,组分间的相互作用会显著影响到他们的扩散行为。利用图 2获得的水和乙醇MSD值,关联式(5)获得不同浓度和温度下水和乙醇组分在NaA分子筛中自扩散系数Dw和De,结果如表 2所示。表 2中乙醇和水组分自扩散系数随水含量变化存在一定波动,主要与分子模拟的计算方法有关[18]。该分子模拟过程中,由于不同浓度下吸附的水和乙醇分子均较少,计算获得的Dw和De接近无限稀释状态下的扩散系数Dw(0)和De(0)。
表 2(Tab. 2)

表 2 298~373 K时不同浓度下乙醇/水混合组分在NaA分子筛中的自扩散系数
Table 2 Self-diffusivities of the water/ethanol mixtures in NaA zeolite at 298~373 K
| Di/10-10 m2·s-1
|
| Water content / %(wt)
|
298 K |
323 K |
348 K |
373 K |
| Dw
|
De
|
Dw
|
De
|
Dw
|
De
|
Dw
|
De
|
| 5 |
0.39 |
0.18 |
0.58 |
0.23 |
1.6 |
0.19 |
2.5 |
0.12 |
| 25 |
0.38 |
0.14 |
0.92 |
0.27 |
1.8 |
0.27 |
2.6 |
0.14 |
| 50 |
0.37 |
0.1 |
0.88 |
0.2 |
1.8 |
0.28 |
3.2 |
0.15 |
| 90 |
0.36 |
0.13 |
0.72 |
0.22 |
2.3 |
0.2 |
2.8 |
0.13 |
|
表 2 298~373 K时不同浓度下乙醇/水混合组分在NaA分子筛中的自扩散系数
Table 2 Self-diffusivities of the water/ethanol mixtures in NaA zeolite at 298~373 K |
4.2 不同操作参数对渗透汽化性能的影响
基于分子模拟获得的吸附和扩散参数,通过式(6)和(10);(7)和(11)计算出不同操作参数条件下的中空纤维NaA分子筛膜中水和乙醇的渗透通量,用于计算的中空纤维NaA分子筛膜微结构参数(孔隙率、曲折因子、孔径)由实验测得,而NaA分子筛密度由文献[8]中获得,如表 3所示。
表 3(Tab. 3)

表 3 模型相关参数取值
Table 3 Parameters used in the mass transfer model simulation
| Parameter |
Value |
| Porosity of the support layer, ε
|
0.65 |
| Tortuosity of the support layer, τ
|
2 |
| Thickness of the support layer, δs / m |
4×10-4
|
| Pore diameter of the support layer, dp / m |
5.6×10-7
|
| Density of zeolite NaA, ρz / kg·m-3
|
1900 |
| Thickness of the zeolite layer, δz / m |
5×10-6
|
|
表 3 模型相关参数取值
Table 3 Parameters used in the mass transfer model simulation |
4.2.1 进料温度的影响
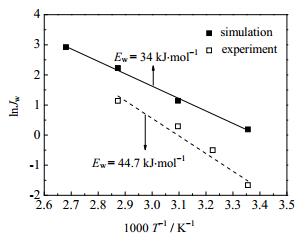
基于模型计算水通量与温度之间的Arrhenius关系如图 3所示,进料水含量为5 %(wt)。为了验证模型的可靠性,图中给出了相应条件下渗透汽化实验结果。可以看出,模拟与实验的水通量均随温度升高而不断增大。这是因为,进料温度的升高,水组分逸度增大,水在分子筛中吸附量不断升高,同时水的扩散系数也在不断增大(如表 2所示)。模拟得到的水通量约是实验值3倍,两者间的差异主要是由于实际过程中分子筛层的晶间缺陷,及中空纤维支撑体包含海绵层和指状孔,而模拟计算的水通量是基于完美无缺陷的分子筛层和混合均质的支撑体层。根据图 3结果,基于模型和实验获得的水渗透活化能分别为34和44.7 kJ·mol-1,二者与文献报道结果接近[8, 19],模型计算结果相对较低可能原因是实验中水分子在NaA分子筛膜中渗透过程尚未处于完全的平衡状态。
4.2.2 进料浓度的影响
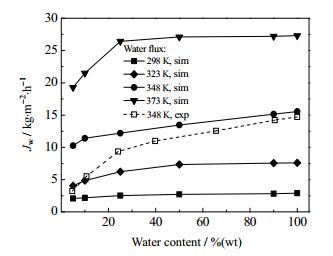
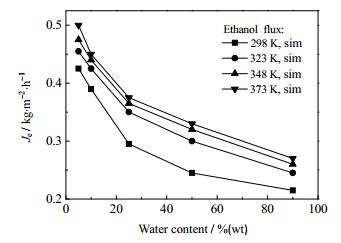
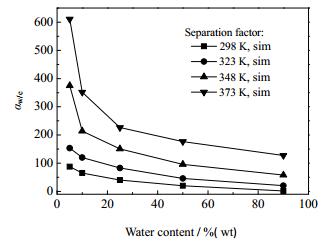
图 4和5分别为进料浓度对中空纤维NaA分子筛膜水通量和乙醇通量的影响结果。随进料水含量的增加,348 K时水通量的实验值与模拟值均呈增大趋势,而乙醇的通量呈减小趋势。由于NaA分子筛膜的渗透服从吸附-扩散机理,在一定温度下,随着料液乙醇浓度降低和水含量的增大,NaA分子筛膜表面的水吸附量不断增加,导致膜的水通量增大。当进料水含量增加到一定水平后,分子筛膜的水吸附量趋于饱和,膜的渗透通量趋于平缓。从图中可以看出,在较高进料水含量下,膜的水通量随温度的增长趋势较为明显。这是由于温度升高带来膜吸附系数减小,膜表面水吸附量需要在较高的进料浓度下才能达到饱和吸附。由于温度升高有利于组分在膜孔内的扩散,因此,尽管同样处于饱和吸附,高温操作亦能够提高膜渗透通量。从图 4中还可以看出,通过模拟计算得到的水纯组分通量随着温度升高而不断增大,这种变化趋势与本课题组前期研究工作[9]获得的实验结果一致,这是由于纯组份饱和蒸汽压随着温度的升高而不断增大。图 6为对应图 4和图 5中不同温度和进料浓度下乙醇/水混合组分的分离因子。可以看出,分离因子随水含量增大呈减小趋势。该计算结果与文献报道[8]类似,这主要是因为当水含量高于一定值时,膜进料水吸附量趋于稳定,而带来渗透侧分离组分变化较小。由图 4可以看出,分离因子的模拟值低于实验值,这可能是因为模拟过程中水吸附量低于实际值而带来所计算的乙醇渗透通量偏大。
4.2.3 渗透侧压强的影响
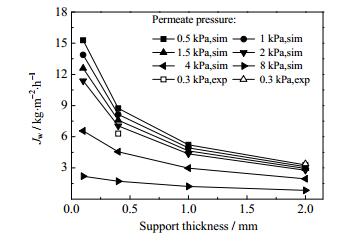
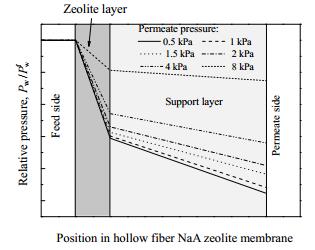
图 7为不同支撑层厚度下,计算获得348 K下乙醇/水混合组分在进料水含量为5%(wt)时水通量随渗透侧压强的变化关系。可以看出,随着渗透侧压强的升高,水通量逐渐减小,这与跨膜传质推动力的减少有关。另一方面,随着支撑体厚度的减少,水通量相应增加,表明支撑体的传质阻力对渗透通量存在一定的影响。然而,在较低的渗透侧压强下,支撑体厚度对水通量的影响变得十分显著。这是因为,对于渗透汽化过程,由于渗透侧压强的减少,分子的平均自由程增加,导致支撑体孔道中分子与壁面碰撞频率增加,支撑体结构对水的传质影响增强。在渗透侧压强为0.3 kPa的实验条件下,考察进料水含量为10%(wt)时水通量随支撑体厚度变化的情况,结果表明,随着支撑体厚度从2 mm降低到0.4 mm,水通量从3.06 kg·m2·h-1上升至6.84 kg·m2·h-1。由图 7可以看出,模拟结果与实验结果吻合较好。为了进一步揭示支撑体传质阻力的影响,模型进一步研究了不同渗透侧压强下水组分在中空纤维膜断面压降分布,如图 8所示,膜层和支撑层相关参数如表 3所示,进料水含量为5%(wt),温度为348 K。可以看出,在较高的渗透侧压强下,支撑体中水分压的压降较小,表明膜传质阻力主要集中在分子筛膜层。然而,模拟结果显示,当渗透侧压强降低到1 kPa时,支撑体中水分压压降明显提高,表明其传质阻力对水通量产生明显影响。此时,采取措施降低支撑体的传质阻力对提高膜渗透通量将产生显著影响。对于中空纤维分子筛膜,在减小支撑体厚度的同时,优化载体的孔径分布、孔隙率等结构参数有望进一步提高膜渗透通量。
5 结论
本文采用普遍化MS方程和努森、黏性流混合扩散方程,构建了中空纤维NaA分子筛膜的整体传质模型,并用于乙醇/水的渗透汽化过程模拟。该模型能很好地反映操作参数对渗透通量的影响规律,研究显示增加进料水含量、提高操作温度及减小渗透侧压强可以提高水通量。模拟发现,渗透汽化过程中支撑体传质阻力对水渗透通量产生影响,渗透侧压强低于1 kPa时,该影响更为显著。研究结果证实了采用中空纤维支撑体制备的分子筛膜能够显著提高膜渗透通量。本模型计算的渗透通量高于实验过程所获得的渗透通量,可能与实际过程中分子筛层的晶间缺陷,以及模型假设支撑体为混合均质层有关。为了进一步优化中空纤维支撑体的结构,在后续工作中,数学模型还需要考虑载体的孔径分布对膜渗透通量的影响。
符号说明:
Bo -黏性流扩散系数,m2·h-1
dp -孔径,m
Dij -MS互扩散系数,m2·h-1
Div -MS自扩散系数,m2·h-1
DKn -努森扩散系数,m2·h-1
l -半径,m
J -渗透通量,kg·m2·h-1
K -吸附平衡常数,Pa-1
Kn -努森扩散系数,m2·h-1
N -扩散分子数
P -平均压强,Pa
q -吸附量,mol·kg-1
qM -饱和吸附量,mol·kg-1
r -位移,m
δ -厚度,m
ε -孔隙率
η -黏度,Pa·s
θ -覆盖率
Γij -热力学因子
μ -化学势,kJ·mol-1
ρ -密度,kJ·mol-3
τ -曲折因子
上标
f -进料侧
int -膜层/支撑体层界面处
p -渗透侧
下标
e -气泡
c -乙醇
inn -支撑体内径,m
m -分子筛层
out -支撑体外径,m
s -支撑体层
t -乙醇+水
Vis -黏性流
w -水
z -分子筛层