2. 合肥工业大学 化学与化工学院,安徽 合肥 230009;
3. 安徽省农业科学院 棉花研究所,安徽 合肥 230001
2. School of Chemistry and Chemical Engineering, Hefei University of Technology, Hefei 230009, China;
3. Cotton Research Institute of Anhui Academy of Agricultural Sciences, Hefei 230001, China
我国是一个农业大国,化肥的生产和消费量排世界第一,约占世界各国总量的1/3。肥料利用率不高是目前我国农业生产中存在的一个严重问题,不仅是农业问题,也是环境、资源和能源问题[1]。研究与开发高利用率的绿色无污染环保肥料迫在眉睫。缓/控释肥料是指能够延缓或调节肥料养分的释放强度与速率,使其与作物生长所需养分同步的肥料[2-4]。近年来,我国聚合物包膜缓/控释肥料发展迅速,截止到2019年03月25日,农业部发布有效登记的缓释肥料产品只有30个,其中28个为包膜尿素。目前,低成本的可生物降解聚合物包膜材料是该领域的研究热点。聚乳酸(PLA)是一种新型可生物降解环境友好型的热塑性脂肪族聚酯材料,具有加工性能好、可塑性强和热稳定性高等优点,已广泛应用于医疗卫生、服装和包装材料等领域[5-6]。近年来,美国以玉米为原料工业的发展极大降低了PLA的生产成本,使之成为当前市场上售价最低的可生物降解合成高分子材料之一。
影响聚合物包膜缓/控释肥料养分释放的因素很多,为了评价方便,通常以水为介质研究聚合物包膜肥料养分的释放特征。RABAN和ZAIDEL等[7]对聚合物包膜肥料的养分释放机理进行了研究,其成果有力地推动了缓/控释肥料养分释放的理论研究,但是其模型太复杂,缺乏通用性。SHAVIV[8]和杜昌文等[9]以Fick第二定律为基础研究了聚合物包膜肥料中钾素的分段释放特征;张保林等[10]为了研究聚合物包膜控释肥料的养分释放机制,建立了聚合物包膜控释肥料氮素释放的数学模型,这些模型的应用都是假设恒温条件。本文以Shaviv模型为基础,选用尿素作为模型肥料、PLA作为模型包膜材料,采用溶液浇铸法制备聚乳酸薄膜、流化床包膜法制备包膜尿素颗粒。分别利用Ussing chamber方法和田间试验法测定聚乳酸膜的渗透系数和聚乳酸包膜尿素颗粒在土壤中的养分释放特征。以肥料在土壤中的真实环境为依据设计模型参数,以聚乳酸包膜尿素在土壤中释放性能为考核指标,建立聚乳酸包膜尿素养分释放模型。期望对包膜材料的研究、包膜颗粒肥料的设计与应用具有良好的指导作用。
2 实验(材料与方法) 2.1 实验材料与仪器PLA 3051D,苏州优利科技材料有限公司;电子分析天平(BSA124S-CW,德国赛多利斯);高速均制机(T18,德国IKA仪科);可见分光光度计(VIS-722,上海精隆科学仪器)。
2.2 聚乳酸薄膜及包膜尿素制备称取一定量的PLA溶解于溶剂中得到PLA包膜液,采用(1)溶液浇铸法制备聚乳酸薄膜,膜厚控制(47±10) μm;(2)流化床包膜法制备包膜尿素,尿素粒径为(6±0.1) mm,包膜厚度为(47±10) μm。
2.3 聚乳酸薄膜氮养分和水蒸汽渗透系数的测定采用SUN和YAO等[10]报道的Ussing chamber方法测定尿素饱和溶液中尿素(以氮计)养分对于PLA薄膜的渗透系数PS。装置如图 1所示,PLA薄膜用球磨夹1固定,形成供给池2 (donor cell)与接收池2 (receptor cell)之间唯一通道。实验开始时,在供给池中加入200 mL尿素过饱和溶液,接收池中加入200 mL蒸馏水。每天(24 h)从接收池取样2 mL,紫外分光光度法测定氮含量,同时向接收池中补充2 mL蒸馏水,供给池和接收池置于同一恒温系统中。
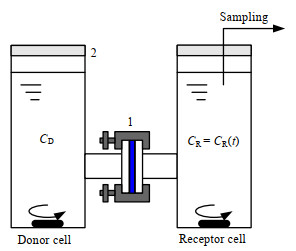
|
图 1 氮养分渗透系数测定装置 Fig.1 Schematic diagram of the experimental setup for the measurement of permeability coefficient of N-nutrient |
稳态传质条件下,尿素饱和溶液中氮养分通过PLA薄膜的渗透系数PS计算式为:
| ${P_{\rm{S}}} = \frac{V}{A}\frac{l}{{{C_{\rm{D}}} - {C_{\rm{R}}}}}\frac{{{\rm{d}}{C_{\rm{R}}}}}{{{\rm{d}}t}}$ | (1) |
其中,V为接收池中溶液体积,mL;l为膜厚,cm;A为透膜面积,cm2;t为时间,d;CD为供给池中氮养分浓度,g·cm-3,即尿素饱和溶液浓度;CR为接收池中氮养分浓度,g·cm-3;
由于CR < < CD,故CD-CR ≈ CD。所以式(1)可简化为,
| ${P_{\rm{S}}} = \frac{{Vl}}{{A{C_{\rm{D}}}}}\frac{{{\rm{d}}{C_R}}}{{{\rm{d}}t}}$ | (2) |
水蒸汽对PLA薄膜的渗透系数Ph采用GUERIN和BRIAND等[12]的测定方法,如图 2所示。该装置由两个相同密封单元2通过球磨夹连接组成,置于同一恒温系统中,PLA薄膜用球磨夹1固定,3号瓶内装有蒸馏水,4号瓶内为变色硅胶干燥剂,薄膜左右两侧单元会形成压力差,此压差即为水蒸汽的渗透压。渗透到右边单元的水蒸汽被变色硅胶吸收。每隔24 h使用电子分析天平对4号瓶称重,水蒸汽通过PLA薄膜的渗透系数Ph的计算式为:
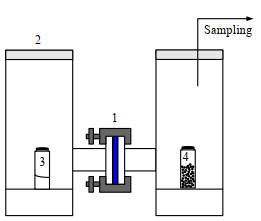
|
图 2 水蒸汽渗透系数测定装置 Fig.2 Schematic diagram of the experimental setup for the measurement of water vapor |
| ${P_{\rm{h}}} = \frac{l}{{A{\rho _{\rm{w}}}\Delta P}}\frac{{{\rm{d}}w(t)}}{{{\rm{d}}t}}$ | (3) |
其中Ph为水蒸汽的渗透系数,cm2·Pa-1·d-1;l为膜厚,cm;A为透膜面积,cm2;ΔP是膜两边的蒸压差,Pa;ρw为水的密度,g·cm-3。
2.4 模型的选择与应用根据SHAVIV等[7-8, 13-16]提出的球形包膜肥料颗粒养分释放数学模型,包膜肥料颗粒在土壤中养分的释放分为滞后期、匀速期和衰减期3个阶段:
(1) 滞后期
| $g(r, l, t) = {0}\;\;\;\;\;\;\;\;t \leqslant t' $ | (4) |
(2) 匀速期
| $g(r,l,t) = \frac{{3{P_{\rm{S}}}{C_{{\rm{sat}}}}}}{{rl{\rho _{\rm{s}}}}}(t - t')\;\;\;\;t' \le t \le t'' $ | (5) |
(3) 衰减期
| $1 - \frac{{{C_{{\rm{sat}}}}}}{{{\rho _{\rm{s}}}}}{\rm{exp}}[ - \frac{{3{P_{\rm{S}}}}}{{rl}}(t - t')]\;\;\;\;t>t'' $ | (6) |
| $t'' = \frac{{\gamma V}}{{\frac{{{P_{\rm{h}}}}}{l}A\Delta P}} = \frac{{\gamma tl}}{{3P\Delta P}}$ | (7) |
| $t'' = t' + (1 - \frac{{{C_{{\rm{sat}}}}}}{{{\rho _{\rm{s}}}}})\frac{{rl{\rho _{\rm{s}}}}}{{3{P_{\rm{S}}}{C_{{\rm{sat}}}}}} $ | (8) |
对于确定的包膜材料,在肥料确定的条件下(即ρs和Csat已知),测试获得渗透系数PS和Ph后,则可以对不同颗粒半径r和包膜厚度l的包膜肥料的养分释放性能进行预测。
2.5 包膜尿素田间试验设计该试验于2018年6月22日~10月25日在安徽省东至县大渡口镇进行,试验作物为棉花,供试品种为“中棉所915”,生育期为121天。采用埋袋法(深度为10~15 cm)测定聚乳酸包膜尿素氮养分释放特征。同时进行2组平行试验,称取一定量的包膜尿素,装入网袋(15 cm × l0 m,孔径为1.0 mm)中并封口,网袋用纱布包裹。在棉花行中间挖一条深15 cm、宽12 cm的沟,将网袋平铺在沟底,并使网袋中的肥料颗粒均匀散开,覆土至沟平。每隔一定时间取出肥料网袋,去掉纱布外包装,倒入2.0 mm土壤筛中,在盛满水的量杯中轻轻摆动土壤筛,直至洗净泥土;将剩余肥料全部碾碎、充分溶解和过滤,滤液及洗涤液全部转入500 mL的容量瓶中定容。采用对二甲氨基苯甲醛分光光度法测定氮含量,并计算出网袋中肥料含氮量及氮养分释放量[17]。
3 实验结果与讨论 3.1 氮养分和水蒸气的透膜渗透系数不同温度下,接收池中氮养分浓度与时间关系如图 3所示,变色硅胶吸收的水蒸气质量与时间关系如图 4所示。
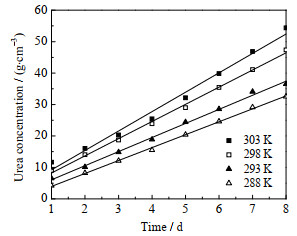
|
图 3 透过聚乳酸薄膜的氮养分含量与时间关系 Fig.3 Relationship between nitrogen nutrient content and time |
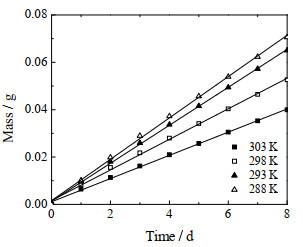
|
图 4 透过聚乳酸薄膜的水蒸汽质量与时间关系 Fig.4 Relationship between water vapor and time |
根据图 3和图 4分别得出
|
|
表 1 氮养分与水蒸气透过聚乳酸薄膜的渗透系数 Table 1 Permeability coefficients of N-nutrient and water vapor through the PLA membrane |
由表 1可知,尿素饱和溶液中氮养分对于PLA薄膜的渗透系数PS和水蒸汽对PLA薄膜的渗透系数Ph是随着温度的变化而变化的。从温度每相差5度的变化率可知,温度对PS和Ph的影响比较大。
3.2 聚乳酸包膜尿素田间的氮养分释放特征由田间试验得到聚乳酸包膜尿素在棉花田间氮养分释放特征,如图 5曲线a、b所示。其中,a、b为平行试验,养分释放结果比较接近,释放80%氮养分的时间均在120~125 d。
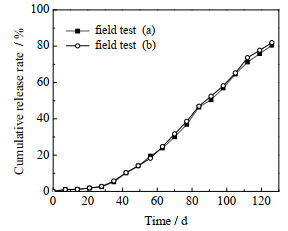
|
图 5 聚乳酸包膜尿素田间试验氮养分累积释放曲线 Fig.5 Cumulative release profiles of N-nutrient from the poly lactic acid coated urea in field tests |
本研究中,尿素颗粒半径r为0.3 cm,包膜厚度l为50 μm,颗粒的密度ρs为1.335 g·cm-3,有效颗粒孔隙率为0.05[7],Csat为不同温度尿素饱和溶液的浓度。将以上参数和表 1中数据代入式(4)、(5)和(6),得到不同温度下包膜尿素颗粒中氮养分的累积释放曲线如图 6所示。图 6中田间试验曲线是图 5平行试验的平均结果。
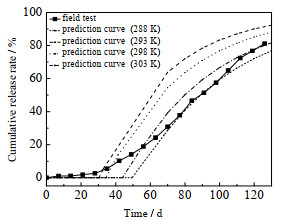
|
图 6 聚乳酸包膜尿素模型预测氮养分累积释放曲线 Fig.6 Prediction results of N-nutrient release from the PLA-coated urea using an isothermal model |
图 6表明,聚乳酸包膜尿素模型预测的氮养分累积释放曲线呈现“S”型,288、293、298和303 K时释放80%的氮养分分别需要139、125、108和95 d,表明温度对模型预测影响较大,且与田间试验氮养分累积释放性能有一定差异,因此,需要根据肥料施用期间环境温度的变化分段采用模型预测。
3.4 聚乳酸包膜尿素分段模型预测的氮养分释放特征根据田间试验期间试验地区日平均气温相差5 ℃为一段分成4段进行模型预测,分段方式如表 2,分段模型预测的氮养分释放特征如图 7所示。由图 7可见,分段模型预测结果与田间试验平均结果吻合程度较好,平均绝对偏差和平均相对偏差分别为1.74%和3.01%。
|
|
表 2 分段方式表 Table 2 Segmental experimental design |
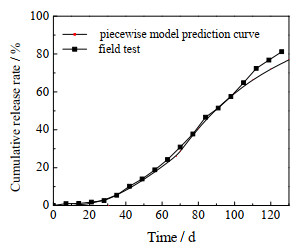
|
图 7 聚乳酸包膜尿分段模型预测氮养分累积释放曲线 Fig.7 Prediction results of N-nutrient release from the PLA-coated urea using an isothermal model |
聚乳酸包膜尿素在田间试验中累积释放率最高为82%,其对应释放时间为125 d左右。由于原始Shaviv模型是针对恒温条件下聚合物包膜肥料颗粒中肥料养分的释放情况,因此其预测结果与田间试验结果相差较大。这是由于在田间试验过程中,环境温度是波动的。根据环境温度变化对田间试验进行分段,并在各段中采用平均温度及其相关参数进行分段模拟的计算结果与实际的田间试验结果吻合较好,可作为一种有效方法指导包膜材料的研发以及包膜颗粒肥料的设计与应用。
3.5.2 数学模型预测偏差分析分段数学模型预测与田间试验释放结果的偏差主要来源于:(1)土壤环境温度的波动情况非常复杂,不同日期、同一日期不同时刻均存在温度变化,数学模型不可能细化到每一时刻,使用日平均温度不可避免存在偏差;(2)肥料养分的渗透系数与其在水溶液中的浓度有关。模型中采用了分段温度下的饱和浓度,而田间试验时膜内浓度会随实际环境发生细微变化,尤其在衰减期表现更明显。
4 结论本研究中,采用聚乳酸作为包膜材料,得到释放期为4个月的聚乳酸包膜尿素,在田间试验中分别在28和124 d内释放了4.1%和80%的养分。根据Shaviv模型,结合实验室测定的PLA薄膜渗透系数等数据,采用分段模拟的方法可比较准确的预测聚乳酸包膜尿素在大田试验中的释放特征,同时根据不同作物的生长周期调节薄膜厚度,对聚合物包膜材料的开发和筛选以及包膜颗粒肥料的设计与应用具有一定的指导意义。
符号说明:
A —传质面积,cm2 PS —溶质的渗透系数,cm2·d-1
Csat —肥料颗粒内部饱和溶液初始浓度,g·cm-3 r —肥料颗粒的半径,cm
l —膜厚,cm ρs —颗粒密度,g·cm-3
ΔP —压差,Pa ρw —水密度,g·cm-3
Ph —水蒸气的渗透系数,cm2·Pa-1·d-1 γ —颗粒孔隙率
| [1] |
李国, 黄春波, 郑淑清, 等. 农业可持续发展中土壤肥料存在的问题与对策思考[J]. 农业与技术, 2018, 38(2): 55-55. LI G, HUANG C B, ZHENG S Q, et al. Problems and countermeasures of soil fertilizers in sustainable agricultural development[J]. Journal of Agriculture and Technology, 2018, 38(2): 55-55. |
| [2] |
杨越超, 耿毓清, 张民, 等. 膜特性对包膜控释肥养分控释性能的影响[J]. 农业工程学报, 2007, 23(11): 23-30. YANG Y C, GENG Y Q, ZHANG M, et al. Effect of membrane characteristics on nutrient controlled release performance of coated controlled release fertilizer[J]. Transactions of the Chinese Society of Agricultural Engineering, 2007, 23(11): 23-30. DOI:10.3321/j.issn:1002-6819.2007.11.004 |
| [3] |
皱洪涛.环境友好型包膜缓释肥料研制及其养分控释机理的研究[D].沈阳: 沈阳农业大学, 2007. ZHOU H T. Development of environment-friendly coated slow-release fertilizers and study on the mechanism of nutrient controlled release[D]. Shenyang: Shenyang Agricultural University, 2007. |
| [4] |
TIAN X, LI C, ZHANG M, et al. Controlled release urea improved crop yields and mitigated nitrate leaching under cotton-garlic intercropping system in a 4-year field trial[J]. Soil and Tillage Research, 2018(175): 158-167. |
| [5] |
王敏, 秦春君, 于海. PLA对土壤微生物生长的影响及PLA的生物降解性[J]. 环境工程学报, 2012, 6(11): 4240-4244. WANG M, QIN C J, YU H. Effect of PLA on soil microbial growth and biodegradability of PLA[J]. Journal of Environmental Engineering, 2012, 6(11): 4240-4244. |
| [6] |
QIN S, WU Z, RASOOL A, et al. Synthesis and characterization of slow-release nitrogen fertilizer with water absorbency:Based on poly (acrylic acid-acrylic amide) Na-bentonite[J]. Journal of Applied Polymer Science, 2012, 126(5): 1687-1697. DOI:10.1002/app.37007 |
| [7] |
SHAVIA A, RABAN S, ZAIDEL L. Modeling controlled nutrient release from polymer coated fertilizers:Diffusion release from single granules[J]. Environmental Science and Technology, 2003, 10(37): 2251-2256. |
| [8] |
DU C, ZHOU J, SHAVIV A, et al. Mathematical model for potassium release from polymer-coated fertilizer[J]. Biosystems Engineering, 2004, 88(3): 395-400. DOI:10.1016/j.biosystemseng.2004.03.004 |
| [9] |
杜昌文, 周健民, 王火焰, 等. 聚合物包膜NPK复合肥料养分释放滞后期的研究[J]. 植物营养与肥料学报, 2005, 11(2): 179-182. DU C W, ZHOU J M, WANG H Y., et al. Study on the lag period of nutrient release in polymer coated NPK compound fertilizer[J]. Journal of Plant Nutrition and fertilizers, 2005, 11(2): 179-182. DOI:10.3321/j.issn:1008-505X.2005.02.007 |
| [10] |
陈可可, 张保林. 聚合物包膜控释肥料氮素释放的数学模拟[J]. 农业工程学报, 2013, 29(9): 123-130. CHEN K K, ZHANG B L. Mathematical simulation of nitrogen release in polymer coated controlled release fertilizer[J]. Journal of Agricultural Engineering, 2013, 29(9): 123-130. |
| [11] |
SUN Y M, HUANG W F, CHANG C C. Spray-coated and solution-cast ethylcellulose pseudolatex membranes[J]. Journal of Membrane Science, 1999, 157(2): 159-170. |
| [12] |
DEVASSINE M, HENRY F, GUERIN P, et al. Coating of fertilizers by degradable polymers[J]. International Journal of Pharmaceutics, 2002, 242(1): 399-404. |
| [13] |
SHAVIA A. Advances in controlled-release fertilizers[J]. Advances in Agronomy, 2001, 71(1): 1-49. |
| [14] |
DU C W, ZHOU J M, SHAVIV A. Release characteristics of nutrients from polymer-coated compound controlled release fertilizers[J]. Journal of Polymers and the Environment, 2006, 14(3): 223-230. |
| [15] |
DU C W, TANG D, ZHOU J M, et al. Prediction of nitrate release from polymer-coated fertilizers using an artificial neural network model[J]. Biosystems Engineering, 2008, 99(4): 478-486. DOI:10.1016/j.biosystemseng.2007.12.003 |
| [16] |
刘志刚, 赵庆良, 孙丽欣, 等. PDAB比色法直接测定液相中的常量尿素[J]. 哈尔滨工业大学学报, 2008, 40(8): 1214-1217. LIU Z G, ZHAO Q L, SUN L X, et al. PDAB colorimetric method for direct determination of constant urea in liquid phase[J]. Journal of Harbin Institute of Technology, 2008, 40(8): 1214-1217. DOI:10.3321/j.issn:0367-6234.2008.08.008 |




