Kriging模型是一种常见的代理模型,最早是一种地质分析中求最优、线形、无偏的空间内插方法[1],后被延伸到数值计算领域,用于数据的插值分析。由于其训练样本的无偏性和高度的非线性等特点,在化工过程中也得到了广泛的应用。Quirante等[2]使用Kriging代理模型取代蒸馏塔,用优化策略对代理模型进行寻优,找到信任区域内的模型局部最优值,解决了蒸馏塔的经济设计问题。王晓强等[3]将Kriging模型应用到自适应差分进化算法中,改善算法的寻优速度和性能,并将改进后的算法应用到苯乙烯装置的流程优化,降低了操作费用。王梦寒等[4]将Kriging模型和遗传算法结合提出一种新型工艺优化参数策略,提高了高光无痕注塑成型制品的综合品质。
然而,Kriging模型也有一定的局限性,在计算成本受限的情况下,由于参数搜索算法的不足,传统的Kriging模型难以建立满足精度要求的模型。同时Kriging模型只依赖于历史数据或实时数据,对一些可以明确的机理信息没有加以合理的应用,造成了一定的资源浪费。本文针对这些局限性,提出一种基于进化算法的模型参数搜索方法,在搜索过程中将模型机理信息的先验检验结果作为过程建模约束条件,利用智能算法搜索模型参数最优解。该方法能同时充分利用样本信息和机理信息 (单调性、凹凸性等),提高Kriging模型的预测能力,有助于改进模型的精度及外延性。
2 基于AEA种群优化算法的Kriging模型 2.1 Kriging模型Kriging模型由线性回归部分和非参数部分组成,其一般表达式为[5]:
| $y(x)={{f}^{T}}(x)\beta +z(x)$ | (1) |
其中f T (x)β为实际响应的全局回归模型,
zx是根据数据的观测及其相关性量化建立的一个高斯随机响应过程,服从:
| $\left\{ \begin{matrix} E(z(x))=0 \\ Var[z(x)]={{\sigma }^{2}} \\ \end{matrix} \right.$ | (2) |
采样点之间的协方差可表示为:
| $Cov[z(\omega ),z(x)]={{\sigma }^{2}}R(\theta ,\omega ,x)$ | (3) |
式中,R(θ, ω, x) 为带有相关性参数θ的相关函数,决定了点之间的空间相关性。Kriging模型常用的相关函数有指数函数,高斯函数,样条函数等。为了保证输出模型的平滑性,本文所选相关函数为高斯函数,其形式如下:
| $R(\theta ,\omega ,x)=\prod\limits_{j=1}^{n}{{{R}_{j}}({{\theta }_{j}},{{\omega }_{j}}-{{x}_{j}})}$ | (4) |
| ${{R}_{j}}({{\theta }_{j}},{{\omega }_{j}},{{x}_{j}})=\exp [-\sum\limits_{j=1}^{n}{{{\theta }_{j}}{{\left| {{\omega }_{j}}-{{x}_{j}} \right|}^{2}}}]$ | (5) |
其中ωj,xj为训练样本点对应的第j个分量。
假设任意一个点x的响应值由已知训练样本的响应值的线性组合来近似,可以表示为:
| $\hat{y}(x)={{c}^{T}}Y$ | (6) |
则近似的误差可以表示为:
| $\begin{align} & \hat{y}(x)-y(x)={{c}^{T}}Y-y(x) \\ & ={{c}^{T}}(F\beta +Z)-({{f}^{T}}(x)\beta +z(x)) \\ & ={{c}^{T}}Z-z(x)+{{({{F}^{T}}c-f(x))}^{T}}\beta \\ \end{align}$ | (7) |
Kriging给出的是实际过程的最小方差无偏估计,要求在无偏的前提下,寻求方差的最小值,即:
| $\begin{align} & \begin{matrix} \min & Var[\hat{y}(x)-y(x)] \\ \end{matrix} \\ & \begin{matrix} s.t. & E[\hat{y}(x)-y(x)] \\ \end{matrix}=0 \\ \end{align}$ | (8) |
用拉格朗日乘子法可解得:
| $c={{R}^{-1}}(r-F{{({{F}^{T}}{{R}^{-1}}F)}^{-1}}({{F}^{T}}{{R}^{-1}}r-f))$ | (9) |
对于未知点x0处的预测值为:
| $\hat{y}({{x}_{\text{0}}})={{f}^{T}}(x)\hat{\beta }+{{r}^{T}}(x){{R}^{-1}}(Y-F\hat{\beta })$ | (10) |
其中r为未知点与样本点之间的相关性向量,定义为:
| $r{{({{x}_{0}})}^{T}}=[R(\theta ,{{x}_{0}},{{x}^{1}}),R(\theta ,{{x}_{0}},{{x}^{2}}),...,R(\theta ,{{x}_{0}},{{x}^{m}})]$ | (11) |
此时线性回归参数和方差估计可通过下式得出:
| $\hat{\beta }={{({{F}^{T}}{{R}^{-1}}F)}^{-1}}{{F}^{T}}{{R}^{-1}}Y$ | (12) |
| ${{\delta }^{2}}=\frac{1}{m}{{(Y-F\hat{\beta })}^{T}}{{R}^{-1}}(Y-F\hat{\beta })$ | (13) |
因为z(x) 服从正态分布,则y(x) 也服从正态分布,要搜索使似然函数取极大值的参数θ。简化后的似然函数可表示为:
| $\text{max}(-\frac{(m\ln ({{\sigma }^{2}})+\ln \left| R \right|)}{2})$ | (14) |
其中m为样本点个数。
根据公式 (14) 定义关于θ的函数:
| $\text{g}(\theta )=\frac{n\ln ({{\sigma }^{2}})+\ln \left| R \right|}{2}$ | (15) |
相关性参数θ的求解过程可看作函数gθ的最小化优化过程。
2.2 Kriging模型参数寻优算法Kriging模型可以精确预测试验点的响应值,并提供在未知点处的预测的不确定性值[6]。同时,对于高斯相关函数,可以通过调整参数θ的值来调整协方差矩阵,进而改变采样策略。构造Kriging模型的关键在于对参数θ的求解。在相关函数R(θ, ω, x) 中θ越大,则ω点和x之间的相关性越弱,模型的非线性程度越大。Lophaven[7]提出了模式搜索算法 (Pattern Search Algorithm) 来求解参数θ,这一方法和相关的DACE工具箱得到了广泛的应用。模式搜索算法是一种解决优化问题的直接方法,在计算时不需要目标函数的导数,只需要给定一个初始解,设置合理的步长进行探索和移动找到更优的解,直到达到终止条件。模式搜索算法简单高效,尤其在处理目标函数不可导或求导麻烦时异常有效,但缺陷是初始值对优化结果的影响较大,由于模型的非线性程度不可明确预知,难以通过经验给定一个合理的初值,而对于一个随机给定的初值,由它求出的参数可能并不是最优的。
针对模式搜索算法的局限性,本文对Kriging模型的参数求解算法进行了改进,选取一种进化优化算法--AEA算法来搜索Kriging模型的参数。AEA算法 (Alopex-based evolutionary algorithm) 最初由李绍军[8]提出,是一种并行搜索算法,不仅一个可行解的所有变量发生改变,而且一个种群中所有个体 (可行解) 的所有变量进行迭代更新。首先随机在解空间内产生两个种群,初始种群和对比种群,种群中每个个体代表一个可行解。利用对比种群和初始种群中对应的个体之间的向量差,以随机的步长从初始个体产生一个中间个体,变量根据一定的概率进行更优或者更差的方向行走。如果产生的中间个体优于原初始个体,则取代初始个体,否则,初始个体不做改变。AEA算法具有类似退火机制的性质,在行走方向上引入概率,使得算法具有一定的反向爬坡能力,从而跳出局部最优。采用AEA算法进行Kriging模型参数的求解减小了对初值的依赖性,提高了模型的精度。
3 结合单调性和凹凸性先验的Kriging建模对于一个已经确定了模型结构的Kriging模型,训练过程就是相关参数θ的求解过程,使得模型具有较好的预测性能。AEA算法能够在全局范围内搜索到函数的g(θ) 最小值对应的参数θ,这也是理论上的最优参数。然而,有些参数θ′对应的g(θ) 的值稍大一些,但拟合的模型却更贴合原模型,即理论上的最优参数并不一定是最贴近原模型的参数,建模过程中还需要尽可能的利用专家知识构造更贴合实际的模型。
为了解决这一问题,提高Kriging模型的预测能力,利用单调性和凹凸性先验知识,提出验证机理信息的方法和融合机理先验的Kriging建模方法。
3.1 系统采样验证法检验单调性先验和凹凸性先验Kriging模型的输出函数结构较为复杂,一阶、二阶导数的计算难度较大,难以通过求输出函数的一阶二阶导数验证其单调性和凹凸性先验知识信息,必须选择其他方法进行验证。
对于一个单输入单输出系统,若已知输出在区间
采用Pierre Gy[9]提出的系统抽样方法来验证模型的先验知识。系统采样是在相等的距离里采样收集的样本,这在大多数情况下会得到最低的采样方差。
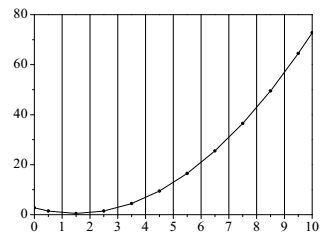
对于单调性先验知识的验证,将验证区间进行若干等分,如图 1所示等分为10份。对每个区间的中点进行采样,产生10个样本点。分别对相邻两个点进行单调性关系验证,如果整个区间都满足先验知识,则认为该模型在该区间是满足约束条件的。例如,若已知图 1中该区间为单调增区间,由于在前两个点上违背了单调先验,违背次数计为2,因此需要在参数优化过程中根据违背程度对目标函数施加惩罚。对于凹凸性先验知识的验证在图 1中每相邻的3个点中进行。同理,如果整个区间都满足先验知识,则认为该模型在该区间是满足约束条件的,否则根据违背程度在参数优化过程中对目标函数施加惩罚。显然,对已知先验信息的一个采样区间,采样次数越多,验证的结果越准确,但智能搜索算法在每一次迭代过程中都需要对样本点进行验证,算法的求解压力也更大,因此在实际应用中可以平衡精度和速度的要求,根据先验区间的长度和位置,有侧重的分配采样点个数。
|
图 1 系统抽样示意图 Fig.1 Diagram of systematic sampling |
设置单调性的违背次数M1,初始值为0,若已知系统输入变量xi在J1i个区间上的单调性先验知识,对于第k个区间[xikL, xikU],固定其他输入变量的值,通过系统采样方法在已知机理信息的区间上取mik个样本点。对于单调性的验证,将每个点与后一个点比较,验证前mik-1个点是否符合单调性先验知识,若违背先验知识,则将计数变量M1的值加一,否则不变。M1的增加值则是这mik-1个检验样本点中违背单调性机理信息的点的数量。其余区间上的先验信息也按此方法验证。对于凹凸性的验证,设置凹凸性违背次数计数变量M2的初始值为0,若已知系统输入变量xi在J2i个区间上的凹凸性先验知识,对于第t个区间[xikL, xikU],固定其他输入变量的值,通过系统采样方法在已知机理信息的区间上取nit个样本点,将每个点与后两个点比较验证前nit-2个点上是否符合凹凸性先验知识,若违背先验知识,则将计数变量M 2的值加一,否则不变。M 2的增加值则是这nit-2个检验样本点中违背单调性机理信息的点的数量。其余区间上的先验信息也按此方法验证。
定义机理信息违背度χ,统计违背次数占检验总次数的比例,其表达式为:
| $\chi =\frac{{{M}_{\text{1}}}+{{M}_{\text{2}}}}{\sum\limits_{i=\text{1}}^{n}{\sum\limits_{k=\text{1}}^{{{J}_{\text{1i}}}}{\left( {{m}_{\text{i}k}}\text{-}1 \right)+\sum\limits_{i=\text{1}}^{n}{\sum\limits_{t=\text{1}}^{{{J}_{\text{2i}}}}{\left( {{n}_{it}}\text{-}2 \right)}}}}}$ | (16) |
如果系统模型完全符合所有机理先验,χ值为0,若所有点都违背机理先验,χ值为1。χ值较小代表模型轻微违反已知的单调性先验和凹凸性先验,χ越大,表示模型违反单调性先验的程度越大。
3.2 融合单调性和凹凸性先验的Kriging建模设定了模型结构后Kriging模型的建模过程可以看作相关性参数函数最小化的优化过程。类似的,将模型先验作为优化问题的约束项,则参数求解过程转化成约束优化问题,如公式 (17) 所示:
| $\begin{align} & \begin{matrix} \min & F(\theta )=\text{g}(\theta )+\eta {{E}_{\theta }} \\ \end{matrix} \\ & \begin{matrix} s.t. & \chi =0 \\ \end{matrix} \\ \end{align}$ | (17) |
其中,F(θ) 为带有N个未知参数的优化算法目标函数,θ是相关性参数,向量形式为 (θ1,θ2,...,θN)。由公式 (4) 可知,在相关函数R中θ可看做每个样本点之间平方差的系数,为了能更好的预测相关函数,使Kriging模型获得相对平缓的输出响应曲线,具有较强的鲁棒性和预测能力,本文在目标函数中增加正则化项
Kriging模型的求解可以看作带约束的优化问题,文中的约束条件为违反程度χ,χ是一个非负数,当它为0时模型完全符合先验知识,越趋近于0表示拟合的模型越接近于实际过程,因此在优化过程中要尽量使χ越小越好,同时必须保证目标函数F(θ) 尽量小。采用惩罚函数法对约束条件进行处理,得到的目标函数为:
| $\begin{matrix} \min & F(\theta )=f(\theta )+\eta {{E}_{\theta }} \\ \end{matrix}+\mu \chi $ | (18) |
其中μ为惩罚系数。
变化后为无约束优化问题,仍用AEA算法求解,建模过程如下:
| 开始 Step1:分析过程对象,获得机理模型; Step2:选择主要变量,采样获得样本; Step3:确定Kriging模型结构; Step4:设置机理信息验证策略,生成检验输入组合点; Step5:对数据进行预处理; Step6:生成AEA算法的初始种群; Step7:对种群的每个个体,通过模型公式和样本点,计算相关性参数函数f (θ);利用相关性参数计算正则化项Eθ;利用模型公式和检测输入计算机理信息违反度χ; Step8:结合正则化系数η和机理惩罚系数μ,计算每个个体的适应度值F (θ); Step9:算法生成新的个体,计算新个体的适应度值,进化策略选择下一代个体及其适应度值。 Step10:判断是否达到迭代上限或满足收敛条件,若满足则转到Step11,否则转入Step9; Step11:参数组合代入模型,模型实施; 结束 |
为了检验本文提出的方法的有效性,选择函数
| 表 1 输入变量x的单调性先验和凹凸性先验 Table 1 Monotonicity and concave-convexity priori for the input variable x |
| 表 2 输入变量y的单调性先验和凹凸性先验 Table 2 Monotonicity and concave-convexity priori for the input variable y |
使用模式搜索法 (PSA) 对该过程进行优化,在无噪声情况下,搜索得到的θ值为[0.77, 0.68]时,预测样本的预测方差为0.012。在增加噪声情况下,搜索得到的θ值为[1.09, 1.35]时,预测样本的预测方差为0.0452。本文还分别采用AEA算法不加先验性知识做为约束条件和增加先验性知识作为约束条件对该模型参数进行优化。为了去除算法搜索的偶然性,算法搜索过程重复10次,统计分析后结果如表 3所示。
| 表 3 无噪声样本和有噪声样本下的模型精度比较 Table 3 Fitting error comparison of the three models with noise-free and noise sample-sets |
观察无噪声时的三种方法的建模效果,发现用PSA搜索参数时对应的结果仍比用AEA算法搜索参数的结果更差一些,而加入机理信息后的AEApr算法结果相比AEA搜索的结果精度又提升了1/5左右;对于有噪声的样本,建模效果仍是AEApr最优而PSA效果最差,由于Kriging模型的无偏估计特性,模型的预测能力受样本点噪声的影响,改进幅度略小于无噪声样本的情况,因此用AEA算法取代PSA算法搜索参数更具有优势,并且在AEA算法参数搜索过程中增加先验知识的验证能够有效提升Kriging模型的预测精度。
综上所述,本文提出的方法能改进Kriging模型的参数寻优算法使模型获得更优的参数,同时综合单调性、凹凸性先验,进一步修正,获得更符合实际过程的参数,使得模型具有较好的泛化性能,预测能力得到了提升,验证了该建模方法的有效性。
5 纳滤膜溶胶平均粒径估计溶胶-凝胶法是大规模制备陶瓷纳滤膜的重要途径,目前最常用的方法是聚合溶胶路线和颗粒溶胶路线[11, 12]。相比于聚合溶胶路线大量使用有机溶剂,以水作为溶剂的颗粒溶胶路线凭借无毒、低挥发、低成本等优点,被更多的应用于规模化生产,且由于小粒径颗粒溶胶制备技术正在不断更新[13~15],颗粒溶胶路线被认为是更具备竞争力的溶胶合成路线。
从颗粒制取ZrO2-TiO2复合纳滤膜的过程中可以发现:粒径分布越集中、平均粒径越小,制备的纳滤膜具有更好渗透与分离性能。溶胶配置实验影响因素包括前驱体摩尔比、水解温度、前驱体浓度、络合剂添加量、甘油添加量、络合时长等,溶胶粒径稳定性能数据获取周期为一个月左右。只改变水解温度、络合剂添加量和甘油添加量,固定前驱体摩尔比为Zr:Ti=4,前驱体与水的摩尔比为1:555,溶胶浓度0.1 mol⋅L-1以及络合时长1 h,获取实验数据,设置水解温度为50~90℃,甘油与前驱体摩尔比0~1.2,前驱体与络合剂摩尔比3~8,通过软测量建模方法预测水解温度、甘油添加量和络合剂添加量在其他情况下的溶胶平均粒径。
通过机理分析以及对数据的分析,得出如表 4所示先验信息。
| 表 4 输入变量的单调性先验和凹凸性先验 Table 4 Monotonicity and concave-convexity priori of the input variables |
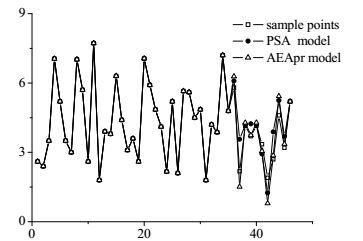
实验样本数据总共46组,随机选择35组作为训练样本,11组作为测试样本。将上述单调性先验和凹凸性先验作为约束条件,建立Kriging模型,使用AEA算法寻求参数。对比PSA方法,样本真实值和模型预测值如图 2。
|
图 2 模型预测值和实际观测值对比 Fig.2 Comparison of observed and predicted outputs |
图 2为PSA和AEApr算法训练与预测样本情况,前35个点为训练效果,后11个点为预测效果。其中,蓝色表示初始样本,红色为PSA方法的训练值和预测值,黑色表示加了机理信息的AEApr算法的训练值和预测值,由于Kriging模型是无偏估计,因此两模型的训练点处预测误差近似为0。不难发现预测点中大多数灰色点相比红色点更接近代表实际值的蓝点。PSA方法的预测均方误差为0.4504,AEApr的预测均方差减小为0.2546,优于PSA优化方法。说明文中提出的方法应用于陶瓷纳滤膜的平均溶胶粒径估计是有效的,可用于其他样本的粒径估计。
6 结论为提升Kriging模型的拟合精度,改进了建模过程中的参数搜索算法。该方法利用对象机理信息和数据样本,采用系统采样法验证模型单调性和凹凸性,充分利用过程机理和样本信息,并将验证信息融入到Kriging建模过程中。通过这一改进可以减少Kriging模型预测精度对选取的参数初值的依赖程度,得到更符合实际过程的预测模型,且对含噪声的样本也具有一定的作用,大大提高了Kriging模型在实际工业过程中的适用性。函数仿真及陶瓷纳滤膜的平均溶胶粒径估计实验表明该方法可以有效的提升Kriging模型的建模精度和预测效果。但本文的方法也有一定的局限性,当输入样本的维度较高时,参数搜索的计算代价和时间成本较高,在之后进一步的研究中,如何在高维输入下提高参数搜索的效率是值得思考探究和改进的方向。
| [1] | Krige D G. A statistical approach to some mine valuation and allied problems on the Witwatersrand[D]. Johannesburg:University of the Witwatersrand, 1951. |
| [2] | Quirante N, Javaloyes J, Caballero J A. Rigorous design of distillation columns using surrogate models based on kriging interpolation[J]. AIChE Journal , 2015, 61(7): 2169-2187. DOI:10.1002/aic.14798. |
| [3] | WANG Xiao-qiang(王晓强), LUO Na(罗娜), YE Zhen-cheng(叶贞成), et al. Differential evolution algorithm based on Kriging and its application in styrene plant optimization(基于Kriging的差分进化算法及其在苯乙烯流程优化中的应用)[J]. Chinese Journal of Chemical Engineering(化工学报) , 2013, 64(12): 4563-4570. |
| [4] | WANG Meng-han(王梦寒), LI Yan-zhao(李雁召), XIA Zhi-zi(夏知姿), et al. Processing parameters optimization of rapid heat cycle molding based on Kriging meta-model and genetic algorithm(基于Kriging模型与遗传算法结合的RHCM成型工艺参数优化)[J]. Chinese Journal of Chemical Engineering(化工学报) , 2014, 65(12): 5054-5060. |
| [5] | Bouhlel M A, Bartoli N. Improving Kriging surrogates of high-dimensional design models by Partial Least Squares dimension reduction[J]. Structural and Multidisciplinary Optimization , 2016, 53(5): 935-952. DOI:10.1007/s00158-015-1395-9. |
| [6] | Haeri A, Javad F M. Efficient reliability analysis of laminated composites using advanced Kriging surrogate model[J]. Composite Structures , 2016, 149: 26-32. DOI:10.1016/j.compstruct.2016.04.013. |
| [7] | Lophaven S N. Aspects of the matlab toolbox DACE[R]. Copenhagen:Technical University of Denmark, 2002. |
| [8] | LI S J, Li F. Alopex-based evolutionary algorithm and its application to reaction kinetic parameter estimation[J]. Computers and Industrial Engineering , 2011, 60(2): 341-348. DOI:10.1016/j.cie.2010.11.018. |
| [9] | Pitard F F. Pierre Gy's sampling theory and sampling practice. Heterogeneity, sampling correctness, and statistical process control[M].Florida: The Chemical Rubber Company Press, 1993. |
| [10] | Svergun D I, Semenyuk A V, Feigin L A. Small-angle-scattering-data treatment by the regularization method[J]. Foundations and Advances , 1988, 44(3): 244-251. |
| [11] | Topuz B, Ciftcioglu M. Sol-gel derived mesoporous and microporous alumina membranes[J]. Journal of Sol-Gel Science and Technology , 2010, 56(3): 287-299. DOI:10.1007/s10971-010-2305-7. |
| [12] | Sakka S. Handbook of sol-gel science and technology:processing, characterization and applications[M].Holland: Kluwer Academic Publishers, 2005. |
| [13] | Chen X F, Zhang W, Lin Y Q, et al. Preparation of high-flux Y-alumina nanofiltration membranes by using a modified sol-gel method[J]. Microporous and Mesoporous Materials , 2015, 214: 195-203. DOI:10.1016/j.micromeso.2015.04.027. |
| [14] | Cai Y Y, Chen X F, Wang Y, et al. Fabrication of palladium-titania nanofiltration membranes via a colloidal sol-gel process[J]. Microporous and Mesoporous Materials , 2015, 201: 202-209. DOI:10.1016/j.micromeso.2014.08.061. |
| [15] | Cai Y Y, Wang Y, Chen X F, et al. Modified colloidal sol-gel process for fabrication of titania nanofiltration membranes with organic additives[J]. Journal of Membrane Science , 2014, 476: 432-441. |




