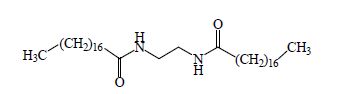
N,N'-乙撑双硬脂酰胺(简称EBS,CAS110-30-5),外观为白色至淡黄色粉状或粒状物,耐酸碱和水介质,常温下不溶于乙醇、丙酮、苯、甘油、四氯化碳等大多数普通溶剂[1]。EBS含有两个长碳链疏水基团和两个极性酰胺基团,所以具有低温抗粘性和高温润滑性,分子结构式如图 1所示。EBS是一种多功能加工助剂,与合成树脂具有良好的相容性,可用于润滑剂、消泡剂、防粘剂、分散剂和成孔剂等,在工业生产中具有非常广泛的应用[2, 3]。虽然EBS用途广泛,文献也有所报道[4],但研究重点一般着重于解决合成工艺路线存在能耗大,反应温度高,产品纯度低等问题,而EBS的热力学和动力学数据仍然十分匮乏,有关热分解过程及动力学方面的研究鲜有报道。本文通过考察在程序升温过程中EBS的TGA-DTA曲线[5],研究它的热分解过程,推导出可能的热分解反应的机理模型,得到热分解反应的动力学方程,为进一步开发与利用EBS提供基础数据。
|
图 1 EBS的分子结构式 Fig.1 Molecular structure of EBS |
FLASH EA 1112型元素分析仪(美国热电公司);FTIR傅里叶红外光谱仪(北京北分瑞利分析仪器公司);WRS-1B数字熔点仪(上海精密科学仪器有限公司);DSC-60差示扫描量热仪(日本岛津公司);SPN-500 型氮气发生器(北京中惠普分析技术研究所);DTG-60热重-差热联用分析仪(日本岛津公司)。
N,N'-乙撑双硬脂酰胺(江西威科油脂化学有限公司);乙醚(天津科密欧化学试剂有限公司);α-Al2O3(TGA标准物质,日本岛津)。
2.2 样品纯化与表征室温下,杂质硬脂酸可溶于乙醚而EBS不溶,所以用乙醚洗涤样品可得高纯度EBS。将8 g样品加入100 mL乙醚中,搅拌30 min,过滤。多次洗涤、干燥至恒重。
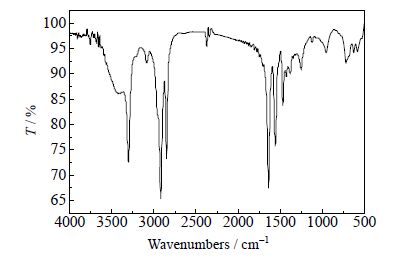
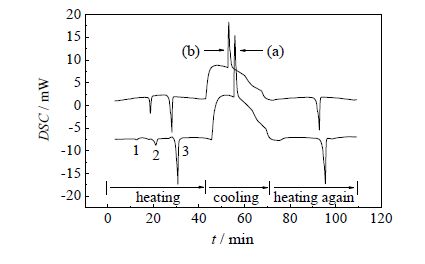
经元素分析仪检测,纯化样品中各元素的质量分数和理论值基本一致,如表 1所示。红外光谱如图 2所示:N-H键3300.61 cm-1(尖峰)、3074.93 cm-1;C=O键1639.04 cm-1;C-N键伸缩振动和N-H键弯曲振动1556.62 cm-1;-CH2和-CH3分别在2918.51和2850.02 cm-1。数字熔点仪测定EBS的熔程为420.35 ~ 420.45 K(文献值[1]418.35 ~419.35 K)。未提纯样品(a)和提纯样品(b)的DSC曲线见图 3,由图 3可知,在第一次加热过程中未提纯样品有三个吸热峰,峰1是硬脂酸的熔融峰;经提纯后的样品在这一加热段仅剩有峰2和峰3,峰1已经消失。一般情况下,大部分固态物质在受热时会发生晶态的变化,会从晶体形态转换为无定形态,而冷却阶段仅发生多相过渡,晶型变化只和冷却速率有关。从图 3冷却段可以看出,在经历了冷却过程之后再重新加热原样品,在第二次加热过程中峰2消失,说明固-固多相存在于样品中,第一次加热过程呈现的峰2和峰3分别对应不同晶型EBS的熔融峰。综上,样品纯度满足实验要求。
| 表 1 EBS的元素分析 Table 1 Elementary analysis results of EBS |
|
图 2 样品的FT-IR谱图 Fig.2 FT-IR spectra of the sample |
|
图 3 未提纯样品(a)和提纯样品(b)的DSC曲线 Fig.3 DSC results of unpurified (a) and purified (b) samples |
用日本岛津DTG-60型热分析仪,在20 mL⋅min−1的氮气气氛下分别以不同升温速率(5、10、12、20 K·min−1)从室温升至773.15 K,用α-Al2O3作参比,测定DTA-TGA曲线(称样3~5 mg)。同样,在理学岛津DSC-60型热分析仪上,用α-Al2O3作参比,测定DSC曲线。
2.4 理论分析根据非等温动力学理论并结合阿伦尼乌斯方程,固体热分解动力学方程为[6~9]:
| $\frac{\text{d}\alpha }{\text{d}t}=\beta \frac{\text{d}T}{\text{d}t}=A{{e}^{\frac{-E}{RT}}}f\left( \alpha \right)\text{or}\frac{\text{d}\alpha }{\text{d}T}=\frac{A}{\beta }{{e}^{\frac{-E}{RT}}}f\left( \alpha \right)$ | (1) |
式中β为升温速率,T为热力学温度,t为反应时间,A为指前因子,E为活化能,R为摩尔气体常数,$f(\alpha )$为动力学函数模型。$\alpha $为失重率,定义为$\alpha =(m{}_{0}-{{m}_{t}})/({{m}_{0}}-{{m}_{f}})$,m0、mf和mt分别为反应起始、终止和时间t时样品的质量。
上式通常为热分解动力学分析的基础,采用不同的数学处理方法,就会得到不同的热分解动力学计算方法。本研究用Flynn-Wall-Ozawa(FWO)、Kissinger和Šatava-Šesták(S-S)法探讨EBS的热分解动力学,求出“动力学三因子”,即E、A和f(α)。
FWO是一种常用的等转化率线性积分法[10~12],如式(2):
| $\lg \beta =\lg \left( \frac{AE}{Rg(\alpha )} \right)-2.315-0.4567\left( \frac{E}{RT} \right)$ | (2) |
g(α)为30种机理函数的积分形式[13, 14] (见表 2)。α一定时,lgβ与1/T呈线性关系,根据斜率可求不同α的活化能Eo。此法的优点是不需预知反应机理,可避免不同反应机理带来的误差,因此可用来检验假设反应机理函数求出的活化能值。
| 表 2 各种机理函数的g(α)形式 Table 2 Mechanism functions of g(α) |
Kissinger法是一种微分处理方法,其公式为[15, 16]:
| $\ln \frac{{{\beta }_{i}}}{T_{\text{pi}}^{2}}=\ln \left( \frac{{{A}_{\text{k}}}R}{{{E}_{\text{k}}}} \right)-\frac{{{E}_{\text{k}}}}{R}\frac{1}{{{T}_{\text{pi}}}}$ | (3) |
式中Tpi表示升温速率为βi时样品的峰温。以ln(βi/T2pi)对1/Tpi进行线性回归,根据斜率(−Ek/R)求活化能Ek,截距ln(AkR/Ek)求指前因子Ak。
S-S法适用于非等温固相热分解动力学研究,方程为:
| $\lg \text{g}(\alpha )=\lg \left( \frac{{{A}_{\text{s}}}{{E}_{\text{s}}}}{R\beta } \right)-2.315-0.4567\left( \frac{{{E}_{\text{s}}}}{RT} \right)$ | (4) |
对于每个固定的β和机理函数g(α),将lgg(α)对1/T作图,根据直线斜率(−0.4567Es/R)和截距(lg(AsEs/(Rβ))−2.315)计算Es和lg(As)。保留满足条件0 < Es < 400 kJ·mol−1的Es及相应的lg(As), 分别和FWO法计算的Eo及Kissinger法计算的lg(Ak)比较,找出同时在|(Es-Eo)/Eo| ≤ 0.22和|(lgAs−lgAk)/lgAk| ≤ 0.30范围内的Es和lg(As),符合上述要求的g(α)是热分解反应机理函数的积分式[17]。
用非等温法求得E和A后,由方程(5)~(7)计算热分解过程的焓变ΔH≠、熵变ΔS≠和吉布斯自由能变ΔG≠[18]。
| $A{{e}^{\left( -\text{ }\frac{E}{RT} \right)}}=\nu {{e}^{\left( -\text{ }\frac{\Delta {{G}^{\ne }}}{RT} \right)}}=\frac{kT}{h}{{e}^{^{\left( -\text{ }\frac{\Delta {{G}^{\ne }}}{RT} \right)}}}$ | (5) |
| $\Delta {{H}^{\ne }}=E-RT$ | (6) |
| $\Delta {{G}^{\ne }}=\Delta {{H}^{\ne }}-T\Delta {{S}^{\ne }}$ | (7) |
式中:v表示爱因斯坦振动频率,k表示玻尔兹曼常量(1.3807×10-23 J×K-1),h表示普朗克常量(6.625×10-34 J×s)。
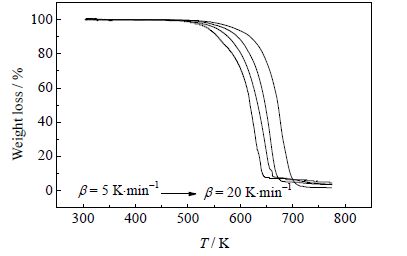
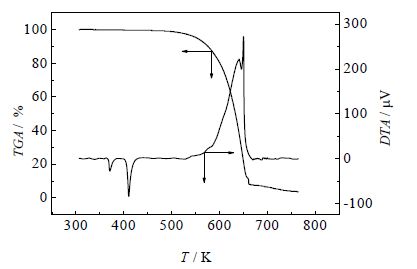
3 数据处理与结果讨论 3.1 热分解EBS的TG曲线如图 4所示,随着升温速率的增加,热分解温度升高,失重率也逐渐增加,TG曲线右移,这表明样品的热分解受升温速率的影响。
|
图 4 氮气氛围下EBS的TG曲线 Fig.4 TG curves of EBS under nitrogen atmosphere |
EBS的DTA-TGA曲线如图 5,在519.15 ~723.15 K内EBS的热分解过程包括两个失重阶段,均伴随放热现象,热分解反应和固体重排可能同时发生。第一阶段(室温~642.15K)平均失重率为61.340%,将这一阶段结束的试样残留物进行红外光谱测试,如图 6。与图 2相比,在3301.72 cm-1 和3429.87 cm-1处出现伯胺基的峰,因此可推断第一阶段的分解产物可能是:C5H11NO、2C和(-CH2)12CH3,其中C5H11NO含有伯胺基、羰基、亚甲基和甲基。当温度升至723.15 K时,平均失重率为96.243%,说明这是一个不完全热分解过程,第二阶段(642.15~723.15 K)平均失重率为34.901%。故第二阶段的分解产物可能为NO、2C和-C5H11,而-C5H11可能进一步分解为小分子气态烃如烷烃或烯烃,反应剩余物为2C。热分解过程如式(8)所示。
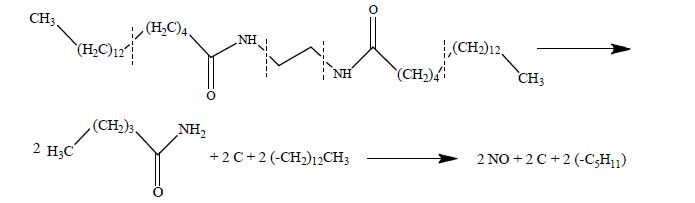
|
(8) |
|
图 5 氮气氛围下EBS的DTA-TGA曲线 Fig.5 DTA-TGA curves of EBS under nitrogen atmosphere |
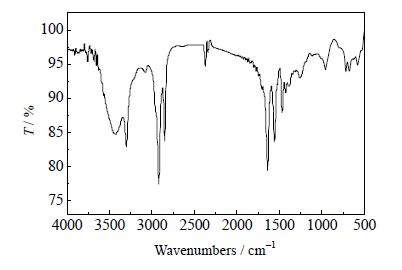
|
图 6 第一阶段分解残留物的FT-IR谱图 Fig.6 FT-IR spectra of the residue from the first stage |
根据FWO法,以lgβ对1/T进行线性回归(如图 7),由直线的斜率和截距可得不同α的Eo(如表 3)。
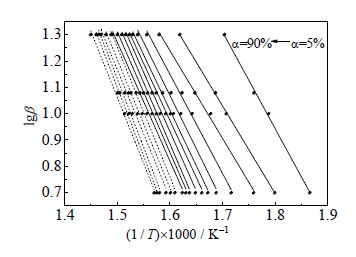
|
图 7 不同转化率下EBS 的FWO 曲线 Fig.7 FWO curves of EBS at different conversion rates |
| 表 3 FWO法计算EBS的活化能Eo Table 3 Activation energy Eo of EBS calculated by FWO method |
根据Kissinger法(如图 8),由直线的斜率和截距得第一失重阶段的Ek和lgAk分别为105.03 kJ·mol-1和8.07 min-1,R2等于0.9943;第二失重阶段的Ek和lgAk分别为112.71kJ·mol-1和8.16 min-1,R2等于0.9988。
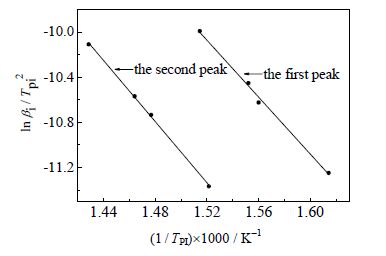
|
图 8 Kissinger法lnβi/Tpi2与1/Tpi的图 Fig.8 Plots of lnβi/Tpi2 against 1/Tpi by Kissinger method |
根据S-S法计算的Es和lgAs如表 4所示。除了第二失重阶段不满足机理函数13、15、16和29之外,第一阶段全部和第二阶段剩余的Es都满足0 <Es< 400 kJ·mol-1。通过比较Eo和Es、lgAk和lgAs(见表 5),对于第一失重阶段,因机理函数19同时符合|(Es-Eo)/Eo| ≤ 0.22和|(lgA-lgAk)/lgAk| ≤ 0.30,且R2大于0.99,所以该段动力学机理为化学反应机理;对于第二失重阶段,机理函数23同时符合上述条件,所以该段动力学机理为成核机理。机理函数分别为g(α) = 1- (1-α)2和g(α) = α,Es分别为71.75 kJ·mol-1和81.54 kJ·mol-1,lg(As)分别为8.41min-1 和9.06 min-1。
| 表 4 S-S法动力学方程的计算结果 Table 4 Calculated kinetic equation results by S-S method |
| 表 5 动力学方程的筛选标准 Table 5 Selection criteria for kinetic equations |
EBS的热分解反应在第一阶段的E和A分别为78.41 kJ·mol-1、2.188×108 min-1,第二阶段分别为88.38 kJ·mol-1和7.586×108 min-1,代入方程(10)~(12)可得平均峰温下的焓变(ΔH≠)、熵变(ΔS≠)和吉布斯自由能变(ΔG≠),结果见表 6所示。
| 表 6 EBS两个分解阶段的热力学参数 Table 6 Thermodynamic parameters of EBS for the two decomposition stages |
通过不同升温速率对EBS进行DSC和TG分析,在519.15~723.15 K热分解过程包括两个阶段。用FWO、Kissinger和S-S法研究了EBS的热分解动力学,第一阶段和第二阶段的活化能和指前因子分别为78.41 kJ·mol-1、2.188×108 min-1和88.38 kJ·mol-1、7.586×108 min-1,热分解机理函数分别为g(α)=1-(1-α)2和g(α)=α。第一阶段的ΔG≠、ΔH≠ 和ΔS≠分别为158.99 kJ·mol-1、73.08 kJ·mol-1和-133.97 J⋅mol-1×K-1,第二阶段分别为167.05 kJ·mol-1、82.73 kJ·mol-1和-124.12 J⋅mol-1×K-1。
符号说明:
| A | — 指前因子,min-1 | v | — 爱因斯坦振动频率 |
| E | — 活化能,kJ⋅mol-1 | α | — 样品失重率,% |
| ΔG≠ | — 吉布斯自由能变,kJ⋅mol-1 | β | — 升温速率,K⋅min-1 |
| ΔH≠ | — 焓变,kJ⋅mol-1 | 下角标 | |
| h | — 普朗克常量,J×s | 0 | — 起始阶段 |
| k | — 玻尔兹曼常量,J×K-1 | f | — 终止阶段 |
| m | — 某时刻样品的质量,mg | k | — Kissinger法求得的热力学参数 |
| R | — 摩尔气体常数 | o | — Flynn-Wall-Ozawa法求得的热力学参数 |
| ΔS≠ | — 熵变,J⋅mol-1×K-1 | p | — 峰顶 |
| T | — 热力学温度,K | s | — Šatava-Šesták法求得的热力学参数 |
| t | — 反应时间,min | t | — 时间 |
| [1] | WU Wen-juan(吴文娟), XU Dong-mei(徐冬梅), ZHANG Ke-da(张可达) . A novel synthesis of ethylene bisstearamide(乙撑双硬脂酰胺的合成)[J]. Petrochemical Technology(石油化工) , 2003, 32 (12) : 1055-1057 |
| [2] | Nazari K A, Nouri A, Hilditch T . The addition of a surfactant at regular time intervals in the mechanical alloying process[J]. Journal of Alloys and Compounds , 2014, 615 : 47-45 DOI:10.1016/j.jallcom.2014.06.142 |
| [3] | Nouri A, Hodgson P D, Wen C E . Effect of process control agent on the porous structure and mechanical properties of a biomedical Ti-Sn-Nb alloy produced by powder metallurgy[J]. Acta Biomaterialia , 2010, 6 (4) : 1630-1639 DOI:10.1016/j.actbio.2009.10.005 |
| [4] | GAO Hua-jing(高华晶), JIN Zhao-hui(金朝辉), ZHOU Bai-ye(周佰业) . Synthesis process and applications of N,N'-ethylene bis stearamide(N,N'-乙撑双硬脂酰胺的合成工艺及应用)[J]. Journal of Jilin Institute of Chemical Technology(吉林化工学院学报) , 2013, 32 (1) : 1-4 |
| [5] | LIU Zhong-ping(刘中平), LÜ Shu-chen(吕书琛), ZHOU Cai-rong(周彩荣) . Thermal decomposition kinetic of inositol(肌醇热分解动力学)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报) , 2013, 27 (3) : 542-546 |
| [6] | Gamlina C D, Dutta N K, Choudhurya N R . Evaluation of kinetic parameters of thermal and oxidative decomposition of base oils by conventional, isothermal and modulated TGA, and pressure DSC[J]. Thermochimica Acta , 2002, 392 : 357-369 |
| [7] | Li X Y, Wu Y Q, Gu D H . Thermal decomposition kinetics of nickel(Ⅱ) and cobalt(Ⅱ) azobarbituric acid complexes[J]. Thermochimica Acta , 2009, 493 (1-2) : 85-89 DOI:10.1016/j.tca.2009.04.010 |
| [8] | Rotaru A, Kropidlowska A, Moanta A . Thermal decomposition kinetics of some aromatic azomonoehters-Part Ⅱ. Non-isothermal study of three liquid crystals in dynamic air atmosphere[J]. Journal of Thermal Analysis and Calorimetry , 2008, 92 (1) : 233-238 DOI:10.1007/s10973-007-8815-z |
| [9] | Wang D J, Fang Z D, Lu L Y . Thermal behavior and non-isothermal kinetics of the polyoxometalate of ciprofloxacin with tungstoposphoric acid[J]. Journal of Wuhan University of Technology , 2007, 22 (2) : 240-244 DOI:10.1007/s11595-005-2240-6 |
| [10] | LU Lin-gang(卢林刚), ZHANG Yan(张燕), YANG Shou-sheng(杨守生) . Thermal decomposition kinetic of novel flame retardant from 1,3,5-tri(5,5-Dibromomethyl-1,3-dioxaphosphorinanyl-2-oxy)benzene(新型阻燃剂1,3,5-三(5,5-二溴甲基-1,3-二氧杂己内磷酰氧基)苯的热分解动力学研究)[J]. Plastics(塑料) , 2009, 38 (1) : 43-45 |
| [11] | Wang Q F, Wang L, Zhang X W . Thermal stability and kinetic of decomposition of nitrated HTPB[J]. Journal Hazardous Materials , 2009, 172 (2-3) : 1659-1664 DOI:10.1016/j.jhazmat.2009.08.040 |
| [12] | XIE Feng-xia(谢凤霞), ZHANG Dan(张丹), ZHANG Xin-xin(张欣欣) . Synthesis, crystal structure and thermal decomposition kinetic of a complex polymer[Cu(py)2(m-bdc)]n(配位聚合物)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报) , 2014, 28 (4) : 695-700 |
| [13] | Huang M X, Lv S C, Zhou C R . Thermal decomposition kinetics of glycine in nitrogen atmosphere[J]. Thermochimica Acta , 2013, 552 : 60-64 DOI:10.1016/j.tca.2012.11.006 |
| [14] | ZHOU Cai-rong(周彩荣), SHI Xiao-hua(石晓华), WANG Hai-feng(王海峰) . Thermal decomposition and the non-isothermal decomposition kinetic of DL-2-naproxen(DL-2-萘普生热分解过程和非等温热分解动力学研究)[J]. Journal of Chemical Engineering of Chinese University(高校化学工程学报) , 2011, 25 (3) : 442-446 |
| [15] | Rotaru A, Moanţa A, Popa G . Thermal decomposition kinetics of some aromatic azomonoethers[J]. Journal of Thermal Analysis and Calorimetry , 2009, 97 (2) : 485-491 DOI:10.1007/s10973-009-0214-1 |
| [16] | ZHU Yuan-jiao(祝远姣), CHEN Xiao-peng(陈晓鹏), ZHOU Long-chang(周龙昌) . Non-isothermal decomposition kinetic of dehydroabieticacid(脱氢枞酸的非等温热分解动力学)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报) , 2009, 23 (3) : 435-439 |
| [17] | Zhang L, Huang M X, Zhou C R . Thermal stability and decomposition kinetics of polysuccinimide[J]. American Journal of Analytical Chemistry , 2013, 4 : 749-755 DOI:10.4236/ajac.2013.412091 |
| [18] | Ma H X, Yan B, Li Z N . Synthesis, molecular structure, non-isothermal decomposition kinetics and adiabatic time to explosion of 3,3-dinitroazetidinium 3,5-dinitrosalicylate[J]. Journal of Thermal Analysis and Calorimetry , 2009, 95 (2) : 437-444 DOI:10.1007/s10973-008-9255-0 |




